Механические колебания и волны
Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Отличительными признаками колебательного движения являются:
- повторяемость движения;
- возвратность движения.
Для существования механических колебаний необходимо:
- наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
- наличие малого трения в системе.
Механические волны – это процесс распространения колебаний в упругой среде.
Содержание
- Виды волн
- Гармонические колебания
- Амплитуда и фаза колебаний
- Период колебаний
- Частота колебаний
- Свободные колебания (математический и пружинный маятники)
- Вынужденные колебания
- Резонанс
- Длина волны
- Звук
- Основные формулы по теме «Механические колебания и волны»
Виды волн
- Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.
Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.
- Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.
Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.
Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.
Гармонические колебания
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:
где ( x ) – координата тела – смещение тела от положения равновесия в данный момент времени; ( A ) – амплитуда колебаний; ( omega t+varphi_0 ) – фаза колебаний; ( omega ) – циклическая частота; ( varphi_0 ) – начальная фаза.
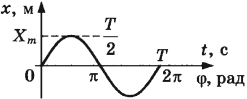
Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.
Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:
где ( v ) – мгновенное значение скорости, т. е. скорость в данный момент времени.
Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:
Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:
где ( a ) – мгновенное значение ускорения, т. е. ускорение в данный момент времени.
Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:
где ( F ) – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.
Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:
где ( W_k ) – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.
Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:
- потенциальная энергия равна нулю;
- кинетическая энергия максимальна.
При максимальном отклонении от положения равновесия:
- кинетическая энергия равна нулю;
- потенциальная энергия максимальна.
Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:
Важно!
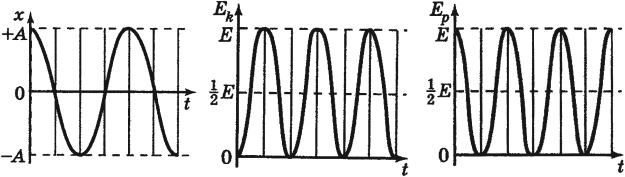
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.
Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).
Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ( A, (X_{max}) ), единицы измерения – м.
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ( varphi ), единицы измерения – рад (радиан).
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
( varphi_0 ) – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Период колебаний
Период колебаний – это время одного полного колебания.
Обозначение – ( T ), единицы измерения – с.
Период гармонических колебаний – постоянная величина.
Частота колебаний
Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ( nu ), единицы времени – с-1 или Гц (Герц).
1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:
Период и частота колебаний – взаимно обратные величины:
Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ( omega ), единицы измерения – рад/с.
Свободные колебания (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
- при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
- силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
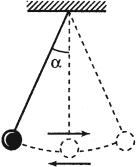
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
Период колебаний математического маятника:
Частота колебаний математического маятника:
Циклическая частота колебаний математического маятника:
Максимальное значение скорости колебаний математического маятника:
Максимальное значение ускорения колебаний математического маятника:
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
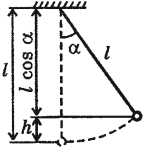
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ( h ), определяется по формуле:
где ( l ) – длина нити, ( alpha ) – угол отклонения от вертикали.
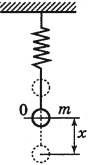
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
Период колебаний пружинного маятника:
Частота колебаний пружинного маятника:
Циклическая частота колебаний пружинного маятника:
Максимальное значение скорости колебаний пружинного маятника:
Максимальное значение ускорения колебаний пружинного маятника:
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.
Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
Резонанс
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
Условие резонанса:
( v_0 ) – собственная частота колебаний маятника.
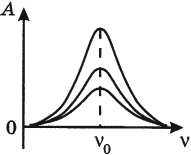
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.
Длина волны
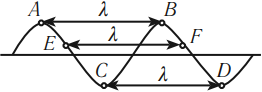
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ( lambda ), единицы измерения – м.
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук (( nu ) < 16 Гц);
- звуковой диапазон (16 Гц < ( nu ) < 20 000 Гц);
- ультразвук (( nu ) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
Скорость звука зависит
- от упругих свойств среды:
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
- от температуры среды:
в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.
Основные формулы по теме «Механические колебания и волны»
Механические колебания и волны
3 (59.24%) 157 votes
Как найти период колебаний и длину волны
Период и частота колебаний являются величинами, обратными по отношению друг к другу. Длина волны связана с частотой через скорость распространения, а циклическая частота — через удвоенное число π.

Инструкция
Все исходные данные переведите в единицы системы СИ: частоту — в герцы (Гц), циклическую частоту — в радианы в секунду (рад/с), период — в секунды, длину волны — в метры.
Чтобы найти период колебаний, зная частоту, возведите ее в степень -1 (или, что то же самое, поделите число 1 на частоту). Если в исходных данных представлена циклическая частота, вначале переведите ее в обычную частоту, для чего поделите на 2π. Если же в условиях дана длина волны, перед вычислением периода найдите по ней частоту, для чего поделите скорость распространения колебаний на длину волны.
Для нахождения длины волны по частоте поделите скорость распространения колебаний на частоту. Если в условиях задачи вместо обычной частоты дана циклическая, вначале переведите ее в обычную, как указано выше. Если дан период, сначала вычислите по нему частоту, возведя его в степень -1.
Скорость распространения электромагнитных колебаний (в т.ч., света) в вакууме равна 299792458 м/с. Чтобы узнать скорость распространения таких колебаний в другой среде, поделите эту константу на коэффициент преломления среды, которая является безразмерной величиной. Поскольку у воздуха этот коэффициент очень близок к единице, при невысоких требованиях к точности скорость света в воздухе можно принять равной скорости света в вакууме. Звук же распространяться в вакууме не может. Его скорость в воздухе составляет 331 м/с, а в воде — 1348 м/с. Обратите внимание: если скорость света с увеличением плотности среды падает, то у звука она при этом, напротив, возрастает.
Вычислив период или длину волны, при необходимости переведите результат в более удобные единицы: период — в миллисекунды, микросекунды, наносекунды, пикосекунды, длину волны — в нанометры, микрометры, миллиметры, сантиметры, километры. Выбор единиц измерения желательно осуществлять таким образом, чтобы не приходилось пользоваться экспоненциальной формой записи чисел.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Основные формулы по физике — КОЛЕБАНИЯ И ВОЛНЫ
При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебани.
Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухани.
Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.
Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна — это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.
Смотрите также основные формулы квантовой физики
Таблица формул: колебания и волны
|
Физические законы, формулы, переменные |
Формулы колебания и волны |
||||
|
Уравнение гармонических колебаний: где х — смещение (отклонение) колеблющейся величины от положения равновесия; А — амплитуда; ω — круговая (циклическая) частота; t — время; α — начальная фаза; (ωt+α ) — фаза. |
|
||||
|
Связь между периодом и круговой частотой: |
|
||||
|
Частота: |
|
||||
|
Связь круговой частоты с частотой: |
|
||||
|
Периоды собственных колебаний 1) пружинного маятника: где k — жесткость пружины; 2) математического маятника: где l — длина маятника, g — ускорение свободного падения; 3) колебательного контура: где L — индуктивность контура, С — емкость конденсатора. |
|||||
|
Частота собственных колебаний: |
|
||||
|
Сложение колебаний одинаковой частоты и направления: 1) амплитуда результирующего колебания где А1 и А2 — амплитуды составляющих колебаний, α1 и α2 — начальные фазы составляющих колебаний; 2) начальная фаза результирующего колебания |
|
||||
|
Уравнение затухающих колебаний: е = 2,71… — основание натуральных логарифмов. |
|
||||
|
Амплитуда затухающих колебаний: где А0 — амплитуда в начальный момент времени; β — коэффициент затухания; t — время. |
|
||||
|
Коэффициент затухания: колеблющегося тела где r — коэффициент сопротивления среды, m — масса тела; колебательного контура где R — активное сопротивление, L — индуктивность контура. |
|
||||
|
Частота затухающих колебаний ω: |
|
||||
|
Период затухающих колебаний Т: |
|
||||
|
Логарифмический декремент затухания: |
|
||||
|
Связь логарифмического декремента χ и коэффициента затухания β: |
|
||||
|
Амплитуда вынужденных колебаний где ω — частота вынужденных колебаний, fо — приведенная амплитуда вынуждающей силы, при механических колебаниях: при электромагнитных колебаниях: |
|
||||
|
Резонансная частота |
|
||||
|
Резонансная амплитуда |
|
||||
|
Полная энергия колебаний: |
|
||||
|
Уравнение плоской волны: где ξ — смещение точек среды с координатой х в момент времени t; k — волновое число: |
|
||||
|
Длина волны: где v скорость распространения колебаний в среде, Т — период колебаний. |
|
||||
|
Связь разности фаз Δφ колебаний двух точек среды с расстоянием Δх между точками среды: |
|
Поделитесь ссылкой с друзьями:
Похожие таблицы
Комментарии:
КОЛЕБАНИЯ И ВОЛНЫ
Колебания
Механические колебания — периодически повторяющиеся изменения положения тела (материальной точки) относительно положения равновесия.
Амплитуда — максимальное отклонение тела от положения равновесия.
Период — время за которое совершается одно полное колебание. Единица измерения секунда (с).
Частота — количество колебаний
в единицу времени
. Измеряется частота в герцах (Гц) показывающих количество колебаний за секунду. К примеру величина 50 Гц говорит нам о том, что система за одну секунду совершила 50 колебаний.
Так как период это время за которое совершается одно полное колебание, можно выразить частоту следующим образом:
Гармонические колебания — колебания происходящие по законам синуса или косинуса (гармоническому закону).
Фаза колебания () — аргумент периодической функции, описывающей колебательный или волновой процесс.
Начальная фаза колебания — значение фазы колебаний в начальный момент времени, т.е. при t = 0.
Циклическая частота — скалярная физическая величина, мера частоты вращательного или колебательного движения. Единица измерения радиан в секунду (рад/с).
Исходя из этого можно записать
Свободные колебания — колебания возникающие за счет внутренних сил системы, после того как она была выведена из состояния равновесия.
Собственные частота колебаний — частота свободных колебаний колебательной системы.
Затухающие колебания — колебания в которых происходит постепенное уменьшение амплитуды в результате действия сил сопротивления движению (силы трения, силы сопротивления воздуха..).
Вынужденные колебания — колебания, происходящие под действием внешних периодически изменяющейся сил.
Резонанс — резкое увеличение амплитуды колебания при совпадении собственной частоты колебательной системы, с частотой вынуждающей силы.
Математический маятник
Математический маятник — механическая колебательная система представляющая из себя материальную точку подвешенную на нерастяжимой невесомой нити в поле силы тяжести.
Формула Гюгенса для определения периода колебаний математического маятника. l — длинна маятника.
Циклическая частота колебаний математического маятника.
Пружинный маятник
Пружинный маятник — механическая колебательная система представляющая из себя пружину жесткостью , с материальной точкой массой
на одном конце этой пружины.
Колебательный контур
Электромагнитные колебания — периодические изменения напряжённости и магнитной индукции.
Колебательный контур — электрическая цепь, состоящая из конденсатора ёмкостью и катушки индуктивностью
. В этой цепи происходят свободные электромагнитные колебания.
Циклическая частота и период собственных колебаний контура определяются по формуле Томсона:
Связь между амплитудными (максимальными) значениями тока в контуре и заряда на конденсаторе:
Энергия контура:
Связь между амплитудными (максимальными) значениями тока и напряжения в контуре (закон сохранения энергии в колебательном контуре):
Переменный ток
Переменный ток — электрический ток периодически меняющий свое направление.
Действующее значение силы переменного тока равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время.
Действующее значение напряжения в цепи переменного тока равно напряжению постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время.
Средняя по времени тепловая мощность переменного тока:
Емкостное сопротивление — сопротивление конденсатора в цепи переменного тока. Емкостное сопротивление зависит от частоты переменного тока, чем частота выше, тем сопротивление ниже. Для постоянного тока конденсатор по сути представляет разрыв цепи, по этому для постоянного тока емкостное сопротивление стремиться к бесконечности.
Где циклическая частота переменного тока.
Закон Ома для участков цепи, содержащих емкость:
Индуктивное сопротивление — сопротивление катушки индуктивности в цепи переменного тока. Так как изменение тока в цепи приводит к появлению токов самоиндукции противодействующих этому изменению, то увеличение частоты переменного тока приводит к увеличению индукционного сопротивления.
Закон Ома для участков цепи, содержащих индуктивность:
Трансформатор
Трансформатор — электромагнитное устройство, которое используется для передачи и преобразования электрической энергии из одной катушки индуктивности на сердечнике в другую. Частота переменного тока при этом не меняется.
Идеальный трансформатор — трансформатор в котором энергетические потери пренебрежимо малы.
Отношение напряжений на вторичной и первичной
обмотках идеального трансформатора равно отношению количеств их витков. (
на вторичной и
первичной). Само это соотношение называют коэффициентом трансформации
.
Если коэффициент трансформации больше единицы, то трансформатор называется понижающим, если меньше, то повышающим.
Закон сохранения энергии для идеального трансформатора:
КПД неидеального трансформатора:
Волны
Волны — колебания распространяющийся в упругих средах. Если направление распространения волн и направление колеблющихся частиц среды совпадают то такие волны называются продольными. А если эти направления перпендикулярны друг другу, то такие волны называют поперечными.
Так как волновые процессы являются часным случаем колебательного движения, они так же будут характеризоваться своими частотой и периодом. Но помимо этого у волн есть еще свои дополнительные характеристики, отличающие их от обычного колебательного движения.
Длина волны — расстояние, на которое успевает распространиться волна за один период;
Скорость распространения волны — отношение длинны волны к периоду ее колебания.
Звуковые волны — разновидность механических волн в слышимом для человека диапазоне ( от 16 Гц до 20 кГц).
Гармонические колебания происходят по
закону:
x
= A
cos(ωt
+ φ0),
где
x
– смещение частицы от положения
равновесия, А
– амплитуда колебаний, ω – круговая
частота, φ0
– начальная фаза, t
– время.
Период
колебаний T
=
.
Скорость колеблющейся частицы:
υ
=
= – A
ω
sin (ωt
+ φ0),
ускорение
a
=
= –
Aω2
cos
(ωt
+ φ0).
Кинетическая энергия частицы, совершающей
колебательное движение: Ek
=
=
sin2(ωt+ φ0).
Потенциальная
энергия:
En
=
cos2(ωt
+ φ0).
Периоды колебаний маятников
– пружинного
T
=
,
где
m
– масса груза, k
– коэффициент жесткости пружины,
– математического
T
=
,
где
l
– длина
подвеса, g
– ускорение свободного падения,
– физического
T
=
,
где
I
– момент
инерции маятника относительно оси,
проходящей через точку подвеса, m
– масса маятника, l
– расстояние от точки подвеса до центра
масс.
Приведенная
длина физического маятника находится
из условия: lnp
=
,
обозначения те
же, что для физического маятника.
При сложении двух
гармонических колебаний одной частоты
и одного направления получается
гармоническое колебание той же частоты
с амплитудой:
A
= A12
+
A22
+
2A1
A2
cos(φ2
–
φ1)
и
начальной
фазой:
φ =
arctg
.
где
А1,
A2
– амплитуды, φ1,
φ2
– начальные фазы складываемых колебаний.
Траектория
результирующего движения при сложении
взаимноперпендикулярных колебаний
одной частоты:
+
–
cos
(φ2
– φ1)
= sin2
(φ2
– φ1).
Затухающие колебания происходят по
закону:
x
= A0
e—
βt
cos(ωt
+ φ0),
где
β – коэффициент затухания, смысл
остальных параметров тот же, что для
гармонических колебаний, А0
– начальная амплитуда. В момент времени
t
амплитуда колебаний:
A
= A0
e
— βt.
Логарифмическим
декрементом затухания называют:
λ
= ln
= βT,
где
Т
– период колебания: T
=
.
Добротностью колебательной системы
называют:
D
=
.
Уравнение плоской бегущей волны имеет
вид:
y
= y0
cos
ω(t
±
),
где
у
– смещение колеблющейся величины от
положения равновесия, у0
– амплитуда, ω – круговая частота, t
– время, х
– координата, вдоль которой распространяется
волна, υ
– скорость распространения волны.
Знак
«+» соответствует волне, распространяющейся
против оси X,
знак «–» соответствует волне,
распространяющейся по оси Х.
Длиной волны называют ее пространственный
период:
λ
= υT,
где
υ–скорость
распространения волны, T–период
распространяющихся колебаний.
Уравнение волны можно записать:
y
= y0
cos
2π
(+
).
Стоячая волна описывается уравнением:
y
= (2y0
cos
)
cos ωt.
В скобки заключена амплитуда стоячей
волны. Точки с максимальной амплитудой
называются пучностями,
xп
= n,
точки с нулевой
амплитудой – узлами,
xу
=
(n
+
)
.
Примеры решения задач
Задача
20
Амплитуда
гармонических колебаний равна 50 мм,
период 4 с и начальная фаза
.
а) Записать уравнение этого колебания;
б) найти смещения колеблющейся точки
от положения равновесия при t=0
и при t
= 1,5 с; в) начертить график этого движения.
Решение
Уравнение
колебания записывается в виде x
= a
cos(t
+
0).
По
условию известен период колебаний.
Через него можно выразить круговую
частоту
=
.
Остальные параметры известны:
а)
x
= 0,05 cos(t
+
).
б)
Смещение x
при t
=
0.
x1
= 0,05 cos=
0,05
=
0,0355 м.
При
t
=
1,5 c
x2
= 0,05 cos(1,5
+
)=
0,05 cos
=
– 0,05 м.
в
график функцииx=0,05cos
(t
+
)
выглядит следующим образом:
Определим
положение нескольких точек. Известны
х1(0)
и х2(1,5),
а также период колебаний. Значит, через
t
= 4 c
значение х
повторяется, а через t
=
2 c
меняет знак. Между максимумом и минимумом
посередине – 0 .
Задача
21
Точка
совершает гармоническое колебание.
Период колебаний 2 с, амплитуда 50 мм,
начальная фаза равна нулю. Найти скорость
точки в момент времени, когда ее смещение
от положения равновесия равно 25 мм.
Решение
1
способ. Записываем уравнение колебания
точки:
x
= 0,05 cos
t,
т.
к.
=
=.
Находим
скорость в момент времени t:
υ
=
= – 0,05
cos
t.
Находим
момент времени, когда смещение равно
0,025 м:
0,025
= 0,05 cos
t1,
отсюда
cos t1
=
,
t1
=
.Подставляем
это значение в выражение для скорости:
υ
= – 0,05
sin
=
–
0,05
=
0,136 м/c.
2
способ. Полная энергия колебательного
движения:
E
=
,
где
а
– амплитуда,
– круговая частота,
m
–
масса
частицы.
В
каждый момент времени она складывается
из потенциальной и кинетической энергии
точки
Ek
=
,
Eп
=
,
но k
= m2,
значит, Eп
=
.
Запишем
закон сохранения энергии:
=
+
,
отсюда
получаем: a22
=
υ
2 +
2x2,
υ
=
=
=
0,136 м/c.
Задача
22
Амплитуда
гармонических колебаний материальной
точки А
= 2 см, полная энергия Е
=
3∙10-7
Дж.
При каком смещении от положения равновесия
на колеблющуюся точку действует сила
F
=
2,25∙10-5
Н?
Решение
Полная
энергия точки, совершающей гармонические
колебания, равна:
E
=
.
(13)
Модуль
упругой силы выражается через смещение
точек от положения равновесия x
следующим образом:
F
= k
x
(14)
В
формулу (13) входят масса m
и круговая частота ,
а в (14) – коэффициент жесткости k.
Но круговая частота связана с m
и k:
2
=
,
отсюда
k
= m2
и F
= m2x.
Выразив m2
из
соотношения (13) получим:
m2
=
,
F
=
x.
Откуда
и получаем выражение для смещения x:
x
=
.
Подстановка
числовых значений дает:
x
=
= 1,5∙10-2
м
= 1,5 см.
Задача
23
Точка
участвует в двух колебаниях с одинаковыми
периодами и начальными фазами. Амплитуды
колебаний А1
=
3 см и А2
= 4 см. Найти амплитуду результирующего
колебания, если: 1) колебания происходят
в одном направлении; 2) колебания взаимно
перпендикулярны.
Решение
-
Если
колебания происходят в одном направлении,
то амплитуда результирующего колебания
определится как:
A
=
,
где
А1
и А2
– амплитуды складываемых колебаний,
1
и 2–начальные
фазы. По условию начальные фазы одинаковы,
значит 2
–
1
=
0, а cos
0 = 1.
Следовательно:
A
=
=
=
А1+А2
=
7 см.
-
Если
колебания взаимно перпендикулярны, то
уравнение результирующего движения
будет:
cos(
2
–
1)
= sin2(
2
–
1).
Так
как по условию 2
–
1
=
0, cos
0 = 1, sin
0 = 0, то уравнение запишется в виде:
=0,
или
=0,
или
.
Полученное
соотношение между x
и у
можно
изобразить на графике. Из графика видно,
что результирующим будет колебание
точки на прямой MN.
Амплитуда этого колебания определится
как:
A
=
=
5 см.
Задача
24
Период
затухающих колебаний Т=4
с, логарифмический декремент затухания
= 1,6 , начальная фаза равна нулю. Смещение
точки при t
=
равно 4,5 см. 1) Написать уравнение этого
колебания; 2) Построить график этого
движения для двух периодов.
Решение
-
Уравнение
затухающих колебаний с нулевой начальной
фазой имеет вид:
x
= A0e
—t
cos2.
Для
подстановки числовых значений не хватает
величин начальной амплитуды А0
и
коэффициента затухания .
Коэффициент
затухания можно определить из соотношения
для логарифмического декремента
затухания:
=
Т.
Таким
образом
=
=
= 0,4 с-1.
Начальную
амплитуду можно определить, подставив
второе условие:
4,5
см
= A0
cos
2= A0
cos
=A0
.
Отсюда
находим:
A0
=
4,5∙
(см)
= 7,75 см.
Окончательно
уравнение движения:
x
= 0,0775
cos
t.
-
Для
построения графика сначала рисуем
огибающую x
=
0,0775
,
а затем колебательную часть.
Задача
25
Чему
равен логарифмический декремент
затухания математического маятника,
если за t
=
1 мин амплитуда колебаний уменьшилась
в два раза? Длина маятника l
=
1 м.
Решение
Логарифмический
декремент затухания можно найти из
соотношения: =
Т,
где
– коэффициент затухания, Т
– период колебаний. Собственная круговая
частота математического маятника:
0
=
= 3,13 с-1.
Коэффициент
затухания колебаний можно определить
из условия:
A0
=
A0
e—t,
t
= ln2
= 0,693 ,
=
= 0,0116c-1.
Поскольку
<< 0,
то
в формуле
=
можно пренебречь
по сравнению с 0
и
период
колебаний определить по формуле:
T
=
= 2c.
Подставляем
и Т
в выражение для логарифмического
декремента затухания и получаем:
=
T
= 0,0116 с-1
∙ 2 с = 0,0232.
Задача
26
Уравнение
незатухающих
колебаний
дано
в виде
x
=
4
sin600
t
см.
Найти
смещение от положения равновесия точки,
находящейся на расстоянии l
= 75 см от источника колебаний, через t
= 0,01 с после начала колебаний. Скорость
распространения колебаний υ
= 300 м/с.
Решение
Запишем
уравнение волны, распространяющейся
от данного источника: x
= 0,04 sin
600 (t
–
).
Находим
фазу волны в данный момент времени в
данном месте:
t
–
= 0,01 –
= 0,0075 ,
600
∙
0,0075
= 4,5
,
sin
4,5
= sin
= 1.
Следовательно,
смещение точки x
= 0,04 м, т.е. на расстоянии l
=75
см от источника в момент времени t
= 0,01 c
смещение точки максимально.
Список литературы
-
Волькенштейн
В.С. Сборник задач по общему курсу
физики. – СПб.: СпецЛит, 2001. -
Савельев
И.В. Сборник вопросов и задач по общей
физике. – М.: Наука, 1998.
35
Соседние файлы в папке FIZIKA
- #
- #
- #
- #
- #
- #
- #




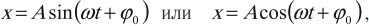
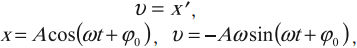
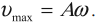
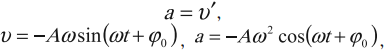
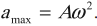
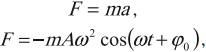
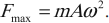
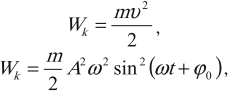
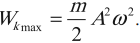
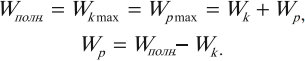
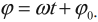




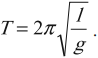
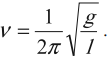
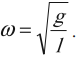
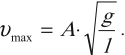
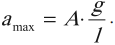
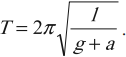
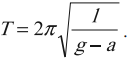
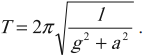
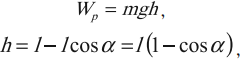
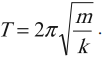
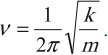
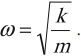
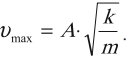
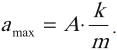
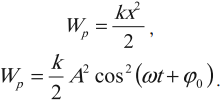
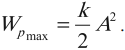
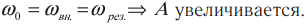
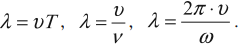
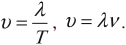



















![Rendered by QuickLaTeX.com [T=2pi sqrt{frac{l}{g}}]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-29425af3eec4256686ccf44fde46b3ca_l3.png)

