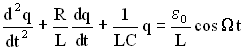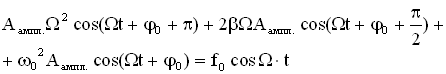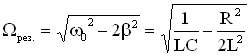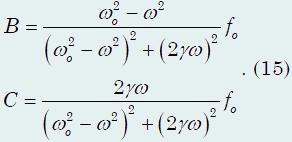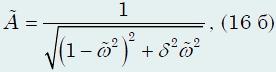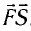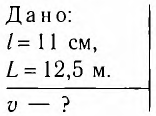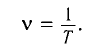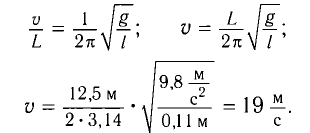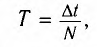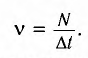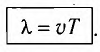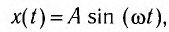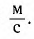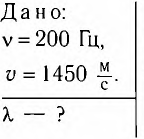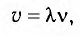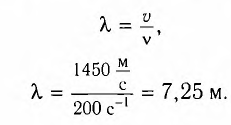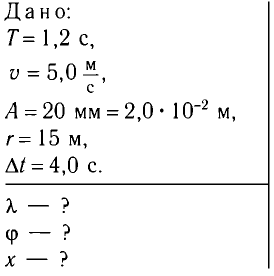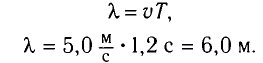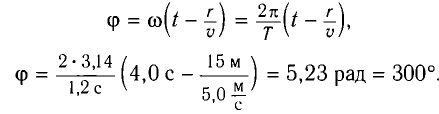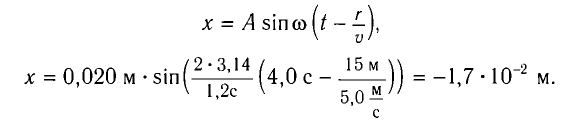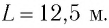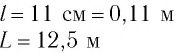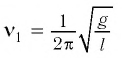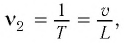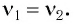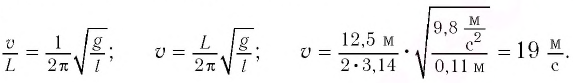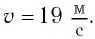Как найти период вынужденных колебаний

4.1. Общие признаки вынужденных механических и электромагнитных колебаний

4.2. Зависимости амплитуды вынужденных колебаний и сдвига фаз от частоты внешнего воздействия. Резонанс

До сих пор мы изучали процессы в механических системах под действием сил, развивающихся в самих системах. Каково будет поведение колебательных систем, к которым тем или иным способом приложена внешняя сила? Для электромагнитного контура аналогичная ситуация возникнет, если в цепь контура включить внешний источник ЭДС.

Рассмотрим явление колебаний, если внешняя (вынуждающая) сила или внешняя ЭДС изменяется в зависимости от времени по гармоническому закону. При этом в системах возникнут колебания, характер которых в той или иной мере повторит характер вынуждающей силы или ЭДС источника. Такие колебания называются вынужденными.

Рассматривая свободные колебания в механической и электромагнитной системах, мы убедились в полной аналогии законов колебаний. Такое же сходство наблюдали для механических и электромагнитных затухающих колебаний. Следует ожидать аналогии законов в механической и электромагнитной системах и при вынужденных колебаниях.

4.1. Общие признаки вынужденных механических и электромагнитных колебаний

1. Рассмотрим вынужденные механические колебаний пружинного маятника, на который действует внешняя (вынуждающая) периодическая сила . Силы, которые действуют на маятник, однажды выведенный из положения равновесия, развиваются в самой колебательной системе. Это сила упругости и сила сопротивления .

Закон движения (второй закон Ньютона) запишется следующим образом: .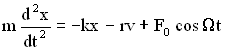

Разделим обе части уравнения на m, учтем, что , и получим дифференциальное уравнение вынужденных колебаний:

.

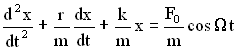
Обозначим (β – коэффициент затухания), (ω₀ – частота незатухающих свободных колебаний), сила, действующая на единицу массы. В этих обозначениях дифференциальное уравнение вынужденных колебаний примет вид:

.

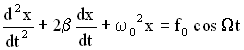
Это дифференциальное уравнение второго порядка с правой частью, отличной от нуля. Решение такого уравнения есть сумма двух решений

.

– общее решение однородного дифференциального уравнения, т.е. дифференциального уравнения без правой части, когда она равна нулю. Такое решение нам известно – это уравнение затухающих колебаний, записанное с точностью до постоянной, значение которой определяется начальными условиями колебательной системы:

, где .

Мы обсуждали ранее, что решение может быть записано через функции синуса.

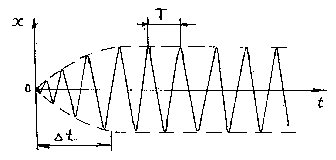
Если рассматривать процесс колебаний маятника через достаточно большой промежуток времени Δt после включения вынуждающей силы (Рисунок 22), то затухающие колебания в системе практически прекратятся. И тогда решением дифференциального уравнения с правой частью будет решение .

Решение — это частное решение неоднородного дифференциального уравнения, т.е. уравнения с правой частью. Из теории дифференциальных уравнений известно, что при правой части, изменяющейся по гармоническому закону, решение будет гармонической функцией (sin или cos) с частотой изменения, соответствующей частоте Ω изменения правой части:

,

где А_ампл. – амплитуда вынужденных колебаний, φ₀ –сдвиг фаз, т.е. разность фаз между фазой вынуждающей силы и фазой вынужденных колебаний. И амплитуда А_ампл., и сдвиг фаз φ₀ зависят от параметров системы (β, ω₀) и от частоты вынуждающей силы Ω.

Период вынужденных колебаний равен . График вынужденных колебаний на Рисунке 4.1.

Рисунок 4.1 – График вынужденных колебаний.

2. Электромагнитные вынужденные колебания.

Электромагнитная система, в которой развиваются вынужденные колебания, — это LCR – контур с включенным в него внешним источником. Рассмотрим случай, когда ЭДС источника изменяется по гармоническому закону:

.

Конденсатор, как рассматривалось ранее, заряжен и при его разрядке в контуре будет идти изменяющийся по времени электрический ток, что вызовет появление в катушке индуктивности ЭДС индукции (). Согласно второму закону Кирхгофа имеем:

,

где U_C, U_R – соответственно падение напряжения на конденсаторе и активном сопротивлении.

Учитывая, что , где I – сила тока в контуре, , где q – величина заряда на одной из обкладок конденсатора, — ЭДС индукции, запишем закон Кирхгофа в виде:

.

Записывая соотношения и , и преобразуя уравнение для закона Кирхгофа, мы получим дифференциальное уравнение вынужденных электромагнитных колебаний в виде:

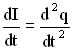
Окончательно дифференциальное уравнений (при использовании обозначений , ) примет вид:

.

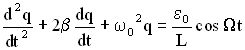
Вид дифференциального уравнения вынужденных электромагнитных колебаний такой же, как и вид дифференциального уравнения для вынужденных колебаний в механической системе. Это дифференциальное уравнение второго порядка с правой частью, поэтому все, что говорилось относительно его решений для механических колебаний верно и для электромагнитной системы. Сначала в системе возникнут и затухающие, и вынужденные колебания, но спустя некоторый промежуток времени, переходный процесс закончится и в системе установятся вынужденные колебаний с той же частотой, что и частота изменения ЭДС источника:

.

φ₀ — сдвиг фаз между изменением заряда конденсатора и действием внешней ЭДС источника.

4.2. Зависимости амплитуды вынужденных колебаний и сдвига фаз от частоты внешнего воздействия. Резонанс

1. Вернемся к механической системе пружинного маятника, на который действует внешняя сила, изменяющаяся по гармоническому закону. Для такой системы дифференциальное уравнение и его решение соответственно имеют вид:

, .

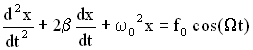
Проанализируем зависимость амплитуды колебаний и сдвига фаз от частоты внешней вынуждающей силы, для этого найдем первую и вторую производную от х и подставим в дифференциальное уравнение.

,

,

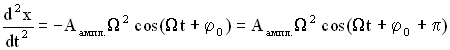
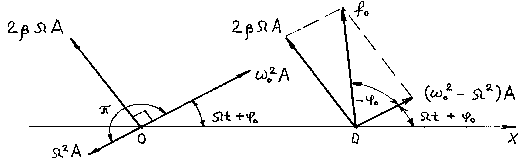
Воспользуемся методом векторной диаграммы. Из уравнения видно, что сумма трех колебаний в левой части уравнения (Рисунок 4.1) должна быть равна колебанию в правой части. Векторная диаграмма выполнена для произвольного момента времени t. Из нее можно определить .

Рисунок 4.1

,

.

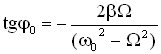
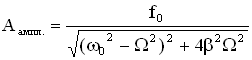
Учитывая значение , ,, получим формулы для φ₀ и А_ампл. механической системы:

,

.

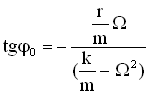
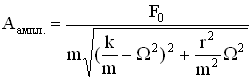
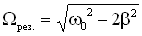
2. Исследуем зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы и величины силы сопротивления в колеблющейся механической системе, по этим данным построим график . Результаты исследования отражены в Рисунке 4.2, по ним видно, что при некоторой частоте вынуждающей силы амплитуда колебаний резко возрастает. И это возрастание тем больше, чем меньше коэффициент затухания β. При амплитуда колебаний становится бесконечно большой .

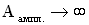
Явление резкого возрастания амплитуды вынужденных колебаний при частоте вынуждающей силы, равной , называется резонансом.

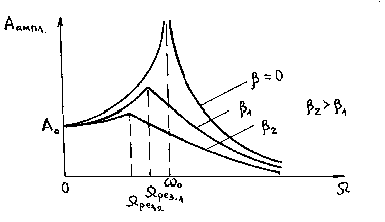
Кривые на Рисунке 4.2 отражают зависимость и называются амплитудными резонансными кривыми.

Рисунок 4.2 – Графики зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы.

3. Используем данные об амплитуде и сдвиге фаз вынужденных колебаний для механической системы и выразим эти же характеристики для аналогичных величин электромагнитной системы (LCR– контур с включенным в его цепь внешним источником ЭДС, величина которой изменяется по гармоническому закону):

,

.

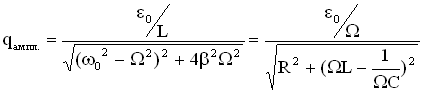
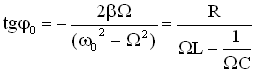
5. Сила тока при установившихся в контуре колебаниях равна:

,

где — амплитуда силы тока, ψ₀ – сдвиг фаз между силой тока и внешнейЭДС в контуре. Амплитуда силы тока и ψ₀ находятся по формулам:

,

, .

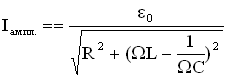
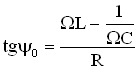
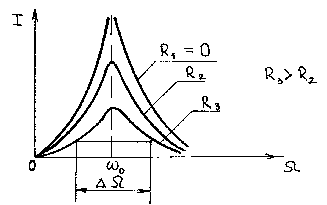
График зависимости представлен на Рисунке 4.3.

Рисунок 4.3

Уравнение вынужденных колебаний и его решение. Резонанс.

Потери
механической энергии в любой колебательной
системе из-за 
наличия сил трения неизбежны, поэтому
без «подкачки» энергии извне колебания
будут затухающими. Существует несколько
принципиально различных способов
создания колебательных систем незатухающих
колебаний. Остановимся более подробно
на рассмотрении незатухающих
колебаний под действием внешней
периодической силы.
Такие колебания называются
вынужденными.
Продолжим изучение
движения гармонического маятника (рис.
6.9 ). 

рис.
6.9

Помимо
рассмотренных ранее сил упругости и
вязкого трения, на шарик действует
внешняя 
вынуждающая
периодическая сила, изменяющаяся по
гармоническому закону

частота,
которой может отличаться от собственной
частоты колебаний маятника ω_o.
Природа
этой сил в данном случае нам не существенна.
Создать такую силу можно различными
способами, например, сообщить шарику
электрический заряд и поместить его во
внешнее переменное электрическое
поле.
Уравнение движения шарика в
рассматриваемом случае имеет вид

Разделим
его на массу шарика и используем прежние
обозначения параметров системы. В
результате получим 
уравнение
вынужденных колебаний:

где
f_o
= F_o/m
− отношение амплитудного значения
внешней вынуждающей силы к массе
шарика.
Общее решение уравнения (3)
достаточно громоздко и, конечно, зависит
от 
начальных условий. Характер движения
шарика, описываемого уравнением (3),
понятен: под действием вынуждающей силы
возникнуть колебания, амплитуда которых
будет возрастать. Этот переходный режим
достаточно сложен и зависит от начальных
условий. По прошествии некоторого
промежутка времени колебательный режим
установится, их амплитуда перестанет
изменяться. Именно установившийся
режим колебаний,
во многих случаях представляет основной
интерес. Мы не будем рассматривать
переход системы к установившемуся
режиму, а сконцентрируем внимание на
описании и изучении характеристик этого
режима.
При такой постановке задачи
нет необходимости задавать начальные 
условия, так как интересующий нас
установившийся режим не зависит от
начальных условий, его характеристики
полностью определяются самим уравнением.
С
аналогичной ситуацией мы сталкивались
при изучении движения тела под действием
постоянной внешней силы и силы вязкого
трения 

По
прошествии некоторого времени тело
движется с постоянной установившейся
скоростью 
v
= F_o/β,
которая не зависит от начальных условий,
и полностью определяется уравнением
движения. Начальные условия определяют
режим, переходный к установившемуся
движению.
На основании здравого смысла
разумно предположить, что в установившемся 
режиме колебаний шарик будет колебаться
с частотой внешней вынуждающей силы.
Поэтому решение уравнения (3) следует
искать в гармонической функции с частотой
вынуждающей силы.
Для начала решим
уравнение (3), пренебрегая силой
сопротивления

 Попробуем
найти его решение в виде гармонической
функции

Для
этого вычислим зависимости скорости и
ускорения тела от времени, как производные
от закона движения 

и
подставим их значения в уравнение (4)

Теперь
можно сократить на 
cosωt.
Следовательно, это выражение обращается
в верное тождество в любой момент
времени, при выполнении условия

Таким
образом, наше предположение о решении
уравнения (4) в виде (5) 
оправдалось: установившийся режим
колебаний описывается функцией

Отметим,
что коэффициент A
согласно полученному выражению (6) может
быть, как положительным (при ω
< ω_o),
так и отрицательным (при ω
> ω_o).
Изменение знака соответствует изменению
фазы колебаний на π
(причина такого изменение будет выяснена
чуть позже), поэтому амплитудой колебаний
является модуль этого коэффициента
|A|.
Амплитуда
установившихся колебаний, как и следовало
ожидать,
пропорциональна
величине вынуждающей силы. Кроме того,
эта амплитуда сложным образом зависит
от частоты вынуждающей силы. Схематический
график этой зависимости показан на рис.
6.10

Рис.
6.10 Резонансная кривая

Как
следует из формулы (6) и хорошо видно на
графике, при приближении 
частоты вынуждающей силы к собственной
частоте системы амплитуда резко
возрастает. Причина такого возрастания
амплитуды понятна: вынуждающая сила
«во время» подталкивает шарик, при
полном совпадении частот установившейся
режим отсутствует − амплитуда возрастает
до бесконечности. Конечно, на практике
такого бесконечного возрастания
наблюдать невозможно: во-первых,
это может привести к разрушению самой
колебательной системы, во-вторых,
при больших амплитудах колебаний нельзя
пренебрегать силами сопротивления
среды.
 Резкое
возрастание амплитуды вынужденных
колебаний при приближении частоты
вынуждающей силы к собственной частоте
колебаний системы называется явлением
резонанса.
Приступим
теперь к поиску решения уравнения
вынужденных колебаний с учетом силы
сопротивления 

Естественно,
что и в этом случае решение следует
искать в виде 
гармонической функции с частотой
вынуждающей силы. Легко заметить, что
поиск решения в форме (5) в данном случае
не приведет к успеху. Действительно,
уравнение (8), в отличие от уравнения
(4), содержит скорость частицы, которая
описывается функцией синуса. Поэтому,
временная часть в уравнении (8) не
сократится. Следовательно, решение
уравнения (8) следует представить в общей
форме гармонической функции

в
которой два параметра A_o
и φ
необходимо найти с помощью уравнения
(8). Параметр A_o
является амплитудой вынужденных
колебаний, φ
− сдвиг фаз между изменяющейся координатой
и переменной вынуждающей силой. Используя
тригонометрическую формулу для косинуса
суммы, функцию (9) можно представить в
эквивалентной форме

которая
также содержит два параметра B
= A_ocosφ
и C
= −A_osinφ,
подлежащих определению. Используя
функцию (10), запишем явные выражения для
зависимостей скорости и ускорения
частицы от времени

и
подставим в уравнение (8):

Перепишем
это выражение в виде 

Для
того чтобы равенство (13) выполнялось в
любой момент времени 
необходимо, чтобы коэффициенты при
косинусе и синусе были равны нулю. На
основании этого условия получаем два
линейных уравнения для определения
параметров функции (10):

Решение
этой системы уравнений имеет вид 

На
основании формулы (10) определяем
характеристики вынужденных колебаний:
амплитуду 

сдвиг
фаз

При
малом затухании эта зависимость имеет
резкий максимум при приближении частоты
вынуждающей силы ω
к собственной частоте системы ω_o.
Таким образом, и в этом случае возможно
возникновения резонанса, поэтому
построенные зависимости часто называют
резонансной кривой. Учет слабого
затухания показывает, что амплитуда не
возрастает до бесконечности, ее
максимальное значение зависит от
коэффициента затухания − с возрастанием
последнего максимальная амплитуда
быстро убывает.
Полученная зависимость
амплитуды колебаний от частоты вынуждающей
силы (16) содержит слишком много независимых
параметров ( f_o,
ω_o,
γ)
для того, чтобы построить полное семейство
резонансных кривых. Как и во многих
случаях, эту зависимость можно существенно
упростить, перейдя к «безразмерным»
переменным. Преобразуем формулу (16) к
следующему виду

и
обозначим

− относительная
частота (отношение частоты вынуждающей
силы к собственной частоте колебаний
системы);

− относительная
амплитуда (отношение амплитуды колебаний
к величине отклонения A_o
= f/ω_o²
при нулевой частоте);

−
безразмерный параметр,
определяющий величину затухания.
Используя эти обозначения, функция (16)
существенно упрощается

так
как содержит всего один параметр −
δ.
Однопараметрическое
семейство резонансных кривых, описываемых
функцией 
(16 б) может быть построено, особенно
легко с помощью компьютера. Результат
такого построения показан на рис. 629.

рис.
6.11

Отметим,
что переход к «обычным» единицам
измерения может быть проведен элементарным
изменением масштаба осей координат. 
Следует
отметить, что частота вынуждающей силы,
при которой амплитуда 
вынужденных колебаний максимальна,
также зависит от коэффициента затухания,
слегка убывая с ростом последнего.
Наконец, подчеркнем, что увеличение
коэффициента затухания приводит к
существенному увеличению ширины
резонансной кривой.
Возникающий сдвиг
фаз между колебаниями точки и вынуждающей
силой также 
зависит от частоты колебаний и коэффициента
их затухания. Более подробно с ролью
этого сдвига фаз мы познакомимся при
рассмотрении преобразования энергии
в процессе вынужденных колебаний.

частота
свободных незатухающих колебаний
совпадает с собственной частотой,
частота затухающих колебаний немного
меньше собственной, а частота вынужденных
колебаний совпадает с частотой вынуждающей
силы, а не собственной частотой.

Вынужденные
электромагнитные колебания

Вынужденными
называются
такие колебания, которые происходят в
колебательной системе под влиянием
внешнего периодического воздействия.

Рис.6.12.
Контур с вынужденными электрическими
колебаниями

Рассмотрим
процессы, протекающие в электрическом
колебательном контуре (рис.6.12),
присоединенном к внешнему источнику,
ЭДС которого изменяется по гармоническому
закону

,

где_m
– амплитуда внешней ЭДС,

 – циклическая
частота ЭДС.

Обозначим
через U_C
напряжение на конденсаторе, а через i
—
силу тока в контуре. В этом контуре кроме
переменной ЭДС (t)
действует еще ЭДС самоиндукции _L
в катушке индуктивности.

ЭДС
самоиндукции прямо пропорциональна
скорости изменения силы тока в контуре

.

Для
вывода дифференциального
уравнения вынужденных колебаний
возникающих
в таком контуре используем второе
правило Кирхгофа

.

Напряжение
на активном сопротивлении R
найдем по закону Ома

.

Cила
электрического тока равна заряду
протекающему за единицу времени через
поперечное сечение проводника

.

Следовательно

.

Напряжение
U_C
на конденсаторе прямо пропорционально
заряду на обкладках конденсатора

.

ЭДС
самоиндукции можно представить через
вторую производную от заряда по времени

.

Подставляя
напряжения и ЭДС во второе правило
Кирхгофа

.

Разделив
обе части этого выражения на L
и распределив слагаемые по степени
убывания порядка производной, получим
дифференциальное уравнение второго
порядка

.

Введем
следующие обозначения и получим

–коэффициент
затухания,

–циклическая
частота собственных колебаний контура.

.
(1)

Уравнение
(1) является неоднородным
линейным дифференциальным уравнением
второго порядка. Такого типа уравнения
описывают поведение широкого класса
колебательных систем (электрических,
механических) под влиянием внешнего
периодического воздействия (внешней
ЭДС или внешней силы).

Общее
решение уравнения (1) складывается из
общего решения q₁
однородного
дифференциального уравнения (2)

(2)

и
любого частного решения q₂
неоднородного
уравнения (1)

.

Вид
общего решения однородного
уравнения
(2) зависит от величины коэффициента
затухания .
Нас будет интересовать случай слабого
затухания 
<< ₀.
При этом общее решение уравнения (2)
имеет вид

,
(3)

где
B
и ₀
– постоянные, задаваемые начальными
условиями.

Решение
(3) описывает затухающие колебания в
контуре. Входящие в (3) величины:

–циклическая
частота затухающих колебаний;

–амплитуда
затухающих колебаний;

–фаза
затухающих колебаний.

Частное
решение уравнения (1) ищем в виде
гармонического колебания, происходящего
с частотой, равной частоте 
внешнего периодического воздействия
– ЭДС, и отстающего по фазе на 
от него

,
(4)

где
– амплитуда вынужденных колебаний,
зависящая от частоты.

Подставим
(4) в (1) и получим тождество

Чтобы
сравнить фазы колебаний, используем
тригонометрические формулы приведения

,

.

Тогда
наше уравнение перепишется в виде

Представим
колебания в левой части полученного
тождества в виде векторной
диаграммы
(рис.6.13)..

Третье
слагаемое, соответствующее колебаниям
на емкости С,
имеющее фазу (t
– )
и амплитуду
,
изобразим горизонтальным вектором,
направленным вправо.

Рис.6.13.
Векторная диаграмма

Первое
слагаемое левой части, соответствующие
колебаниям на индуктивности L,
изобразится на векторной диаграмме
вектором, направленным горизонтально
влево (его амплитуда
).

Второе
слагаемое, соответствующие колебаниям
на сопротивлении R,
изобразим вектором, направленным
вертикально вверх (его амплитуда
),
т. к. его фаза на/2
отстает от фазы первого слагаемого.

Так
как сумма трех колебаний слева от знака
равно дает гармоническое колебание
,
то векторная сумма на диаграмме (диагональ
прямоугольника) изображает колебание
с амплитудойи фазойt,
которая на 
опережает фазу колебаний третьего
слагаемого.

Из
прямоугольного треугольника по теореме
Пифагора можно найти амплитуду A()

(5)

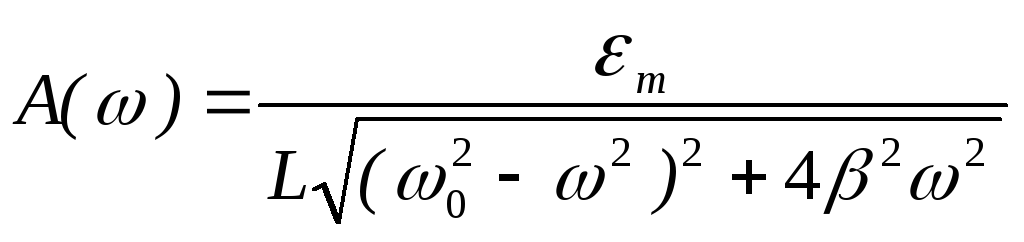
и
tg

как отношение противолежащего катета
к прилежащему катету.

.
(6)

Следовательно,
решение (4) с учетом (5) и (6) примет вид

.
(7)

Общее
решение дифференциального уравнения
(1) является суммой q₁
и q₂

.
(8)

Формула
(8) показывает, что при воздействии на
контур периодической внешней ЭДС в нем
возникают колебания двух частот, т.е.
незатухающие колебания с частотой
внешней ЭДС 
и затухающие колебания с частотой
.
Амплитуда затухающих колебанийсо временем становится пренебрежимо
малой, и в контуре остаются только
вынужденные колебания, амплитуда которых
не зависит от времени. Следовательно,
установившиеся вынужденные колебания
описываются функцией (4). То есть в контуре
возникают вынужденные гармонические
колебания, с частотой, равной частоте
внешнего воздействия, и амплитудой,
зависящей от этой частоты (рис.3а)
по закону (5). При этом по фазе вынужденное
колебание отстает на 
от вынуждающего воздействия.

Продифференцировав
выражение (4) по времени, найдем силу
тока в контуре

_,

где
– амплитуда силы тока.

Запишем
это выражение для силы тока в виде

,
(9)

где
–сдвиг
по фазе между током и внешней ЭДС.

В
соответствии с (6) и рис.2

.
(10)

Из
этой формулы следует, что сдвиг по фазе
между током и внешней ЭДС зависит, при
постоянном сопротивлении R,
от соотношения между частотой вынуждающей
ЭДС 
и собственной частотой контура ₀.

Если

< ₀,
то сдвиг по фазе между током и внешней
ЭДС 
< 0. Колебания силы тока опережают
колебания ЭДС по фазе на угол .

Если

> ₀,
тогда 
> 0. Колебания силы тока отстают от
колебаний ЭДС по фазе на угол .

Если

= ₀
(резонансная
частота),
то 
= 0, т. е. сила тока и ЭДС колеблются в
одинаковой фазе.

Резонанс
– это
явление резкого возрастания амплитуды
колебаний при совпадении частоты
внешней, вынуждающей силы с собственной
частотой колебательной системы.

При
резонансе 
= ₀
и период колебаний

.

Учитывая,
что коэффициент затухания

,

получим
выражения для добротности при резонансе
Т
= Т₀

,

с
другой стороны

.

Амплитуды
напряжений на индуктивности и емкости
при резонансе можно выразить через
добротность контура

,
(15)

.
(16)

Из
(15) и (16) видно, что при 
= ₀,
амплитуда напряжения на конденсаторе
и индуктивности в Q
раз больше амплитуды внешней ЭДС. Это
свойство последовательного RLC
контура используется для выделения
радиосигнала определенной частоты
из спектра радиочастот при перестройке
радиоприемника.

На
практике RLC
контура связаны с другими контурами,
измерительными приборами или усилительными
устройствами, вносящими дополнительное
затухание в RLC
контур. Поэтому реальная величина
добротности нагруженного RLC
контура оказывается ниже величины
добротности, оцениваемой по формуле

.

Реальная
величина добротности может быть оценена
как

Рис.6.14.
Определение добротности по резонансной
кривой

,

где
f
– ширина полосы частот, в которых
амплитуда составляет 0,7 от максимального
значения (рис.4).

Напряжения
на конденсаторе U_C,
на активном сопротивлении U_R
и на катушке индуктивности U_L
достигают максимума при различных
частотах, соответственно

,
,.

Если
затухание мало ₀
>> ,
то все эти частоты практически совпадают
и можно считать что

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Механические колебания.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.

Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний — это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

к оглавлению ▴

Гармонические колебания.

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:

(1)

Выясним смысл входящих в эту формулу величин.

Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.

Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .

Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда

(2)

(3)

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):

.

График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:

.

График гармонических колебаний в этом случае представлен на рис. 2.

Рис. 2. Закон косинуса

Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:

.

График колебаний представлен на рис. 3.

Рис. 3. Закон синуса

к оглавлению ▴

Уравнение гармонических колебаний.

Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:

. (4)

Теперь дифференцируем полученное равенство (4):

. (5)

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :

. (6)

Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:

. (7)

C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.

к оглавлению ▴

Пружинный маятник.

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .

Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

. (8)

Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то . Знаки и всё время противоположны, поэтому закон Гука можно записать так:

Тогда соотношение (8) принимает вид:

или

.

Мы получили уравнение гармонических колебаний вида (6), в котором

.

Циклическая частота колебаний пружинного маятника, таким образом, равна:

. (9)

Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:

. (10)

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).

к оглавлению ▴

Математический маятник.

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.

Запишем для маятника второй закон Ньютона:

,

и спроектируем его на ось :

.

Если маятник занимает положение как на рисунке (т. е. ), то:

.

Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:

.

Итак, при любом положении маятника имеем:

. (11)

Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11):

,

или

.

Это — уравнение гармонических колебаний вида (6), в котором

.

Следовательно, циклическая частота колебаний математического маятника равна:

. (12)

Отсюда период колебаний математического маятника:

. (13)

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

к оглавлению ▴

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

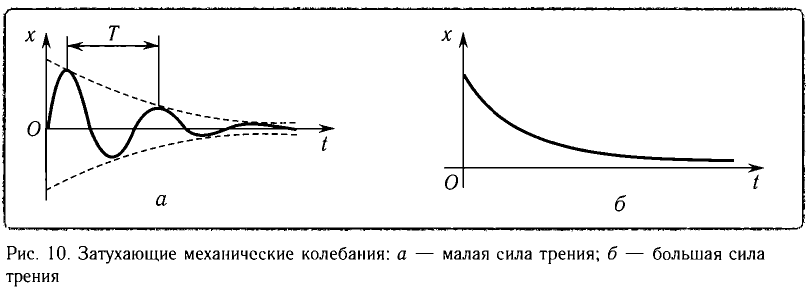
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).

Рис. 6. Затухающие колебания

Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).

Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:

.

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

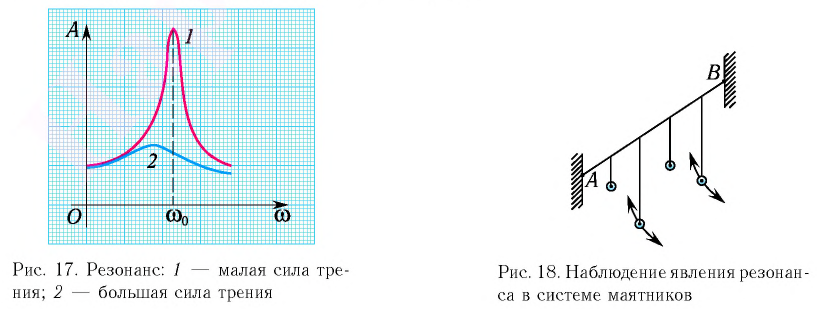
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.

Рис. 7. Резонанс

Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .

Содержание:

Свободные и вынужденные колебания:

Работа силы вычисляется по формуле А =

Как Вам уже известно, механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды его колебаний. Колебания, происходящие с постоянной во времени амплитудой, называются незатухающими колебаниями.

Незатухающие колебания, вызванные кратковременным внешним воздействием, называются свободными или собственными. Они происходят под действием внутренних сил, возникающих в самой системе. Свободные колебания — это колебания, происходящие в отсутствие внешних воздействий на систему, со строго определенной частотой, называемой частотой собственных колебаний системы. Эта частота зависит только от параметров системы. Примерами таких колебаний могут служить колебания математического и пружинного маятников, происходящие в отсутствие сил трения.

В любой реальной системе всегда присутствуют силы трения (сопротивления), поэтому механическая энергия системы с течением времени уменьшается, переходя во внутреннюю энергию. Вместе с тем убыль механической энергии означает и уменьшение амплитуды колебаний.

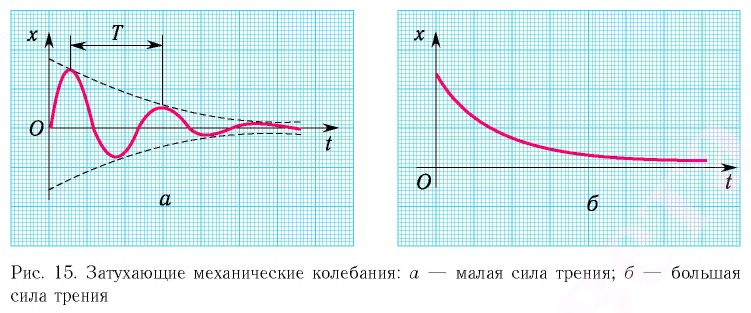
Колебания, амплитуда которых уменьшается с течением времени вследствие потери энергии колебательной системой, называются затухающими колебаниями (рис. 10, а, б).

Уменьшение механической энергии системы (превращение ее во внутреннюю энергию) происходит вследствие трения и сопротивления окружающей среды. Такие системы называют диссипативными (от латинского слова dissipation — рассеяние).

При малых потерях энергии колебания можно считать периодическими и пользоваться такими понятиями, как период и частота колебаний. Так, например, период — промежуток времени между двумя последовательными максимумами колеблющейся физической величины (см. рис. 10, а).

Любые собственные колебания в реальной системе рано или поздно затухают. Чтобы колебания не затухали, необходимо воздействие внешней силы. Однако не всякая внешняя сила заставляет систему двигаться периодически. Например, невозможно раскачать качели, если действовать на них с постоянной по модулю и направлению силой. Внешняя сила тоже должна быть периодической.

Колебания тел под действием внешней периодической силы называются вынужденными, а сила — вынуждающей. В случае гармонической силы 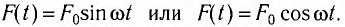. Частота установившихся вынужденных колебаний всегда равна частоте вынуждающей силы.

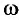
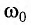
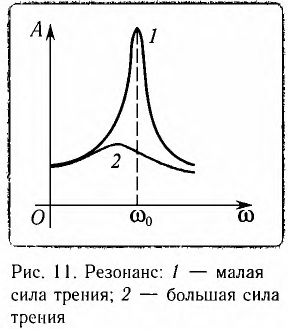
Амплитуда колебаний и энергия, передаваемая системе за период вынужденных колебаний, зависят от того, насколько различаются частота вынуждающей силы и частота собственных колебаний , а также от величины трения в системе.

При вынужденных колебаниях возможно явление, называемое резонансом (от латинского слова resono — откликаюсь, звучу в ответ).

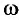
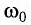
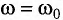
Резонанс — это явление резкого возрастания амплитуды вынужденных колебаний при действии на колебательную систему внешней силы с частотой , совпадающей с собственной частотой системы (() (рис. 11).

При резонансе создаются оптимальные условия для передачи системе энергии от внешнего источника, так как в течение всего периода работа внешней силы над системой положительна. Вспомните процесс раскачивания на качелях — если качели толкать с большой частотой или с малой, то их практически невозможно раскачать. Если же подобрать частоту толчков, близкую к частоте собственных колебаний качелей, то раскачивание будет эффективным.

Пример №1

Определите модуль скорости v движения поезда, при которой маятник длиной l=11 см, подвешенный в вагоне, особенно сильно раскачивается. Длина рельса L = 12,5 м.

Решение

Маятник начинает сильно раскачиваться, когда частота его собственных колебаний совпадает с частотой вынуждающей

Частотой вынуждающей силы является частота ударов колес вагона о стыки рельс. Промежуток времени между двумя последовательными ударами (период)

    (1)

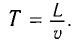
Поскольку частота — величина, обратная периоду, то можно записать частоту вынуждающей силы

Частота собственных колебаний математического маятника

(2)

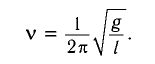
Приравняв формулы (I) и (2), получим

Ответ: о = .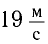

Распространение колебаний в упругой среде. Продольные и поперечные волны

Опыт показывает, что колебания, возбужденные в какой-либо точке упругой среды, с течением времени передаются в ее другие точки. Так от камня, брошенного в спокойную воду озера, кругами расходятся волны, которые со временем достигают берега. Колебания сердца, расположенного внутри грудной клетки, можно ощутить на запястье, что используется для определения пульса.

Перечисленные примеры связаны с явлением распространения механических колебаний в среде.

Механической волной называется процесс распространения колебаний в упругой среде, который сопровождается передачей энергии от одной точки среды к другой.

Механические волны не могут распространяться в вакууме.

Источником механических волн является колеблющееся тело. Если источник колеблется синусоидально, то и волна в упругой среде будет иметь форму синусоиды. Колебания, вызванные в каком-либо месте упругой среды, распространяются в ней с определенной скоростью, зависящей от плотности и упругих свойств среды.

Подчеркнем, что при распространении волны отсутствует перенос вещества, т. е. частицы колеблются вблизи положений равновесия. Среднее смещение частиц относительно положения равновесия за большой промежуток времени равно нулю.

Механизм образования волны можно представить следующим образом. Источник волны — колеблющееся тело — воздействует на частицы упругой среды, соприкасающиеся с ними, и заставляет их совершать вынужденные колебания. Среда вблизи источника деформируется, и в ней возникают силы упругости, препятствующие деформации. Если частицы среды сближаются, то возникают силы отталкивания, а если они удаляются друг от друга, то — силы притяжения. Постепенно эти силы будут действовать на все более удаленные от источника частицы среды, приводя их в колебательное движение, которое будет распространяться в виде волны.

Рассмотрим основные характеристики волны.

Волновой фронт — это воображаемая поверхность, до которой дошло волновое возмущение в данный момент времени.

Линия, проведенная перпендикулярно волновому фронту в направлении распространения волны, называется лучом. Луч указывает направление распространения волны.

Основные характеристики волны:

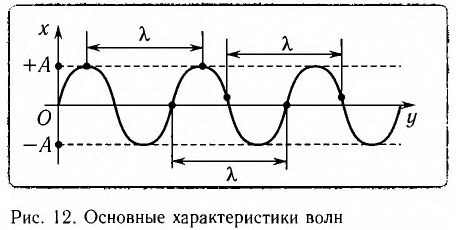
Амплитуда (А) — модуль максимального смещения точек среды из положений равновесия при колебаниях (рис. 12).
 

Период (Т) — время полного колебания (период колебаний точек среды равен периоду колебаний источника волны):

где 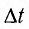— промежуток времени, в течение которого совершаются N колебаний.

Частота (v) — число полных колебаний, совершаемых в данной точке в единицу времени:

Частота волны определяется частотой колебаний источника.

Скорость (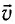) — скорость перемещения гребня волны (это не скорость частиц! ).

Длина волны (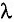) — наименьшее расстояние между двумя точками, колебания в которых происходят в одинаковой фазе, т. е. это расстояние, на которое волна распространяется за промежуток времени, равный периоду колебаний источника (см. рис. 12):

Рассмотрим колебания источника волны, происходящие с циклической частотой 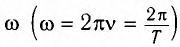и амплитудой А:

где x(t) — смещение источника от положения равновесия.

В некоторую точку среды колебания придут не мгновенно, а через промежуток времени, определяемый скоростью волны и расстоянием от источника до точки наблюдения. Если скорость волны в данной среде равна у, то зависимость от времени t координаты (смещения) х колеблющейся точки, находящейся на расстоянии г от источника, описывается уравнением

    (1)

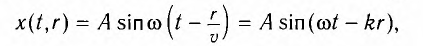
где k — волновое число 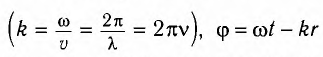— фаза волны.

Выражение (1) называется уравнением распространяющейся (бегущей) волны.

Бегущую волну можно наблюдать при следующем эксперименте: если один конец резинового шнура, лежащего на гладком горизонтальном столе, закрепить и, слегка натянув шнур рукой, привести его второй конец в колебательное движение в направлении, перпендикулярном шнуру, то по нему побежит волна.

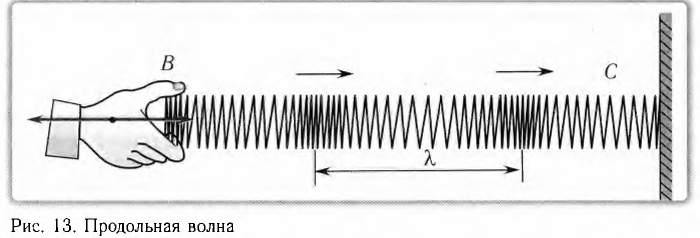
Волна называется продольной, если колебания частиц среды происходят вдоль направления распространения волн. Продольную волну легко получить с помощью длинной пружины, которая лежит на гладкой горизонтальной поверхности и один конец ее закреплен. Упругие волны в газах и жидкостях возникают только при сжатии или разрежении среды. Поэтому в таких средах возможно распространение только продольных волн.

Легким ударом по свободному концу В пружины мы вызовем появление волны (рис. 13). При этом каждый виток пружины будет колебаться вдоль направления распространения волны ВС. Примерами продольных волн являются звуковые волны в газе и жидкости.

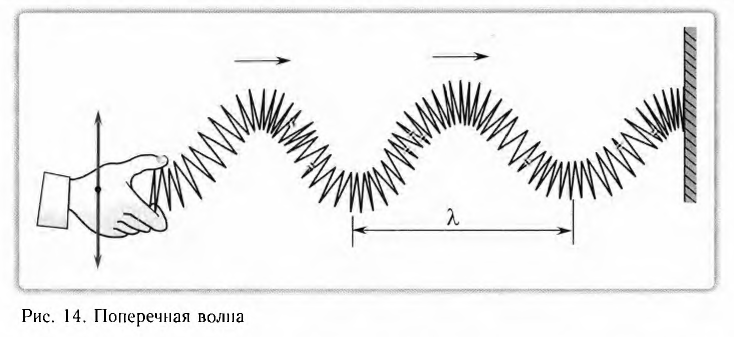
Волна называется поперечной, если частицы среды колеблются в плоскости, перпендикулярной направлению распространения волны. Используя длинную пружину, можно продемонстрировать распространение поперечных волн, если совершать колебания незакрепленного конца перпендикулярно продольной оси пружины (рис. 14). В твердых телах упругие волны могут возникать также и при смещении или сдвиге одних слоев среды относительно других. Поэтому в отличие от жидкостей и газов в твердых телах возможно распространение и поперечных волн.

Поперечные волны вызывают звучание струн музыкальных инструментов при их возбуждении.

Для характеристики энергии, переносимой волнами, используется понятие интенсивности волны (l), определяемое как энергия (W), переносимая волной в единицу времени (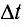= 1с) через поверхность площадью S= I м2, расположенную перпендикулярно к направлению распространения волны:

Другими словами, интенсивность представляет собой мощность, переносимую волнами через поверхность единичной площади, перпендикулярно к направлению распространения волны. Единицей интенсивности в СИ является
ватт на метр в квадрате ().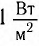

Волны могут распространяться не только в среде, но и вдоль границы раздела двух сред. Такие волны получили название поверхностных волн. Примером данного типа волн служат хорошо знакомые всем волны на поверхности воды.

Пример №2

Определите длину X волны, излучаемой источником колебаний с частотой v = 200 Гц, если модуль скорости распространения волны v = 1450 

Решение

Модуль скорости распространения волны можно вычислить по формуле

где 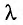— длина волны, v — частота колебаний. Откуда находим

Ответ: 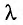= 7,25 м.
 

Пример №3

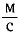
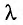
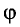
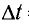
Поперечная волна распространяется вдоль упругого шнура со скоростью, модуль которой v = 5,0/ Период колебания точек шнура Т= 1,2 с, амплитуда колебаний A = 20 мм. Определите длину волны , фазу колебаний и смещение х точки, находящейся на расстоянии г= 15 м от источника колебаний, через промежуток времени = 4,0 с.

Решение

Длина волны находится из выражения

Волна пройдет расстояние г за время 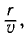 следовательно, фаза колебаний определится по формуле

Подставив вычисленное значение фазы в уравнение колебаний, получим:

Ответ: 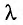= 6,0 м,  = 300°, х = -1,7 см.

Определение свободных и вынужденных колебаний

Силы взаимодействия тел системы называют внутренними. Тела, не входящие в систему, называют внешними телами. Силы, которые действуют на тела системы со стороны внешних тел, называют внешними силами.

Как вам уже известно, механическая энергия гармонического осциллятора (например, груза на пружине) пропорциональна квадрату амплитуды его колебаний. Колебания, происходящие с постоянной во времени амплитудой, называются незатухающими колебаниями.

Колебания, которые совершает система около положения устойчивого равновесия под действием внутренних сил после того, как она была выведена из состояния равновесия и предоставлена самой себе, называются свободными (собственными) колебаниями.

Свободные колебания происходят со строго определенной частотой 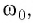 называемой частотой свободных (собственных) колебаний системы. Эта частота зависит только от параметров системы. Примерами таких колебаний могут служить колебания математического и пружинного маятников, происходящие в отсутствие сил трения. Амплитуда свободных колебаний определяется начальными условиями, т. е. тем начальным отклонением или толчком, которым маятник или груз на пружине приведен в движение. Свободные колебания являются самым простым видом колебаний.

В любой реальной колебательной системе всегда присутствуют силы трения (сопротивления), поэтому механическая энергия системы с течением времени уменьшается, переходя во внутреннюю энергию. Вместе с тем убыль механической энергии означает и уменьшение амплитуды колебаний.

Колебания, амплитуда которых уменьшается с течением времени вследствие потери энергии колебательной системой, называются затухающими колебаниями (рис. 15). Уменьшение механической энергии системы (превращение ее во внутреннюю энергию) происходит вследствие трения и сопротивления окружающей среды.

 Систему называют диссипативной (от лат. dissipation — рассеяние), если ее механическая энергия с течением времени уменьшается за счет превращения ее во внутреннюю энергию.

При малых потерях энергии колебания можно считать периодическими и пользоваться такими понятиями, как период и частота колебаний. Так, например, период — промежуток времени между двумя последовательными максимумами колеблющейся физической величины (см. рис. 15, а).

Колебания в любой реальной системе рано или поздно затухают. Чтобы колебания не затухали, необходимо воздействие внешней силы. Однако не всякая внешняя сила заставляет систему двигаться периодически. Например, невозможно раскачать качели, если действовать на них постоянной силой. Внешняя сила тоже должна быть периодической.

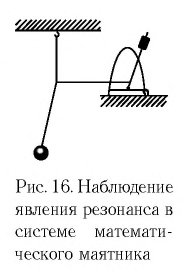
Проведем следующий эксперимент. Соединим математический маятник с метрономом (рис. 16). Изменяя частоту колебаний маятника метронома, добиваемся увеличения амплитуды колебаний математического маятника. Оказывается, что его амплитуда будет максимальной при совпадении собственной частота колебаний маятника и маятника метронома.

Колебания тел под действием внешней периодической силы называются вынужденными, а сила — вынуждающей. В случае гармонической силы: 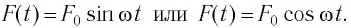 Вначале действия внешней силы наблюдается достаточно сложное движение тела. Спустя некоторое время после начала действия внешней силы колебания приобретают стационарный характер и не зависят от начальных условий. Таким образом, при вынужденных колебаниях система полностью «забывает» свое начальное состояние. Частота установившихся вынужденных колебаний всегда равна частоте вынуждающей силы.

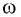
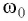
Амплитуда колебаний и энергия, передаваемая системе за период вынужденных колебаний, зависят от того, насколько различаются частота  вынуждающей силы и частота  собственных колебаний, а также от величины трения в системе.

При вынужденных колебаниях возможно явление, называемое резонансом (от лат. resono — откликаюсь, звучу в ответ).

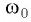
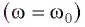
Резонанс — это явление резкого возрастания амплитуды вынужденных колебаний при действии на колебательную систему внешней силы с частотой со, совпадающей с собственной частотой  системы  (рис. 17).

Подвесим на упругой нити 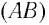 четыре математических маятника с одинаковыми грузами, три из которых имеют различную длину, а длина четвертого равна длине второго (рис. 18). Сначала посмотрим, что будет с маятниками, если раскачать первый или третий маятник. Наблюдения показывают, что через некоторое время начнут качаться и остальные маятники. Но амплитуда их колебаний мала, и вскоре колебания затухают. А вот если раскачать второй маятник, то амплитуда колебаний четвертого будет непрерывно возрастать, пока не достигнет наибольшего значения.

Это происходит потому, что частота собственных колебаний четвертого маятника совпадает с частотой колебаний внешней силы (частотой колебаний второго маятника), так как их длины равны. А колебания первого и третьего маятников, как и в первом эксперименте, быстро затухают.

При резонансе создаются оптимальные условия для передачи системе энергии от внешнего источника, так как в течение всего периода работа внешней силы над системой положительна. Вспомните процесс раскачивания на качелях: если качели толкать очень быстро или очень медленно, их практически невозможно будет раскачать. Если же подбирать частоту толчков, близкую к частоте собственных колебаний качелей, то раскачивание будет эффективным.

Большинство сооружений и машин, обладая определенной упругостью, способны совершать свободные колебания. Поэтому при внешних периодических воздействиях в них вследствие явления резонанса могут возбуждаться колебания большой амплитуды, которые могут привести к разрушительным последствиям. Например, для исключения разрушения мостов вследствие явления резонанса при прохождении по ним войсковых частей приказывают идти вольным шагом (не в ногу). Поезда переезжают мосты либо очень медленно, либо с максимальной скоростью.

В 1750 г. цепной мост вблизи г. Анжер (Франция) был разрушен в результате резонанса, во время прохождения по нему отряда солдат, так как частота их шага совпала с частотой свободных колебаний моста.

В 1906 г. в г. Петербурге (Россия) обрушился Египетский мост, по которому проходил кавалерийский эскадрон.

7 ноября 1940 г. сильный порыв ветра вызвал резонансные колебания Такомского моста (США), что привело к его разрушению.

Пример №4

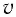
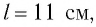
Определите модуль скорости  движения поезда, при которой математический маятник, подвешенный в вагоне, особенно сильно раскачивается. Длина маятника  длина рельса 

Дано:

Решение

Маятник начинает сильно раскачиваться, когда частота его собственных колебаний

совпадает с частотой вынуждающей силы

которая совпадает с частотой ударов колес вагона о стыки рельсов: 
Отсюда

Ответ: