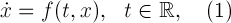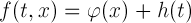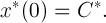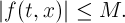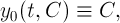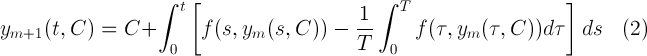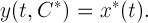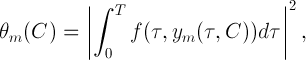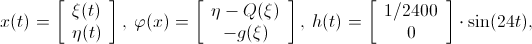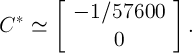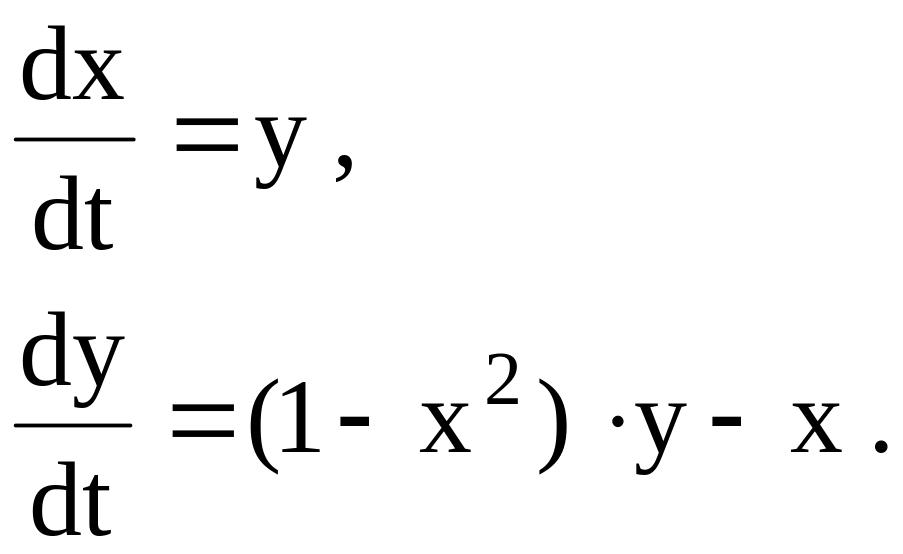Как найти периодическое решение

Нахождение периодических решений дифференциальных уравнений

Пусть дано линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами

где — функция, периодическая с периодом , разлагающаяся в ряд Фурье

Периодическое решение уравнения (47) ищем в виде

Подставляем ряд (49) в уравнение (47) и подбираем его коэффициенты так, чтобы равенство (47) удовлетворялось формально. Приравнивая свободные члены и коэффициенты при и в левых и правых частях полученного равенства, найдем

Первое из равенств (50) дает необходимое условие существования решения вида (49): если , то необходимо, чтобы . Подставляя (50) в (49), получаем

Когда и , где , периодическое решение будет существовать только при условии

Коэффициенты и при расходятся по формулам (50), а коэффициенты и остаются произвольными, так как выражение является общим решением соответствующего однородного уравнения.

В случае невыполнения условий (52) уравнение (47) периодических решений не имеет (возникает резонанс). При и коэффициент остается неопределенным и уравнение (47) имеет бесконечное множество периодических решений, отличающихся друг от друга постоянным слагаемым.

Если правая часть уравнения (47) имеет период , то надо разлагать по периоду и искать решение уравнения (47) в виде

Формулы (50) при этом соответственно изменятся.

---

Пример 8. Найти периодические решения уравнения .

Решение. Имеем . Функция не содержит резонирующего члена , значит, уравнение имеет периодические решения, притом бесконечное множество. По формулам (50) находим коэффициенты

Все периодические решения даются формулой

где и — произвольные постоянные.

---

Пример 9. Найти периодические решения уравнения .

Решение. В данном случае . Проверим выполнимость условий (52). Имеем

Условия (6) существования периодического решения не выполняются. Следовательно, данное уравнение периодических решений не имеет. В самом деле, общее решение уравнения есть

которое, очевидно, не является периодическим из-за наличия слагаемого .

---

Пример 10. Найти периодическое решение уравнения .

Решение. Функция — периодическая с периодом . Разлагаем ее в ряд Фурье в интервале :

Решение данного уравнения ищем в виде

Имеем

Формулы (50) дают

Следовательно, уравнение имеет периодическое решение вида

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Асимптотические методы решения дифференциальных уравнений

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Асимптотические методы позволяют отыскивать приближенные решения дифференциальных уравнений (или систем), близких к таким уравнениям (или системам), решения которых известны. В прикладных задачах часто бывает, что на течение рассматриваемого физического процесса влияют как основные факторы, определяющие ход процесса, так и другие факторы, оказывающие меньшее влияние и меняющие количественные характеристики процесса.

При учете только основных факторов можно получить точное решение системы уравнений, а при учете всех известных факторов система становится сложной и не решается. В таких случаях асимптотические методы часто позволяют найти решение с нужной точностью. Разложение решения по степеням малого параметра — один из наиболее употребительных асимптотических методов.

Следствие теоремы 2. Пусть при (t,x) выполнены условия теоремы 2, и при решение задачи (1) проходит в области D; t0 £ [tl9t2]- Тогда решение x(t, р) задачи (1) при t разлагается по формуле Тейлора по степеням параметра ц до цт включительно: Асимптотические методы решения дифференциальных уравнений Здесь х(Ь9ц) и v^t) — n-мерные вектор-функции, v0(t) = 0) есть решение системы (1) при i = 0, оно считается известным.

Чтобы найти надо подставить разложение (12) в систему (1) и начальные условия, и разложить правые части по степеням /х до /хт включительно. Далее надо приравнять коэффициенты при одинаковых степенях /х. Получается для vx. 9vm система дифференциальных уравнений с начальными условиями. Последовательно решая уравнения системы и пользуясь начальными условиями, находим . vm(£). Пример 2. Найти разложение решения задачи по степеням параметра /х до /х2 включительно.

Решение примера. Правая часть уравнения в области х > 0 име- ет производные любого порядка по ж,/х. Условия теоремы 2 выполнены для любого т, пока решение задачи (13) с l = О проходит в области х > 0. При = 0 задача (13) принимает вид dx/dt = t/x, 1, и имеет решение ж(*) = t, оно проходит в области х > 0 при t > 0. Поэтому v0(*) = t (t > 0).

Разложение х = t + /iv1 +/i2v2 + о(/л2) подставляем в уравнение и начальные условия (13), члены порядка o(/i2) не пишем. Разлагаем дробь в (14) по степеням /х, члены с цк, к > 2, не пишем. Подставляем это в (14) и приравниваем коэффициенты слева и справа при одинаковых степенях параметра /х: при v = -^-2t М0 = 4; (16> при Ц = + «2(l) = i (17) Здесь начальные условия получены из (15). Все дифференциаль- ные уравнения для v<9. vm всегда линейные. Из (16) получаем Vj = — у.

Возможно вам будут полезны данные страницы:

Подставляя это в (17), находим v2 = + fj. Итак, Так как условия теоремы 2 выполнены для любого m ^ 2, то следующий член разложения имеет вид p3v3(t) и, не находя vy в (18) вместо o(/i2) можно написать 0(fi3). Задачи для упражнений: [ | 3« | Отыскание периодических решений. Нижеследующие лемма 2 и теорема 3 дают условия существования периодических решений соответственно для линейной системы с периодической правой частью и для нелинейной системы, близкой к линейной, и указывают методы отыскания таких решений.

Лемма:

Пусть при 0 вектор-функция x(t) — решение уравнения х’ = f(t, х), где вектор-функция f и все dfjdxj непрерывный f(t+p, х) = f(t, х). Если х(р) = ж(0), то решение x(t) продолжается на интервал (-оо, оо) с периодом р. Доказательство. Так как Асимптотические методы решения дифференциальных уравнений то продолженная с периодом р функция x(t) 6 С1.

Она всюду удовлетворяет данному уравнению, ибо для любого k € Z имеем Лемма 2. Если для всех собственных значений матрицы А имеем то система х1 = Ах + f(t) для каждой непрерывной функции f(t) с периодом р имеет (и только одно) решение с периодом р. Условие (19) называется условием отсутствия резонанса. Доказательство. Пусть v(£) — частное решение данной системы с v(0) = 0. В силу теоремы 5 § 9 и следствия 1 § 15 общее решение имеет вид х = etAb + v(t), где Ь — произвольный вектор из Rn.

Чтобы это решение имело период р, по лемме 1 надо, чтобы х(р) = ж(0). То есть Это — линейная алгебраическая система относительно неизвестных координат вектора Ь. Для существования единственного решения достаточно, чтобы det (ерА — 1 • Е) Ф 0, то есть чтобы матрица не имела собственных значений, равных 1. Если АР. АП — собственные значения матрицы А> то согласно замечанию в имеет собственные значения Для А = а + /3i имеем = е?» (cos р/3 + tsinp/5). Это число равно 1 только в случае а = 0, рр = 2*кку к = 0,±1,±2.

Поэтому при условии (19) имеем Теорема 3. Пусть функции f(t), g(t9 х, р) непрерывны при имеют период , где т ^ 1. Пусть выполнено условие (19) и решение x°(t) с периодом р уравнения х Ах + f(t) содержится в области D. Тогда при всех достаточно малых |/*| система имеет решение периода р по t, стремящееся Такое решение единственно и принадлежит классу Ст по ц. -7- Доказательство.

Пусть х(ЬЪ,ц) — решение системы (20) с начальным условием ж(0; ц) = Ь. По лемме 1 оно будет иметь период р, если Докажем, что при малых l существует Ь € R», удовлетворяющее уравнению (21). Функция ж(р;Ь, ц) Е Ст по b, i в силу теоремы 2. При /х = 0 уравнение (20) линейное, как в лемме 2, уравнение (21) принимает вид и имеет единственное решение Ь. Далее, якобиан левой части равенства (21) по координатам Ъ<9. Ьп вектора b при /х = 0 совпадает с детерминантом (22), значит, не равен нулю.

Тогда по теореме о неявных функциях уравнение (21) при достаточно малых имеет решение Ь = Ь(ц), стремящееся к Ь° при такое решение единственно и Ъ(ц) 6 Ст.

Пусть дано уравнение с постоянными коэффициентами а,- и непрерывными функциями /, д периода р по t и д € Ст по у, /1, а корни А характеристического уравнения удовлетворяют условию (19). Тогда для отыскания решения периода р не нужно переходить от уравнения (24) к системе, можно сразу отыскать решение в виде (12), где теперь v^t) — скалярные функции с периодом р. 1 Пример 3. Найти с точностью о(ц2) периодическое решение 1 | уравнения [ Решение примера.

Здесь р = 2т, А2 + 3 = О, Л = ±iV3 Ф 2*ki/p = ki (к Е Z), условие (19) выполнено. Ищем периодическое решение в виде х = v0 + /avx + p2v2 + . Подставляя в уравнение (25) и приравнивая коэффициенты при одинаковых степенях /*, получаем систему уравнений . Надо найти решения t;0, Vj, v2 с периодом 2т. Для каждого из этих уравнений надо найти лишь частное решение (методой неопределенных коэффициентов), так как по теореме 3 при выполнении условия (19) решение с периодом р единственно.

Замена х = а?0 + ру дает . Так как F(x°) = 0, то по формуле Тейлора Остаточный член г Е С (ибо другие члены в равенстве принадлежат Cm+1), г = ц2д(у, ц). Получаем систему вида (20) Если собственные значения матрицы А удовлетворяют условию (19) (нет резонанса), то по теореме 3 система (27) при достаточно малых |/*| имеет решение с периодом р. I Пример 4. Рассмотрим уравнение Решение примера. При i = 0 положения равновесия х< = 1 и х2 = -1.

Периодическое решение

Найдем периодическое решение, близкое к х = 1, Замена х = 1 + /ху Дает Здесь р = 2х, А = -1 ± i Ф 2*ki/p (к € Z), условие (19) выполнено. Поэтому при малых ц уравнение (29) имеет решение периода 2тг и вида у = v0($) + fivx(t) +..где все имеют период 2т. Подставляя это в (29), получаем, как в примере 3, Асимптотические методы решения дифференциальных уравнений Отсюда находим . Следовательно, Уравнение (28) при малых ц имеет и другое решение с периодом 2х.

Оно близко к неустойчивому положению равновесия х2 = -1 и отыскивается аналогичным способом. Можно доказать, что оно неустойчиво. ч Задачи для упражнений: [12], § 18, № 1079-1083. | 5« | Естественно возникает вопрос, в каких случаях разложения по степеням параметра /х, полученные в следствиях теорем 2 и 3, можно продолжить до бесконечного ряда Тейлора, сходящегося к искомому решению при малых /1.

Этот вопрос решается с помощью теоремы

Пуанкаре об аналитической зависимости решения от параметра, см. [13], гл. 1, §6, теорема 1.3 и [2], гл.6, §2, теорема 6.2.1′ и §3, п. 1. I О методах исследования устойчивости периодических решений, получаемых методом малого параметра, см. [2], гл. 7, § 3 и [33], гл. 3, § 10-15. В частности, при условиях теоремы 3 асимптотическая устойчивость периодического решения при достаточно малых обеспечена, если для матрицы А все собственные значения А.

Имеют Re At. а неустойчивость — если есть хотя бы одно Re At. > 0. Поэтому в примере 4 при малых /1 решение (30) асимптотически устойчиво, а периодическое решение, близкое к х = -1 (для него А = — 1 ± л/3), — неустойчиво. Метод отыскания периодических решений при резонансе, то есть когда условие (19) не выполнено, изложен в [13), гл. 2, §8, пункты 2 и 3; примеры там же; в [2], гл. 5, §3, п. 2 и в [33], гл. 2, §6, 7. Об отыскании периодических решений автономной системы х’ = Ах -f pf(x,p) в случае, когда при р = 0 периодическое решение известно, см. [13], гл.2, §8, пункт 4; [2], гл.5, §3, п. 3 и [33], гл.2, §11-13.

Метод малого параметра применялся к широкому кругу задач, в частности, в [33], главы 4-8. Методы последовательных приближений для уравнений с малым параметром разработаны в [24]. Существенно отличным от предыдущих является случай, когда малый параметр является множителем при производной, например, fix = /(*, у), у =д(х, у). Здесь нет непрерывной зависимости от /1 при р 0, и решения имеют другие свойства, см., например, [13], гл.4, §6 и [15], гл.10, §3,4. Известно много работ, в которых подробно исследуются такие случаи.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Нахождение периодических решений дифференциальных уравнений

Пусть дано линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами

где — функция, периодическая с периодом , разлагающаяся в ряд Фурье

Периодическое решение уравнения (47) ищем в виде

Подставляем ряд (49) в уравнение (47) и подбираем его коэффициенты так, чтобы равенство (47) удовлетворялось формально. Приравнивая свободные члены и коэффициенты при и в левых и правых частях полученного равенства, найдем

Первое из равенств (50) дает необходимое условие существования решения вида (49): если , то необходимо, чтобы . Подставляя (50) в (49), получаем

Когда и , где , периодическое решение будет существовать только при условии

Коэффициенты и при расходятся по формулам (50), а коэффициенты и остаются произвольными, так как выражение является общим решением соответствующего однородного уравнения.

В случае невыполнения условий (52) уравнение (47) периодических решений не имеет (возникает резонанс). При и коэффициент остается неопределенным и уравнение (47) имеет бесконечное множество периодических решений, отличающихся друг от друга постоянным слагаемым.

Если правая часть уравнения (47) имеет период , то надо разлагать по периоду и искать решение уравнения (47) в виде

Формулы (50) при этом соответственно изменятся.

Пример 8. Найти периодические решения уравнения .

Решение. Имеем . Функция не содержит резонирующего члена , значит, уравнение имеет периодические решения, притом бесконечное множество. По формулам (50) находим коэффициенты

Все периодические решения даются формулой

где и — произвольные постоянные.

Пример 9. Найти периодические решения уравнения .

Решение. В данном случае . Проверим выполнимость условий (52). Имеем

Условия (6) существования периодического решения не выполняются. Следовательно, данное уравнение периодических решений не имеет. В самом деле, общее решение уравнения есть

которое, очевидно, не является периодическим из-за наличия слагаемого .

Пример 10. Найти периодическое решение уравнения .

Решение. Функция — периодическая с периодом . Разлагаем ее в ряд Фурье в интервале :

Решение данного уравнения ищем в виде

Формулы (50) дают

Следовательно, уравнение имеет периодическое решение вида

ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Иванов Г.Г., Алфёров Г.В., Королёв В.С., Селицкая Е.А.

Сформулированы и доказаны теоремы об оценке числа периодических решений дифференциальных уравнений первого порядка.

Похожие темы научных работ по математике , автор научной работы — Иванов Г.Г., Алфёров Г.В., Королёв В.С., Селицкая Е.А.

PERIODIC SOLUTIONS OF DIFFERENTIAL EQUATIONS

In the paper, the authors formulate and prove theorems on the estimation for the number of periodic solutions of first-order differential equations.

Текст научной работы на тему «ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ»

ВЕСТНИК ПЕРМСКОГО УНИВЕРСИТЕТА

2019 Математика. Механика. Информатика Вып. 3(46)

Периодические решения дифференциальных уравнений

Г. Г. Иванов, Г. В. Алфёров, В. С. Королёв, Е. А. Селицкая

Санкт-Петербургский государственный университет

Россия, 198504, Санкт-Петербург, Петергоф, Университетский проспект, 35 g.alferov@spbu.ru; +7-911-246-57-87

Сформулированы и доказаны теоремы об оценке числа периодических решений дифференциальных уравнений первого порядка.

Ключевые слова: производное число; периодические решения, почти периодические решения; негладкий анализ, производные Дини-Гёльдера.

В работе развивается основанный на идеях функционального анализа метод исследования периодических решений обыкновенных дифференциальных уравнений первого порядка. Изучению периодических решений посвящено большое количество работ. Основы теории периодических решений дифференциальных уравнений разрабатывали Анри Пуанкаре для задачи трех тел [1] и А.М. Ляпунов для задачи о движении любой механической системы [2]. Периодические решения играют существенную роль в качественной теории дифференциальных уравнений и в прикладных задачах [3]. Необходимость анализа периодических решений дифференциальных уравнений возникает в классической и небесной механике 7, космической робототехнике 17, а также при моделировании экономических процессов 31. Однако общего подхода изучения периодических решений дифференциальных уравнений не существует. Имеется несколько методов и способов для решения данной задачи. Так,

© Иванов Г.Г., Алфёров Г.В., Королёв В.С., Селицкая Е.А., 2019

Работа выполнена при финансовой поддержке РФФИ, проект № 18-08-00419.

основным методом доказательства существования периодических решений дифференциальных уравнений являются: метод точечных отображений Пуанкаре-Андронова, метод направляющих функций, вариационные методы, топологический метод, усреднение Крылова-Боголюбова и т.д. Отметим, что перечисленные методы достаточно сложно применять на практике.

В данной работе, опираясь на результаты работ 20 и используя аппарат производных чисел [22], решается задача оценки числа периодических решений дифференциальных уравнений первого порядка.

1. Верхняя оценка числа периодических решений

Пусть правая часть уравнения

есть непрерывная по совокупности аргументов и с -периодическая по г функция.

Теорема 1. Если правая часть уравнения (1) при каждом фиксированном г есть возрастающая по х функция, причем существует момент г * е [0, с] такой, что / (г *, х) строго возрастает, то уравнение (1) может иметь не более одного периодического решения.

Доказательство. Предположим, что вопреки утверждению теоремы, уравнение (1) имеет два периодических решения х (?) и х2 (?) . Покажем, что эти решения не имеют общих точек.

Поскольку х (?) Ф х (?), то существует точка ?0 такая, что х (?о) ^ X (?0) . Не нарушая общности, можно считать, что ?0 = 0

и х (0) 0, что X (Т) = х (Т) . Обозначим через ? точную нижнюю границу множества

0>. В силу непрерывности функций х (?) и х (?) и условия (2) заключаем, что ? > 0 .

Из неравенства (2) и выбора точки ? следует, что при ? е [0, ?] х (?) — х2 (?). По условию теоремы функция / (?, х) возрастает по х при каждом фиксированном ? , и, следовательно, для ? е [0, ? ] будет иметь место неравенство

но тогда, учитывая (2), получим

V? ‘ ) 0 решения х и х не пересекаются. Отсутствие у этих решений общих точек при ? 0.

Более того, поскольку /(?,х) непрерывна и /(?*, х) строго возрастает по х, то в некоторой окрестности точки ?* е [0, с] будет иметь место строгое неравенство / (?, х (?)) 0.

Учитывая последнее неравенство, приходим к следующей противоречивой цепочке соотношений:

0 = [ х2 (с) — х2 (0)] — [ х (с) — х (0)] =

Полученное противоречие и опровергает предположение о том, что в условиях теоремы уравнение (1) может иметь два различных с -периодических решения.

Теорема 2. Если правая часть уравнения (1) при каждом фиксированном ? есть выпуклая функция, причем для некоторого ?* е[0, с] /(?*, х) строго выпуклая по х, то уравнение (1) может иметь не более двух различных с -периодических решений.

Доказательство. Прежде всего покажем, что в условиях теоремы уравнение (1) обладает свойством существования и единственности решения, для чего установим, что если / выпукла и непрерывна, то она является Липшицевой.

Действительно, пусть (?0, х0) — произвольная точка плоскости, а Т и 8 -некоторые положительные числа. Покажем, что для области

Б = <(?, х):? е [?0 — т, ?0 + т], х е [х0 — 8, х0 + 8]>существует такое Ь, что для любых х , х е [х0 — 8, х0 +8] и сразу для всех ? е [?0 — т, ?0 + т] будет

| /(?, х») — /(?, х’)| х0 + 3. Тогда для всех у е (х0 +3, т], учитывая тот факт, что при любом фиксированном г функция

I (г, у) — I (г, хо +3)

возрастает по у, будем

I(г, у) — I(г, хо +3) К и произвольных х , х е [х0 —3, х0 + 3] будет

Кг, х’) — I(г, х’ ) Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

В силу (4) очевидно, что при всех г а(г) е (о,1) .

Подставляя в правую часть (5) представление (6), получим

I (г, уз) — I (г, у 2) I (г, у 2) — I (г, у г) _

а)Уз) _ а(Уз — Уг) / (? ,ау1 + (1 -а)уз) — / (?, ух)_

(1 -а)(Уз — Ух) _ а/(?,У) + (1 -а)/(?,Уз)-/(?,«У + (1 -а)Уз) «(1 -а)(Уз — У1)

Функция g(?) непрерывна, так как непрерывны функции / и а и из неравенства (4) и определения а следует, что существует такое число ¡5 >0, что при всех ? будет

а(?)(1 -а(?))(Уз(?) -у,(?)) >5. Более того, учитывая выпуклость функции / , т.е. что при всех ?

а/(?, У1) + (1 — а)/(?, Уз) > /(?, аух + (1 — а)Уз),

заключаем, что при всех ?

Но при ? = ?* е [0, с] по условию теоремы /(?*, х) строго выпукла, из чего

следует, что как в самой точке ? * , так и в некоторой ее окрестности, в силу непрерывности, будет выполняться строгое неравенство g(?) > 0.

Таким образом, окончательно функция g непрерывна, неотрицательна и существует промежуток, на котором она принимает только положительные значения.

Принимая во внимание эти соображения, проинтегрируем тождество (5) в пределах от 0 до с . Поскольку функции у, У и У с-периодические, то получим

0 0. Таким образом, функция гу(х) задана корректно.

Если дополнительно известно, что у/(х) строго выпукла, то теорему очень просто доказать.

Действительно, пусть уравнение (1) имеет четыре с -периодических решения ф(?, х), начинающиеся в точках хг, 1 = 1,2,3,4 . Пусть, для определенности, х1 ],хе[хх,х4]> функция ф(г, х) ограничена, так как в силу существования и единственности решений уравнения (1) она возрастает по х , и, следовательно, ф(г, х1) 0. Покажем, что

Действительно, учитывая, что функция (I ) + (г, ф(г, х)) возрастает по х, а ф (г, х) > 0, и используя уравнение в вариациях, получим:

Л+ [у + ](х) = ]т—([ (I ) + (гф(г, х

+ К))ф (г, х + К) — (I )’+ (г,ф(г, х))ф(г, х) —г)

= ш — I ф (г, х + Нп)[(/ ) + (г, ф(г, х + Нп))

Отыскание периодических решений одного класса неавтономных систем дифференциальных уравнений

В прикладной математике иногда возникает задача построения периодических решений нормальной системы обыкновенных дифференциальных уравнений вида

где функция 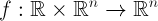представляет собой сумму

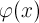
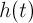
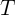
многомерного многочлена и тригонометрического полинома , являющегося -периодической векторной функцией.

Многие из теорем существования периодических решений системы (1) используют тот фундаментальный факт, что такие решения полностью определяются неподвижными точками оператора сдвига по траекториям системы. Однако использование данных теорем для непосредственного нахождения нужного периодического решения, скорее всего, не представляется возможным.

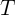
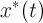
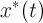
Пусть известно, что система (1) имеет единственное -периодическое решение . Примерами систем, имеющих единственное периодическое решение, являются системы с конвергенцией (Плисс В.А. Нелокальные проблемы теории колебаний. — М., Л.: Наука, 1964). Рассмотрим один класс таких систем, для которого можно построить приближения к решению .

Пусть 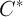— вектор, что

Здесь для простоты рассуждений мы полагаем, что начальный момент времени равен нулю. Тогда, если удастся определить вектор 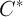, то мы сумеем построить искомое периодическое решение.

Введем условия, накладываемые на функцию :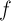

1. Пусть — замкнутый шар радиуса r, содержащий значения решения , — замкнутый шар радиуса R, причем , и существует такое положительное число , что для любых имеет место неравенство

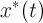
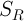
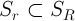
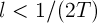
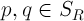
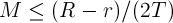
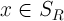
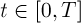
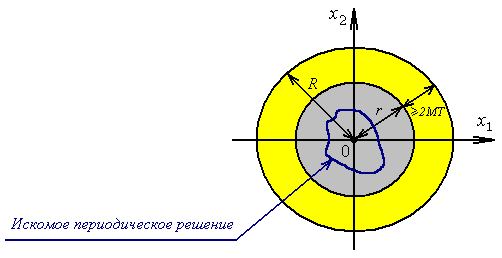
2. Существует такое положительное число , что для всех и любых выполняется неравенство

На рис. 1 приведена графическая иллюстрация этих условий для системы (1) второго порядка.

Рис. 1. Иллюстрация условий 1-2 для системы второго порядка.

В моей работе показано, что в этом случае последовательные приближения

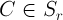
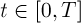
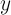
для любого вектора сходятся равномерно для всех к некоторой функции . Причем, если выбрать , то окажется, что

Исходя из формулы (2), каждая итерация вычисляется в символьной форме. При этом после преобразований тригонометрических функций под интегралом всегда можно получить тригонометрический полином с нулевым средним интегральным значением. Аналитическая форма представления приближения к периодическому решению удобна тем, что дает возможность провести анализ гармоник, составляющих это приближение. После вычисления очередной итерации строится функция

минимум которой и даст приближение к вектору .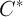

В качестве примера была рассмотрена нелинейная система второго порядка с конвергенцией вида (1) (в работе указаны значения радиусов шаров), где

. Обнаружено, что на первой и второй итерациях значения найденных приближений к вектору одинаковы, и

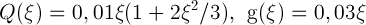
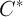
Проверено, что траектория исследуемой системы второго порядка, соответствующая найденной начальной точке, возвращается в ее окрестность через период (рис. 2).

Рис. 2. Дуга траектории, соответствующей найденному вектору .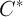

По данной теме можно посмотреть мой доклад на математической конференции (прошу прощения за качество видео — снимали на телефон).

Функция

называется периодическим решением,
если для всех t
и некоторого периода

выполняется равенство

(2.22)

Периодическое
решение представляется рядом Фурье,
содержащим некоторую составляющую с
циклической частотой

и гармоники, расположенные равномерно
(эквидистантно) с частотами

,
где k
= 2,3,… При этом ненулевую амплитуду могут
иметь не все указанные спектральные
составляющие.

В
произвольной неавтономной ДС обычно
значение

кратно периоду Т внешнего возмущающего
воздействия с коэффициентом кратности
k
= 1,2,… Если

, такое решение называется субгармоническим
k
– го порядка. Изолированное периодическое
решение

для автономной ДС называется предельным
циклом. Предельный цикл представляет
собой самоподдерживающееся колебание
и не может возникать в линейных ЭЭС.

К
лассический
пример предельного цикла обнаруживается
при исследовании решений уравнения Ван
дер Поля

(2.23)

Существование
предельного цикла Ван дер Поля можно
объяснить, если представить систему
дифференциальных уравнений (2.23) в виде
скалярного дифференциального уравнения

(2.24)

Демпфирующий
член этого уравнения содержит коэффициент

,
который имеет отрицательное значение
при

,
что означает получение решения с
нарастающей амплитудой, и положительное
значение при

,
что соответствует решению с убывающей
амплитудой. Поскольку траектории,
исходящие из области вблизи начала
координат, «расширяются», траектории,
исходящие из внешних областей, «сжимаются»,
а единственное положение равновесия
располагается в нуле, должен существовать
предельный цикл, охватывающий начало
координат. В противном случае траектории
должны были бы пересекаться, так как
они располагаются на одной и той же
плоскости.

Предельное
множество, соответствующее предельному
циклу, представляет собой замкнутую
кривую, описываемую решением

за один период.

Как
известно, периодическому решению системы
дифференциальных уравнений соответствует
некоторая неподвижная точка отображения
Пуанкаре R.
Определения отображения Пуанкаре
различаются для автономных и неавтономных
ДС. Для неавтономных ДС отображение R
определяется равенством

.

Отображение
R
можно рассматривать с двух позиций:

а)
R(x)
указывает, где под действием векторного
потока окажется точка х
по истечении Т секунд;

б)
орбита

представляет собой выборку одной
траектории каждые T
секунд.

Это означает, что

.
(2.25)

Выполнение
таких операций аналогично действию
стробоскопа, вспыхивающего с периодом
Т.

Для
автономных ДС отображение Пуанкаре R
определяется только в некоторой
окрестности точки предельного цикла
Г, при этом не гарантируется изменение
положения точки х.

По
аналогии с положением равновесия
устойчивость неподвижной точки х*
отображения R
можно определить, если произвести
линеаризацию отображения R
в этой точке. Локальное поведение
отображения R
вблизи точки х*
описывается линейной системой уравнений
с дискретным временем вида

.
(2.26)

Орбита
отображения R
для начального условия

в линейном приближении определяется
уравнением

,
(2.27)

где

,

– собственные значения и собственные
векторы матрицы R(x*);

– скалярные константы, определяемые
начальным условием; P=n
для неавтономных и P=n
– 1 для автономных систем дифференциальных
уравнений.

Собственные
значения

представляют собой характеристические
множители для рассматриваемой неподвижной
точки; определяют степень сжатия (при

)
и растяжения (при

)
соответствующей траектории вблизи
точки х*
в направлении, определяемом вектором

для
одной итерации отображения R.

Такие
характеристические множители определяют
устойчивость периодического решения.
Периодическое решение является
асимптотически устойчивым, если все
собственные значения

располагаются строго внутри единичной
окружности. Периодическое решение
является вполне неустойчивым, если
неравенство

выполняется для всех

;
периодическое решение просто неустойчиво,
если одни значения

располагаются внутри единичной
окружности, другие вне ее. По аналогии
с положением равновесия гиперболическими
называются периодические решения,
которые не имеют характеристических
множителей на единичной окружности.
Гиперболические периодические решения
являются структурно устойчивыми. В тех
случаях, когда хотя бы один характеристический
множитель располагается на единичной
окружности, устойчивость соответствующего
ему периодического решения не может
быть определена с использованием
характеристических множителей без
привлечения других средств.

Характеристические
множители в случае неавтономных ДС
определяются через матрицу R(x*),
которая представляет собой якобиан n
– вектора

по n
– мерному вектору

,
вычисляемой в точке

,
т.е. матрица R(x*)
представляет собой переходную матрицу
состояний системы дифференциальных
уравнений

.
(2.28)

Таким
образом, матрица – функция

определяет
эволюцию малых возмущений во времени.
В тех случаях, когда время t
фиксировано, а вектор

достаточно мал по модулю, в линейном
приближении можно записать

.
(2.29)

Такая
интерпретация имеет смысл, поскольку
функция F
была определена как производная (якобиан)
от функции

по начальному значению.

Характеристические
множители в случае автономных ДС
определяются с помощью уравнения в
вариациях

,
(2.30)

а
решением этого уравнения является
матрица

.
Собственные значения матрицы

совпадают с (n–1)
характеристическими множителями, а еще
одно собственное значение всегда равно
единице.

Итак,
можно отметить, что характеристические
множители отражают степень сжатия или
растяжения траектории за один период
в области, располагаемой вблизи
какого-либо периодического решения.
При этом n
характеристических множителей
периодического решения неавтономной
ДС представляют собой собственные
значения матрицы

.
В случае автономной ДС собственные
значения матрицы

представляют собой характеристические
множители предельного цикла.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Нахождение периодических решений дифференциальных уравнений

Пусть дано линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами

где — функция, периодическая с периодом , разлагающаяся в ряд Фурье

Периодическое решение уравнения (47) ищем в виде

Подставляем ряд (49) в уравнение (47) и подбираем его коэффициенты так, чтобы равенство (47) удовлетворялось формально. Приравнивая свободные члены и коэффициенты при и в левых и правых частях полученного равенства, найдем

Первое из равенств (50) дает необходимое условие существования решения вида (49): если , то необходимо, чтобы . Подставляя (50) в (49), получаем

Когда и , где , периодическое решение будет существовать только при условии

Коэффициенты и при расходятся по формулам (50), а коэффициенты и остаются произвольными, так как выражение является общим решением соответствующего однородного уравнения.

В случае невыполнения условий (52) уравнение (47) периодических решений не имеет (возникает резонанс). При и коэффициент остается неопределенным и уравнение (47) имеет бесконечное множество периодических решений, отличающихся друг от друга постоянным слагаемым.

Если правая часть уравнения (47) имеет период , то надо разлагать по периоду и искать решение уравнения (47) в виде

Формулы (50) при этом соответственно изменятся.

Пример 8. Найти периодические решения уравнения .

Решение. Имеем . Функция не содержит резонирующего члена , значит, уравнение имеет периодические решения, притом бесконечное множество. По формулам (50) находим коэффициенты

Все периодические решения даются формулой

где и — произвольные постоянные.

Пример 9. Найти периодические решения уравнения .

Решение. В данном случае . Проверим выполнимость условий (52). Имеем

Условия (6) существования периодического решения не выполняются. Следовательно, данное уравнение периодических решений не имеет. В самом деле, общее решение уравнения есть

которое, очевидно, не является периодическим из-за наличия слагаемого .

Пример 10. Найти периодическое решение уравнения .

Решение. Функция — периодическая с периодом . Разлагаем ее в ряд Фурье в интервале :

Решение данного уравнения ищем в виде

Формулы (50) дают

Следовательно, уравнение имеет периодическое решение вида

РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Простейшими тригонометрическими уравнениями называют уравнения

Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.

19.1. Уравнение cos x = a

Объяснение и обоснование

1. Корни уравненияcosx=a.

При |a| > 1 уравнение не имеет корней, поскольку |cos x| ≤ 1 для любого x (прямая y = a на рисунке из пункта 1 таблицы 1 при a > 1 или при a 1 уравнение не имеет корней, поскольку |sin x| ≤ 1 для любого x (прямая y = a на рисунке 1 при a > 1 или при a n arcsin a + 2πn, n ∈ Z (3)

2.Частые случаи решения уравнения sin x = a.

Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).

Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда

Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,

Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,

Примеры решения задач

Замечание. Ответ к задаче 1 часто записывают в виде:

19.3. Уравнения tg x = a и ctg x = a

Объяснение и обоснование

1.Корни уравнений tg x = a и ctg x = a

Рассмотрим уравнение tg x = a. На промежутке функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x₁ = arctg a и для этого корня tg x = a.

Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:

При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).

Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x₁=arсctg a.

Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:

таким образом, уравнение ctg x = 0 имеет корни

Примеры решения задач

Вопросы для контроля

1. Какие уравнения называют простейшими тригонометрическими?
2. Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
3. Выведите формулы решения простейших тригонометрических уравнений.
4. Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.

Упражнения

Решите уравнение (1-11)

Найдите корни уравнения на заданном промежутке (12-13)

Алгебра

План урока:

Простейшие показательные уравнения а х = b

Его называют показательным уравнением, ведь переменная находится в показателе степени. Для его решения представим правую часть как степень числа 2:

Тогда уравнение будет выглядеть так:

Теперь и справа, и слева стоят степени двойки. Очевидно, что число 3 будет являться его корнем:

Является ли этот корень единственным? Да, в этом можно убедиться, если построить в координатной плоскости одновременно графики у = 2 х и у = 8. Второй график представляет собой горизонтальную линию.

Пересекаются эти графики только в одной точке, а потому найденное нами решение х = 3 является единственным.

Так как любая показательная функция является монотонной, то есть либо только возрастает (при основании, большем единицы), либо только убывает (при основании, меньшем единицы), то в общем случае ур-ние а х = b может иметь не более одного решения. Это является следствием известного свойства монотонных функций – горизонтальная линия пересекает их не более чем в одной точке.

Сразу отметим, что если в ур-нии вида а х = b число b не является положительным, то корней у ур-ния не будет вовсе. Это следует из того факта, что область значений показательной функции – промежуток (0; + ∞), ведь при возведении в степень любого положительного числа результат всё равно остается положительным. Можно проиллюстрировать это и графически:

Решая простейшее показательное уравнение

мы специально представляли правую часть как степень двойки:

После этого мы делали вывод, что если в обеих частях ур-ния стоят степени с равными основаниями (2 = 2), то у них должны быть равны и показатели. Это утверждение верно и в более общем случае. Если есть ур-ние вида

то его единственным решением является х = с.

Задание. Найдите решение показательного уравнения

Решение. У обоих частей равны основания, значит, равны и показатели:

Задание. Найдите корень уравнения

Решение. Заметим, что число 625 = 5 4 . Тогда ур-ние можно представить так:

Отсюда получаем, что х = 4.

Видно, что основной метод решения показательных уравнений основан на его преобразовании, при котором и в правой, и в левой части стоят степени с совпадающими основаниями.

Задание. При каком х справедливо равенство

Решение. Преобразуем число справа:

Теперь ур-ние можно решить:

Задание. Решите ур-ние

Решение. Любое число при возведении в нулевую степень дает единицу, а потому можно записать, что 1 = 127 0 . Заменим с учетом этого правую часть равенства:

Уравнения вида а f( x) = a g ( x)

Рассмотрим чуть более сложное показательное ур-ние

Для его решения заменим показатели степеней другими величинами:

Теперь наше ур-ние принимает вид

Такие ур-ния мы решать умеем. Надо лишь приравнять показатели степеней:

При решении подобных ур-ний введение новых переменных опускают. Можно сразу приравнять показатели степеней, если равны их основания:

В общем случае использованное правило можно сформулировать так:

Задание. Найдите корень ур-ния

Решение. Представим правую часть как степень двойки:

Тогда ур-ние примет вид

Теперь мы имеем право приравнять показатели:

Задание. Укажите значение х, для которого выполняется условие

Решение. Здесь удобнее преобразовать не правую, а левую часть. Заметим, что

С учетом этого можно записать

Основания у выражений слева и справа совпадают, а потому можно приравнять показатели:

Задание. Укажите корень показательного уравнения

Решение. Для перехода к одному основанию представим число 64 как квадрат восьми:

Тогда ур-ние примет вид:

Задание. Найдите корень ур-ния

Решение. Здесь ситуация чуть более сложная, ведь число 2 невозможно представить как степень пятерки, а пятерки не получится выразить как степень двойки. Однако у обеих степеней в ур-нии совпадают показатели. Напомним, что справедливы следующие правила работы со степенями:

С учетом этого поделим обе части ур-ния на выражения 5 3+х :

Задание. При каких х справедлива запись

Можно сделать преобразования, после которых в ур-нии останется только показательная функция 5 х . Для этого произведем следующие замены:

Перепишем исходное ур-ние с учетом этих замен:

Теперь множитель 5 х можно вынести за скобки:

Рассмотрим чуть более сложное ур-ние, которое может встретиться на ЕГЭ в задании повышенной сложности №13.

Задание. Найдите решение уравнения

Решение. Преобразуем левое слагаемое:

Перепишем начальное ур-ние, используя это преобразование

Теперь мы можем спокойно вынести множитель за скобки:

Получили одинаковые основания слева и справа. Значит, можно приравнять и показатели:

Это квадратное уравнение, решение которого не должно вызывать у десятиклассника проблем:

Задачи, сводящиеся к показательным уравнениям

Рассмотрим одну прикладную задачу, встречающуюся в ЕГЭ по математике.

Задание. Из-за радиоактивного распада масса слитка из изотопа уменьшается, причем изменение его массы описывается зависимостью m(t) = m₀ • 2 – t/ T , где m₀ – исходная масса слитка, Т – период полураспада, t – время. В начальный момент времени изотоп, чей период полураспада составляет 10 минут, весит 40 миллиграмм. Сколько времени нужно подождать, чтобы масса слитка уменьшилась до 5 миллиграмм.

Решение. Подставим в заданную формулу значения из условия:

m₀ = 40 миллиграмм;

m(t) = 5 миллиграмм.

В результате мы получим ур-ние

из которого надо найти значение t. Поделим обе части на 40:

Далее решим чуть более сложную задачу, в которой фигурирует сразу 2 радиоактивных вещества.

Задание. На особо точных рычажных весах в лаборатории лежат два слитка из радиоактивных элементов. Первый из них весит в начале эксперимента 80 миллиграмм и имеет период полураспада, равный 10 минутам. Второй слиток весит 40 миллиграмм, и его период полураспада составляет 15 минут. Изначально весы наклонены в сторону более тяжелого слитка. Через сколько минут после начала эксперимента весы выровняются? Масса слитков меняется по закону m(t) = m₀ • 2 – t/ T , где m₀ и Т – это начальная масса слитка и период его полураспада соответственно.

Решение. Весы выровняются тогда, когда массы слитков будут равны. Если подставить в данную в задаче формулу условия, то получится, что масса первого слитка меняется по закону

а масса второго слитка описывается зависимостью

Приравняем обе формулы, чтобы найти момент времени, когда массы слитков совпадут (m₁ = m₂):

Делим обе части на 40:

Основания равны, а потому приравниваем показатели:

Уравнения с заменой переменных

В ряде случаев для решения показательного уравнения следует ввести новую переменную. В учебных заданиях такая замена чаще всего (но не всегда) приводит к квадратному ур-нию.

Задание. Решите уравнение методом замены переменной

Заметим, что в уравнении стоят степени тройки и девятки, но 3 2 = 9. Тогда введем новую переменную t = 3 x . Если возвести ее в квадрат, то получим, что

C учетом этого изначальное ур-ние можно переписать:

Получили обычное квадратное ур-ние. Решим его:

Мы нашли два значения t. Далее необходимо вернуться к прежней переменной, то есть к х:

Первое ур-ние не имеет решений, ведь показательная функция может принимать лишь положительные значения. Поэтому остается рассмотреть только второе ур-ние:

Задание. Найдите корни ур-ния

Решение. Здесь в одном ур-нии стоит сразу три показательных функции. Попытаемся упростить ситуацию и избавиться от одной из них. Для этого поделим ур-ние на выражение 4 4х+1 :

Так как 1 4х+1 = 1, мы можем записать:

Обратим внимание, что делить ур-ние на выражение с переменной можно лишь в том случае, если мы уверены, что оно не обращается в ноль ни при каких значениях х. В данном случае мы действительно можем быть в этом уверены, ведь величина 4 4х+1 строго положительна при любом х.

Вернемся к ур-нию. В нем стоят величины (9/4) 4х+1 и (3/2) 4х+1 . У них одинаковые показатели, но разные степени. Однако можно заметить, что

9/4 = (3/2) 2 , поэтому и (9/4) 4х+1 = ((3/2) 4х+1 ) 2 . Это значит, что перед нами уравнение с заменой переменных.

Произведем замену t = (3/2) 4х+1 , тогда (9/4) 4х+1 = ((3/2) 4х+1 ) 2 = t 2 . Далее перепишем ур-ние с новой переменной t:

Снова получили квадратное ур-ние.

Возвращаемся к переменной х:

И снова первое ур-ние не имеет корней, так как при возведении положительного числа в степень не может получится отрицательное число. Остается решить второе ур-ние:

Графическое решение показательных уравнений

Не всякое показательное уравнение легко или вообще возможно решить аналитическим способом. В таких случаях выручает графическое решение уравнений.

Задание. Найдите графическим способом значение х, для которого справедливо равенство

Решение. Построим в одной системе координат графики у = 3 х и у = 4 – х:

Видно, что графики пересекаются в одной точке с примерными координатами (1; 3). Так как графический метод не вполне точный, следует подставить х = 1 в ур-ние и убедиться, что это действительно корень ур-ния:

Получили верное равенство, значит, х = 1 – это действительно корень ур-ния.

Задание. Решите графически ур-ние

Решение. Перенесем вправо все слагаемые, кроме 2 х :

Слева стоит показательная функция, а справа – квадратичная. Построим их графики и найдем точки пересечения:

Видно, что у графиков есть две общие точки – это (0;1) и (1; 2). На всякий случай проверим себя, подставив х = 0 и х = 1 в исходное ур-ние:

Ноль подходит. Проверяем единицу:

И единица тоже подошла. В итоге имеем два корня, 0 и 1.

Показательные неравенства

Рассмотрим координатную плоскость, в которой построен график некоторой показательной ф-ции у = а х , причем а > 0. Пусть на оси Ох отложены значения s и t, и t t и a s на оси Оу. Так как

является возрастающей функцией, то и величина a t окажется меньше, чем a s . Другими словами, точка a t на оси Оу будет лежать ниже точки а s (это наглядно видно на рисунке). Получается, что из условия t t s . Это значит, что эти два нер-ва являются равносильными.

С помощью этого правила можно решать некоторые простейшие показательные неравенства. Например, пусть дано нер-во

Представим восьмерку как степень двойки:

По только что сформулированному правилу можно заменить это нер-во на другое, которое ему равносильно:

Решением же этого линейного неравенства является промежуток (– ∞; 3).

Однако сформулированное нами правило работает тогда, когда основание показательной ф-ции больше единицы. А что же делать в том случае, если оно меньше единицы? Построим график такой ф-ции и снова отложим на оси Ох точки t и s, причем снова t будет меньше s, то есть эта точка будет лежать левее.

Так как показательная ф-ция у = а х при основании, меньшем единицы, является убывающей, то окажется, что на оси Оу точка a s лежит ниже, чем a t . То есть из условия t t > a s . Получается, что эти нер-ва равносильны.

Например, пусть надо решить показательное неравенство

Выразим число слева как степень 0,5:

Тогда нер-во примет вид

По рассмотренному нами правилу его можно заменить на равносильное нер-во

В более привычном виде, когда выражение с переменной стоит слева, нер-во будет выглядеть так:

а его решением будет промежуток (3; + ∞).

В общем случае мы видим, что если в показательном нер-ве вида

основание a больше единицы, то его можно заменить равносильным нер-вом

Грубо говоря, мы просто убираем основание степеней, а знак нер-ва остается неизменным. Если же основание а меньше единицы, то знак неравенства необходимо поменять на противоположный:

Это правило остается верным и в том случае, когда вместо чисел или переменных t и s используются произвольные функции f(x) и g(x). Сформулируем это правило:

Таким образом, для решения показательных неравенств их следует преобразовать к тому виду, при котором и справа, и слева стоят показательные ф-ции с одинаковыми показателями, после чего этот показатель можно просто отбросить. Однако надо помнить, что при таком отбрасывании знак нер-ва изменится на противоположный, если показатель меньше единицы.

Задание. Решите простейшее неравенство

Представим число 64 как степень двойки:

теперь и справа, и слева число 2 стоит в основании. Значит, его можно отбросить, причем знак нер-ва останется неизменным (ведь 2 > 1):

Задание. Найдите промежуток, на котором выполняется нер-во

Решение. Так как основание степеней, то есть число 0,345, меньше единицы, то при его «отбрасывании» знак нер-ва должен измениться на противоположный:

Это самое обычное квадратное неравенство. Для его решения нужно найти нули квадратичной функции, стоящей слева, после чего отметить их на числовой прямой и определить промежутки, на которых ф-ция будет положительна.

Нашли нули ф-ции. Далее отмечаем их на прямой, схематично показываем параболу и расставляем знаки промежутков:

Естественно, что в более сложных случаях могут использоваться всё те же методы решения нер-ва, которые применяются и в показательных ур-ниях. В частности, иногда приходится вводить новую переменную.

Задание. Найдите решение нер-ва

Решение. Для начала представим число 3 х+1 как произведение:

Теперь перепишем с учетом этого исходное нер-во:

Получили дробь, в которой есть одна показательная ф-ция 3 х . Заменим её новой переменной t = 3 x :

Это дробно-рациональное неравенство, которое можно заменить равносильным ему целым нер-вом:

которое, в свою очередь, решается методом интервалов. Для этого найдем нули выражения, стоящего слева

Отмечаем найденные нули на прямой и расставляем знаки:

Итак, мы видим, что переменная t должна принадлежать промежутку (1/3; 9), то есть

Теперь произведем обратную замену t = 3 x :

Так как основание 3 больше единицы, просто откидываем его:

Итак, мы узнали о показательных уравнениях и неравенствах и способах их решения. В большинстве случаев необходимо представить обе части равенства или неравенства в виде показательных степеней с одинаковыми основаниями. Данное действие иногда называют методом уравнивания показателей. Также в отдельных случаях может помочь графический способ решения ур-ний и замена переменной.