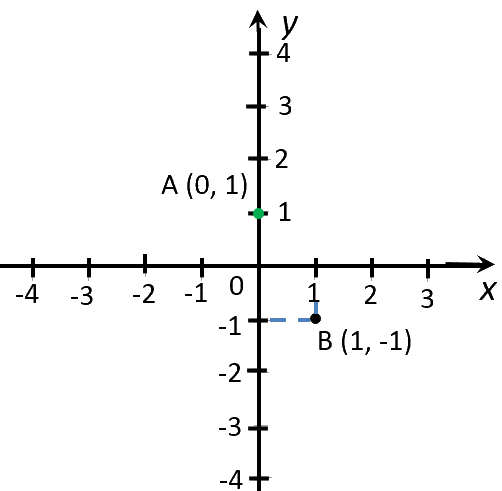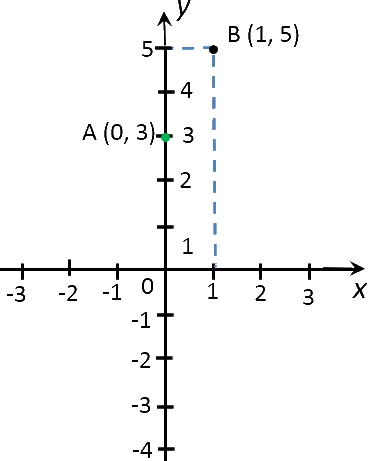Как найти перпендикуляр графика

Взаимосвязь между двумя линиями, пересекающимися под прямым углом (90 градусов) Отрезок AB перпендикулярен сегменту CD, поскольку два угла, которые он создает (обозначены оранжевым и синим), составляют каждый по 90 градусов. Отрезок AB можно назвать перпендикуляром от A к отрезку CD, используя слово «перпендикуляр» как существительное. Точка B называется основанием перпендикуляра от A до сегмента CD или просто основанием A на CD.

В элементарной геометрии свойство быть перпендикуляром (перпендикулярность ) — это отношение между двумя линиями , которые встречаются под прямым углом (90 градусов ). Свойство распространяется на другие связанные геометрические объекты.

Линия считается перпендикулярной другой линии, если две прямые пересекаются под прямым углом. Явно первая линия перпендикулярна второй линии, если (1) две линии встречаются; и (2) в точке пересечения прямой угол на одной стороне первой линии разрезается второй линией на два конгруэнтных угла. Можно показать, что перпендикулярность является симметричной, то есть если первая линия перпендикулярна второй линии, то вторая линия также перпендикулярна первой. По этой причине мы можем говорить о двух линиях как о перпендикулярных (друг другу) без указания порядка.

Перпендикулярность легко распространяется на сегменты и лучи. Например, отрезок линии AB ¯ { displaystyle { overline {AB}}}перпендикулярен отрезку линии CD ¯ { displaystyle { overline {CD}}}если каждая из них вытягивается в обоих направлениях, образуя бесконечную линию, эти две результирующие линии перпендикулярны в указанном выше смысле. В символах A B ¯ ⊥ C D ¯ { displaystyle { overline {AB}} perp { overline {CD}}}означает, что отрезок AB перпендикулярен отрезку линии CD. Информацию о символе перпендикуляра см. В разделе Верхний галс.

Линия считается перпендикулярной плоскости , если она перпендикулярна каждой линии в плоскости, которую она пересекает. Это определение зависит от определения перпендикулярности между линиями.

Две плоскости в пространстве называются перпендикулярными, если двугранный угол, под которым они встречаются, является прямым углом (90 градусов).

Перпендикулярность — это частный пример более общей математической концепции ортогональности ; перпендикулярность — это ортогональность классических геометрических объектов. Таким образом, в высшей математике слово «перпендикуляр» иногда используется для описания гораздо более сложных геометрических условий ортогональности, например, между поверхностью и ее нормалью.

Содержание

• 1 фут перпендикуляра
• 2 Построение перпендикуляра
• 3 Относительно параллельных прямых
• 4 При вычислении расстояний
• 5 График функций
• 6 В кругах и других конусах
  • 6.1 Окружности
  • 6.2 Эллипсы
  • 6.3 Параболы
  • 6.4 Гиперболы
• 7 В многоугольниках
  • 7.1 Треугольники
  • 7.2 Четырехугольники
• 8 Трехмерные линии
• 9 См. Также
• 10 Примечания
• 11 Ссылки
• 12 Внешние ссылки

Фунда перпендикуляра

Слово стопа часто используется в связи с перпендикулярами. Это использование проиллюстрировано на верхней диаграмме выше и в ее заголовке. Схема может быть в любой ориентации. Стопа не обязательно внизу.

Точнее, пусть A будет точкой, а m — прямой. Если B — точка пересечения m и единственной прямой, проходящей через A, которая перпендикулярна m, то B называется основанием этого перпендикуляра, проходящего через A.

Построение перпендикуляра

Построение перпендикуляра (синий) к линии AB через точку P. Построение перпендикуляра к полуоси h из точки P (применимо не только в конечной точке A, M выбирается произвольно), анимация в конце с паузой 10 с

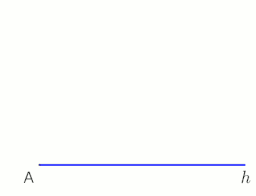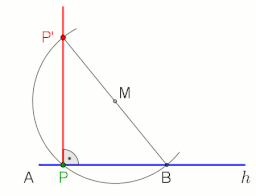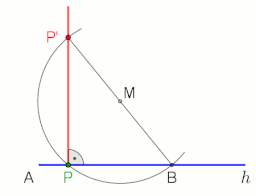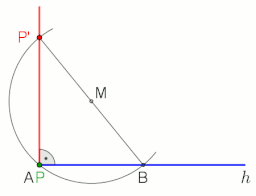
Чтобы провести перпендикуляр к линии AB через точку P с помощью построения циркуля и линейки, действуйте следующим образом (см. Рисунок слева):

• Шаг 1 (красный): постройте круг с центром в точке P для создания точек A ‘и B’ на линии AB, которые находятся на равноудалении от P.
• Шаг 2 (зеленый): построить круги с центром у A ‘и B’ равный радиус. Пусть Q и P — точки пересечения этих двух окружностей.
• Шаг 3 (синий): соедините Q и P, чтобы построить желаемый перпендикуляр PQ.

Чтобы доказать, что PQ перпендикулярен AB, используйте теорему сравнения SSS для ‘и QPB’, чтобы сделать вывод, что углы OPA ‘и OPB’ равны. Затем используйте теорему сравнения SAS для треугольников OPA ‘и OPB’, чтобы сделать вывод, что углы POA и POB равны.

Чтобы провести перпендикуляр к линии g в точке P или через нее, используя теорему Фалеса, см. Анимацию справа.

Теорема Пифагора может быть использована как основа методов построения прямых углов. Например, посчитав звенья, можно сделать три отрезка цепи с длинами в соотношении 3: 4: 5. Их можно выложить в виде треугольника, у которого будет прямой угол напротив его самой длинной стороны. Этот метод полезен для разбивки садов и полей, где размеры велики и не требуется большой точности. Цепи можно использовать повторно, когда это необходимо.

По отношению к параллельным линиям

Знаки стрелок указывают на то, что линии a и b, отрезанные поперечной линией c, параллельны.

Если две прямые (a и б) оба перпендикулярны третьей линии (в), все углы, образованные вдоль третьей линии, являются прямыми углами. Следовательно, в евклидовой геометрии любые две прямые, которые обе перпендикулярны третьей линии, параллельны друг другу из-за постулата параллельности. И наоборот, если одна линия перпендикулярна второй линии, она также перпендикулярна любой линии, параллельной этой второй линии.

На рисунке справа все углы, заштрихованные оранжевым, конгруэнтны друг другу, а все углы, заштрихованные зеленым, конгруэнтны друг другу, поскольку вертикальные углы совпадают и чередующиеся внутренние углы, образованные поперечными параллельными линиями разреза, совпадают. Следовательно, если прямые a и b параллельны, любой из следующих выводов приводит ко всем остальным:

• Один из углов на диаграмме — прямой угол.
• Один из углов, заштрихованных оранжевым. конгруэнтна одному из углов, закрашенных зеленым.
• Линия c перпендикулярна линии a.
• Линия c перпендикулярна линии b.

При вычислении расстояний

Расстояние от точки до линии — это расстояние до ближайшей точки на этой линии. Это точка, в которой отрезок от нее до данной точки перпендикулярен прямой.

Аналогично, расстояние от точки до кривой измеряется отрезком линии, перпендикулярным касательной линии к кривой в ближайшей точке на кривая.

Перпендикулярная регрессия подгоняет линию к точкам данных за счет минимизации суммы квадратов перпендикулярных расстояний от точек данных до линии.

Расстояние от точки до плоскости измеряется как длина от точки вдоль сегмента, перпендикулярного плоскости, то есть перпендикулярно всем линиям в плоскости, которые пройти через ближайшую точку на плоскости к данной точке.

График функций

В двумерной плоскости прямые углы могут быть образованы двумя пересекающимися линиями, если произведение их наклонов равно −1. Таким образом, определяя две линейные функции : y 1 = a 1 x + b 1 и y 2 = a 2 x + b 2, графики функций будут перпендикулярны и образуют четыре прямых угла в местах пересечения линий, если a 1a2= −1. Однако этот метод нельзя использовать, если наклон равен нулю или не определен (линия параллельна оси).

Для другого метода пусть две линейные функции имеют вид: a 1 x + b 1 y + c 1 = 0 и a 2 x + b 2 y + c 2 = 0. Линии будут перпендикулярными тогда и только тогда, когда a 1a2+ b 1b2= 0. Этот метод упрощен из скалярного произведения (или, в более общем смысле, внутреннего произведения ) векторов . В частности, два вектора считаются ортогональными, если их внутренний продукт равен нулю.

В кругах и других кониках

Окружности

Каждый диаметр круга окружности перпендикулярен касательной . к этой окружности в точке, где диаметр пересекает окружность.

Отрезок, проходящий через центр окружности пополам хорду, перпендикулярен хорде.

Если пересечение любых двух перпендикулярных хорд делит одну хорду на длины a и b и делит другую хорду на длины c и d, то a + b + c + d равно квадрату диаметра.

Сумма квадратов длин любых двух перпендикулярных хорд, пересекающихся в данной точке, такая же, как и у любых других двух перпендикулярных хорд, пересекающихся в той же точке, и задается формулой 8r — 4p (где r — длина окружности радиус, а p — расстояние от центральной точки до точки пересечения).

Теорема Фалеса утверждает, что две прямые, проходящие через одну и ту же точку на окружности, но проходящие через противоположные конечные точки диаметра, перпендикулярны. Это эквивалентно тому, что любой диаметр окружности образует прямой угол в любой точке окружности, кроме двух конечных точек диаметра.

Эллипсы

Большая и малая оси эллипса перпендикулярны друг другу и касательным линиям к эллипсу в точках, где оси пересекают эллипс.

Большая ось эллипса перпендикулярна направляющей и каждой прямой кишке.

Параболе

в параболе ось симметрии перпендикулярна прямой кишке, директрисе и касательной в точке, где ось пересекает параболу.

От точки на касательной к вершине параболы другая касательная линия к параболе перпендикулярна прямой, идущей от этой точки через фокус параболы.

ортоптическое свойство параболы заключается в том, что если две касательные к параболе перпендикулярны друг другу, то они пересекаются по направляющей. И наоборот, две касательные, пересекающиеся на директрисе, перпендикулярны. Это означает, что если смотреть из любой точки на своей директрисе, любая парабола имеет прямой угол.

Гиперболы

Поперечная ось гиперболы перпендикулярна сопряженной оси и каждой направляющей.

Произведение перпендикулярных расстояний от точки P на гиперболе или на ее сопряженной гиперболе до асимптот является константой, не зависящей от местоположения P.

A прямоугольная гипербола имеет асимптоты, которые перпендикулярны друг другу. Его эксцентриситет равен 2. { displaystyle { sqrt {2}}.}

В многоугольниках

Треугольники

Катеты прямоугольного треугольника перпендикулярны друг другу.

высоты треугольника перпендикулярны их соответствующим основаниям. серединные перпендикуляры сторон также играют важную роль в геометрии треугольника.

Линия Эйлера равнобедренного треугольника перпендикулярна основанию треугольника.

Теорема о прямой линии Дроза-Фарни касается свойства двух перпендикулярных прямых, пересекающихся в ортоцентре.

треугольника.

Теорема Харкурта касается отношения отрезков прямой через вершина и перпендикулярна любой прямой касательной к треугольнику , вписанной в круг.

Четырехугольники

в квадрате или другом прямоугольнике , все пары смежных сторон перпендикулярны. Правая трапеция — это трапеция , имеющая две пары смежных сторон, перпендикулярных.

Каждая из четырех солодов четырехугольника является перпендикуляром к стороне, проходящей через среднюю точку противоположной стороны.

Ортодиагональный четырехугольник — это четырехугольник, диагонали перпендикулярны. К ним относятся квадрат, ромб и воздушный змей. Согласно теореме Брахмагупты в ортодиагональном четырехугольнике, который также является циклическим, линия, проходящая через середину одной стороны и точку пересечения диагоналей, перпендикулярна противоположной стороне.

Согласно теореме ван Обеля, если квадраты построены снаружи по сторонам четырехугольника, отрезки прямых, соединяющие центры противоположных квадратов, перпендикулярны и равны по длине.

Линии в трех измерениях

До трех линий в трехмерном пространстве могут быть попарно перпендикулярны, например, оси x, y и z трех -мерная декартова система координат.

См. также

Примечания

Ссылки

• Альтшиллер-Корт, Натан (1925), Геометрия колледжа: Введение в Современная геометрия треугольника и круга (2-е изд.), Нью-Йорк: Barnes Noble, LCCN 52-13504
• Кей, Дэвид К. (1969)), College Geometry, Нью-Йорк: Холт, Райнхарт и Уинстон, LCCN 69-12075

Внешние ссылки

Вывод уравнения нормали к графику функции

Евгений Николаевич Беляев

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Замечание 1

Нормаль — это прямая, которая образует с касательной к графику функции угол в $90°$.

Рисунок 1. Нормальный перпендикуляр к графику касательной. Автор24 — интернет-биржа студенческих работ

В связи с тем, что нормаль перпендикулярна к касательной, её угловой коэффициент будет величиной, обратной к угловому коэффициенту касательной:

$k_{норм}=- frac{1}{k_{к}}= -1 frac{1}{f’(x_0)}$.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Пользуясь полученным выводом, запишем уравнение нормали к графику функции:

$y – y_0 = — frac{1}{f’(x_0)} cdot (x – x_0) left(1right) $, здесь $x_0$ и $y_0$ — координаты точки для которой строится искомая линия, при этом производная в этой точке $f’(x_0) ≠ 0$.

Порядок действий при поиске уравнения нормальной прямой если задана координата $x_0$:

1. Вычисляется, чему равен нулевой игрек $y(x_0)$ для функции.
2. Затем нужно определить производную.
3. Нужно высчитать затем, чему равен $f’(x)$ в точке $x_0$, найденное значение — коэффициент касательной.
4. Все найденные значения подставляются в формулу $(1)$.

Напомним также как выглядит само уравнение касательной:

$y – y_0 = f’(x_0) cdot (x – x_0)$.

Пример 1

Найдите уравнение нормали для функции $y=x^2$ в точке $x_0=2$.

Решение:

Производная данной функции составит $y’(x) = 2x$, затем найдём, чему равен наш подопытный кролик-функция в заданной точке $y_0= x^2 = 2^2 = 4$.

Теперь нужно высчитать производную функции в точке $x_0$: $y’(2) = 2 x = 2 cdot 2= 4$.

Все полученные значения расставляем по своим местам в формулу $(1)$:

$y-4=-frac{1}{4} cdot (x – 2)$

Уравнение нормали найдено.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 07.05.2023

Прежде чем перейти к изучению функции «y = kx»
внимательно изучите урок
«Что такое функция в математике»
и
«Как решать задачи на функцию».

Другими словами, можно сказать, что «y = kx + b» — это семейство всевозможных функций, где вместо
«k» и «b» стоят числа.

Примеры функций типа «y = kx + b».

• y = 5x + 3
• y = −x + 1
• y = x − 2
• y = 0,5x

Давайте определим для каждой функций выше, чему равны числовые коэффициенты
«k» и
«b».

Функция	Коэффициент «k»	Коэффициент «b»
y = 5x + 3	k = 5	b = 3
y = −x + 1	k = −1	b = 1
y = 2 3 x − 2	k = 2 3	b = −2
y = 0,5x	k = 0,5	b = 0

Обратите особое внимание на функцию «y = 0,5x»
в таблице. Часто совершают ошибку при поиске в ней числового коэффициента «b».

Рассматривая
функцию «y = 0,5x», неверно утверждать, что числового коэффициента
«b» в функции нет.

Числовый коэффициент «b» присутствет в функции типа «y = kx + b» всегда.
В функции «y = 0,5x»
числовый коэффициент «b» равен нулю.

Как построить график линейной функции
«y = kx + b»

Так как графиком функции «y = kx + b»
является прямая линия, функцию называют линейной функцией.

Из геометрии вспомним аксиому (утверждение, которое не требует доказательств),
что через любые две точки можно провести прямую и притом только одну.

Исходя из аксиомы выше следует, что
чтобы построить график функции вида
«у = kx + b» нам достаточно будет найти всего
две точки.

Для примера построим график функции «y = −2x + 1».

Найдем значение функции «y» для двух произвольных значений «x».
Подставим, например, вместо «x» числа «0» и «1».

x	Расчет «y = −2x + 1»
0	y(0) = −2 · 0 + 1 = 1
1	y(1) = −2 · 1 + 1 = −2 + 1 = −1

Полученные значения «x» и «y» — это координаты точек графика функции.

Запишем полученные координаты точек «y = −2x + 1» в таблицу.

Точка	Координата по оси «Оx» (абсцисса)	Координата по оси «Оy» (ордината)
(·)A	0	1
(·)B	1	−1

Отметим полученные точки на системе координат.

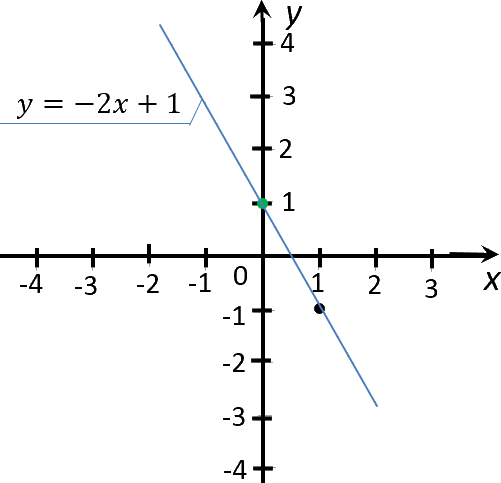
Теперь проведем прямую через отмеченные точки. Эта прямая будет
являться графиком функции «y = −2x + 1».

Как решать задачи на
линейную функцию «y = kx + b»

Рассмотрим задачу.

---

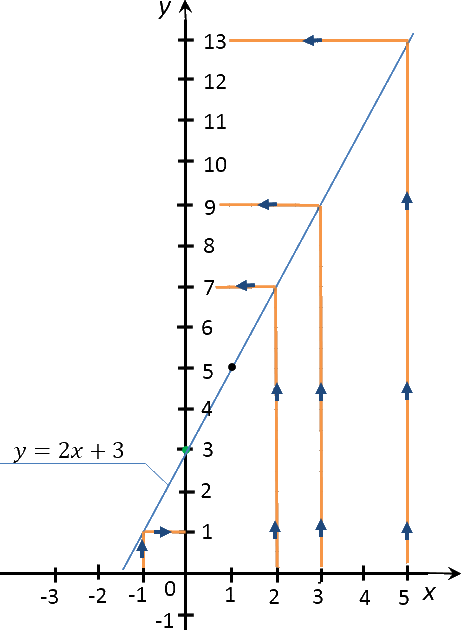
Построить график функции «y = 2x + 3». Найти по графику:

1. значение «y» соответствующее значению «x» равному −1; 2; 3; 5;
2. значение «x», если значение «y» равно
   1; 4; 0; −1.

---

Вначале построим график функции «y = 2x + 3».

Используем правила, по которым мы строили график функции выше.
Для построения графика функции «y = 2x + 3» достаточно найти всего две точки.

Выберем два произвольных числовых значения для «x». Для удобства расчетов выберем числа
«0» и «1».

Выполним расчеты и запишем их результаты в таблицу.

Точка	Координата по оси «Оx»	Координата по оси «Оy»
(·)A	0	y(0) = 2 · 0 + 3 = 3
(·)B	1	y(1) = 2 ·1 + 3 = 5

Отметим полученные точки на прямоугольной системе координат.

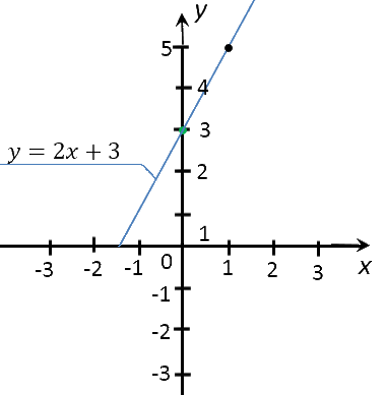
Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции
«y = 2x + 3».

---

Теперь работаем с построенным графиком функции «y = 2x + 3».

Требуется найти значение «y»,
соответствующее значению «x»,
которое равно −1; 2; 3; 5.

---

Тему
«Как получить координаты точки функции» с графика функции
мы уже подробно рассматривали в уроке
«Как решать задачи на функцию».

В этому уроке для решения задачи выше вспомним только основные моменты.

По правилам выше найдем на построенном ранее графике функции «y = 2x + 3»
необходимые значения функции «y» для
«x» равным −1; 2; 3; 5.

Запишем полученные результаты в таблицу.

Заданное значение «x»	Полученное с графика значение «y»
−1	1
2	7
3	9
5	13

---

Переходим ко второму заданию задачи. Требуется найти значение «x»,
если значение «y» равно 1; 4; 0; −1.

Выполним те же действия, что и при решении предыдущего задания.
Разница будет лишь в том, что изначально мы будем проводить перпендикуляры от оси
«Oy».

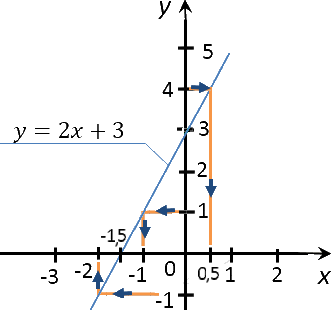
Запишем полученные результаты в таблицу.

Заданное значение «y»	Полученное с графика значение «x»
−1	−2
0	−1,5
1	−1
4	0,5

---

Как проверить, проходит ли график через точку

Рассмотрим другое задание.

Не выполняя построения графика функции
«y = 2x −
», выяснить, проходит ли график
через точки с координатами (0;
− ) и (1; −2).

---

Подставим в функцию
«y = 2x −
»

координаты точки (0;
− ).

− = 2 · 0
−

   − =
−

(верно)

Это означает, что график функции «y = 2x −
» проходит через точку с координатами (0;
− ).

---

Проверим точку с координатами (1; −2).
Также подставим координаты
в функцию «y = 2x −
».

−2 = 2 · 1 −

−2 = 2 −

−2 = 1 −

        −2 = 1 (неверно)

Это означает, что график функции «y = 2x −
» не проходит через точку с координатами (1; −2).

---

Как найти точки пересечения графика с осями

Рассмотрим задачу.

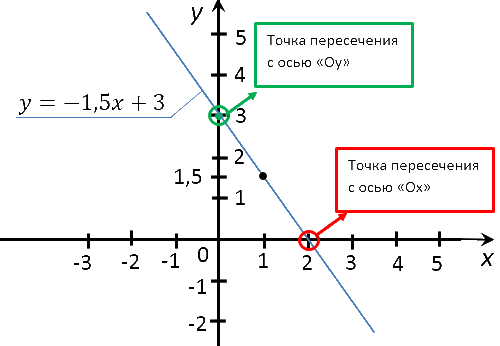
Найти координаты точек пересечения графика функции «y = −1,5x + 3» с осями координат.

Для начала построим график функции «y = −1,5x + 3» и на графике отметим точки пересечения
с осями.

Для построения графика функции найдем координаты двух точек
функции
«y = −1,5x + 3».

Выберем два произвольных числовых значения для «x» и рассчитаем значение
«y» по формуле
функции. Например, для x = 0 и
x = 1.

Точка	Координата по оси «Оx»	Координата по оси «Оy»
(·)A	0	y(0) = −1,5 · 0 + 3 = 3
(·)B	1	y(1) = −1,5 · 1 + 3 = 1,5

Отметим полученные точки на системе координат и проведем через них прямую.
Тем самым мы построим график функции «y = −1,5x + 3».

Теперь найдем координаты точек пересечения графика функции с осями по формуле функции.

Подставим вместо «x» в формулу функции «y = −1,5x + 3» число ноль.

y(0) = −1,5 · 0 + 3 = 3

(0; 3) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Oy».

Подставим вместо «y» в формулу функции «y = −1,5x + 3» число ноль.

0 = −1,5x + 3        
1,5x = 3        | :(1,5)
x = 3 : 1,5           
x = 2                   

(2; 0) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Ox».

Чтобы было проще запомнить, какую координату точки нужно приравнивать к нулю, запомните
«правило противоположности».

---

Ваши комментарии

Оставить комментарий:

---

Здравствуйте!   Подскажите, пожалуйста, как построить перпендикуляр от точки пересечения двух линейных графиков на ось Х.  Тупо рисую вручную линию, а очень хочется сделать это по-человечачьи, автоматизированными средствами.     И еще. НЕобходимо построить диаграмму на двух осях Х. В форуме уже есть информация на эту тему (выделить диаграмму и в Параметрах во вкладке Оси выбрать вспомогательную ось х. Но у меня не появляется во вкладке Оси опция «вспомогательная ось Х». есть только основная. Что делаю не так? Вроде «соблюла» инструкцию дотошно…?     Заранее спасибо!

	Выберите ряды данных, которые нужно отобразить на вспомогательной оси.     В меню Формат выберите команду Выделенный ряд, а затем — вкладку Ось.     Выберите вариант По вспомогательной оси. (Взято из справки Excel)

Если вопрос не заключался в том, чтобы изменить Оси графика, а имено в том, чтобы построить поверх графика вертикальную прямую от точки пересечения двух линейных графиков до оси, то     — в режиме рисования выбираем построение прямых   — ставим курсор на точку пересечения графиков   — нажимаем Shift и удерживаем его нажатым   — тянем курсор до нужной оси и отпускаем когда рисуемая прямая будет такой, какой она нужна.     При нажатом Shift наклон рисуемой прямой становится дискретным (с шагом в 15 градусов) и легко можно построить вертикальную или горизонтальную прямую.     Но найти точное расположение точки пересечения линий графиков в режиме рисования врятли получится, КМК. Это не AutoCad.

ytk5kyky Пользователь Сообщений: 2410 Регистрация: 01.01.1970

И вопрос был не в том, как нарисовать вертикальную линию, а в том, чтобы ее не рисовать, а отобразить средствами диаграммы.   Татьяна, сперва нужно решить систему с двумя уравнениями, т.е. найти точку пересечения. Я думаю, что самих уравнений у Вас нет. Есть только ряды. Уравнения можно получить, построив линии тренда. Здесь уже были решения по автоматизированному получению из линий тренда формулы в ячейку. Потом, хоть «поиском решения» находим нужную точку на оси Х, а построение ряда по ней — уже дело техники.

	Ок, спасибо за ответы. Буду пробовать построить систему уравнений. Потом опять пристану.

слэн Пользователь Сообщений: 5192 Регистрация: 16.01.2013

если графики линейные, то есть такая формула линейн — находит наклон и y-пересечение прямой     таким образом координаты пересечения графиков будет вычисляться по формулам:   x=(b2-b1)/(a1-a2)   y=a1*x+b1     где а и b, соответственно, наклон и y-пересечение     соответственно, табличка для отображения будет такой:      x     y    x     0   добавьте этот ряд к Вашей диаграмме(диаграмма должна быть точечной)

{quote}{login=}{date=27.11.2008 02:15}{thema=}{post}Выберите ряды данных, которые нужно отобразить на вспомогательной оси.     В меню Формат выберите команду Выделенный ряд, а затем — вкладку Ось.     Выберите вариант По вспомогательной оси. (Взято из справки Excel){/post}{/quote}     Это понятно. Этот путь я знаю. Но он предлагает только ось Y и выжать из него ось Х не получается. Не пойму почему.

{quote}{login=слэн}{date=27.11.2008 11:09}{thema=}{post}если графики линейные, то есть такая формула линейн — находит наклон и y-пересечение прямой     таким образом координаты пересечения графиков будет вычисляться по формулам:   x=(b2-b1)/(a1-a2)   y=a1*x+b1     где а и b, соответственно, наклон и y-пересечение     соответственно, табличка для отображения будет такой:      x     y    x     0   добавьте этот ряд к Вашей диаграмме(диаграмма должна быть точечной){/post}{/quote}   Слэн, спасибо!

Татьяна Гость	#9 29.11.2008 21:22:25 Люди, помогите!   Туплю не по-детски. Вроде все сделала — уравнения задала (взяла пока простой пример, не из жизни, чтобы метод отработать), точки построила, тип диаграммы установила точечный, как опустить этот перпендикуляр? Помогите! Прикрепленные файлы post_40735.xls (24.5 КБ)

Did this article help you?