1.
ABCD — ромб со стороной 4 см. угол ADC 150.
ABCD — ромб со стороной 4 см. угол ADC 150. BM-перпендикуляр к плоскости ромба и равен 2 корня из 3. найдите расстояние от точки M до AD. ОБЯЗАТЕЛЬНО НУЖЕН РИСУНОК!

Светило науки — 549480 ответов — 388270 раз оказано помощи
по условию сделаем рисунок
опустим из вершины B перпендикуляр к AD пересечение точка М1
по теореме о трех перпендикулярах
BM1 — проекция наклонной MM1 и тогда MM1 перпендикулярна AD
Перпендикуляр ММ1 — это искомое расстояние
по условию сторона AB = 4 см
<A = 180 — <ADC — односторонние
< A = 180 — 150 =30
тогда
в прямоугольном треугольнике ABM1
BM1 = AB*sinA = 4*sin30 = 2 см
по условию BM = 2√3
по формуле Пифагора
MM1^2 = BM1^2 +BM^2
MM1 = √ 2^2 + (2√3)^2 =√ (4 +12) = √16 =4
ответ 4 см

Светило науки — 3 ответа — 0 раз оказано помощи
Опустим точку в в сторону AD перпедикулятор Вк
так как угол DABравен ( 360-150-150)/2 =30 градусов.
то вк=1/2 ав =2 см
искаемое рстояние равно км
км ^2=2^2+(2*3^(1/2))^2 = 16 отсюда км равен 4 см
Задача 13240 AM — Пендикуляр к плоскости ромба ABCD…
Условие
AM — Пендикуляр к плоскости ромба ABCD Длиной 8 см. Известно, что расстояние от точки М до прямой НС равно 10 см, угол В = 20°. Выполните дополнительное построения и найдите растояние oт точки М до прямой BD.
1) 12 см
2) 10 см
3) 10,5 см
4) 14 см
АВС — равнобедренный треугольник. ВС = АС =10 см, АВ = 12 см. Точка S удалена от каждой стороны на 15 см. Найдите расстояние от точки S до плоскости треугольника.
1) 8 см
2) 6sqrt(6) см
3) 12 см
4) 8sqrt(3) см

математика 10-11 класс
12739
Решение
★
1)
МК⊥ВС
По теореме о трех перпендикулярах АК⊥ВС.
Из прямоугольного треугольника АМК
АМ^2=MK^2-MA^2=10^2-8^2=100-64=36
AM=6
Из прямоугольного треугольника АКВ(∠АВК=180 градусов -120 градусов=60 градусов)
АВ=АК/sin60 градусов=6/(sqrt(3)/2)=4sqrt(3).
Проводим диагональ АС. Диагонали ромба взаимно перпендикулярны и в точке пересечения делятся пополам. Диагонали ромба являются биссектрисами углов ромба.
Поэтому в прямоугольном треугольнике АОВ
АО=АВ*sin60 градусов=4sqrt(3)*(sqrt(3)/2)=6
Из прямоугольного треугольника МАО
МО^2=MA^2+AO^2=8^2+6^2=100
МО=10
(Можно доказать, что треугольники АКВ и АОВ;
МАК и МАО равны)
2) Равные наклонные имеют равные проекции.
Поэтому ОМ=ОК=ON=r ( радиусу вписанной окружности)
r=S/p
Проводим высоту равнобедренного треугольника СМ.
Она является и медианой.
Из прямоугольного треугольника АСМ
СМ^2=AC^2-MA^2=10^2-6^2=100-36=64
CМ=8 см.
S(Δ ABC)=АВ*СМ/2=8*12/2=48 кв см.
р=(10+10+12)/2=16
r=48/16=3
По теореме Пифагора
SO^2=SM^2-MO^2=15^2-3^2=225-9=216
SO=sqrt(216)=6sqrt(6)
О т в е т. 6 sqrt(6)
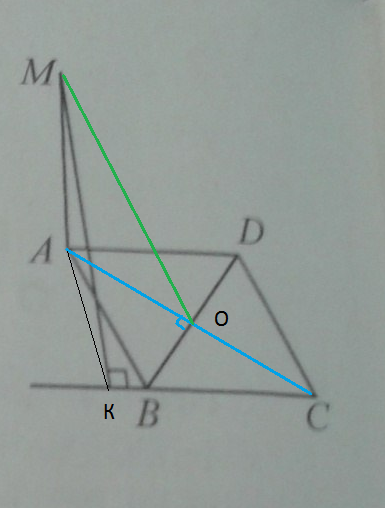
Написать комментарий
Светило науки — 7309 ответов — 165986 раз оказано помощи
а) По определению проекция фигуры на плоскость — совокупность проекций всех точек этой фигуры на плоскость проекции.
Точка К проецируется в основание перпендикуляра КА, т.е. в т. А.
Т. В и С ∆ КВС лежат в плоскости ромба. Через две точки можно провести только одну прямую. ⇒
Все точки сторон ∆ КВС проецируются на стороны ∆ АВС. ⇒
∆ АВС проекция ∆ КВС на плоскость ромба АВCД.
б) КА перпендикулярен плоскости ромба, следовательно, перпендикулярен любой прямой, проходящей в этой плоскости через т. А. ⇒КА⊥АС
Диагонали ромба взаимно перпендикулярны.⇒АС⊥ВД
АО — высота равнобедренного ∆ АВД. Из ∆ АОВ по т.Пифагора АО=√(B²-BO²)=√(25-9)=4
Расстояние от точки до прямой равно длине проведенного между ними перпендикуляра.
КО по т. о 3-х перпендикулярах перпендикулярен ВД.
Из прямоугольного ∆ КАО расстояние КО=√(КА²+АО*)=√(9+16)=5 см

1. По условию задачи известно, что что сторона ромба abcd равна 5 cм, одна диагональ
bd = 6 см, из вершины а проведен перпендикуляр к плоскости ромба ка = 3 см.
2. Знаем, что расстояние от от точки до прямой измеряется длиной перпендикуляра, значит
и его проекция должна быть перпендикулярна к прямой bd.
А в ромбе диагонали в точке пересечения О взаимно перпендикулярны, значит проекцией является отрезок аО, равный половине диагонали ас.
3. Вычислим чему равен ао в прямоугольном треугольнике аОв по теореме Пифагора:
аО² = ав² — вО², откуда аО = √5² — (6/2)² = √25 — 9 = 4 см.
4. Определим длину кО тоже по теореме:
кО² = ак² + аО², и значит кО = √4² + 3² = √16 + 9 = 5 см.
Ответ: Расстояние равно 5 см.
Итоговая контрольная работа по геометрии за 10 класс (средний уровень) с ответами и решениями по УМК Атанасян . Урок 66 поурочного планирования по геометрии (автор: Яровенко В.А.). Геометрия 10 Атанасян КР-6 Уровень 2 (средний). Цитаты использованы в учебных целях.
Смотреть Список всех контрольных по геометрии в 7 классе по УМК Атанасян.
Другие уровни сложности итоговой работы:
К6 Уровень 1 (легкий) + Решения
К6 Уровень 3 (сложный) + Решения
Итоговая контрольная работа по геометрии за 10 класс (средний уровень)
КР-6 У2. Вариант 1 (транскрипт заданий)
- Диагонали ромба ABCD пересекаются в точке О. SA — перпендикуляр к плоскости ромба. SA = 3√3 см, АС = 6 см.
а) Докажите, что прямая BD перпендикулярна к плоскости SAO;
б) Найдите | SD + 1/2 (DA + DC) |;
в) Найдите двугранный угол SDBA. - В правильной треугольной пирамиде плоский угол при вершине равен 120°. Отрезок, соединяющий основание высоты пирамиды с серединой бокового ребра, равен 3 см. Найдите площадь полной поверхности пирамиды.
- Постройте сечение правильного тетраэдра DABC, проходящего через середины ребер AD и ВС параллельно ребру DB.
КР-6 У2. Вариант 2 (транскрипт заданий)
- Диагонали ромба ABCD пересекаются в точке О. SA — перпендикуляр к плоскости ромба SO = 6 см, АВ = 5 см, BD = 8 см.
а) Докажите, перпендикулярность плоскостей SBD и SAO;
б) Найдите | 1/2 (AD+AB)+OS |;
в) Найдите угол между прямой SO и плоскостью АВС. - В правильной треугольной пирамиде двугранный угол при основании равен 60°. Отрезок, соединяющий основание высоты пирамиды с серединой апофемы, равен 3 см. Найдите площадь полной поверхности пирамиды.
- Постройте сечение правильного тетраэдра DABC, проходящего через середины ребер AD и АВ параллельно ребру АС.
Геометрия 10 Атанасян КР-6 Уровень 2.
Решения и ответы (средний уровень):
КР-6 У2. Ответы на Вариант 1
Смотреть РЕШЕНИЯ заданий Варианта 1
КР-6 У2. Ответы на Вариант 2
Смотреть РЕШЕНИЯ заданий Варианта 2
Другие уровни сложности итоговой работы:
К6 Уровень 1 (легкий) + Решения
К6 Уровень 3 (сложный) + Решения
Вы смотрели: Итоговая контрольная работа по геометрии в 10 классе с ответами для УМК Атанасян Просвещение. Урок 66 поурочного планирования по геометрии. Геометрия 10 Атанасян КР-6 Уровень 2 (средний).
Смотреть Список всех контрольных по геометрии в 10 классе по УМК Атанасян.

