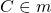Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Серединный перпендикуляр к отрезку
Определение 1. Серединным перпендикуляром к отрезку называется прямая, которая проходит через середину отрезка и перпендикулярная к нему.
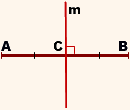
На рисунке 1 прямая ( small l ) серединный перпендикуляр к отрезку ( small AB .)
Теорема о серединном перпендикуляре к отрезку
Теорема 1. 1) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. 2) Обратно: Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Доказательство. 1) Пусть точка ( small O ) середина отрезка ( small AB ) и пусть прямая ( small q ) серединный перпендикуляр к отрезку ( small AB ) (Рис.2). Рассмотрим любую точку ( small M ) на прямой ( small q ). Докажем, что ( small AM=BM. ) Если точка ( small M ) совпадает с точкой ( small O ), то равенство ( small AM=BM ) верно поскольку ( small AO=BO ) (( small O )-середина отрезка). Пусть ( small M ) и ( small O ) различные точки. Тогда прямоугольные треугольники ( small MOA ) и ( small MOB ) равны по двум катетам (( small AO=OB ), ( small OM )− общий). Следовательно ( small AM=BM. )
2) Пусть точка ( small P ) равноудалена от от концов отрезка ( small AB ) (Рис.3). Тогда выполено равенство ( small AP=BP ). Докажем, что ( small P ) лежит на серединном перпендикуляре ( q ). Если точка ( small P ) принадлежит прямой ( small AB ), то поскольку она равноудалена от концов отрезка ( small AB, ) она совпадает с точкой ( small O ), т.е. лежит на прямой ( q.) Если же ( small P ) не лежит на прямой ( small AB ), то треугольник ( small ABP ) равнобедренный, поскольку ( small AP=BP .) Отрезок ( small PO ) медиана этого равнобедренного треугольника и, значит, является также высотой этого треугольника. Тогда ( small PO⊥AB .) Прямые ( small PO ) и ( q ) проходят через точку ( small O ) и перпендикулярны к ( small AB .) Следовательно эти прямые совпадают, т.е. точка ( small P ) принадлежит прямой ( q. )
Серединный перпендикуляр
Что такое серединный перпендикуляр к отрезку? Что можно сказать о пересечении серединных перпендикуляров к сторонам треугольника? К сторонам многоугольника?
Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.
m — серединный перпендикуляр к отрезку AB, если
точка C — середина отрезка AB,
Чтобы построить серединный перпендикуляр к данному отрезку с помощью угольника, нужно:
1) найти середину отрезка;
2) провести через эту точку прямую, перпендикулярную данному отрезку (для этого угольник прикладываем прямым углом к середине отрезка так, чтобы она сторона угольника проходила через отрезок, а через другую сторону проводим прямую):
Свойства серединного перпендикуляра.
1) Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.
Например, прямая m — геометрическое место точек, равноудаленных от точек A и B (рисунок 1).
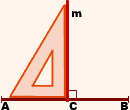
2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Эта точка является центром описанной около треугольника окружности.
3) Если около многоугольника можно описать окружность, то центр этой описанной окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
http://matworld.ru/geometry/seredinnyj-perpendikulyar.php
Решить треугольник Онлайн по координатам
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Загрузить PDF
Загрузить PDF
Серединный перпендикуляр — это прямая, перпендикулярная отрезку и делящая его пополам. Чтобы найти серединный перпендикуляр отрезка по его двум точкам, нужно найти точку, являющуюся серединой отрезка, и угловой коэффициент перпендикуляра и подставить найденные значения в линейное уравнение.
-
1
Найдите середину отрезка, ограниченного двумя данными точками. Для этого подставьте координаты точек в формулу: [(x1 + x2)/2,( y1 + y2)/2]. Эта формула вычислит среднее значение координат х и у двух данных точек. Например, даны следующие координаты двух точек: (x1,y1)=(2,5) и (x2,y2)=(8,3). [1]
- [(2+8)/2, (5 +3)/2] =
- (10/2, 8/2) =
- (5, 4)
- Координаты середины отрезка, ограниченного точками с координатами (2,5) и (8,3), есть (5,4).
-
2
Найдите наклон прямой (угловой коэффициент). Чтобы найти угловой коэффициент по двум точкам, подставьте их координаты в формулу: (y2 — y1) / (x2 — x1). Угловой коэффициент равен тангенсу угла между положительным направлением оси абсцисс и данной прямой. Вот как найти угловой коэффициент прямой, которая проходит через точки (2,5) и (8,3): [2]
- (3-5)/(8-2) =
- -2/6 =
- -1/3
- Угловой коэффициент прямой равен -1/3. Для получения этого результата мы сократили дробь 2/6.
-
3
Найдите угловой коэффициент перпендикуляра. Для этого найдите обратную величину углового коэффициента прямой и измените знак. Для получения обратной величины разделите единицу на данную величину.[3]
- Обратная отрицательная величина -1/3 есть 3, потому что 1/(1/3)=3, а знак был изменен с отрицательного на положительный.
Реклама
-
1
Линейное уравнение записывается в виде: y = mx + b, где х и у — координаты, m – угловой коэффициент, b – смещение прямой по оси Y.[4]
-
2
Подставьте в уравнение найденный угловой коэффициент перпендикуляра. Подставьте 3 вместо m:
- 3 —> y = mx + b =
- y = 3x + b
-
3
Подставьте координаты середины отрезка. Это точка с координатами (5,4). Поскольку перпендикуляр проходит через эту точку, подставьте ее координаты в линейное уравнение. Просто подставьте (5,4) вместо х и у.
- (5, 4) —> y = 3x + b =
- 4 = 3(5) + b =
- 4 = 15 + b
-
4
Найдите смещение по оси Y. Для этого обособьте «b» на одной стороне уравнения.
- 4 = 15 + b =
- -11 = b
- b = -11
-
5
Напишите уравнение, описывающее серединный перпендикуляр. Для этого подставьте значения углового коэффициента (3) и смещения по оси Y (-11) в линейное уравнение. Вы не должны подставлять никаких значений вместо х и у, так как это уравнение позволит вам найти координаты любой точки, лежащей на перпендикуляре.
- y = mx + b
- y = 3x — 11
- Уравнение, описывающее серединный перпендикуляр, проходящий через отрезок, ограниченный точками с координатами (2,5) и (8,3), записывается как у=3x-11.
Реклама
Об этой статье
Эту страницу просматривали 32 613 раз.
Была ли эта статья полезной?
Серединный перпендикуляр
Что такое серединный перпендикуляр к отрезку? Что можно сказать о пересечении серединных перпендикуляров к сторонам треугольника? К сторонам многоугольника?
Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.
m — серединный перпендикуляр к отрезку AB, если
точка C — середина отрезка AB,
Чтобы построить серединный перпендикуляр к данному отрезку с помощью угольника, нужно:
1) найти середину отрезка;
2) провести через эту точку прямую, перпендикулярную данному отрезку (для этого угольник прикладываем прямым углом к середине отрезка так, чтобы она сторона угольника проходила через отрезок, а через другую сторону проводим прямую):
Свойства серединного перпендикуляра.
1) Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.
Например, прямая m — геометрическое место точек, равноудаленных от точек A и B (рисунок 1).
2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Эта точка является центром описанной около треугольника окружности.
3) Если около многоугольника можно описать окружность, то центр этой описанной окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
Серединные перпендикуляры к сторонам треугольника
Теорема 1. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Доказательство. Пусть ( small m ) и ( small n ) серединные перпендикуляры сторон ( small AB ) и ( small BC ) треугольника ( small ABC, ) соответственно (Рис.1). Покажем, сначала, что они пересекаются. Предположим, что ( small m ) и ( small n ) параллельны. Тогда прямая ( small AB, ) которая перпендикулярна к прямой ( small m, ) перпендикулярна и к прямой ( small n.) Получается, что через точку ( small B ) проходят две прямые ( small AB ) и ( small BC, ) которые перпендикулярны к прямой ( small n. ) Но это невозможно. Следовательно прямые ( small m ) и ( small n ) пересекаются в некоторой точке ( small O. )
Поскольку точка ( small O ) находится на серединном перпендикуляре к отрезку ( small AB ,) то равноудалена от точек ( small A ) и ( small B. ) Тогда ( small AO=BO. ) Аналогично ( small BO=CO. ) Следовательно ( small AO=CO, ) то есть точка ( small O ) находится на серединном перпендикуляре отрезка ( small AC. ) Получили, что все три серединных перпендикуляра ( small m, n, p ) пересекаются в точке ( small O. )
Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов
Серединный перпендикуляр к отрезку
Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).
Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.
Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .
Докажем, что отрезок AE длиннее отрезка EB . Действительно,
Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.
Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,
Полученное противоречие и завершает доказательство теоремы 2
Окружность, описанная около треугольника
Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .
Свойства описанной около треугольника окружности. Теорема синусов
Для любого треугольника справедливы равенства (теорема синусов):

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.
Для любого треугольника справедливо равенство:
где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.
Для любого треугольника справедливо равенство:
где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
| Фигура | Рисунок | Свойство |
| Серединные перпендикуляры к сторонам треугольника |
 |
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство |
| Окружность, описанная около треугольника |  |
Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |
| Центр описанной около прямоугольного треугольника окружности |  |
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство |
| Центр описанной около тупоугольного треугольника окружности |  |
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов |  |
|
| Площадь треугольника |  |
|
| Радиус описанной окружности |  |
| Серединные перпендикуляры к сторонам треугольника |
 |
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Окружность, описанная около треугольника
Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Центр описанной около остроугольного треугольника окружности
Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.
Центр описанной около тупоугольного треугольника окружности
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов
Для любого треугольника справедливы равенства (теорема синусов):

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.
Площадь треугольника
Для любого треугольника справедливо равенство:
где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.
Радиус описанной окружности
Для любого треугольника справедливо равенство:
где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).
Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
При доказательстве теоремы 3 было получено равенство:
из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.
Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).
Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
Формула (1) доказана.
Из формулы (1) для вписанного треугольника ABC получаем (рис.7):
источники:
http://matworld.ru/geometry/seredinny-perpendikulyar-treugolnika.php
http://www.resolventa.ru/spr/planimetry/otcircle.htm

РЕШЕНИЕ ЗАДАЧ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
Задача 1. Определить элементы треугольника, если заданы уравнения трех его сторон:
АС: х – 2у + 5 = 0, АВ: х + 2у – 3 = 0,
ВС: 2х + у – 15 = 0.
Решение
1. Вершины треугольника
Координаты вершин треугольника находятся как точки пересечения соответствующих сторон. Так, например, координаты точки А являются решением системы уравнений
x − 2y +5 = 0,
x + 2y −3 = 0.
Нетрудно показать, что А (-1, 2). Аналогично находим В (9, -3) и С (5, 5).
2. Уравнения высот
Высотой треугольника называется отрезок перпендикуляра, опущенного из вершины треугольника на противоположную сторону.
Так, например, hc = CC1 AB. Уравнение высоты СС1 ищем как уравнение
|
прямой у |
= |
k1x + b, если известен угловой коэффициент прямой АВ: |
|||||
|
y = − |
1 x + |
3 |
, |
равный k2 |
= − |
1 |
. Из условия перпендикулярности прямых k1 k2 |
|
2 |
2 |
2 |
= -1 → k1 = 2. Поскольку высота СС1 проходит через точку (5, 5), уравнение hc имеет вид у – 5 = 2 (х – 5) или у = 2х – 5.
Анализ уравнений сторон АС: y = 12 x + 52 и ВС: у = —2х + 5 убеждает нас в том, что АС ВС, и треугольник является прямоугольным. Таким образом, hA: y = 12 x + 52 ; hB: у = —2х + 15.
3. Уравнения медиан
Медианой называется отрезок прямой, соединяющей вершину треугольника с серединой противолежащей ей стороны.
Координаты середин сторон находятся по формулам деления отрезка в данном отношении (см. п.1.2): С2 (4, -1/2), В2 (2, 7/2), А2 (7, 1).
Уравнение медианы mC = CC2 получается как уравнение прямой, проходящей через точки С и С2 (см. п.2.3):
|
y −5 |
= |
x |
−5 |
или mC: 11х – 2у – 45 = 0. |
|
−1 2 −5 |
−5 |
|||
|
4 |
34

положительно, так как начало координат и
отрицательно, так как начало координат и
Аналогично mВ: —13х – 14у + 75 = 0, mА: -x – 8y + 15 = 0.
4. Длины сторон
По формуле расстояния между двумя точками (см. п.I.I):
AB = c = 102 +52 = 5 5, BC = a = 4 5, AC = b = 3 5.
5. Уравнения биссектрис
Биссектрисой треугольника называется лежащий в треугольнике отрезок прямой, которая делит его внутренний угол пополам.
Укажем два способа нахождения уравнения биссектрисы треугольника.
а). Биссектриса делит противолежащую сторону в отношении, пропорциональном прилежащим сторонам.
Если С3 – точка пересечения биссектрисы lC = CC3 со стороной АС, то
АС3 = АС = b = 3 . С3 В СВ a 4
Координаты точки С3 находим по формулам деления отрезка в данном отношении λ = 3/4 (см. п.1.2): С3 (23/7, -1/7).
Уравнение биссектрисы lC = CC3 получается как уравнение прямой, проходящей через точки С3 и С (5, 5) (см. п.2.3):
|
y −5 |
= |
x −5 |
или 3х – у – 10 = 0. |
|||
|
−1 7 − |
5 |
23 7 − |
5 |
|||
б). Уравнение биссектрисы lC = CC3 может быть найдено из условия того, что точки биссектрисы CC3 равноудалены от сторон АС и СВ.
Вычислим отклонения точки (х, у), лежащей на биссектрисе, от сторон АС
|
и СВ (см. п.2.7): |
||||||
|
δАС = |
x −2y +5 |
, |
δСB = |
2x + y −15 |
; |
|
|
− 5 |
5 |
|||||
δАС и δСВ отрицательны, так как начало координат и точки биссектрисы треугольника лежат по одну сторону от сторон АС и СВ. Учитывая, что d = |δ|, уравнение биссектрисы получим из равенства δ = −δ , δ < 0 ,-δАС = —δСВ,
|
которое принимает вид: |
x − 2y +5 |
= − |
2x + y −15 |
или lC: 3х – у – 10 = 0. |
|
|
5 |
5 |
||||
Для вычисления биссектрисы угла А lА применим второй способ.
Отклонение δАС = − x − 2y +5

биссектриса lА лежат по одну сторону от стороны АС.
Отклонение δAB = x + 2y −3

биссектриса lА лежат по разные стороны от стороны АВ. Для биссектрисы lА справедливо —δАС = δАВ,
35
|
то есть |
x − 2y +5 |
= x + 2y −3 |
или х – 2у + 5 = х + 2у –3. |
|
|
5 |
||||
|
5 |
||||
|
Следовательно, 4у = 8. Таким образом, lА: у = 2. |
Уравнение lВ: х+у – 6 = 0 может быть найдено одним из двух способов.
|
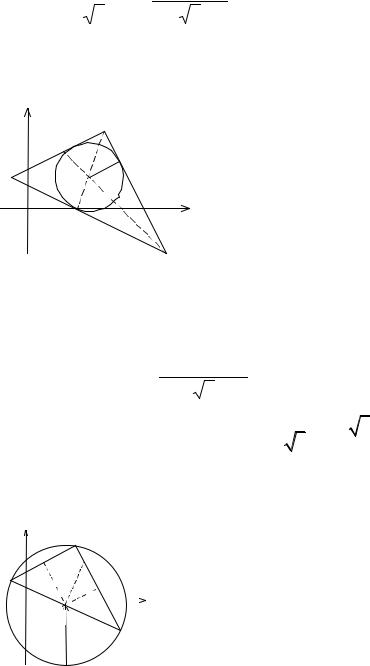
6. Центр и радиус вписанной окружности |
||||||||
|
у |
Биссектрисы треугольника пересекаются в |
|||||||
|
С |
одной точке, являющейся центром вписанной |
|||||||
|
окружности. |
||||||||
|
r |
||||||||
|
А |
Система уравнений, составленная из уравнений |
|||||||
|
01 |
х |
|||||||
|
0 |
биссектрис: |
|||||||
|
3х− у−10 |
= 0, |
|||||||
|
B |
||||||||
|
у = 2, |
имеет решение х = 4, у = 2.
Следовательно, центр вписанной окружности находится в точке О1 (4, 2). Радиус вписанной окружности найдем как расстояние от точки О1 до
|
стороны АС: δ |
АС |
= − x0 −2y0 |
+5 , где х = 4, у = 2. |
|||||||||||||||||||||||||||
|
5 |
0 |
0 |
||||||||||||||||||||||||||||
|
Таким образом, |
r = dAC = |
δAC |
= |
− 4 − 4 +5 |
= |
5. |
||||||||||||||||||||||||
|
5 |
||||||||||||||||||||||||||||||
|
7. Центр и радиус описанной окружности |
||||||||||||||||||||||||||||||
|
Центр описанной |
окружности |
находится |
в |
точке |
пересечения |
|||||||||||||||||||||||||
|
перпендикуляров, |
восстановленных |
к |
сторонам |
|||||||||||||||||||||||||||
|
у |
С |
треугольника в их серединах. |
||||||||||||||||||||||||||||
|
BB2 |
Координаты |
середин |
сторон |
АС |
и |
АВ |
найдены |
|||||||||||||||||||||||
|
А |
2 |
|||||||||||||||||||||||||||||
|
х в п.3). |
С2 (4, -1/2), В2 (2, 7/2). |
|||||||||||||||||||||||||||||
|
A2 |
||||||||||||||||||||||||||||||
|
Уравнения линий серединных перпендикуляров hC |
и hB |
|||||||||||||||||||||||||||||
|
O0 |
O2 |
|||||||||||||||||||||||||||||
|
R |
B |
находим аналогично вычислениям в п.2. |
2 |
2 |
||||||||||||||||||||||||||
|
R |
||||||||||||||||||||||||||||||
|
Угловые |
коэффициенты |
hC |
2 |
и hB |
равны |
2 |
и -2 |
|||||||||||||||||||||||
|
2 |
соответственно, и эти прямые проходят через точки С2 и В2, их уравнения имеют вид:
|
h |
: y + |
1 |
= 2(x −4) |
или 4x −2y −17 = 0, |
||||
|
C2 |
2 |
|||||||
|
h |
: y − |
7 |
= −2(x −4) |
или 4x + 2y −15 = 0. |
||||
|
B |
2 |
|||||||
|
2 |
||||||||
|
Система уравнений, составленная из уравнений серединных |
||||||||
|
перпендикуляров: |
||||||||
|
4x − 2 y −17 = 0, |
, имеет решение х = 4, у = -1/2. |
|||||||
|
0 |
||||||||
|
4x + 2 y −15 |
= |
36

Следовательно, центр описанной окружности находится в точке О2 (4, -1/2). Нетрудно заметить, что центр описанной окружности совпал с серединой
стороны АВ: R = 12 AB = 5 25 .
8. Центр тяжести треугольника Центр тяжести треугольника находится в точке пересечения медиан.
Из п.3 имеем систему уравнений для определения координат центра
11x − 2y − 45 = 0,
тяжести
−13x −14y + 75 = 0.
Система имеет решение х = 4,33, у = 1,3. Следовательно, центр тяжести
|
треугольника находится в точке О3 (4,33; 1,3). |
||||||||||||||||
|
Укажем, что медианы треугольника делятся точкой пересечения в |
||||||||||||||||
|
отношении 2 : 1, считая от вершины. |
||||||||||||||||
|
Таким образом, координаты центра тяжести могут быть найдены как |
||||||||||||||||
|
координаты точки О3, делящей медиану в отношении λ = |
СО3 |
= |
2 |
. |
||||||||||||
|
С С |
2 |
1 |
||||||||||||||
|
3 |
||||||||||||||||
|
Если воспользоваться формулами деления отрезка в данном отношении |
||||||||||||||||
|
(см. п.1.2), то координаты точки: |
||||||||||||||||
|
x |
= |
xC + 2xC |
2 |
= |
5 + 2 4 |
= 4,33; |
y = |
yC + 2yC |
2 |
= |
5 + 2 (−1 2) |
=1,33. |
||||
|
O |
3 |
3 |
O |
3 |
3 |
|||||||||||
|
3 |
3 |
|||||||||||||||
|
9. |
Внутренние углы треугольника |
Внутренние углы треугольника могут быть найдены через угловые коэффициенты прилежащих сторон. Например, внутренний угол при
|
вершине А треугольника tgA = |
kAC − kAB |
= |
1 2 −(−1 2) |
= 4 . |
|||
|
1 |
+ kAC kAB |
||||||
|
1+1 2 (−1 2) 3 |
Следовательно, А = arctg(4/3). 10. Площадь треугольника
По формуле площади треугольника (см. п.1.3) имеем
|
S∆ = |
1 |
−1 |
2 |
1 |
1 |
|||||||
|
9 −3 |
1 |
= |
60 = 30 (кв. ед.). |
|||||||||
|
2 |
5 |
5 |
1 |
2 |
||||||||
|
Площадь треугольника может быть вычислена по формуле |
||||||||||||
|
S∆ = p r, |
где p – полупериметр треугольника; |
|||||||||||
|
r – радиус вписанной окружности. |
||||||||||||
|
Поскольку p = |
3 |
5 +5 |
5 + 4 5 |
= 6 5, a r = 5, то S∆ =30 (кв. ед.). |
||||||||
|
5 |
||||||||||||
|
Задача 2. Найти точки пересечения следующих линий: |
||||||||||||
|
2.1. (x – 1)2 + (y – 3)2 = 4 |
и (x – 3)2 + (y – 5)2 = 4; |
37

|
2.2. (x – 5)2 + y2 = 1 |
и x + y = 0. |
|||||||||||||
|
Решение |
||||||||||||||
|
1. x2 |
+ y2 |
− 2x − 6y + 6 = 0, |
вычитая из первого уравнения второе, |
|||||||||||
|
x2 |
+ y2 |
−6x −10y |
+30 = 0, |
|||||||||||
|
2 |
+ y |
2 |
− 2x − 6y + 6 = 0, |
|||||||||||
|
получим систему x |
||||||||||||||
|
y = −x + 6, |
||||||||||||||
|
решая которую, получаем две точки пересечения (1, 5) и (3, 3). |
||||||||||||||
|
2.2. Линии |
(x – 5)2 |
+ y2 |
= 1 и x + y = 0 не пересекаются, так как система |
|||||||||||
|
2 |
2 |
|||||||||||||
|
уравнений (х−5) |
+ |
у |
=1, не имеет действительных решений. |
|||||||||||
|
х+ у = 0 |
Задача 3. Найти проекцию точки Р (4, 9) на прямую, проходящую через точки
А (3, 1) и В (5, 2).
Решение
Искомую точку найдем, решая совместно уравнение прямой АВ с уравнением перпендикуляра, проведенного к этой прямой из точки Р.
|
АВ: |
х−3 |
= |
у −1 |
→ у = |
1 |
х− |
1 |
. |
|||||||||
|
1 |
2 |
2 |
|||||||||||||||
|
2 |
|||||||||||||||||
|
Уравнение |
перпендикуляра |
из |
точки Р на прямую АВ |
ищем в виде |
|||||||||||||
|
у – 9 = k(x – 4); из условия перпендикулярности k |
1 |
= −1 |
→ k |
= −2. |
|||||||||||||
|
1 |
1 |
2 |
|||||||||||||||
|
x − |
, |
x = 7, |
|||||||||||||||
|
y = |
2 |
2 |
→ |
||||||||||||||
|
y = 3. |
|||||||||||||||||
|
y = −2x +17, |
Задача 4. Постройте прямую 3х – 5у + 15 = 0.
Решение
Уравнение прямой в отрезках имеет вид: −x5 + 3y =1,
прямая отсекает на осях отрезки (-5) и 3.
Задача 5. Даны две прямые 2х + 3у – 5 = 0, 7х +15у +1 = 0, пересекающиеся в точке М. Составить уравнение прямой, которая проходит через точку М и перпендикулярна к прямой 12х – 5у – 1 = 0.
Решение
Прямые пересекаются, так как угловые коэффициенты 2/7 ≠ 3/15. Составим уравнение пучка прямых с центром в точке М (см. п.2.11):
2х + 3у – 5 + λ (7х + 15у +1) = 0.
38

Чтобы выделить в этом пучке искомую прямую, найдем ее из условия перпендикулярности к прямой 12х – 5у – 1, для которой k1 = 12/5.
|
Из уравнения пучка прямых |
(2 + 7λ) х + (3 + 15λ) у + (-5 + λ) = 0 получаем |
|||||||||
|
k = − |
2 + 7λ |
= − |
1 |
, значит, − |
2 + 7λ |
= − |
5 |
, откуда λ = -1 и уравнение искомой |
||
|
3 +15λ |
k |
3 +15λ |
12 |
|||||||
|
1 |
прямой:
5х + 12у + 6 = 0.
Задача 6. Написать уравнение прямой L, проходящей через точку М (2, 1) под углом 45° к прямой L1: 2х + 3у +4 = 0.
Решение
Угол между прямыми найдем из выражения для тангенса угла α между
|
ними (см. п.2.9): |
||||||
|
tgα = |
k + 2 3 |
=1, где k – угловой коэффициент искомой прямой. |
||||
|
1 |
−(2 3) k |
|||||
Из этого уравнения k1 = 1/5, k2 = -5.
Используя координаты точки М, запишем уравнения искомых прямых:
|
1 |
3 |
x −5y +3 = 0, |
||||
|
L : y = |
5 x + |
5 |
, |
или |
||
|
5x + y −11 = 0. |
||||||
|
y = −5x +11 |
|
Задача |
7. |
Составить |
|
L1: х + 2у – 1 = 0 и L2: х + |
||
|
1 |
y |
|
|
L |
||
|
L |
x |
|
|
2 |
0 |
|
|
L |
||
|
M(x,y) |
||
|
Решение |
уравнение прямой L, параллельной прямым 2у +2 = 0 и проходящей посередине между ними.
1 способ. Уравнение прямой L будем искать в виде А(х – х0) + В(у + у0) = 0. В
|
качестве нормального вектора |
n ={A, B} можно выбрать нормальный вектор |
|
|
прямых |
L1 и L2, равный |
{1, 2}. Найдем какую-нибудь точку |
|
М0 (х0, у0) |
L. Точка М0 будет делить пополам отрезок, соединяющий две |
любые точки, лежащие на L1 и L2. Например, М1 (1, 0) L1 и М2 (-2, 0) L2, тогда точка М0 имеет координаты (-1/2, 0), и уравнение прямой L принимает
вид: х + 2у + 1/2 = 0.
2 способ. Произвольная точка М (х, у) L, если (см. п.2.6)
| δ (М, L1) | = | δ (М, L2) |.
Для снятия модуля определим знаки отклонений точки М (х, у) от прямых L1 и L2. Для этого нужно выяснить взаимное расположение начала координат, точки М (х, у) и прямых L1 и L2.
39

Приведем уравнения прямых к нормальному виду:
|
L1 |
1 |
x + |
2 |
y − |
1 |
n1 |
1 |
2 |
||||||||||||
|
: |
= 0, |
= |
, |
, |
||||||||||||||||
|
5 |
5 |
5 |
5 |
5 |
||||||||||||||||
|
L2 |
: − |
1 |
x − |
2 |
y − |
1 |
= 0, |
n2 |
−1 |
, |
−2 |
, |
||||||||
|
= |
||||||||||||||||||||
|
5 |
5 |
5 |
5 |
5 |
||||||||||||||||
где n1 и n2 — единичные векторы нормалей к прямым L1 и L2, проведенным из
начала координат.
Видим, что n1 и n2 противоположны по направлению, значит, начало координат
лежит в полосе между прямыми L1 и L2. Отсюда заключаем, что точка М и начало координат лежат по одну сторону как от прямой L1, так и от прямой L2, значит, отклонения точки М от прямых L1 и L2 имеют один и тот же знак
|
x + 2y −1 |
−x − 2y − 2 |
следует |
||||
|
(отрицательный), тогда из |
= |
|||||
|
5 |
5 |
|||||
|
х + 2у – 1 = -х – 2у – 2 и |
х + 2у + 1/2 = 0. |
Задача 8. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, что малая ось равна 10, а эксцентриситет равен 12/13.
|
Решение |
b = 5, е = 12/13. Поскольку е = с/а и а2 = b2 + c2, то |
||||||||||||||
|
Из условия имеем |
|||||||||||||||
|
2 |
2 |
2 |
2 |
2 |
b2 |
||||||||||
|
a |
= b |
+ е a |
или |
a |
= |
. Подставляя числовые значения, получим |
|||||||||
|
1−e2 |
|||||||||||||||
|
а2 = 169. |
х2 |
у2 |
|||||||||||||
|
Следовательно, уравнение эллипса имеет вид: |
+ |
=1. |
|||||||||||||
|
169 |
25 |
||||||||||||||
Задача 9. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, что его большая ось равна 10, а расстояние между фокусами равно 8.
Решение
Из условия имеем а = 5, с = 4. Вычислим малую полуось b = a2 −c2 = 25 −16 = 3.
Следовательно, уравнение эллипса имеет вид: х2 + у2 =1. 25 9
Задача 10. Фокусы гиперболы совпадают с фокусами эллипса
Составить уравнение гиперболы, если ее эксцентриситет равен 2.
Решение
Из уравнения эллипса находим: aэл.2 = 25, bэл.2 = 9.
сэл.2 = aэл.2 — bэл.2 = 16, сэл. = 4. По условию сгип. = сэл. = с и егип. = с/агип. = 2.
x2 + y2 =1. 25 9
40
|
Таким образом, агип. = с/2 = 2 и bгип.2 = с2 – агип.2 = 16 |
– 4 = 12. |
||||
|
Уравнение искомой гиперболы имеет вид: |
x2 |
− |
y2 |
=1. |
|
|
4 |
12 |
||||
Задача 11. Составить уравнение параболы, если известны ее фокус F(-7, 0) и уравнение директрисы x – 7 = 0.
Решение
Из уравнения директрисы имеем x = —p/2 = 7 или p = -14.
Таким образом, уравнение искомой параболы y2 = -28x.
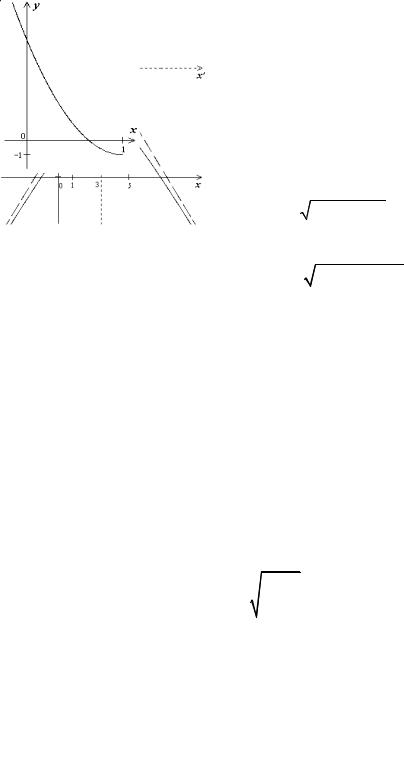
Задача 12. Установить, какие линии определяются следующими уравнениями. Сделать чертежи.
|
1. y = 7 − |
3 |
x2 −6x +13, y < 7, x R. |
||||
|
2 |
||||||
|
Решение |
||||||
|
y −7 = − 3 |
x2 −6x +13. |
Возводим |
обе |
части |
||
|
2 |
||||||
|
уравнения в квадрат: |
||||||
|
(y −7)2 = 94 (x2 −6x +13) |
или |
|||||
|
4 (y −7)2 =(x2 −6x +13). |
||||||
|
9 |
||||||
|
Выделяем в правой части полный квадрат: |
||||||
|
4 (y −7)2 = (x −3)2 + 4 или |
(x −3)2 − ( y −7)2 |
= −1. |
||||
|
9 |
4 |
9 |
Это – сопряженная гипербола. О′(3, 7), полуоси а = 2, b = 3.
Заданное же уравнение определяет ветвь гиперболы, расположенную под прямой y – 7 = 0, т.к. y < 7.
|
2. |
x =1− |
1 |
y +1 |
. |
|
|
2 |
2 |
||||
Решение
Область допустимых значений (х, у) определяется
|
условиями |
||||
|
y +1 |
≥ 0, |
y ≥ −1, |
||
|
→ |
||||
|
2 |
||||
|
− x |
≥ 0, |
x ≤1. |
||
|
1 |
(y + 1)/2 = 4 (1 – x)2 → y + 1 = 8 (1 – x)2.
Искомая кривая – часть параболы с вершиной в точке (1, -1).
41
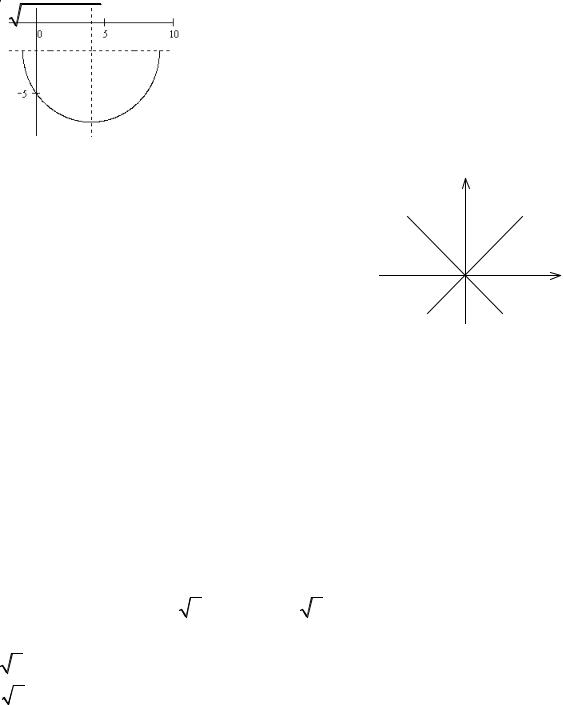
3. y = −2 − 9 − x2 +8x.
Решение
Искомая кривая – часть окружности:
(y + 2)2 + (x – 4)2 = 52, y ≤ -2, x [-1, 9].
|
4. y2 – x2 = 0. |
y |
|||
|
Решение |
||||
|
(y – x) (y + x) = 0 |
y=-x |
y=x |
||
– две пересекающиеся прямые.
x
0
Задача 13. Какую линию определяет уравнение x2 + y2 = x?
Решение
Запишем уравнение в виде x2 – x + y2 = 0.
Выделим полный квадрат из слагаемых, содержащих х: x2 – x = (x – 1/2)2 – 1/4.
|
1 |
2 |
2 |
= |
1 |
|
|
Уравнение принимает вид x − |
2 |
+ y |
4 |
||
и определяет окружность с центром в точке (1/2, 0) и радиусом 1/2.
Задача 14. Преобразовать уравнение x2 – y2 = a2 поворотом осей на 45° против часовой стрелки.
Решение
Так как α = -45°, то cosα = 2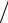
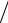
Отсюда преобразование поворота принимает вид (см. п.4.2):
x = 2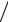
y = 2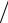
Подстановка в исходное уравнение дает х′у′= а2/2.
Проиллюстрируем приведение общих уравнений прямых второго порядка к каноническому виду на нескольких примерах, иллюстрирующих разные схемы преобразований.
Задача 15. Привести уравнение 5x2 + 9y2 – 30x + 18y + 9 = 0 к каноническому виду и построить кривую.
Решение
Сгруппируем члены этого уравнения, содержащие одноименные
координаты:
(5x2 – 30x) + (9y2 + 18y) +9 = 0, или 5(x2 – 6x) + 9(y2 + 2y) +9 = 0.
42
|
y |
y′ |
Дополняем члены в скобках до полных квадратов: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
5(x2 – 6x + 9 – 9) + 9(y2 + 2y + 1 – 1) +9 = 0, или |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
5(x – 3)2 + 9(y + 1)2 = 45. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x′ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
01 |
Обозначаем x′= x – 3, y′= y + 1, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x0 = 3, y0 = -1, то есть точка О1(3, -1) – центр |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
кривой. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
вид: |
Уравнение в новой системе координат принимает |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
′2 |
y |
′2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
′2 |
+9y |
′2 |
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= |
45 → |
9 |
+ |
5 =1 |
и |
определяет |
эллипс |
с |
полуосями |
|||||||||||||||||||||||||||||||||||||||||||||||
|
5x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
а = 3, b = 5,который в исходной системе координат имеет центр в точке |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
О1(3, -1). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задача 16. Определить вид кривой |
5 x2 |
+ |
3 |
xy |
+ |
7 y2 |
= 2. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Решение |
4 |
4 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Определим угол поворота осей по формуле (7) п.4.4: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A = |
5 |
,C |
7 |
, B = |
3 |
, A ≠ C иϕ= |
1 |
arctg |
2B |
1 |
arctg (− |
3)= − |
π |
|||||||||||||||||||||||||||||||||||||||||||
|
= |
= |
6 . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
4 |
4 |
2 |
A −C |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подвергнем уравнение кривой преобразованию: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
′ |
′ |
′ |
3 |
+ y |
′ |
1 |
, |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
x = x cosϕ− y |
sin ϕ= x |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
′1 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
′ |
′ |
+ y |
′ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
y = x sin ϕ+ y |
cosϕ= −x |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
и получим уравнение эллипса |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
′ |
3 |
+ y |
′1 |
2 |
3 |
′ |
3 |
+ y |
′ |
1 |
1 |
′ |
3 |
′ |
7 |
1 |
′ |
3 |
′ |
2 |
|||||||||||||||||||||||||||||||||||
|
+ |
− |
+ |
− |
= 2 . |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
x |
2 |
2 |
2 |
x |
2 |
2 |
2 |
x + |
2 |
y |
4 |
2 |
x + |
2 |
y |
||||||||||||||||||||||||||||||||||||||||
x′2 + 2y′2 = 2.
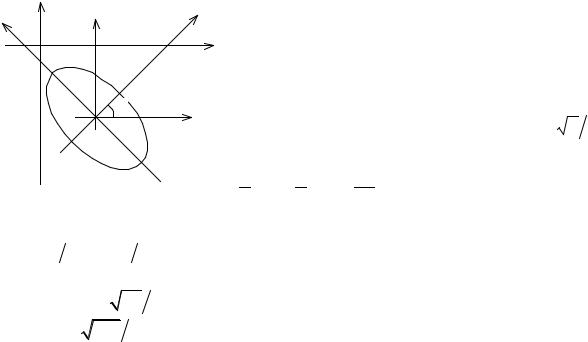
Задача 17. Установить, какую линию определяет уравнение x2 + y2 + xy – 2x + 3y = 0.
Решение
Перенесем начало координат в такую точку О1(х0, у0), чтобы уравнение не содержало х′ и у′ в первой степени.
Это соответствует преобразованию координат вида (см. п.4.1):
x = x′+ x0 ,y = y′+ y0.
Подстановка в исходное уравнение дает
(x′+ x0)2 + (x′+ x0)(y′+ y0) + (y′+ y0)2 – 2(x′+ x0) + 3(y′+ y0) = 0 или
x′2 + x′y′+ y′2 + (2x0 + y0 — 2)x′+ (x0 + 2y0 + 3)y′+ x02 + x0y0 + y02 — 2x0 + 3y0 =0.
Положим 2x0 + y0 – 2 = 0, x0 + 2y0 + 3 = 0.
43
|
Решение полученной системы уравнений: x0 = 7/3 и y0 = -8/3. |
|||||||||||||||
|
Таким образом, координаты нового начала координат O1(7/3, -8/3), а |
|||||||||||||||
|
уравнение принимает вид x′2 + x′y′+ y′2 = 93/25. |
|||||||||||||||
|
Повернем оси координат на такой угол α, чтобы исчез член х′у′. |
|||||||||||||||
|
Подвергнем последнее уравнение преобразованию (см. п.4.2): |
|||||||||||||||
|
x′ = x′′cosα − y′′sin α, |
|||||||||||||||
|
′ |
′′ |
′′ |
cosα |
||||||||||||
|
y |
= x sin α+ y |
||||||||||||||
|
и получим (cos2α + sinα cosα + sin2α) x′′2 |
+ |
||||||||||||||
|
y′′ |
y |
′ |
x′′ |
(cos2α — sin2α) x′′y′′+ |
|||||||||||
|
y |
x |
2 |
2 |
2 |
|||||||||||
|
0 |
+ |
(sin α — sinα cosα + |
cos α) y′′ |
= |
|||||||||||
|
93/25. |
|||||||||||||||
|
Полагая cos2α — sin2α = 0, имеем tg2α = |
1. |
||||||||||||||
|
α |
x′ |
Следовательно, α1,2 = ±45°. |
|||||||||||||
|
01 |
Возьмем α = 45°, cos45° = sin45° = |
2 2. |
|||||||||||||
|
После соответствующих вычислений получаем |
|||||||||||||||
|
3 |
2 |
1 |
2 |
93 |
|||||||||||
|
2 x′′ |
+ |
2 y′′ |
= 25. |
|
′′2 |
y |
′′2 |
||||||
|
Итак, |
x |
+ |
=1 |
|||||
|
62 25 |
186 25 |
|||||||
|
– уравнение эллипса |
||||||||
|
с полуосями a = |
62 5 ≈1,5; |
|||||||
|
b = |
186 5 ≈ 2,7 |
в дважды штрихованной системе координат, получаемой из исходной параллельным переносом осей координат в точку О1(7/3, -8/3) и последующим поворотом на угол 45° против часовой стрелки.
|
Уравнение x2 + y2 + xy – 2x + 3y = 0 приведено к каноническому виду |
|||||
|
′′2 |
y |
′′2 |
|||
|
x |
+ |
=1. |
|||
|
a2 |
b2 |
||||
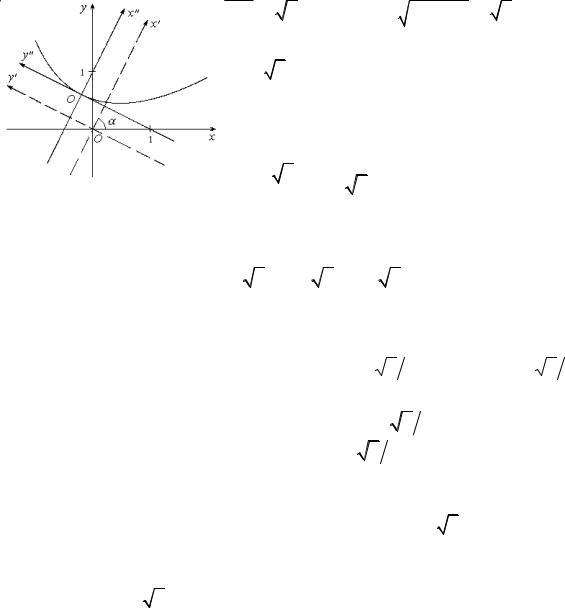
Задача 18. Привести к каноническому виду уравнение
4x2 – 4xy + y2 – 2x – 14y + 7 = 0.
Решение
Система уравнений для нахождения центра кривой (формула (6) п.4.4)
|
4x |
− 2y |
−1 = 0, |
несовместна, |
||
|
0 |
0 |
||||
|
−2x0 + y0 −7 = 0 |
значит, данная кривая центра не имеет. Не меняя начала координат, повернем оси на некоторый угол α, соответствующие преобразования координат имеют
x = x′cosα − y′sin α,
вид:
y = x′sin α+ y′cosα.
44
Перейдем в левой части уравнения к новым координатам: 4x2 – 4xy + y2 – 2x – 14y + 7 = (4cos2α — 4cosα sinα + sin2α) x′2 +
+2 (-4sinα cosα — 2cos2α + 2sin2α + sinα cosα) x′y′+
+(4sin2α + 4sinα cosα + cos2α) y′2 +
+2 (-cosα — 7sinα) x′+ 2 (sinα — 7cosα) y′+ 7. (*)
Постараемся теперь подобрать угол α так, чтобы коэффициент при х′у′ обратился в нуль. Для этого нам придется решить тригонометрическое уравнение -4sinα cosα — 2cos2α + 2sin2α + sinα cosα = 0.
Имеем 2sin2α — 3sinα cosα — 2cos2α = 0, или 2tg2α — 3tgα — 2 = 0.
Отсюда tgα = 2, или tgα = -1/2. Возьмем первое решение, что соответствует повороту осей на острый угол. Зная tgα, вычислим cosα и sinα:
|
cosα = |
1 |
= |
1 |
, |
sin α = |
tgα |
= |
2 |
. |
||
|
+tg2α |
5 |
+tg2α |
5 |
||||||||
|
1 |
1 |
Отсюда, и учитывая (*), находим уравнение данной кривой в системе х′,у′:
|
5y |
′2 |
′ |
− 2 |
5y |
′ |
+ 7 |
= 0. |
(**) |
|
−6 5x |
Дальнейшее упрощение уравнения (**) производится при помощи параллельного перенесения осей Ох′, Оу′.
Перепишем уравнение (**) следующим образом:
|
5( y |
′2 |
− 2 |
5 |
′ |
′ |
+ 7 = 0. |
|
|
5 |
|||||||
|
y ) −6 5x |
Дополнив выражение в первой скобке до полного квадрата разности и компенсируя это дополнение надлежащим слагаемым, получим:
|
′ |
5 |
2 |
6 5 |
′ |
5 |
||||||
|
y |
− |
− |
− |
= 0. |
|||||||
|
5 |
5 |
x |
5 |
||||||||
|
Введем теперь еще новые координаты х′′,у′′, полагая |
|||||||||
|
x′= x′′+ 5 5, |
y′= y′′+ 5 5, |
||||||||
|
что соответствует |
параллельному перемещению |
||||||||
|
осей на величину |
5 5 в направлении оси Ох′ и |
||||||||
|
на величину 5 5 |
в |
направлении оси Оу′. В |
|||||||
|
координатах х′′у′′ уравнение данной линии |
|||||||||
|
принимает вид |
|||||||||
|
y |
′′ |
= |
6 5 |
′′2 |
. |
||||
|
5 |
|||||||||
|
x |
|||||||||
|
Это есть каноническое уравнение параболы с |
|||||||||
|
параметром p = |
3 5 |
и с вершиной в начале координат системы х′′у′′. Парабола |
|||||||
|
5 |
|||||||||
расположена симметрично относительно оси х′′ и бесконечно простирается в
45
положительном направлении этой оси. Координаты вершины в системе х′у′
|
5 |
5 |
1 |
3 |
||||||||
|
; |
а в системе ху |
− |
; |
. |
|||||||
|
5 |
5 |
5 |
5 |
||||||||
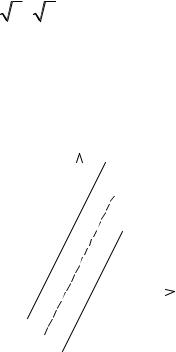
Задача 19. Какую линию определяет уравнение 4x2 — 4xy + y2 + 4x — 2y — 3 =0?
Решение
Система для нахождения центра кривой в данном случае имеет вид:
|
4x − 2y |
+ 2 = 0, |
||||
|
y |
2x-y+3=0 |
0 |
0 |
||
|
2x-y+1=0 |
−2x0 + y0 −1 = 0. |
||||
|
2x-y-1=0 |
Эта система равносильна одному уравнению 2х0 – у0 |
||||
|
+ 1 = 0, следовательно, линия имеет бесконечно |
|||||
|
много центров, составляющих прямую 2х – у + 1= 0. |
|||||
|
x |
Заметим, что левая часть данного уравнения |
||||
|
разлагается на множители первой степени: |
|||||
|
0 |
|||||
|
4х2 – 4ху + у2 + 4х –2у –3 = |
|||||
|
= (2х – у +3)(2х – у – 1). |
|||||
Значит, рассматриваемая линия есть пара параллельных прямых: 2ху – у +3 = 0 и 2х – у – 1 = 0.
|
Задача 20 |
|||||
|
1. Уравнение 5х2 + 6ху + 5у2 – 4х + 4у + 12 = 0 |
′2 |
y |
′2 |
||
|
приводится к каноническому виду х′2 + 4у′2 + 4 = 0, или |
x |
+ |
= −1. |
||
|
4 |
|||||
|
1 |
Это уравнение похоже на каноническое уравнение эллипса. Однако оно не определяет на плоскости никакого действительного образа, так как для любых действительных чисел х′,у′ левая часть его не отрицательна, а cправа стоит –1. Такое уравнение и аналогичные ему называются уравнениями мнимого эллипса.
|
2. Уравнение 5х2 + 6ху + 5у2 – 4х + 4у + 4 = 0 |
′2 |
y |
′2 |
||
|
приводится к каноническому виду х′2 + 4у′2 = 0, или |
x |
+ |
= 0. |
||
|
4 |
|||||
|
1 |
Уравнение также похоже на каноническое уравнение эллипса, но определяет не эллипс, а единственную точку: х′ = 0, у′ = 0. Такое уравнение и аналогичные ему называются уравнениями вырожденного эллипса.
Задача 21. Составить уравнение параболы, если ее фокус находится в точке F(2, -1) и уравнение директрисы D: x – y – 1 = 0.
Решение
Пусть в некоторой системе координат х′О1у′ парабола имеет канонический вид у′2 = 2рх′. Если прямая у = х – 1 является ее директрисой, то оси системы координат х′О1у′ параллельны директрисе.
46

Координаты вершины параболы, совпадающей с новым началом координат О1, найдем как середину отрезка нормали к директрисе D, проходящей через фокус.
Итак, ось О1х′описывается уравнением
у = -х + b, —1 = —2 + b. Откуда b = 1 и О1х′: у = -х + 1.
Координаты точки K пересечения директрисы и оси О1х′ находим из условия:
|
y = |
x −1 |
, |
→ xК =1, yK = 0. |
|
y = −x +1 |
|
Координаты |
нового начала координат О1(х0, у0): |
|||||
|
x =1+ 2 |
= 3 |
; y = −1+ 0 |
= −1 . Оси новой системы |
координат повернуты |
||
|
0 |
2 |
2 |
0 |
2 |
2 |
|
|
2. |
||||||
|
относительно старой на угол (-45°). Найдем р = KF = |
Итак, уравнение параболы в старой системе координат получим, если
|
подвергнем уравнение параболы y′2 = 2 |
x′ преобразованию (см. формулу (5) |
||||||||||||||||||
|
2 |
|||||||||||||||||||
|
п.4.3): |
|||||||||||||||||||
|
3 |
1 |
2 |
|||||||||||||||||
|
x′ = |
x − |
2 |
cos(−45°) + y + |
2 |
sin(−45°), |
x′ |
= |
(x − y − 2), |
|||||||||||
|
2 |
|||||||||||||||||||
|
→ |
|||||||||||||||||||
|
3 |
1 |
2 |
|||||||||||||||||
|
y′ = − x − |
sin(−45°) + y + |
cos(−45°) |
y′ |
= |
(x + y −1), |
||||||||||||||
|
2 |
2 |
2 |
|||||||||||||||||
|
y |
′2 |
′ |
1 |
(x + y |
−1) |
2 |
= 2 2 |
2 |
(x − y − 2), |
||||||||||
|
2 |
2 |
||||||||||||||||||
|
= 2 2 x |
откуда искомое уравнение параболы имеет вид: х2 + 2ху + у2 – 6х + 2у + 9 = 0. Задача 22. Написать уравнение гиперболы, если известны ее эксцентриситет
|
е = 5, фокус F(2, -3) и уравнение директрисы |
y′ |
y |
|||||
|
3х – у + 3 = 0. |
D1 |
||||||
|
Решение |
3 B |
||||||
|
Уравнение директрисы D1: у = 3х + 3 позволяет |
|||||||
|
заключить, что новая ось координат Ох′ имеет |
|||||||
|
вид y = (-1/3)x + b, проходит через точку F(2, — |
-7 |
-1 |
α |
x |
|||
|
1 |
+b, |
откуда b = -7/3 и Ох′ |
O1 |
A |
0 |
||
|
3), значит, −3 = −3 2 |
K |
||||||
|
1 x − |
7 . |
a / |
5 |
-7/3 |
x′ |
||
|
задается уравнением |
y = − |
F |
|||||
|
3 |
3 |
Пусть начало новой системы координат находится в точке О1(х0, у0). Найдем координаты точки К как координаты точки пересечения директрисы D1 и
47
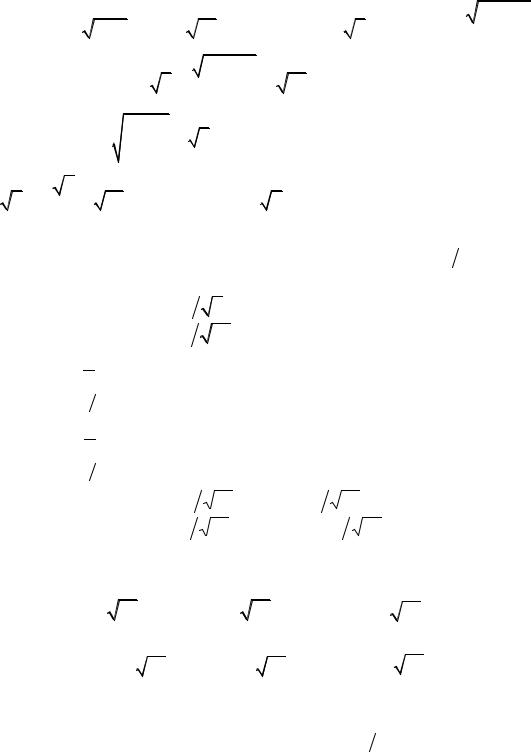
|
3x − y +3 = 0, |
→ xK |
= − |
8 |
, yK |
= − |
9 . |
|
оси Ох′′ из системы |
3y + x + 7 |
= 0 |
||||
|
5 |
5 |
|
Геометрические свойства |
гиперболы, |
которая |
в |
новых |
осях |
координат |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ох′у′имеет вид |
x |
′2 |
y |
′2 |
=1, |
позволяют найти КF как расстояние от фокуса |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
− |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a2 |
b2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
F(2, -3) до директрисы D1: 3х – у + 3 = 0. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
KF = |
3 (2) −(−3) +3 |
= |
12 |
, |
O K |
= a = |
a |
, |
O F |
= c = |
a2 +b2 , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9 +1 |
10 |
1 |
e |
5 |
1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
O K =O F |
− KF |
a |
= a2 +b2 − |
12 |
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
1 |
5 |
10 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
так |
как |
e = |
1+ |
b2 |
= |
5, |
b |
2 |
= 4a |
2 |
. Значение |
а |
находим |
из |
уравнения |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
12 |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= a |
5 − |
и получаем a = |
. При этом b2 = 18. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
10 |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
′2 |
y |
′2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Уравнение гиперболы в новых координатах имеет вид |
x |
− |
=1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9 2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
18 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Координаты нового центра найдем, зная что точка К делит отрезок О1F в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
отношении λ = |
O1K |
= |
a |
5 |
= |
1 |
: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
10 |
4 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
KF |
12 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x0 |
+ |
1 |
xF |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
5 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
xK |
= |
, |
x0 = − |
, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
+ |
1 4 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
откуда |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
y0 + |
yF |
y0 = − |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
2 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
yK |
= |
, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
+1 4 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Из ∆ АВО: sinα = 1 |
10 , |
cosα = 3 |
10 . Так как поворот совершается на |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
угол (-α): sin(-α) = −1 |
10 , cos(-α) = 3 |
10 , |
то формулы преобразований |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
координат (см. (5) в п.4.3) принимают вид: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 3 |
3 |
1 |
1 |
(3x − y + 6), |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x′ = x |
+ |
2 |
+ |
y |
+ |
2 |
− |
, |
x′ |
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
10 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
10 |
10 |
→ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
1 |
3 |
3 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(x +3y + 7) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
y′ |
= − |
x + |
− |
+ |
y |
+ |
2 |
, |
y′ = |
10 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
10 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
10 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
(3x − y + 6)2 |
1 |
(x +3y + 7)2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
10 |
10 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
и уравнение гиперболы принимает вид |
− |
=1, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9 2 |
18 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4(3х – у +6)2 – (х + 3у + 7)2 = 180 |
или 7х2 – у2 – 6ху – 18у + 26х + 17 = 0. |
48
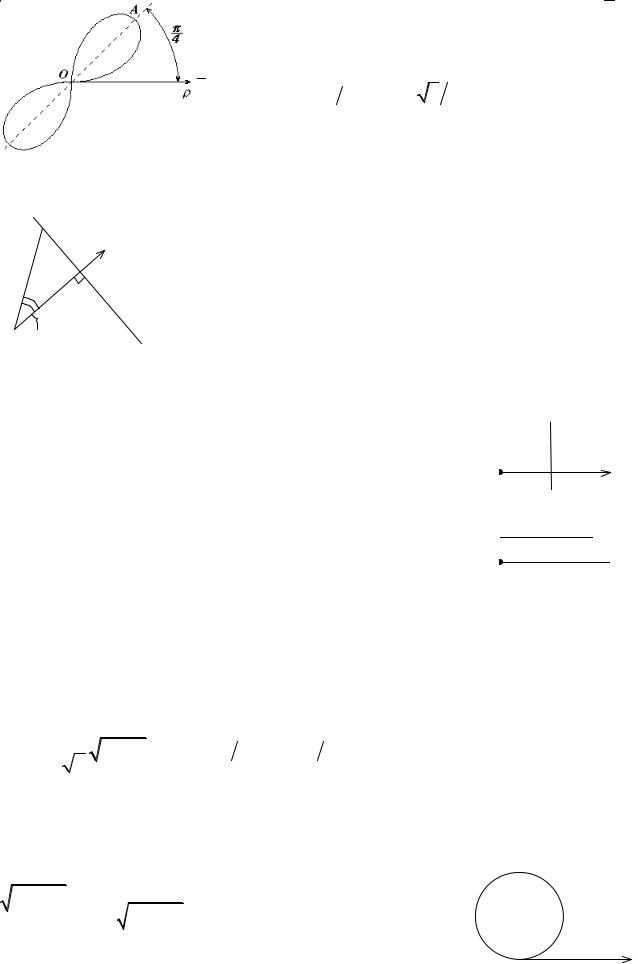
Задача 23. Найти полярный угол отрезка, направленного из точки (5, 
точку (6, 2
Решение
|
ρ= (6 −5)2 + (2 3 − 3)2 = 2, |
cosϕ =1 2, sin ϕ = 3 2 ϕ= 60°. |
(см. п.5.2).
Задача 24. Составить уравнение прямой в полярных координатах, считая известными расстояние р от полюса до прямой и угол α от полярной оси до луча, направленного из полюса перпендикулярно к прямой.
Решение
Известны ОР = р, РОА = α, произвольная точка М прямой L имеет координаты (ρ, ϕ).
Точка М лежит на прямой L в том и только в том случае,
αкогда проекция точки М на луч ОР совпадает с точкой Р,
|
т.е. когда р = ρ cosβ, где РОМ = β. Угол ϕ = α + β и |
|||
|
O |
A |
||
|
уравнение прямой L принимает вид ρ cos(ϕ — α) = p. |
Задача 25. Найти полярные уравнения указанных кривых: 1). x = a, a > 0
Решение
ρ cosϕ = a → ρ = a/cosϕ.
2). y = b, b > 0
Решение
|
ρ sinϕ = b |
→ ρ = b/sinϕ. |
0 |
||||||
|
3). (х2 + у2)2 = а2ху |
||||||||
|
Решение: xy ≥ 0, |
||||||||
|
ρ4 = a2ρ2 cosϕsin ϕ→ ρ2 = a2 |
sin 2ϕ, |
sin 2ϕ≥ 0. |
||||||
|
2 |
||||||||
|
Уравнение кривой в полярных координатах имеет |
||||||||
|
вид ρ = |
a |
sin 2ϕ, ϕ [0, π 2] [π, 3π 2] и задает |
||||||
|
2 |
двухлепестковую розу:
Задача 26. Построить заданные в полярной системе координат линии: 1). ρ = 2a sinϕ, a > 0.
|
Решение |
y |
|||||
|
x2 + y2 = 2a |
, |
|||||
|
x2 |
+ y2 |
|||||
|
a |
||||||
|
x2 + y2 – 2ay = 0, |
0 |
|||||
b
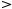
ρ
49
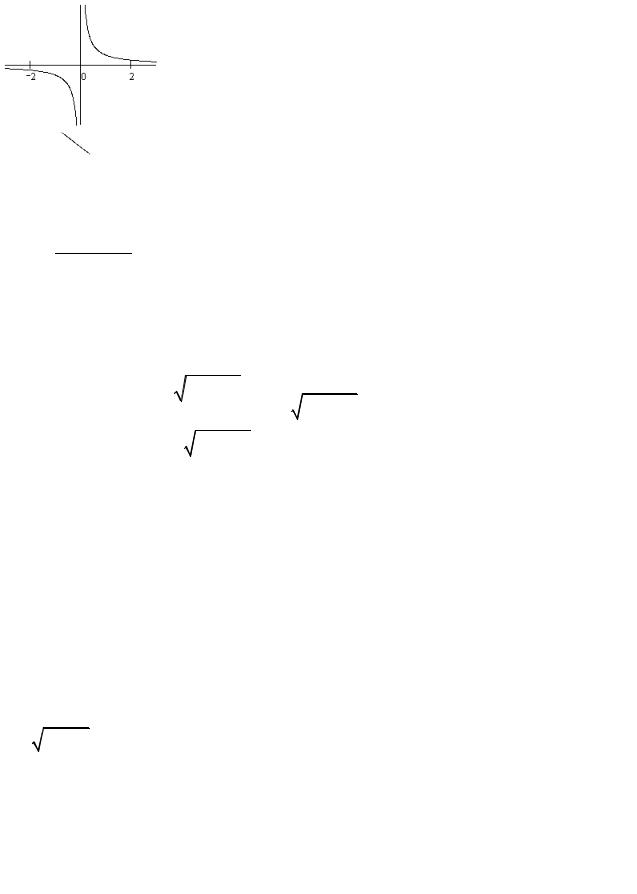
x2 + (y – a)2 = a2. 2). ρ = 2 + cosϕ.
Решение
Линия получается, если каждый радиус-вектор окружности
ρ = cosϕ увеличить на два. Найдем координаты контрольных точек:
ϕ= 0, ρ = 3;
ϕ= π/2, ρ = 2;
ϕ= π, ρ = 1.
3). ρ = 9
4 −5cosϕ
Решение
4 – 5 cosϕ > 0, cosϕ < 4/5, ϕ (arccos(4/5), 2π – arccos(4/5)).
При этом ρ (4 — 5 cosϕ) = 9. Переходя к декартовым координатам, получаем
|
x |
2 |
+ y |
2 |
x |
|||||||
|
4 |
−5 |
= 9, |
|||||||||
|
x |
2 |
+ y |
2 |
||||||||
4 x2 + y2 = 5x +9, 16(x2 + y2 )= (5x +9)2 ,
16x2 + 16y2 = 25x2 + 90x + 81, 9x2 + 90x – 16y2 +81 = 0,
|
2 |
2 |
(x +5)2 |
y |
2 |
|||||
|
9(x + 5) |
– 16y = 144 |
→ |
2 |
− |
=1 |
||||
|
4 |
3 |
2 |
|||||||
гиперболы при указанных ϕ.
Кривую можно было построить по точкам, например, при ϕ = π 4). ρ2 sin2ϕ = а2.
Решение
sin 2ϕ≥ 0, ϕ [0, π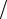
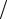
|
ρ = |
a |
. |
|||
|
sin 2ϕ |
|||||
Перейдем к декартовым координатам, учтем, что
|
sin 2ϕ = 2cos ϕ sin ϕ |
ρ2 |
= |
2xy |
, |
|
|
ρ2 |
x2 + y2 |
||||
тогда кривая принимает вид гиперболы: y = a2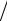
Задача 27. Какие линии задаются следующими параметрическими уравнениями:
50

|
x = 3cost, |
t [0, 2π]. |
|||||||
|
1). |
||||||||
|
y = 2sin t, |
||||||||
|
Решение |
||||||||
|
x2 |
y2 |
|||||||
|
+ |
=1 — эллипс. |
|||||||
|
2 |
2 |
2 |
||||||
|
3 |
||||||||
|
2 |
||||||||
|
2). x = t |
− 2t |
+1, t R. |
||||||
|
y = t −1, |
Решение
у2 = x – парабола.
|
x = −1 + 2 cost, |
t [0, 2π]. |
|
3). |
y = 3 + 2sin t, |
Решение
(x + 1)2 + (y – 3)2 = 4 –окружность;
|
x = 2t −1, |
t R. |
|
|
4). |
− 4t2 |
, |
|
y =1 |
Решение
y = -x2 – 2x, y – 1 = -(x + 1)2 – парабола с вершиной в точке (-1, 1).
|
3 |
||||
|
Задача 28. Выведите уравнение астроиды x = acos |
t, |
t [0, 2π], |
||
|
y = asin3 t, |
в полярной системе координат.
Решение
x2 + y2 = a2(sin6t + cos6t) = a2(sin2t + cos2t) (sin4t + cos4t – sin2t cos2t) =
=a2(sin4t + cos4t + 2sin2t cos2t – 3sin2t cos2t) = a2((sin2t + cos2t)2 – 3sin2t cos2t) =
=a2(1 – 3sin2t cos2t) = a2(1 – (3/4) sin22t).
51
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
11.05.2015358.91 Кб31UK.doc
- #
- #
- #
- #
- #
- #
- #