Определение
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Замечание
Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию. Параллельность” и “Перпендикулярность. Углы и расстояния в пространстве”.
Важные определения
1. Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.
2. Две прямые в пространстве скрещиваются, если через них нельзя провести плоскость.
3. Прямая и плоскость параллельны, если они не имеют общих точек.
4. Две плоскости параллельны, если они не имеют общих точек.
5. Две прямые в пространстве называются перпендикулярными, если угол между ними равен (90^circ).
6. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
7. Две плоскости называются перпендикулярными, если угол между ними равен (90^circ).
Важные аксиомы
1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Важные теоремы
1. Если прямая (a), не лежащая в плоскости (pi), параллельна некоторой прямой (p), лежащей в плоскости (pi), то она параллельна данной плоскости.
2. Пусть прямая (p) параллельна плоскости (mu). Если плоскость (pi) проходит через прямую (p) и пересекает плоскость (mu), то линия пересечения плоскостей (pi) и (mu) — прямая (m) — параллельна прямой (p).
3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.
4. Если две параллельные плоскости (alpha) и (beta) пересечены третьей плоскостью (gamma), то линии пересечения плоскостей также параллельны:
[alphaparallel beta, alphacap gamma=a, betacapgamma=b Longrightarrow aparallel b]
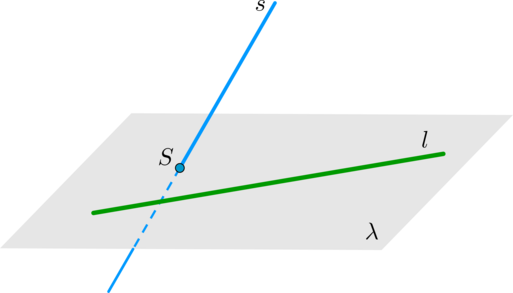
5. Пусть прямая (l) лежит в плоскости (lambda). Если прямая (s) пересекает плоскость (lambda) в точке (S), не лежащей на прямой (l), то прямые (l) и (s) скрещиваются.
6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.
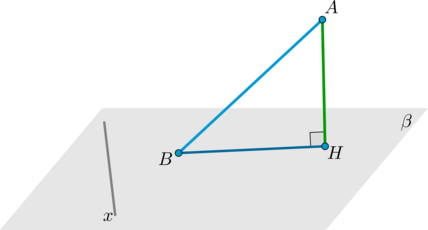
7. Теорема о трех перпендикулярах.
Пусть (AH) – перпендикуляр к плоскости (beta). Пусть (AB, BH) – наклонная и ее проекция на плоскость (beta). Тогда прямая (x) в плоскости (beta) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.
8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.
Замечание
Еще один важный факт, часто использующийся для построения сечений:
для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.
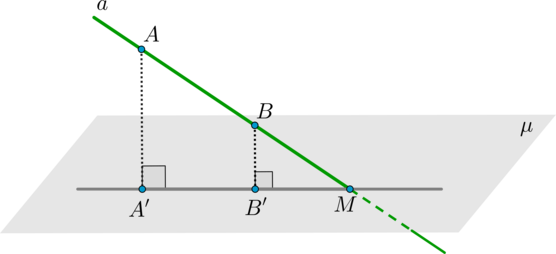
Для этого из двух произвольных точек (A) и (B) прямой (a) проведем перпендикуляры на плоскость (mu) – (AA’) и (BB’) (точки (A’, B’) называются проекциями точек (A,B) на плоскость). Тогда прямая (A’B’) – проекция прямой (a) на плоскость (mu). Точка (M=acap
A’B’) и есть точка пересечения прямой (a) и плоскости (mu).
Причем заметим, что все точки (A, B, A’, B’, M) лежат в одной плоскости.
Пример 1.
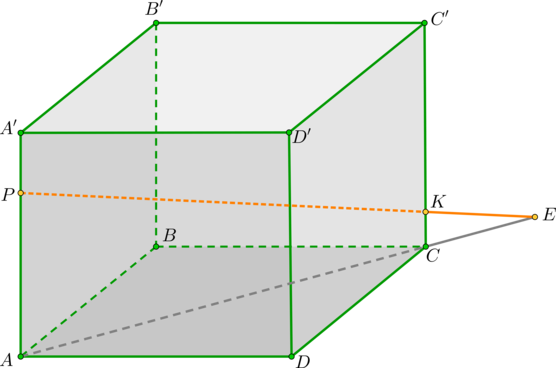
Дан куб (ABCDA’B’C’D’). (A’P=dfrac 14AA’, KC=dfrac15 CC’). Найдите точку пересечения прямой (PK) и плоскости (ABC).
Решение
1) Т.к. ребра куба (AA’, CC’) перпендикулярны ((ABC)), то точки (A) и (C) — проекции точек (P) и (K). Тогда прямая (AC) – проекция прямой (PK) на плоскость (ABC). Продлим отрезки (PK) и (AC) за точки (K) и (C) соответственно и получим точку пересечения прямых – точку (E).
2) Найдем отношение (AC:EC). (triangle PAEsim triangle KCE) по двум углам ((angle A=angle C=90^circ, angle E) – общий), значит, [dfrac{PA}{KC}=dfrac{EA}{EC}]
Если обозначить ребро куба за (a), то (PA=dfrac34a, KC=dfrac15a,
AC=asqrt2). Тогда:
[dfrac{frac34a}{frac15a}=dfrac{asqrt2+EC}{EC} Rightarrow
EC=dfrac{4sqrt2}{11}a Rightarrow AC:EC=4:11]
Пример 2.
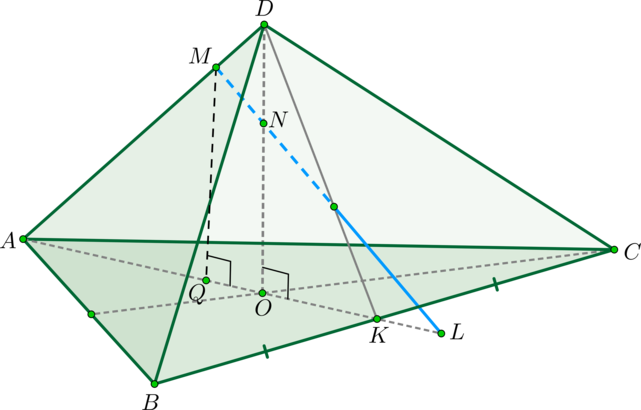
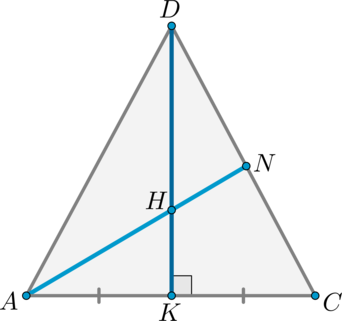
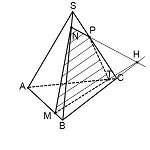
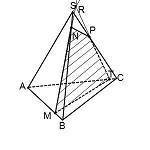
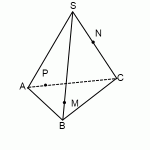
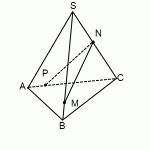
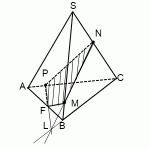
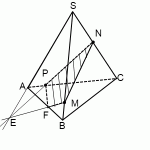
Дана правильная треугольная пирамида (DABC) с основанием (ABC), высота которой равна стороне основания. Пусть точка (M) делит боковое ребро пирамиды в отношении (1:4), считая от вершины пирамиды, а (N) – высоту пирамиды в отношении (1:2), считая от вершины пирамиды. Найдите точку пересечения прямой (MN) с плоскостью (ABC).
Решение
1) Пусть (DM:MA=1:4, DN:NO=1:2) (см. рисунок). Т.к. пирамида правильная, то высота падает в точку (O) пересечения медиан основания. Найдем проекцию прямой (MN) на плоскость (ABC). Т.к. (DOperp (ABC)), то и (NOperp (ABC)). Значит, (O) – точка, принадлежащая этой проекции. Найдем вторую точку. Опустим перпендикуляр (MQ) из точки (M) на плоскость (ABC). Точка (Q) будет лежать на медиане (AK).
Действительно, т.к. (MQ) и (NO) перпендикулярны ((ABC)), то они параллельны (значит, лежат в одной плоскости). Следовательно, т.к. точки (M, N, O) лежат в одной плоскости (ADK), то и точка (Q) будет лежать в этой плоскости. Но еще (по построению) точка (Q) должна лежать в плоскости (ABC), следовательно, она лежит на линии пересечения этих плоскостей, а это – (AK).
Значит, прямая (AK) и есть проекция прямой (MN) на плоскость (ABC). (L) – точка пересечения этих прямых.
2) Заметим, что для того, чтобы правильно нарисовать чертеж, необходимо найти точное положение точки (L) (например, на нашем чертеже точка (L) лежит вне отрезка (OK), хотя она могла бы лежать и внутри него; а как правильно?).
Т.к. по условию сторона основания равна высоте пирамиды, то обозначим (AB=DO=a). Тогда медиана (AK=dfrac{sqrt3}2a). Значит, (OK=dfrac13AK=dfrac 1{2sqrt3}a). Найдем длину отрезка (OL) (тогда мы сможем понять, внутри или вне отрезка (OK) находится точка (L): если (OL>OK) – то вне, иначе – внутри).
а) (triangle AMQsim triangle ADO) по двум углам ((angle Q=angle
O=90^circ, angle A) – общий). Значит,
[dfrac{MQ}{DO}=dfrac{AQ}{AO}=dfrac{MA}{DA}=dfrac 45
Rightarrow MQ=dfrac 45a, AQ=dfrac 45cdot dfrac 1{sqrt3}a]
Значит, (QK=dfrac{sqrt3}2a-dfrac 45cdot dfrac
1{sqrt3}a=dfrac7{10sqrt3}a).
б) Обозначим (KL=x).
(triangle LMQsim triangle LNO) по двум углам ((angle Q=angle O=90^circ, angle L) – общий). Значит,
[dfrac{MQ}{NO}=dfrac{QL}{OL} Rightarrow dfrac{frac45 a}{frac 23a}
=dfrac{frac{7}{10sqrt3}a+x}{frac1{2sqrt3}a+x} Rightarrow
x=dfrac a{2sqrt3} Rightarrow OL=dfrac a{sqrt3}]
Следовательно, (OL>OK), значит, точка (L) действительно лежит вне отрезка (AK).
Замечание
Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что (x) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки (L) (то есть, что она находится внутри отрезка (AK)).
Пример 3
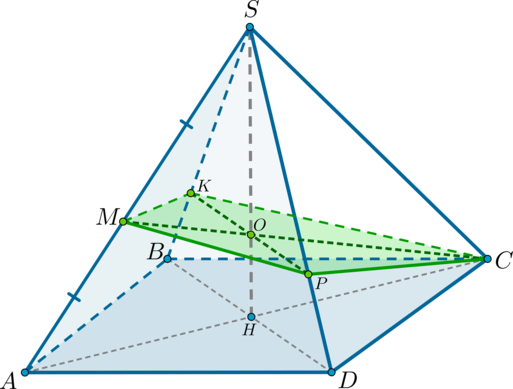
Дана правильная четырехугольная пирамида (SABCD). Найдите сечение пирамиды плоскостью (alpha), проходящей через точку (C) и середину ребра (SA) и параллельной прямой (BD).
Решение
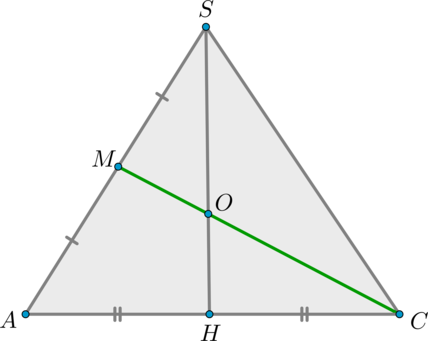
1) Обозначим середину ребра (SA) за (M). Т.к. пирамида правильная, то высота (SH) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость (SAC). Отрезки (CM) и (SH) лежат в этой плоскости, пусть они пересекаются в точке (O).
Для того, чтобы плоскость (alpha) была параллельна прямой (BD), она должна содержать некоторую прямую, параллельную (BD). Точка (O) находится вместе с прямой (BD) в одной плоскости – в плоскости (BSD). Проведем в этой плоскости через точку (O) прямую (KPparallel
BD) ((Kin SB, Pin SD)). Тогда, соединив точки (C, P, M, K), получим сечение пирамиды плоскостью (alpha).
2) Найдем отношение, в котором делят точки (K) и (P) ребра (SB) и (SD). Таким образом мы полностью определим построенное сечение.
Заметим, что так как (KPparallel BD), то по теореме Фалеса (dfrac{SB}{SK}=dfrac{SD}{SP}). Но (SB=SD), значит и (SK=SP). Таким образом, можно найти только (SP:PD).
Рассмотрим (triangle ASC). (CM, SH) – медианы в этом треугольнике, следовательно, точкой пересечения делятся в отношении (2:1), считая от вершины, то есть (SO:OH=2:1).
Теперь по теореме Фалеса из (triangle BSD): (dfrac{SP}{PD}=dfrac{SO}{OH}=dfrac21).
3) Заметим, что по теореме о трех перпендикулярах (COperp BD) как наклонная ((OH) – перпендикуляр на плоскость (ABC), (CHperp BD) – проекция). Значит, (COperp KP). Таким образом, сечением является четырехугольник (CPMK), диагонали которого взаимно перпендикулярны.
Пример 4
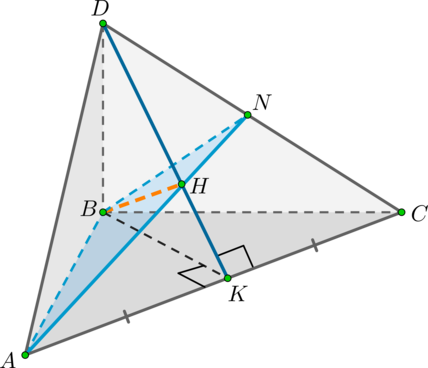
Дана прямоугольная пирамида (DABC) с ребром (DB), перпендикулярным плоскости (ABC). В основании лежит прямоугольный треугольник с (angle B=90^circ), причем (AB=DB=CB). Проведите через прямую (AB) плоскость, перпендикулярную грани (DAC), и найдите сечение пирамиды этой плоскостью.
Решение
1) Плоскость (alpha) будет перпендикулярна грани (DAC), если она будет содержать прямую, перпендикулярную (DAC). Проведем из точки (B) перпендикуляр на плоскость (DAC) — (BH), (Hin DAC).
Проведем вспомогательные (BK) – медиану в (triangle ABC) и (DK) – медиану в (triangle DAC).
Т.к. (AB=BC), то (triangle ABC) – равнобедренный, значит, (BK) – высота, то есть (BKperp AC).
Т.к. (AB=DB=CB) и (angle ABD=angle CBD=90^circ), то (triangle
ABD=triangle CBD), следовательно, (AD=CD), следовательно, (triangle DAC) – тоже равнобедренный и (DKperp AC).
Применим теорему о трех перпендикулярах: (BH) – перпендикуляр на (DAC); наклонная (BKperp AC), значит и проекция (HKperp AC). Но мы уже определили, что (DKperp AC). Таким образом, точка (H) лежит на отрезке (DK).
Соединив точки (A) и (H), получим отрезок (AN), по которому плоскость (alpha) пересекается с гранью (DAC). Тогда (triangle
ABN) – искомое сечение пирамиды плоскостью (alpha).
2) Определим точное положение точки (N) на ребре (DC).
Обозначим (AB=CB=DB=x). Тогда (BK), как медиана, опущенная из вершины прямого угла в (triangle ABC), равна (frac12 AC), следовательно, (BK=frac12 cdot sqrt2 x).
Рассмотрим (triangle BKD). Найдем отношение (DH:HK).
Заметим, что т.к. (BHperp (DAC)), то (BH) перпендикулярно любой прямой из этой плоскости, значит, (BH) – высота в (triangle DBK). Тогда (triangle DBHsim triangle DBK), следовательно
[dfrac{DH}{DB}=dfrac{DB}{DK} Rightarrow DH=dfrac{sqrt6}3x
Rightarrow HK=dfrac{sqrt6}6x Rightarrow DH:HK=2:1]
Рассмотрим теперь (triangle ADC). Медианы треугольника точной пересечения делятся в отношении (2:1), считая от вершины. Значит, (H) – точка пересечения медиан в (triangle ADC) (т.к. (DK) – медиана). То есть (AN) – тоже медиана, значит, (DN=NC).
На этой странице вы узнаете
- Как дракон с помощью сечений разрушал город?
- Чем вода похожа на сечение?
- Что общего у следа на снегу и следа в сечении?
Заглянем в кинотеатр имени Математики. Какой фильм сейчас будут показывать? Располагайтесь поудобнее, приятного просмотра…
Сечения
Как дракон с помощью сечений разрушал город?
…В далеком будущем, на одной из недавно открытых планет, люди построили новую цивилизацию. Они возвели новые дома для комфортной жизни разных необычных форм.
Но внезапно с другой, темной стороны планеты, появился дракон, коренной обитатель планеты. Ему не понравилось вторжение людей, и решил он стереть в пыль все строения.
Он прилетал к домам, раскрывал свою пасть и стрелял страшным красным лучом. И каждая поверхность и каждый объем, которого касался этот луч, разрезался по прямой линии.

Прилетел дракон к пирамиде и разрезал ее. Ахнули люди: верхушка пирамиды съехала, осталась лишь прямоугольная плоскость.
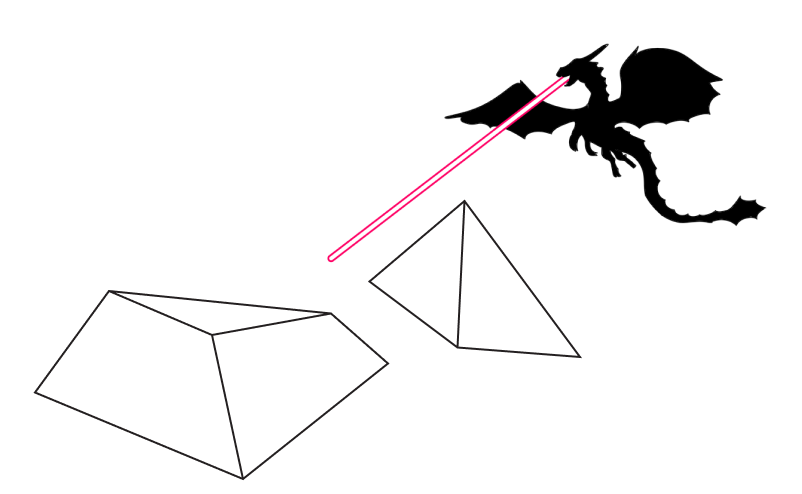
Увидел дракон обычный дом — в форме параллелепипеда, — и снова луч разрезал здание. Осталась вместо крыши дыра в форме четырехугольника.
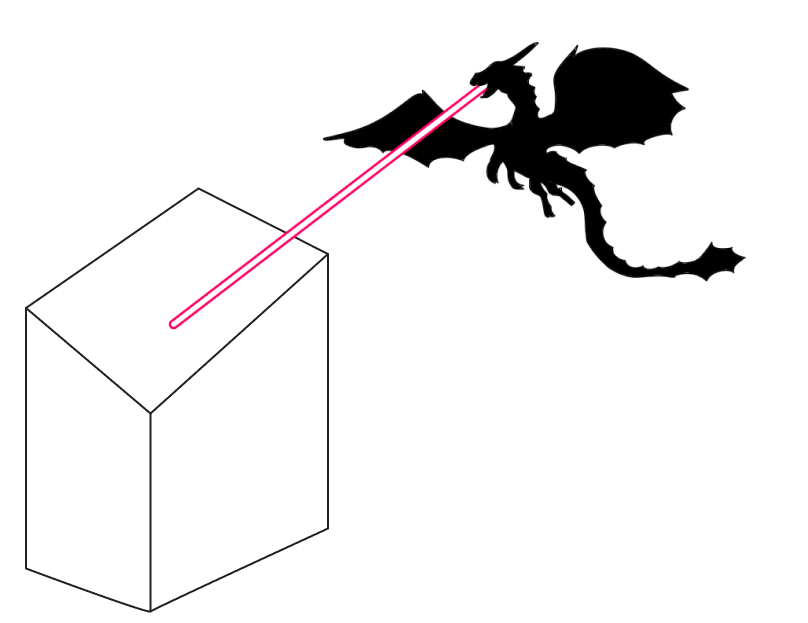
Долетел змей до памятника того народа: “треугольной” башни. Разрушил и это здание. Раскололось здание на две половинки, а в месте их раскола остались треугольные дыры.
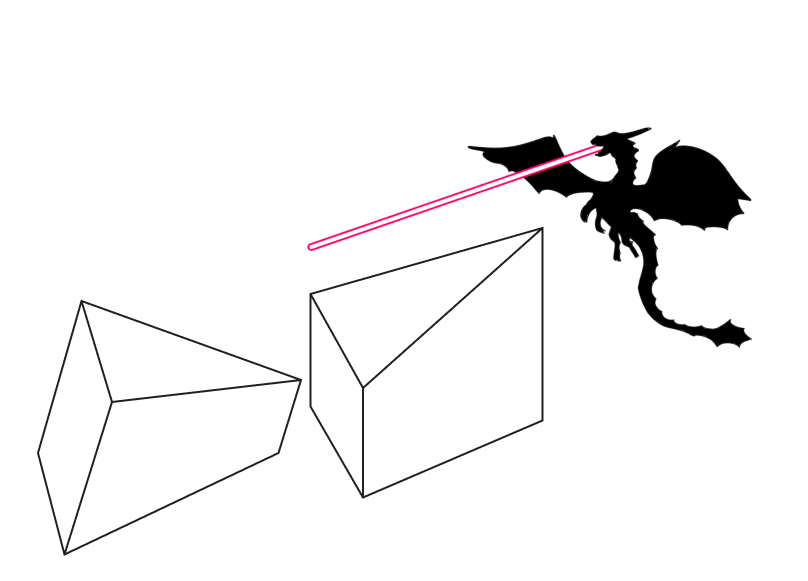
Поняли люди: нет сил это терпеть! Собрали межгалактические войска и победили дракона. А после восстанавливали город и удивлялись: как интересно были разрезаны здания.
Так что же делал дракон? Он разрезал геометрические тела, а на месте их разреза оставались сечения.
Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью.
Разумеется, никакой дракон не прилетает и не рассекает наши рисунки в тетради. Все сечения чертятся отдельно, а представляются мысленно.
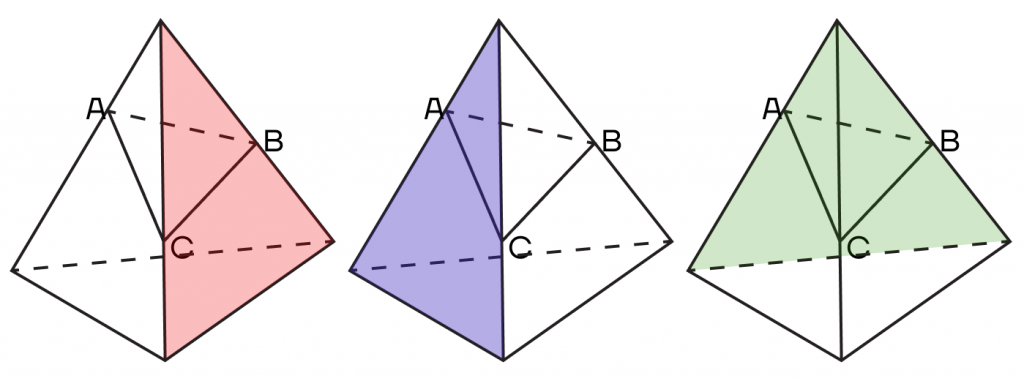
Заметим, что в многогранниках сечение получается в форме многоугольника, вершины которого лежат на ребрах многогранника, а стороны на гранях. Обратим внимание, что две соседние вершины будут принадлежать одной и той же грани, то есть одной плоскости.
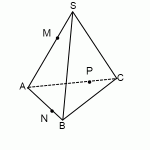
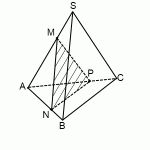
Рассмотрим сечение пирамиды АВС: вершины А, В и С лежат точно на ребрах.
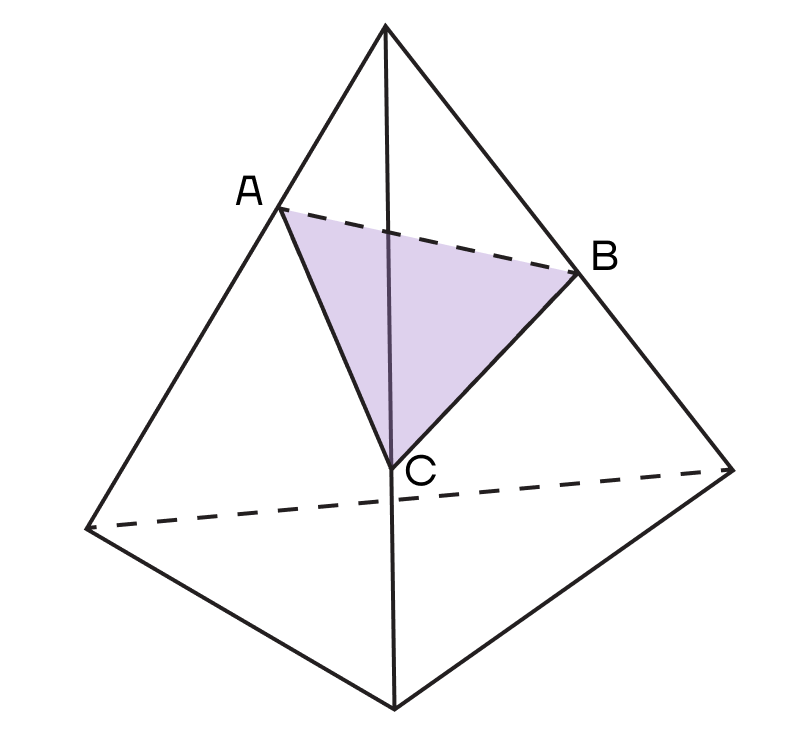
При этом пары вершин А и В, В и С, А и С лежат в одной грани и принадлежат одной плоскости.
Сечение геометрических тел является очень интересным разделом стереометрии. Поскольку это раздел стереометрии, в нем действуют все ее законы, в том числе и аксиомы стереометрии. В этой статье мы не будем заострять на них внимание, прочитать подробнее можно в статье «Аксиомы стереометрии. Расположение прямых и плоскостей в пространстве».
Зачем может потребоваться сечение?
Мы сталкиваемся с ними намного чаще, чем думаем. Они бывают не только в задачах, но и встречаются в жизни.
Что мы делаем, когда нарезаем салат? Рассекаем овощи. Каждый разрез — это сечение.

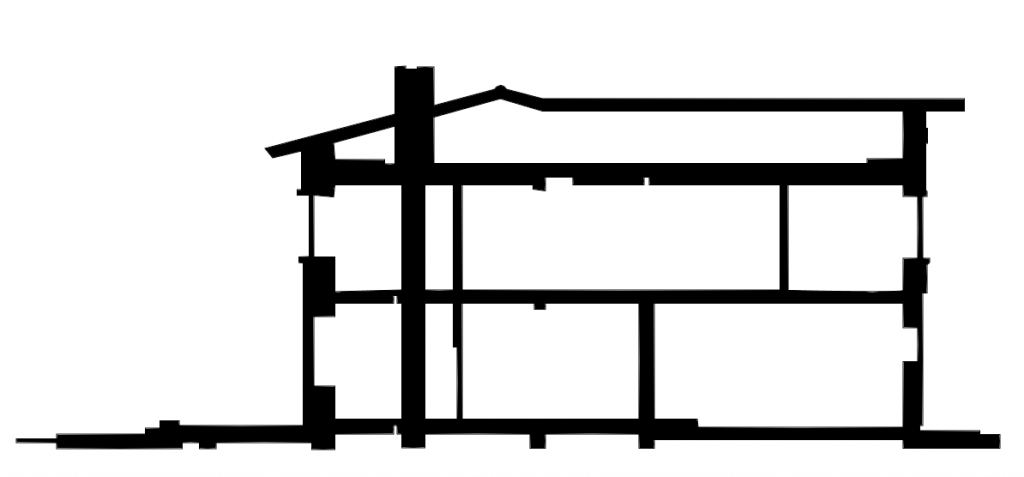
А что делают архитекторы, когда чертят разрезы? Мысленно рассекают здание и показывают его “внутренности”.
Посмотрим на бутылку с водой. Верхний уровень воды можно принять за плоскость, которая рассекает тело бутылки. Наклоняя бутылку и меняя положение воды, можно увидеть различные сечения, которые могут в ней появиться.

Сечения окружают нас, и в них совсем нет ничего сверхъестественного. А поэтому и разобраться в сечениях в стереометрии не составит для нас труда.
Методы построения сечений
Однако сечения нужно правильно построить. Для их построения существует несколько методов:
- Метод следов;
- Метод внутреннего проектирования;
- Комбинированный метод.
Разберем их по порядку.
Зимой очень интересно гулять по лесу и разглядывать следы животных: вот пробежал заяц, а это, кажется, была маленькая лисица. Здесь просто снег упал с веток дерева.

Все эти тела оставляют след на снегу.
Сечение так же, как и любое животное на снегу, оставляет след на гранях многогранника. И этот след — это сторона многоугольника, который образовывает сечение.
Если мы возьмем карандаш и проведем прямую на листе, он оставит след. Также и плоскость сечения как бы проводит карандашом по граням фигур, оставляя после себя следы.
След плоскости а в плоскости основания многогранника — прямая, по которой секущая плоскость пересекает плоскость основания многогранника.
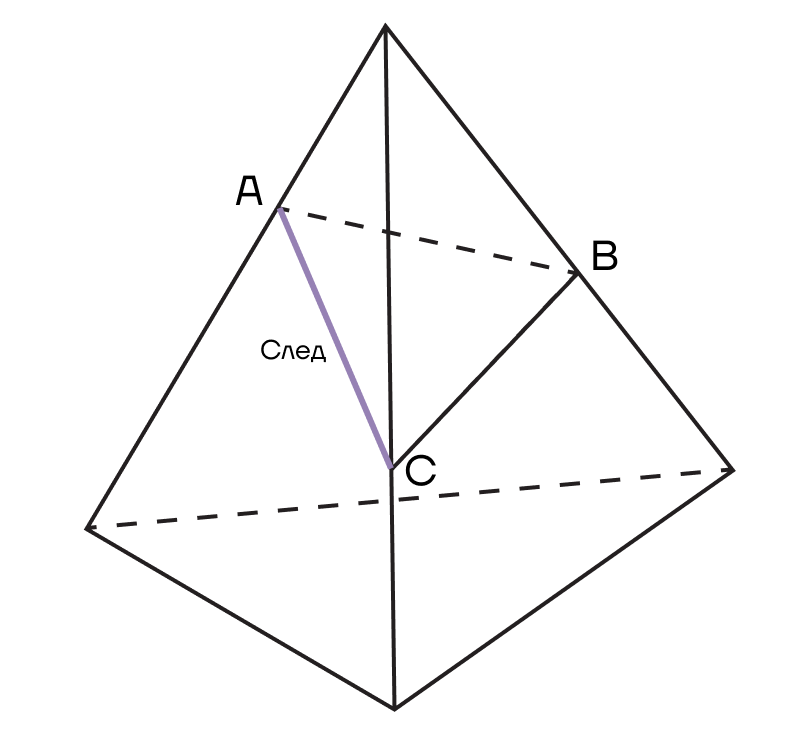
Вспомним, что плоскость бесконечна, значит, и след можно продолжать в разные стороны бесконечно.
Однако для построения сечений необходимости бесконечно его продолжать нет: достаточно до пересечения с ребром многогранника или продолжением ребра.
Построим сечение куба, которое проходит через точки К, М и Т, чтобы чуть подробнее разобраться в методе следов.
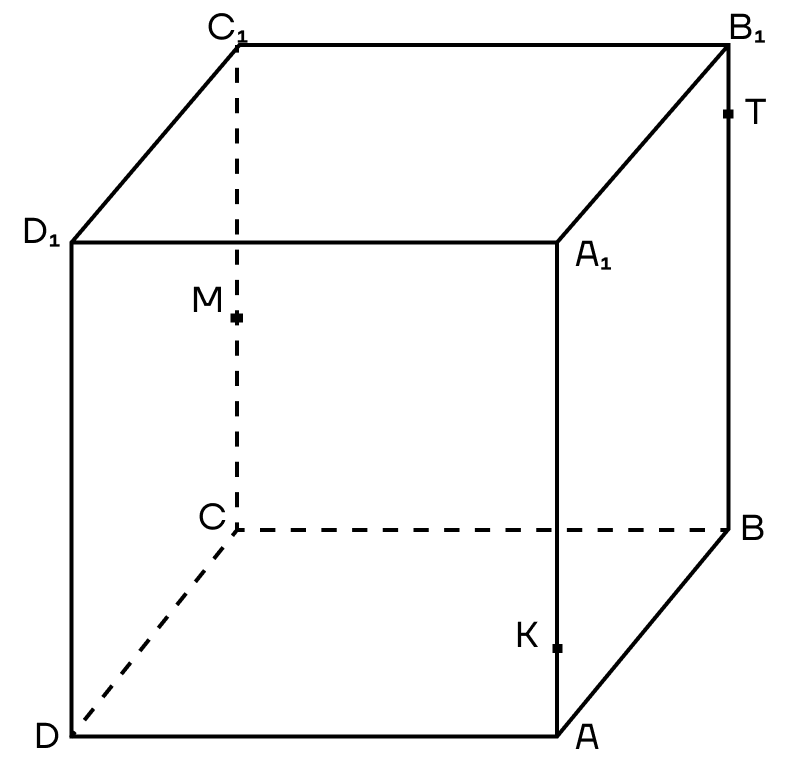
При построении сечений существует очень важный лайфхак: если точки лежат в одной плоскости (то есть в одной грани), то их можно соединить.
1. Заметим, что в нашем кубе это точки К и Т в плоскости (АВВ1) и точки М и Т в плоскости (ВСС1). Поэтому мы можем их соединить.
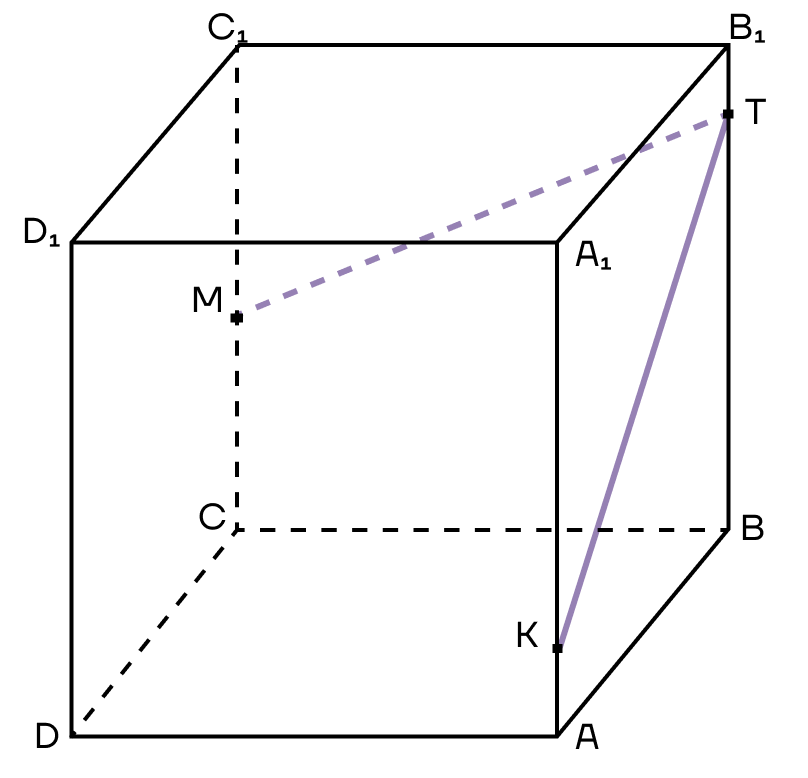
2. КТ и МТ в нашем случае — это следы плоскости сечения. Продолжим их за точку К и за точку М. Аналогично продолжим стороны АВ и ВС до тех пор, пока их продолжения не пересекутся со следами.
Пусть продолжения прямых АВ и ТК пересекутся в точке Н, а продолжения прямых ТМ и ВС пересекутся в точке F.
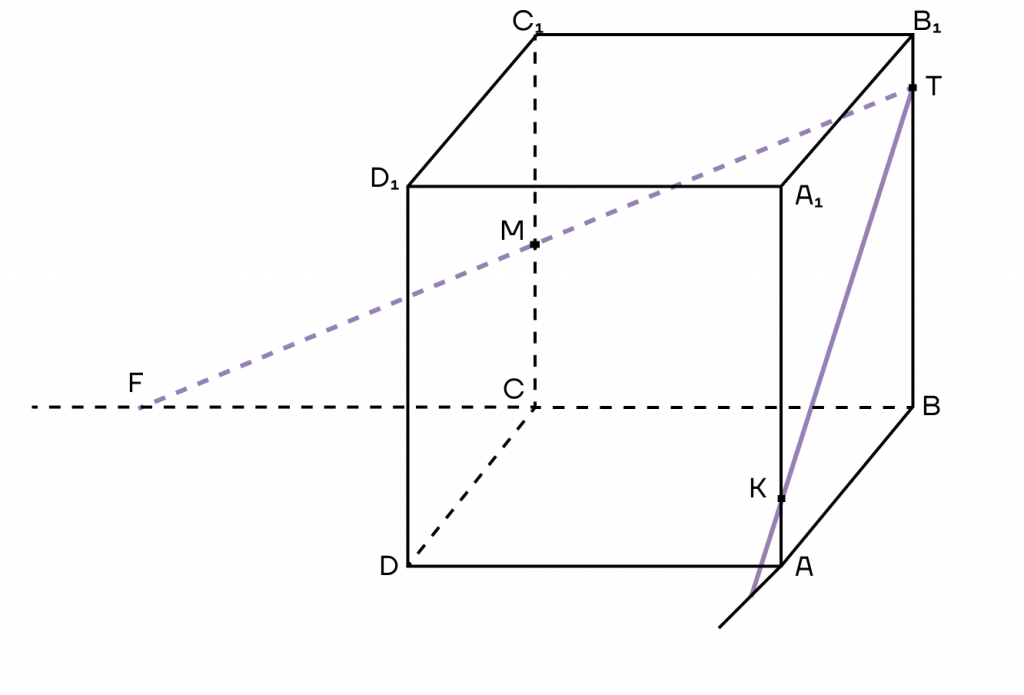
3. Обратим внимание, что точки Н и F лежат на продолжении ребер основания, а значит, лежат в плоскости основания куба. Пользуясь лайфхаком, их можно соединить. Таким образом, получим треугольник, который как бы разрезает наш куб.
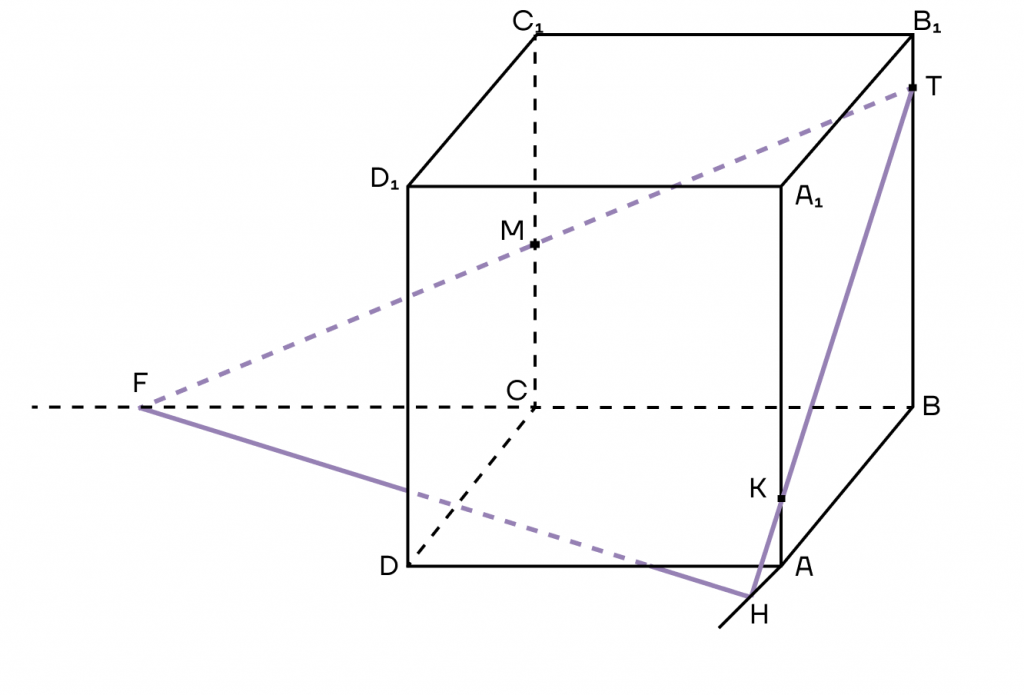
4. Однако наше сечение не закончено. Вспомним, что все вершины многоугольника должны лежать на ребрах куба, то есть точки Н и F не подходят. Но на самом деле осталось совсем немного закончить построение.
5. Заметим, что прямая HF пересекает ребра AD, DC, назовем точки этих пересечений как N и L.
А также соединим все точки, которые окажутся в одной плоскости.
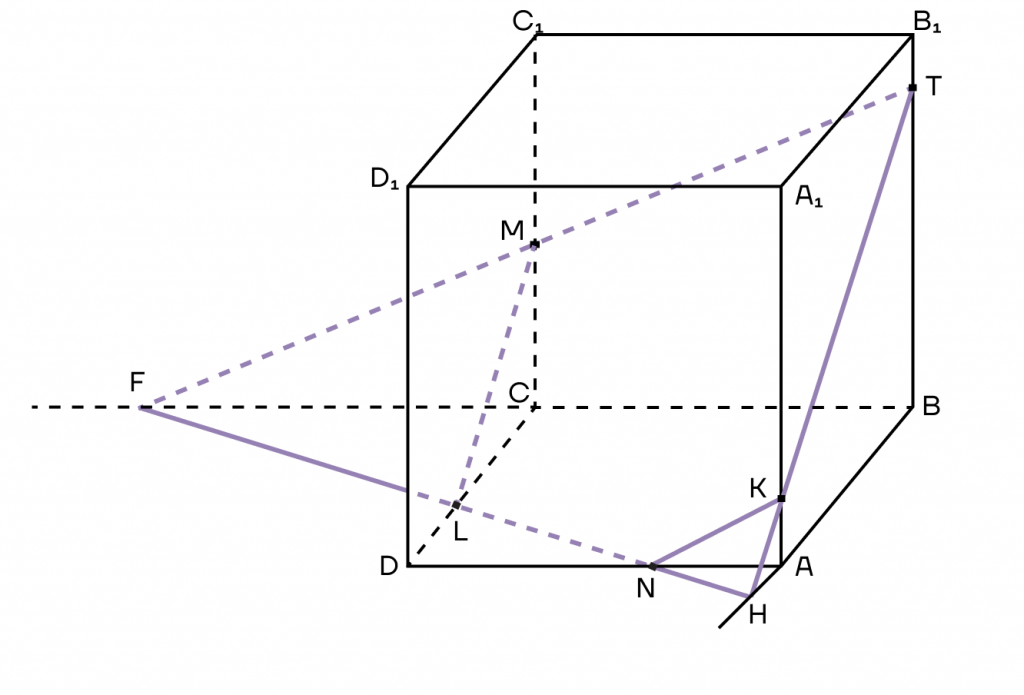
6. И вот мы получили сечение. Многоугольник TKNLM — сечение куба.
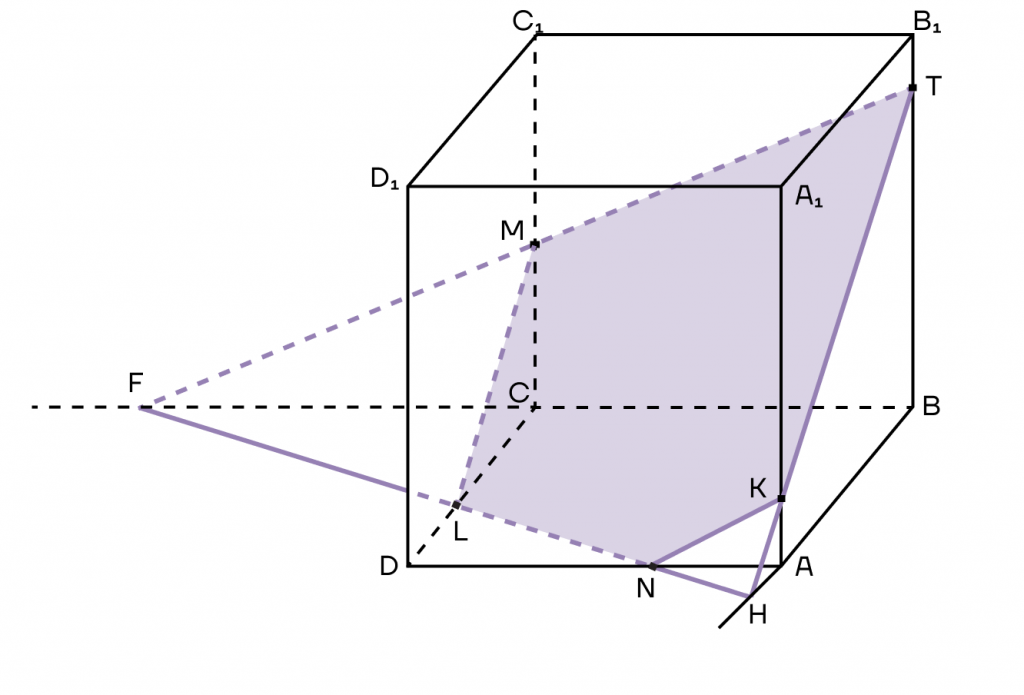
Итак, основной способ построить сечение методом следов — продолжить след сечения до его пересечения с ребрами многогранника или продолжениями его ребер.
А также пользоваться лайфхаком: точки в одной плоскости можно соединять.
Рассмотрим метод внутреннего проектирования.
Иногда метод следов может не помочь: след будет идти параллельно ребру или пересекаться с его продолжением далеко за пределами листа.
В таких случаях часто используется следующее свойство: параллельные плоскости пересекаются другой плоскостью по параллельным прямым. Подробнее про это свойство можно прочесть в статье «Аксиомы стереометрии. Расположение прямых и плоскостей в пространстве».
Польза этого свойства в том, что если сечение пройдет через параллельные плоскости, то оно пересечет их по параллельным линиям. А значит, зная сторону сечения в одной из этих плоскостей и точку в другой плоскости, мы можем просто параллельно перенести прямую и достроить сторону сечения во второй плоскости.
Но будем разбираться на практике. Построим сечение треугольной призмы, проходящее через точки К, М, Т.
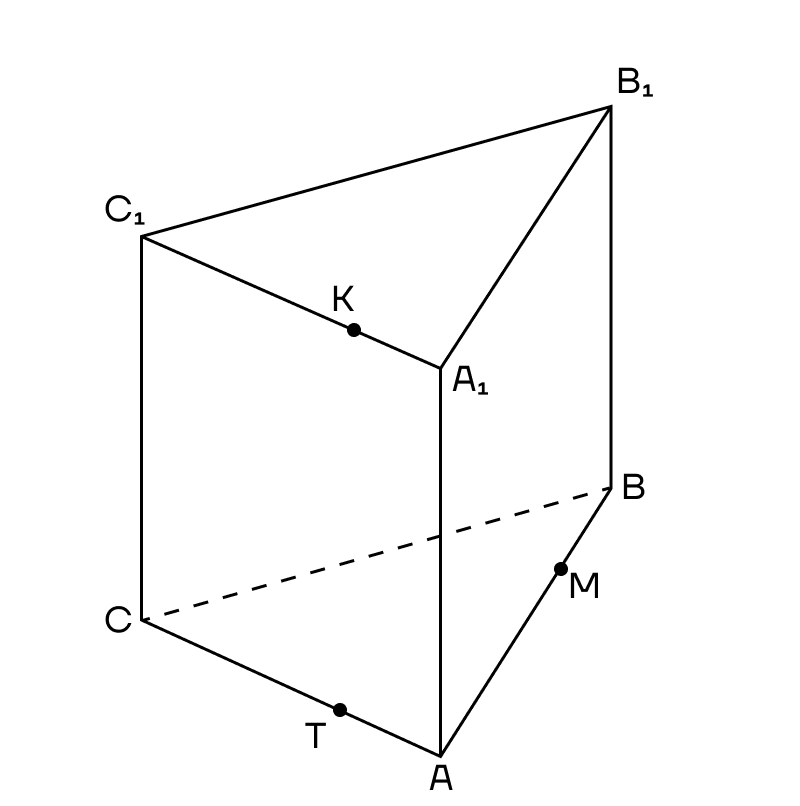
1. Первым делом соединим точки, лежащие в одной плоскости. Это точки К и Т в плоскости (АСС1) и точки Т и М в плоскости (АВС).
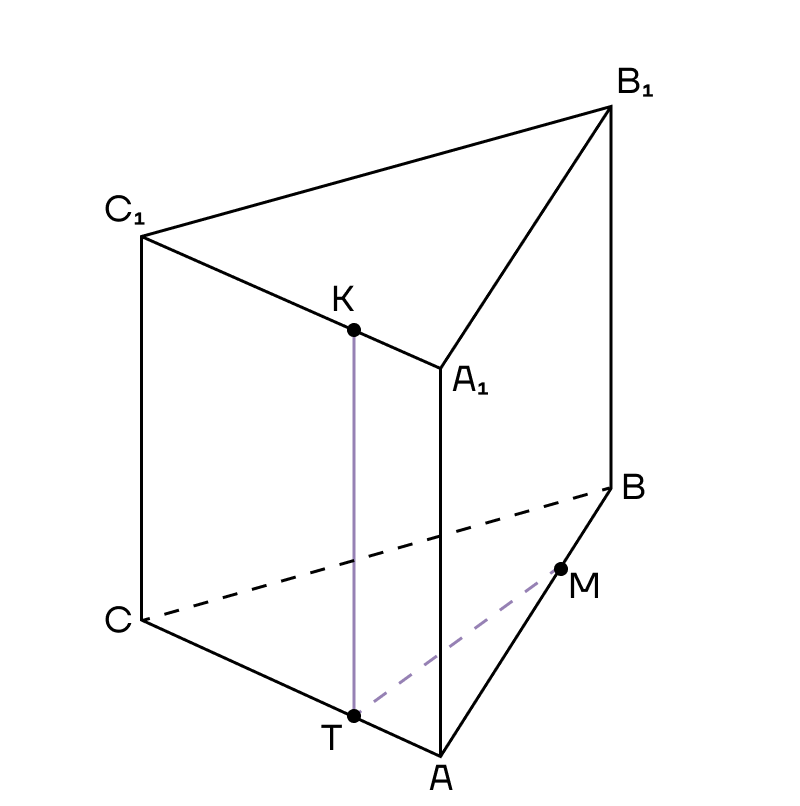
2. КТ проходит почти параллельно ребру АА1, следовательно, использовать метод следов не рационально.
3. Теперь посмотрим на плоскости (АВС) и (А1В1С1) — они параллельные. А значит прямую сечения можно параллельно перенести в одну из них.
В плоскости (АВС) лежит прямая ТМ, а в плоскости (А1В1С1) лежит точка К, которая является вершиной сечения. Тогда из точки К в плоскости верхнего основания нам нужно провести прямую, параллельную ТМ до пересечения с ребром призмы. Назовем эту точку Е.
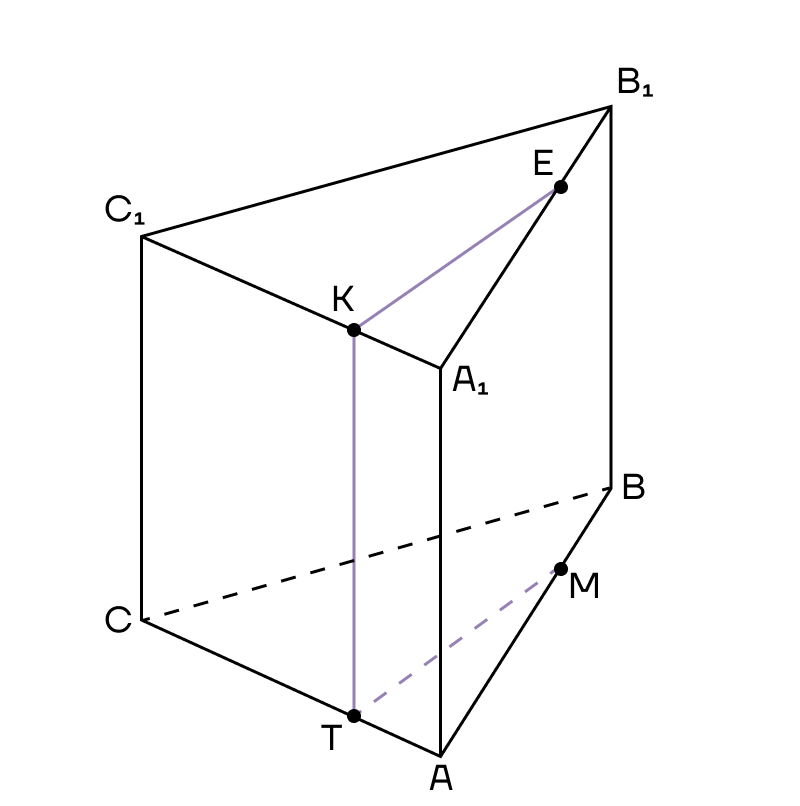
4. А теперь мы можем соединить Е и М, так как они лежат в одной плоскости. Четырехугольник КЕМТ — сечение призмы.
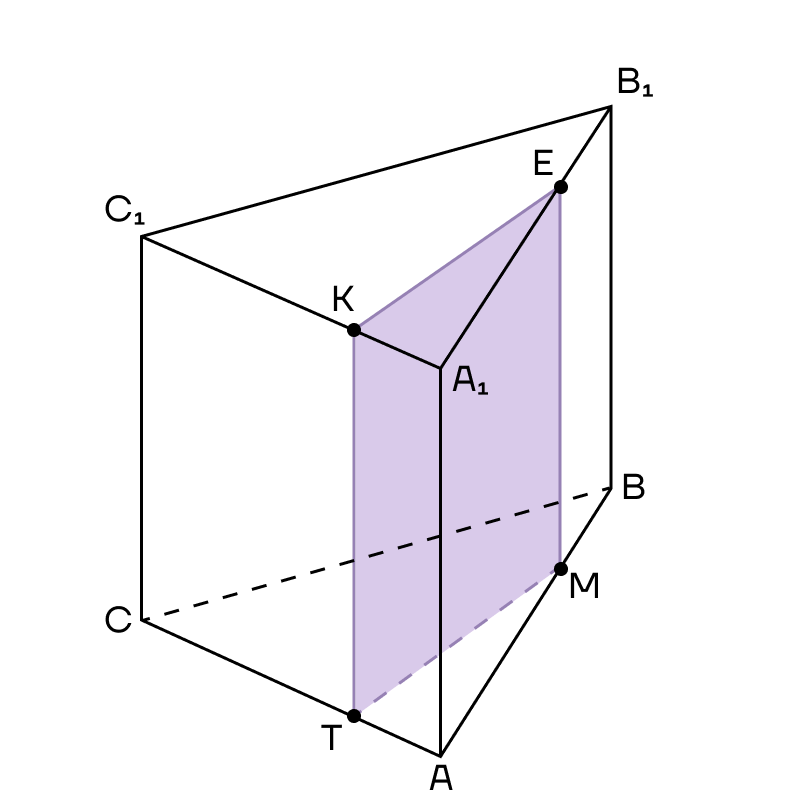
Осталось разобраться, в чем заключается комбинированный метод? Он включает в себя и метод следов, и метод внутреннего проектирования, то есть приемы из каждого метода могут применяться вместе в одной и той же задаче.
Все зависит от удобства решения и его быстроты: там, где невозможно применить метод внутреннего проектирования, можно применить метод следов. А там, где применять метод следов неудобно (или невозможно), можно применить метод внутреннего проектирования.
Примеры построения сечений
Рассмотрим несколько примеров построения сечений в различных фигурах.
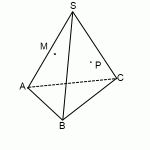
Пример 1. В правильном тетраэдре провели апофему АТ, на середине которой отметили точку К. АЕ:ЕС = 1:5. Р — точка на ребре CD. Постройте сечение тетраэдра, проходящее через точки К, Е и Р.
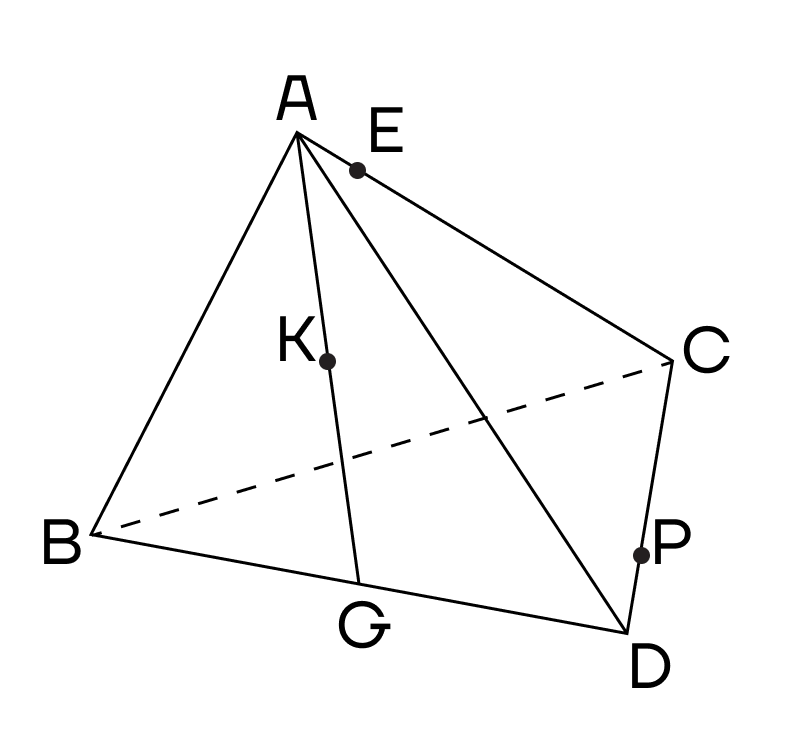
Решение. Подробнее про элементы пирамиды и тетраэдра можно прочесть в статье «Пирамида». Сейчас отметим, что апофема — высота боковой грани правильной пирамиды, проведенная к основанию.
1. Начнем решение с того, что соединим точки, лежащие в одной плоскости. Е и Р лежат в плоскости (ACD), значит их можно соединить.
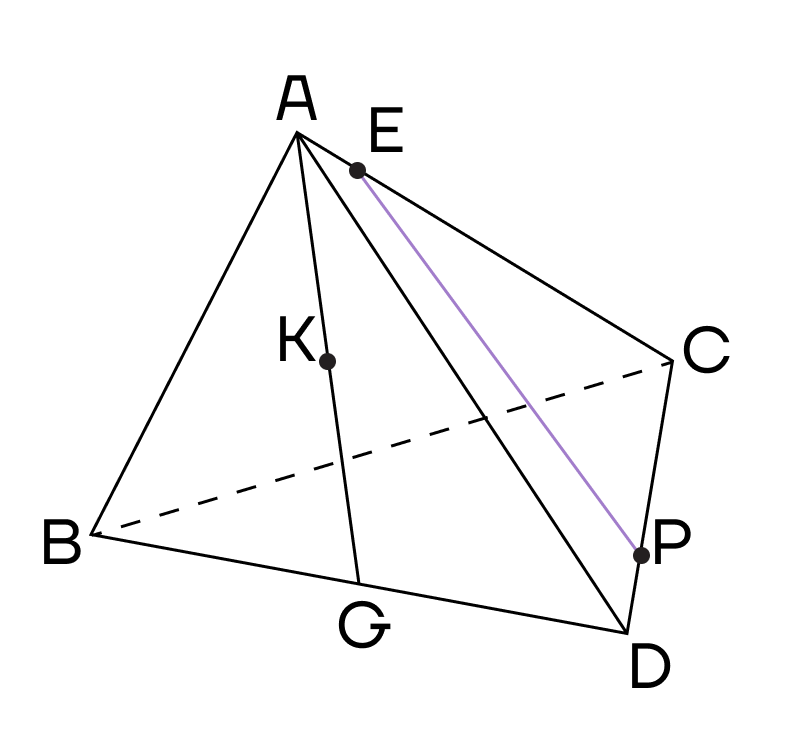
2. Рассмотрим плоскость (АСG). Проведем прямую CG. Точки К и Е лежат в одной плоскости, то есть их также можно соединить.
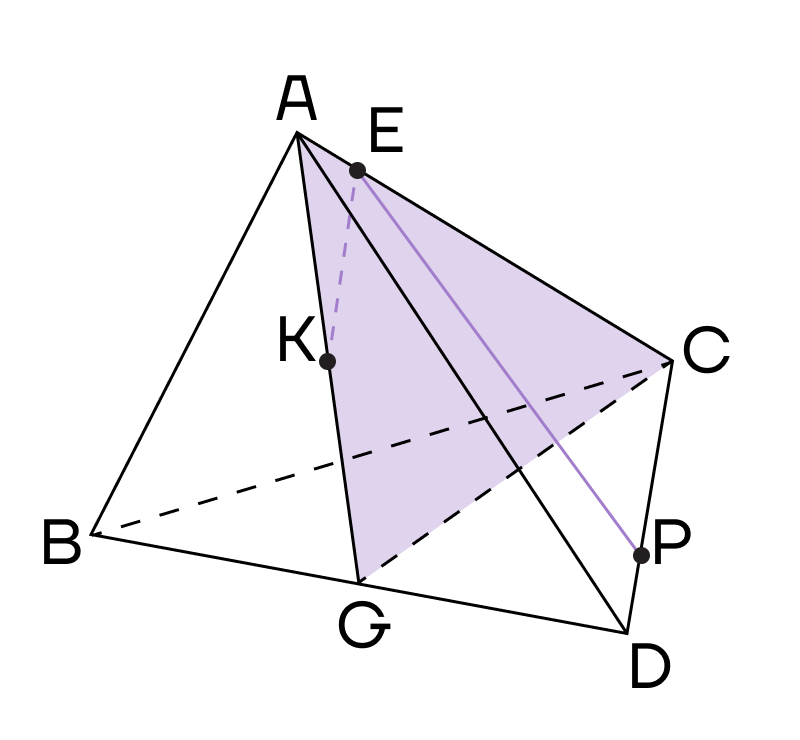
3. Воспользуемся методом следов и продлим прямые ЕК и CG до их пересечения в точке Т.
4. Теперь точки Т и Р будут лежать в одной плоскости основания, следовательно, их можно соединить. Пусть прямая ТР пересекает ребро BD в точке М.
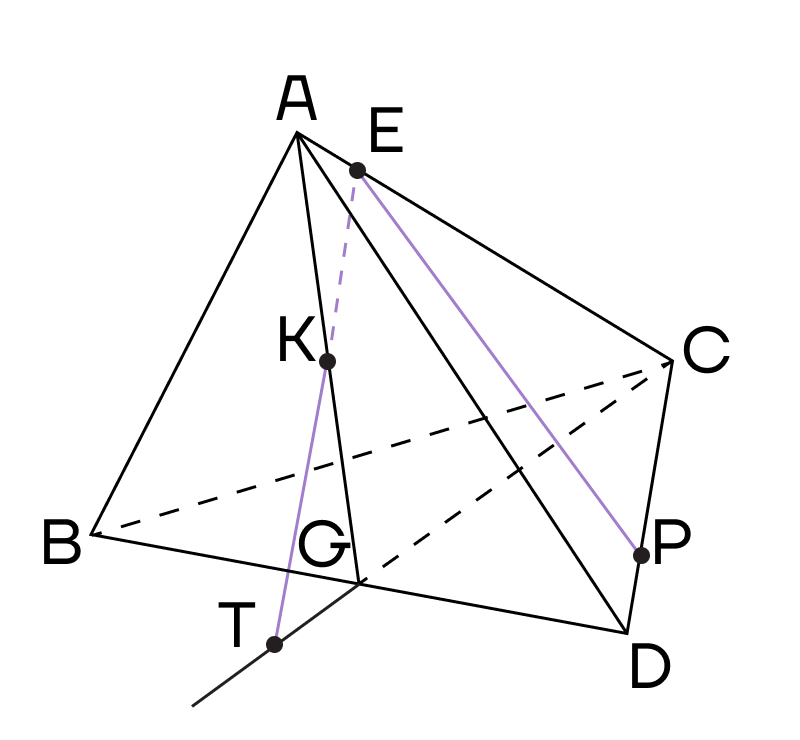
Тогда точки М и К лежат в одной плоскости (ABD) — их тоже можно соединить.
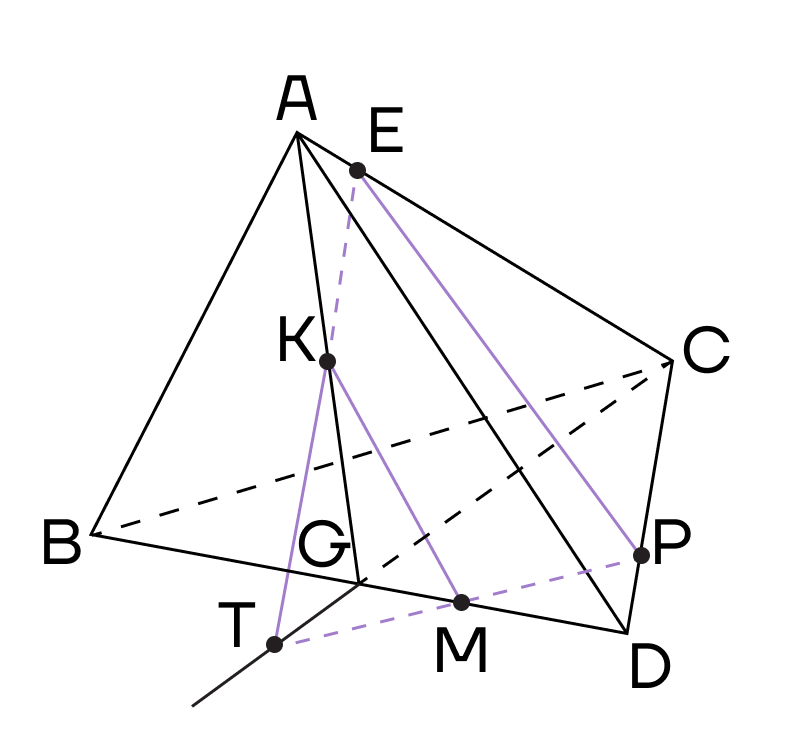
5. Продлим прямую МК до пересечения с ребром АВ в точке О. Точки О и Е лежат в одной плоскости (АВС), соединим их. Сечением тетраэдра будет четырехугольник ОЕРМ.
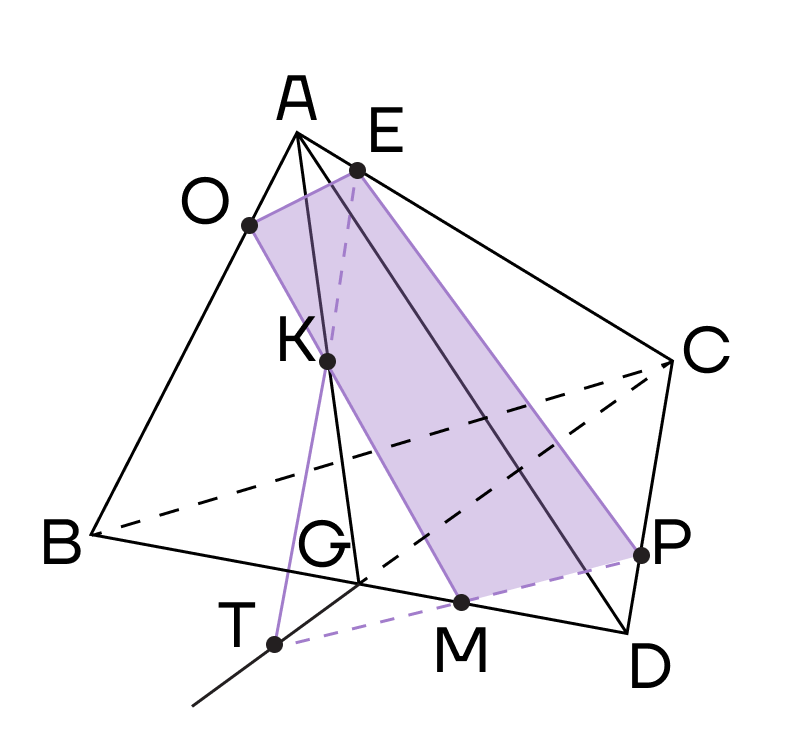
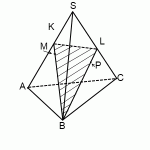
Пример 2. Дана треугольная призма. Постройте сечение призмы, проходящее через точки К, М, Т.
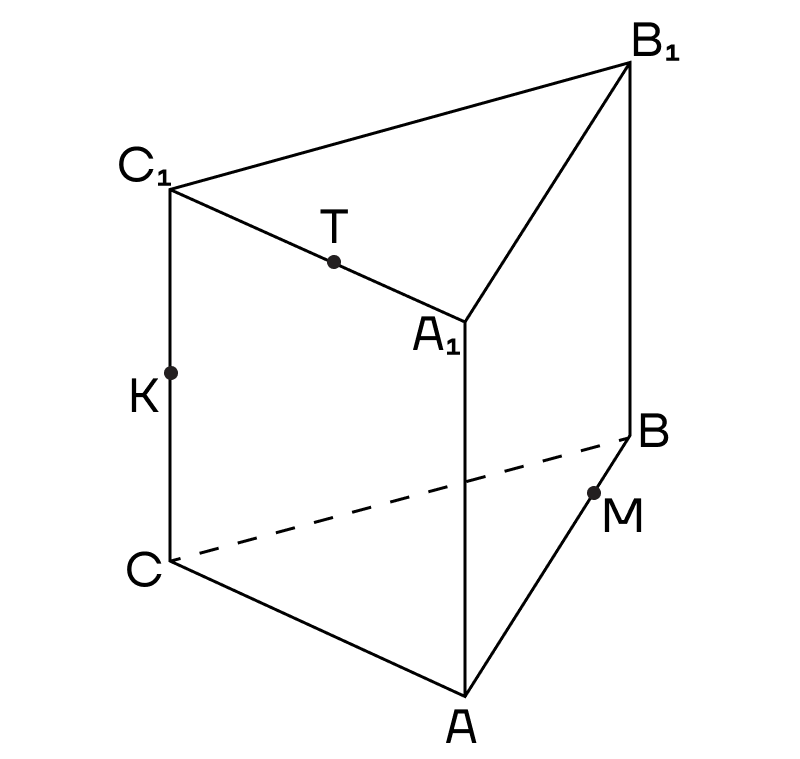
Решение. 1. Соединим точки, лежащие в одной плоскости. Это точки К и Т в плоскости (АСС1).
Воспользуемся методом следов и продолжим прямую ТК до пересечения с продолжением стороны АС в точке Р.
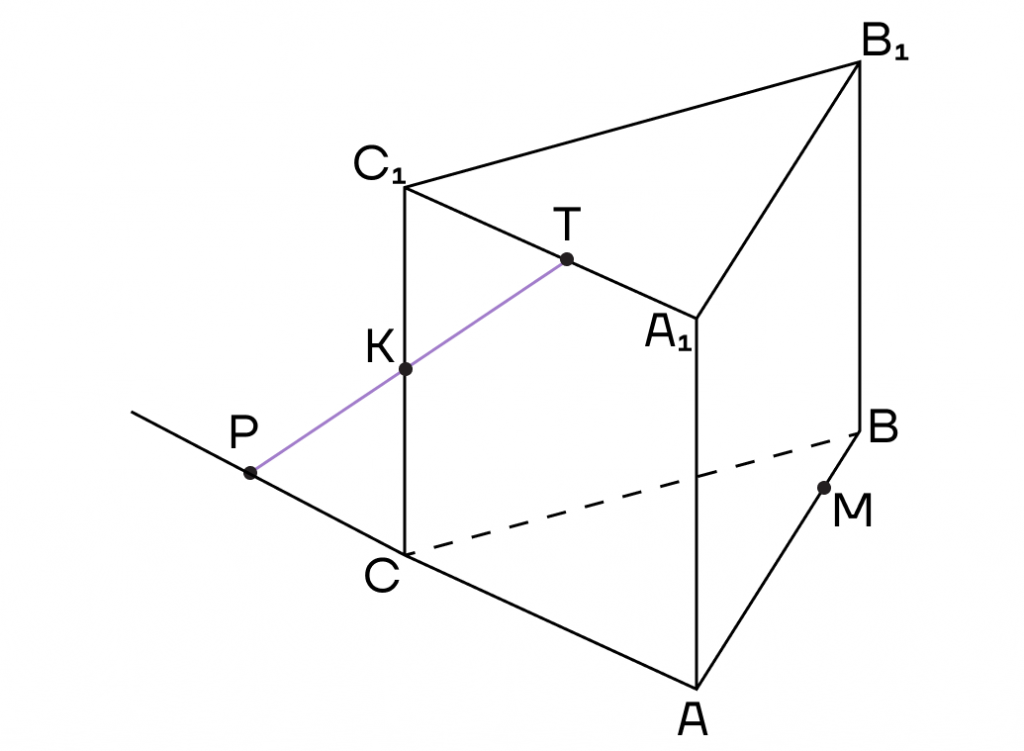
2. Точки Р и М лежат в одной плоскости (АВС), то есть их можно соединить. Пусть прямая РМ пересечет ребро ВС в точке Е.
Воспользуемся методом внутреннего проектирования и проведем из точки Т прямую, параллельную ЕМ. Пусть она пересечет ребро А1В1 в точке О.
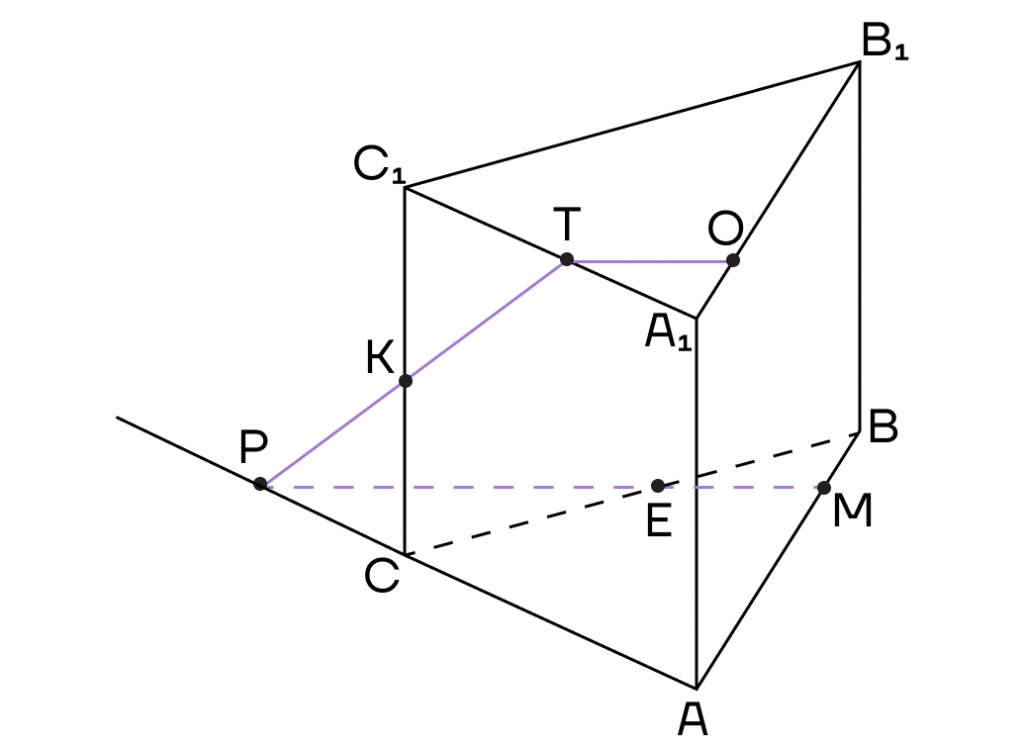
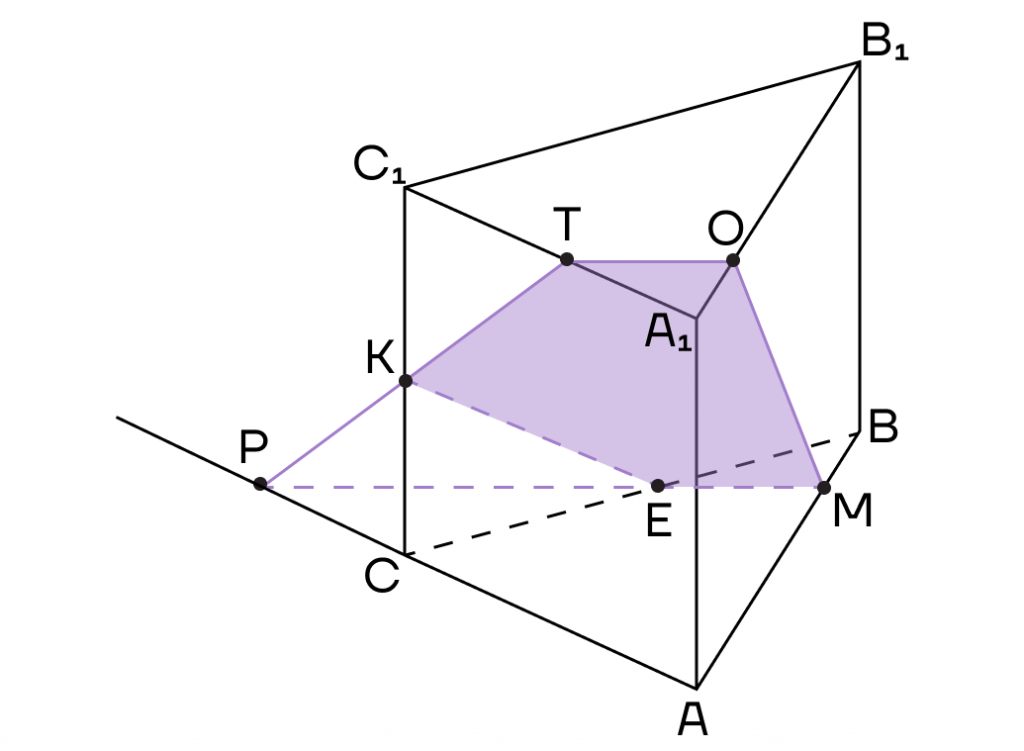
3. Осталось соединить точки, лежащие в одной плоскости. Это точки К и Е в плоскости (ВСС1) и точки О и М в плоскости (АВВ1).
Тогда КТОМЕ — сечение призмы.
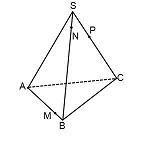
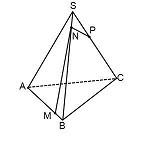
Пример 3. Дан куб ABCDA1B1C1D1. М — середина ребра АА1. Постройте сечение куба, которое будет параллельно диагонали куба А1С и будет проходить через точки М и В.
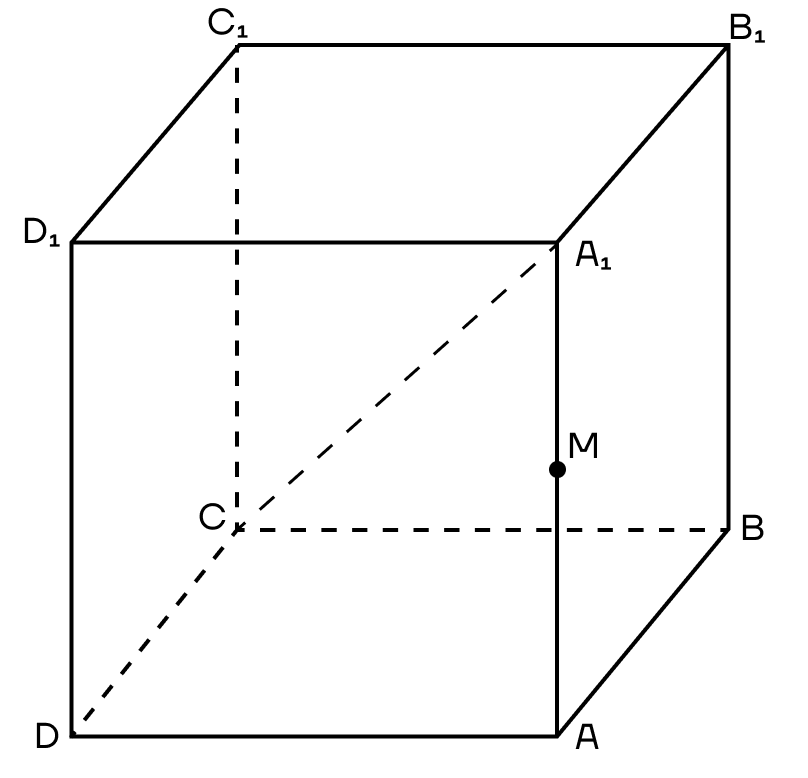
Решение. 1. Достроим прямую АС и рассмотрим плоскость (АА1С). Проведем в ней прямую, параллельную А1С из точки М. Пусть она пересечет АС в точке К.
2. Тогда МК — средняя линия треугольник АА1С, значит К — середина АС.
Подробнее про среднюю линию треугольника можно прочесть в статье «Треугольники».
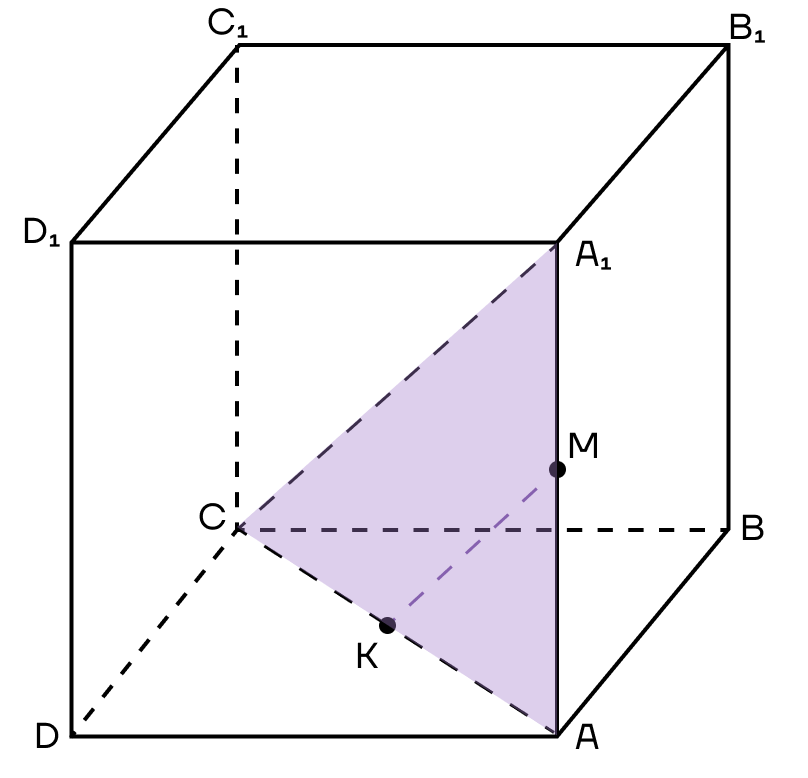
3. Точка К будет принадлежать сечению. Точки В и К лежат в плоскости (АВС) — их можно соединить.
4. В основании куба находится квадрат, его диагонали равны и точкой пересечения делятся пополам.
Подробнее про квадрат и его свойства можно прочитать в статье «Параллелограмм».
Поскольку К — середина диагонали АС, эта же точка будет серединой диагонали BD.
Следовательно, прямую ВК можно продлить до точки D.
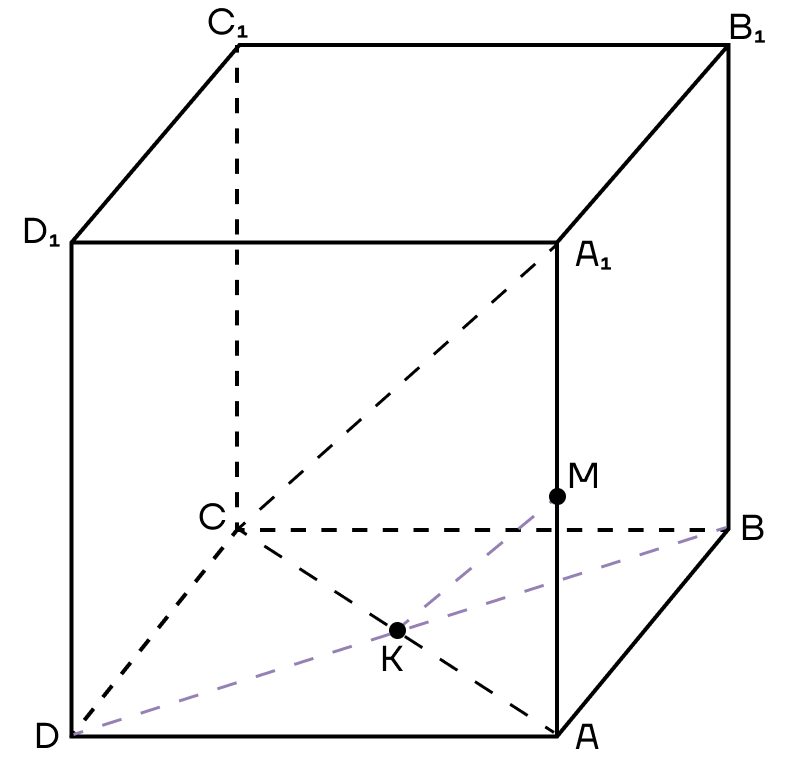
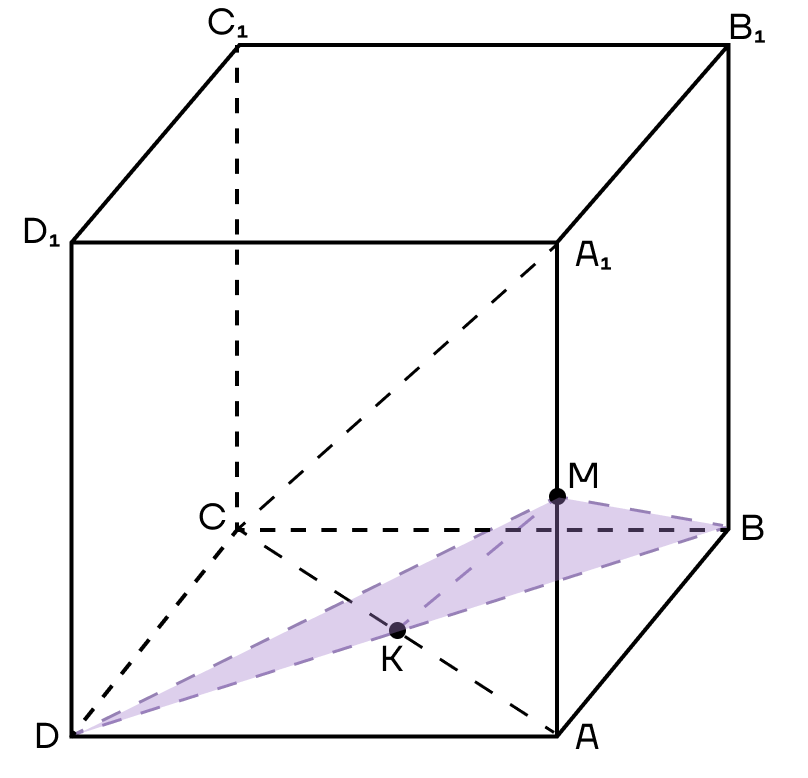
5. Осталось только соединить точки, которые лежат в одной плоскости. Это точки М и D в плоскости (ADD1) и точки М и В в плоскости (ABB1).
Тогда сечением будет треугольник DMB.
Мы рассмотрели сечения и основные способы их построения. В них нет ничего сложного и стоит помнить, что любое сечение можно представить в реальной жизни. Например, попробовать разрезать пластилиновые фигуры.
Фактчек
- Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью. При этом в многогранниках сечения представлены в виде многоугольников, вершины которых лежат на ребрах фигуры.
- Существует несколько методов построения сечения в многогранниках: метод следов, метод внутреннего проектирования и комбинированный метод.
- Метод следов заключается в том, что по следу сечения можно построить его полностью. След сечения — прямая, по которой секущая плоскость пересекает грань многогранника. В методе следов часто нужно продлевать линии и ребра до их пересечения.
- Метод внутреннего проектирования позволяет параллельно переносить сторону сечения в параллельных плоскостях. Это может быть удобно в случаях, когда метод следов невозможно или трудно применить.
- Комбинированный метод — метод, который сочетает в себе и метод следов, и метод внутреннего проектирования.
Проверь себя
Задание 1.
Какая форма сечения будет, если треугольную пирамиду разрезать параллельно основанию?
- Треугольник;
- Четырехугольник;
- Шестиугольник;
- Произвольный многоугольник с любым количеством углов.
Задание 2.
Где могут лежать вершины многоугольника, который образовывает сечение?
- Только в вершинах многогранника;
- На ребрах многогранника;
- Только на гранях многогранника;
- В любой точке на многограннике.
Задание 3.
Что такое след сечения?
- Продолжения сторон сечения;
- Вершины многоугольника, который образовывает сечение;
- Прямая, по которой секущая плоскость пересекает плоскость основания многогранника;
- Все вышеперечисленные варианты.
Задание 4.
Что можно сделать с точками, которые лежат на одной грани?
- Соединить;
- Ни в коем случае нельзя их соединять;
- Построить сечение, опираясь на две разные стороны, не соединяя стороны;
- Ни один из перечисленных вариантов.
Задание 5.
Как можно воспользоваться методом внутреннего проектирования?
- Произвольно переносить линии сечения в любых гранях;
- Произвольно переносить линии сечения в параллельных гранях;
- Перпендикулярно переносить линии сечения в перпендикулярных гранях;
- Параллельно переносить линии сечения в параллельных гранях.
Ответы: 1. — 1 2. — 2 3. — 3 4. — 1 5. — 4
Пошаговое построение сечения четырехугольной пирамиды
Сегодня научимся строить сечения четырехугольной правильной пирамиды. Использовать для построения будем метод следов. Пользоваться этим методом неудобно и даже иногда невозможно, когда сечение имеет малый наклон или не имеет наклона к плоскости основания. Если такой случай вам попадется, лучше использовать метод внутреннего проецирования.
Задача 1.
Построить сечение четырехугольной правильной пирамиды плоскостью, проходящей через точки
.
Задача 1. Дано
Шаг 1. Через точки и
, принадлежащие плоскости грани
, проведем прямую
. Определим точку плоскости основания пирамиды, которая бы принадлежала и секущей плоскости. Для этого проведем продолжение ребра
и найдем точку его пересечения с прямой
— точка
.
Задача 1. Шаг 1.
Шаг 2. Аналогично найдем вторую точку секущей плоскости в плоскости основания: проводим прямую , находим ее пересечение с продолжением ребра
— точка
.
Задача 1. Шаг 2.
Шаг 3. Через две точки можно провести прямую, и, так как точки и
принадлежат и секущей плоскости, и плоскости основания, то и прямая, проведенная через них, будет принадлежать обеим плоскостям. А раз эта прямая лежит в плоскости основания, то определим точки пересечения этой прямой с другими прямыми плоскости основания, например, с продолжением ребра
— точка
, и продолжением ребра
— точка
. Значит, точки
и
— тоже точки плоскости сечения, а за счет того, что прямая
лежит в плоскости грани
, точка
также принадлежит плоскости этой грани. Аналогично, так как прямая
принадлежит плоскости грани
, то и точка
— точка этой же плоскости. Теперь можно соединить точки
и
— как точки одной плоскости, и соединить точки
и
.
Задача 1. Шаг 3.
Шаг 4. Пересечение прямых и
даст нам последнюю точку искомого сечения — точку
.
Задача 1. Шаг 4.
Проводим отрезки ,
, завершая построение:
Многоугольник сечения
Окончательный вид сечения:
Окончательный вид
Задача 2.
Построить сечение четырехугольной правильной пирамиды плоскостью, проходящей через точки
.
Задача 2. Дано
Шаг 1. Проводим прямую , она принадлежит грани
, так как точки
и
принадлежат ей.
Задача 2. Шаг 1.
Шаг 2. Прямая пересечет прямую
, и точка их пересечения
благодаря принадлежности прямой
будет лежать в плоскости основания.
Задача 2. Шаг 2.
Шаг 3. Точки и
принадлежат плоскости основания, проведем через них прямую
, найдем точку пересечения этой прямой ребра
— точку
. Продлим прямую
до пересечения с прямой
, получим точку
. Точка
принадлежит плоскости
, тк как этой плоскости принадлежит прямая
.
Задача 2. Шаг 3.
Шаг 4. Соединим точки и
. Найдем место пересечения данной прямой ребра
— точку
.
Задача 2. Шаг 4.
Шаг 5. Соединяем полученные точки отрезками.
Задача 2. Шаг 5.
Окончательный вид с другого ракурса:
Окончательный вид сечения
Задача 3.
Построить сечение четырехугольной правильной пирамиды плоскостью, проходящей через точки
.
Задача 3. Дано
Шаг 1. Соединим и
, как точки одной плоскости.
Задача 3. Шаг 1.
Шаг 2. Прямая принадлежит плоскости грани
, следовательно, пересечет прямую этой же грани
. Найдем точку их пересечения
, продлив ребро
.
Задача 3. Шаг 2.
Шаг 3. Точки и
— «одного поля ягоды» — обе принадлежат плоскости грани
. Поэтому соединим их, отметив точку пересечения с ребром
—
.
Задача 3. Шаг 3.
Шаг 4. Точки и
принадлежат плоскости основания, соединяем их. Прямая
лежит в плоскости основания и пересечет прямую
в точке
.
Задача 3. Шаги 4-5.
Шаг 5. Точки и
соединяем, так как обе они принадлежат плоскости
, и получаем последнюю точку сечения —
на ребре
.
Шаг 6. Соединяем точки отрезками.
Задача 3. Шаг 6.
Окончательный вид сечения:
Окончательный вид сечения
Задача 4.
Построить сечение четырехугольной правильной пирамиды плоскостью, проходящей через точки
.
Задача 4. Дано.
Шаг 1-2. Точки и
принадлежат грани
, соединим их отрезком (прямой). Точки
и
принадлежат грани основания, также соединим их.
Задача 4. Шаги 1-2
Шаг 3. Прямая пересечет продолжение ребра
в точке
. Точка
, таким образом, принадлежит плоскости грани
.
Задача 4. Шаг 3.
Шаг 4. Соединяем точки и
, проводя прямую
. Она пересечет ребро
в точке
.
Задача 4. Шаг 4.
Шаг 5. Соединяем полученные точки на ребрах отрезками:
Задача 4. Шаг 5.
Окончательный вид с удобного ракурса:
Окончательный вид
4 комментария
Татьяна
✉️
16.07.2020 09:37:47
Пожалуйста, откройте чертежи построения сечения пирамиды.
Анна Валерьевна
✨
17.07.2020 06:13:02
Не поняла Вас, Татьяна: у меня нормально все отображается, все картинки видны.
PitrurlVef
✉️
06.04.2022 13:39:59
TritrurlVef
✉️
08.04.2022 05:52:57
§ 14. Пирамида
14.1. Определение пирамиды и её элементов
Определение. Пирамидой называется многогранник, у которого одна грань — многоугольник, а остальные грани — треугольники с общей вершиной (рис. 95, 96).
Рис. 95
Рис. 96
Многоугольник называется основанием пирамиды, остальные грани — боковыми гранями пирамиды, их общая вершина — вершиной пирамиды. Отрезки, соединяющие вершину пирамиды с вершинами её основания, называются боковыми рёбрами пирамиды.
Пирамиду с основанием АВСDЕ и вершиной Р обозначают PABCDE.
Перпендикуляр, опущенный из вершины пирамиды на плоскость её основания, называется высотой пирамиды. Длину этого перпендикуляра также называют высотой пирамиды.
Пирамида называется n-угольной, если её основанием является n-угольник.
На рисунке 96 изображена четырёхугольная пирамида PABCD, у которой: четырёхугольник ABCD — основание пирамиды; точка Р — вершина пирамиды; отрезки РA, РВ, PC, PD — боковые рёбра пирамиды; отрезки АВ, ВС, CD, DA — стороны (рёбра) основания пирамиды; отрезок РО — высота пирамиды; треугольники РАВ, РВС, PCD, PDA — боковые грани пирамиды.
Рис. 97
У n-угольной пирамиды имеется (n + 1) вершин, 2n рёбер и (n + 1) граней. Диагоналей пирамида не имеет. В пирамиде различают плоские углы при её вершине и двугранные углы при её рёбрах. Двугранным углом при ребре пирамиды называют содержащий пирамиду двугранный угол, образованный плоскостями граней, проходящими через данное ребро.
Треугольную пирамиду (рис. 97) называют также тетраэдром («тетраэдр» по-гречески означает «четырёхгранник»). Тетраэдр — это многогранник с наименьшим числом граней. Любая грань тетраэдра может быть принята за его основание; это отличает тетраэдр от всех остальных пирамид.
Любую пирамиду можно разбить на некоторое число тетраэдров, а любой выпуклый многогранник — на некоторое число пирамид. Для этого достаточно, например, взять любую точку внутри данного многогранника и соединить её отрезками со всеми его вершинами. Такое разбиение часто используется при нахождении объёмов многогранников.
14.2. Некоторые виды пирамид
Если все боковые рёбра пирамиды составляют с плоскостью основания равные углы, то: а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; б) все боковые рёбра пирамиды равны между собой.
Рис. 98
Доказательство. а) Пусть отрезок РО — высота пирамиды PABCDEF, все рёбра которой составляют с плоскостью основания угол ϕ (рис. 98). Тогда прямоугольные треугольники РОА, POB, POC, POD, РОЕ и POF, имея общий катет РО, равны между собой (по катету и острому углу ϕ). Из равенства этих треугольников следует: ОА = OВ = ОС = OD = OE = OF, т. е. вершины основания пирамиды равноудалены от основания О её высоты РО. Это означает, что точка О — центр окружности, описанной около основания ABCDEF данной пирамиды.
б) Из ОА = OВ = ОС = OD = ОЕ = OF следует, что боковые рёбра РА, РВ, PC, PD, РЕ, PF пирамиды равны, как наклонные, имеющие равные проекции, т. е. РА = РВ = PC = PD = РЕ = PF. Что и требовалось доказать. ▼
Вы самостоятельно можете доказать обратные утверждения.
1. Если основание высоты пирамиды совпадает с центром окружности, описанной около её основания, то: а) все боковые рёбра пирамиды образуют с плоскостью основания равные углы; б) все боковые рёбра пирамиды равны между собой.
2. Если все боковые рёбра пирамиды равны, то: а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; б) все боковые рёбра пирамиды составляют с плоскостью её основания равные между собой углы.
Также имеет место следующее утверждение.
Если высота пирамиды пересекает её основание и все боковые грани пирамиды образуют с плоскостью основания равные двугранные углы, то основание высоты пирамиды совпадает с центром окружности, вписанной в её основание.
Доказательство. Пусть РО — высота пирамиды PABCDE, боковые грани которой образуют с плоскостью основания пирамиды двугранные углы, равные ϕ (рис. 99).
Рис. 99
Проведём высоты РН1, РH2, РН3, PH4, РH5 боковых граней.
Тогда по теореме о трёх перпендикулярах получаем OH1 ⟂ AB, OH2 ⟂ BC, OH3 ⟂ CD, OH4 ⟂ DE, OH5 ⟂ EA, следовательно, ∠ OH1P = ∠ OH2P = ∠ OH3P = ∠ OH4P = ∠ OH5P = ϕ. Поэтому △ OH1P = △ OH2P = △ OH3P = △ OH4P = △ OH5P (как прямоугольные с общим катетом OP и острым углом ϕ). Из равенства этих треугольников следует ОН1 = OH2 = OH3 = ОН4 = ОН5, т. е. точка О — основание высоты РО пирамиды — равноудалена от всех сторон многоугольника ABCDE. Это означает, что точка O является центром окружности, вписанной в основание ABCDE данной пирамиды. Теорема доказана. ▼
Самостоятельно докажите обратное утверждение.
Если вершина пирамиды проектируется в центр окружности, вписанной в основание пирамиды, то боковые грани пирамиды образуют с плоскостью основания равные двугранные углы.
Перечислим ещё несколько часто встречающихся в задачах видов пирамид.
Рис. 100
Рис. 101
Рис. 102
• Пирамида, ровно одна боковая грань которой перпендикулярна плоскости основания. Высота такой пирамиды лежит в этой, перпендикулярной основанию, грани (рис. 100).
• Пирамида, две соседние боковые грани которой перпендикулярны плоскости основания. Высотой такой пирамиды служит боковое ребро, общее для этих граней (рис. 101).
• Пирамида, две не соседние боковые грани которой перпендикулярны плоскости основания. Высота такой пирамиды лежит на прямой пересечения плоскостей этих граней (рис. 102).
14.3. Правильная пирамида
Определение. Пирамида называется правильной, если её основание — правильный многоугольник и вершина пирамиды проектируется в центр этого основания.
Рис. 103
Из определения следует алгоритм построения изображения правильных пирамид, что, в свою очередь, доказывает существование таких пирамид.
Для построения изображения правильной пирамиды достаточно построить изображение соответствующего правильного многоугольника (основания пирамиды) и его центра. Затем из построенного центра провести перпендикуляр к плоскости многоугольника и выбрать на этом перпендикуляре (в качестве вершины пирамиды) любую точку, отличную от центра многоугольника. Соединив отрезками прямых эту точку со всеми вершинами многоугольника, получим изображение правильной пирамиды.
На рисунке 103, а, б, в построены изображения правильных пирамид: а) треугольной; б) четырёхугольной; в) шестиугольной.
Правильные пирамиды обладают замечательным свойством.
В правильной пирамиде все боковые рёбра равны, а все боковые грани — равные равнобедренные треугольники.
Рис. 104
Доказательство. Рассмотрим правильную n-угольную пирамиду РА1А2…An. Пусть точка O — центр n-угольника A1A2A3…An; отрезок РО — перпендикуляр к плоскости основания пирамиды (рис. 104).
Так как центр правильного многоугольника является центром окружности, описанной около этого многоугольника, то ОА1 = OA2 = OA3 = … = OAn (как радиусы описанной окружности). Тогда равны боковые рёбра пирамиды, как наклонные к плоскости её основания, имеющие равные проекции, т. е. PA1 = PA2 = PA3 = … = PAn.
Таким образом, имеем:
РА1 = РA2 = … = PAn (как боковые рёбра);
A1A2 = A2A3 = … = AnA1 (как стороны правильного n-угольника).
Следовательно, треугольники PA1A2, РA2A3, …, PAnA1 являются равнобедренными и по третьему признаку равенства треугольников равны между собой.
Это свойство правильной пирамиды можно доказать при помощи поворота пирамиды вокруг оси, содержащей её высоту.
Так как точка О — центр правильного n-угольника A1A2A3…An, лежащего в основании правильной пирамиды PA1A2…An, РО — перпендикуляр к плоскости её основания, то при вращении данной пирамиды вокруг оси ОР на угол, равный 
Следствием доказанного выше является утверждение.
Все боковые рёбра правильной пирамиды образуют с плоскостью основания равные углы, а все боковые грани — равные двугранные углы.
Докажите это предложение самостоятельно.
Высота боковой грани правильной пирамиды, проведённая к ребру её основания, называется апофемой пирамиды. На рисунке 104 отрезок РН — одна из апофем пирамиды.
Все апофемы правильной пирамиды равны вследствие равенства всех её боковых граней.
Имеют место признаки правильной пирамиды:
Пирамида, в основании которой лежит правильный многоугольник, является правильной, если: а) все её боковые рёбра равны; б) все её боковые рёбра образуют с плоскостью основания равные углы; в) все её боковые грани — равные равнобедренные треугольники.
Докажите это самостоятельно.
ЗАДАЧА (2.245). Высота правильной четырёхугольной пирамиды равна h и образует с боковой гранью угол α. Через сторону основания пирамиды проведена плоскость, перпендикулярная противоположной грани и пересекающая её. Найти площадь сечения.
Дано: PABCD — правильная пирамида (рис. 105); РО — высота пирамиды, РО = h; ∠ OPF = α.
Найти: SADKM.
Решение. Первый способ. Пусть отрезок EF — средняя линия основания пирамиды. Тогда AD ⟂ EF, AD ⟂ PF ⇒ АD ⟂ (РEF) ⇒ (PEF) ⟂ (ADP) (по признаку перпендикулярности двух плоскостей). Поэтому прямая PF является ортогональной проекцией прямой РO на плоскость ADP. Значит, ∠ OPF — угол между высотой PO и боковой гранью ADP пирамиды: ∠ OPF = α.
Рис. 105
Далее имеем: AD ⟂ (PEF), ВС || AD ⇒ ВC ⟂ (PEF) ⇒ прямая ВС перпендикулярна любой прямой плоскости PEF. Поэтому если FL ⟂ РЕ (в плоскости PEF), то BС ⟂ FL. Тогда FL ⟂ ВС, FL ⟂ PE ⇒ FL ⟂ (BCP) ⇒ (ADL) ⟂ (ВCР) (по признаку перпендикулярности двух плоскостей); при этом (ADL) ∩ (ВСР) = МK, МK || AD, так как плоскости ВСР и АDL проходят через параллельные прямые ВС и AD. Значит, сечение ADKM — трапеция, у которой FL — высота (почему?), откуда
Sсеч = 
Найдём AD, МK и FL.
В △ OPF (∠ POF = 90°):
OF = OP•tg α = h•tg α; PF = 

Поэтому
EF = 2FO = 2h•tg α = ВС.
В плоскости PEF получаем:
FL ⟂ РЕ, РО ⟂ EF ⇒ ∠ EFL = ∠ OPE = α.
Тогда в △ ЕFL: FL = ЕF•cos α = 2h•tg α•cos α = 2hsin α;
в △ PLF (∠ PLF = 90°, ∠ PFL = 90° – 2α):
PL = PF•sin (90° – 2α) = PF•cos 2α = 
Так как MK | | BC, то △ МKР ∾ △ ВСР, откуда




= 2htg α•cos 2α.
Таким образом,
AD = EF = 2h•tg α, FL = 2h•sin α, MK = 2h•tg α•cos 2α.
Тогда
Sсеч = 

= 
Замечание. Отрезок MK можно найти следующим образом. Сечением данной пирамиды плоскостью, проходящей через прямую MK параллельно основанию пирамиды, является квадрат MKD1A1 (см. рис. 105). F1 = A1D1 ∩ PF. У этого квадрата LF1 = MK. Найдём F1L.
В треугольнике LFF1 имеем ∠ FLF1 = α (LF1 || EF),
∠ F1FL = ∠ OFP – ∠ OFL = (90° – α) – α = 90° – 2α;
∠ FF1L = 180° – ∠ OFF1 = 90° + α. Тогда по теореме синусов
Рис. 106
Значит, MK = LF1 = 2h•tg α•cos 2α.
Второй способ. Пусть точки M1, K1, L1 — ортогональные проекции на плоскость основания соответственно точек М, K, L (рис. 105, 106). Так как плоскости АСР, BDP и EFP перпендикулярны плоскости основания пирамиды, то ортогональными проекциями прямых PC, РВ и РЕ на эту плоскость являются соответственно прямые АС, BD и EF. Следовательно, M1 ∈ BD, K1 ∈ AC, L1 ∈ EF, причём четырёхугольник ADK1M1 — равнобедренная трапеция.
Таким образом, трапеция ADK1M1 — ортогональная проекция сечения ADKM. Это означает, что SADKM = 





Тогда
SADKM = 

Ответ: 4h2•sin2 α•cos α.
14.4.Площади боковой и полной поверхностей пирамиды
Поверхность пирамиды состоит из основания и боковых граней. В этой связи различают боковую и полную поверхности пирамиды, а также их площади.
Площадью боковой поверхности пирамиды (обозначают Sбок) называется сумма площадей всех её боковых граней: Sбок = S1 + S2 + … + Sn, где S1, S2, …, Sn — площади боковых граней пирамиды.
Площадью полной поверхности пирамиды (обозначают Sполн) называется сумма площадей всех её граней, т. е. сумма площади основания пирамиды и площади её боковой поверхности.
Из определения следует: Sполн = Sбок + Sосн.
О площади боковой поверхности правильной пирамиды имеет место следующая теорема.
Теорема 18. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему пирамиды.
Рис. 107
Доказательство. PA1A2…An — правильная пирамида, a — длина её апофемы (рис. 107).
Боковые грани правильной пирамиды — равные равнобедренные треугольники, у которых основаниями являются стороны правильного n-угольника A1A2…An, а высоты равны апофеме пирамиды, т. е.
РE1 = РE2 = PE3 = … = PEn = a.
Тогда
Sбок = S△PA1A2 + S△PA2A3 + … + S△PAnA1 =
= 


= 

где Р — периметр основания пирамиды. Теорема доказана. ▼
Теорема 19. Если все боковые грани пирамиды наклонены к плоскости основания под углом ϕ и высота пересекает основание, то Sбок = 
Рис. 108
Доказательство. Пусть отрезок PO — высота пирамиды РA1A2A3…An, все боковые грани которой образуют с плоскостью основания углы, равные ϕ (рис. 108); отрезки PH1, PH2, …, PHn — высоты боковых граней. Тогда (по теореме о трёх перпендикулярах) OH1 ⟂ A1A2, OH2 ⟂ A2A3, …, OHn ⟂ AnA1. Значит,
∠ OH1P = ∠ OH2P = ∠ OH3P = …
… = ∠ OHnP = ϕ.
Так как точка О является центром круга, вписанного в основание пирамиды (почему?), то эта точка лежит внутри n-угольника A1A2A3…An. Поэтому n-угольник A1A2…An является объединением непересекающихся треугольников A1OA2, A2OA3, …, AnOA1. Эти треугольники являются ортогональными проекциями на плоскость основания пирамиды её соответствующих боковых граней. По теореме о площади ортогональной проекции многоугольника имеем:
S△ A1OA2 = S△ A1PA2•cos ϕ,
S△ A2OA3 = S△ A2PA3•cos ϕ,
…………………………….
S△ AnOA1 = S△ AnPA1•cos ϕ.
Сложив почленно эти равенства, получим Sосн = Sбок•cos ϕ, откуда Sбок = 
Так как все боковые грани правильной пирамиды образуют с плоскостью основания равные двугранные углы (пусть величина этих углов равна ϕ, см. рис. 107), то для площади боковой поверхности и площади основания правильной пирамиды также справедлива формула
Sбок = 
14.5. Свойства параллельных сечений пирамиды
Если плоскость α параллельна основанию пирамиды и пересекает её, то в сечении пирамиды получается некоторый многоугольник (рис. 109).
Теорема 20. Если пирамида пересечена плоскостью, параллельной основанию, то: 1) боковые рёбра и высота делятся этой плоскостью на пропорциональные части; 2) в сечении получается многоугольник, подобный основанию; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Доказательство. 1) Пусть сечением пирамиды PABCD плоскостью α, параллельной плоскости β её основания, является четырёхугольник A1B1C1D1 (см. рис. 109).
Рис. 109
Проведём высоту РО данной пирамиды и обозначим O1 = РО ∩ α.
Рассмотрим гомотетию 
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия 
Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:





где k — коэффициент гомотетии 
Вследствие того, что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии, а k = РO1 : РО, где РO1 и РО — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
SA1B1C1D1 : SABCD = k2 = 
Теорема доказана. ▼
Следствие. Плоскость, параллельная основанию пирамиды и пересекающая её, отсекает пирамиду, подобную данной.
14.6. Усечённая пирамида
Плоскость α, параллельная основанию пирамиды PABCD и пересекающая её, делит эту пирамиду на два многогранника: пирамиду РA1B1C1D1 и многогранник ABCDA1B1C1D1 (см. рис. 109).
Рис. 110
Многогранник ABCDA1B1C1D1 (рис. 110) называют усечённой пирамидой. Грани ABCD и A1B1C1D1, лежащие в параллельных плоскостях, называются соответственно нижним и верхним основаниями усечённой пирамиды, остальные грани — её боковыми гранями. Так как нижнее и верхнее основания усечённой пирамиды гомотетичны (т. 20), то все её боковые грани — трапеции.
Таким образом, усечённой пирамидой называется часть полной пирамиды, заключённая между её основанием и параллельным ему сечением.
У n-угольной усечённой пирамиды 2n вершин, 3n рёбер, (n + 2) грани и n(n – 3) диагоналей.
Высотой усечённой пирамиды называется перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённой пирамиды. На рисунке 110 отрезки О1О, B1K — высоты усечённой пирамиды.
Рис. 111
Усечённая пирамида называется правильной, если она получена из правильной пирамиды (рис. 111).
Из теоремы 20 следует, что основания правильной усечённой пирамиды — подобные правильные многоугольники, а боковые грани — равные равнобедренные трапеции.
Высоты этих трапеций, соединяющие середины их оснований, называются апофемами усечённой пирамиды. Все её апофемы равны между собой.
Отрезок OO1, соединяющий центры оснований правильной усечённой пирамиды, является её высотой.
Площадью боковой поверхности усечённой пирамиды называется сумма площадей всех её боковых граней.
Для правильной усечённой пирамиды имеет место
Теорема 21. Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров её оснований на апофему.
Для доказательства теоремы достаточно площадь одной из боковых граней пирамиды умножить на их число. В результате получим формулу Sбок = 
Проведите доказательство теоремы самостоятельно.
Полная поверхность усечённой пирамиды — это объединение её оснований и боковой поверхности, поэтому для усечённой пирамиды
Sполн = Sбок + S1 + S2,
где S1 и S2 — площади большего и меньшего оснований этой пирамиды.
Для усечённой пирамиды, у которой все двугранные углы при рёбрах большего основания равны ϕ, справедливо: Sбок = 

14.7. Объём пирамиды
Лемма. Две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики.
Доказательство. Пусть пирамиды РАВС и P1A1B1C1 имеют высоты, равные H, и равновеликие основания с площадью S; их объёмы — соответственно V1 и V2. Докажем, что V1 = V2.
Расположим пирамиды РАВС и P1A1B1C1 так, чтобы их основания лежали в одной плоскости, а сами пирамиды были расположены по одну сторону от этой плоскости (рис. 112). Тогда любая плоскость, параллельная плоскости оснований и пересекающая первую пирамиду, пересекает и вторую, причём по теореме о параллельных сечениях пирамиды площади этих сечений равны. Следовательно, на основании принципа Кавальери равны и объёмы этих пирамид. Лемма доказана. ▼
Рис. 112
Теорема 22. Объём любой треугольной пирамиды равен одной трети произведения площади основания на высоту.
Рис. 113
Доказательство. Пусть А1AВC — данная треугольная пирамида с вершиной A1 и основанием ABC (рис. 113). Дополним эту пирамиду до треугольной призмы ABCA1B1C1 с тем же основанием, одним из боковых рёбер которой является боковое ребро АA1 данной пирамиды. Это означает, что высота призмы равна высоте данной пирамиды.
Призма АВCA1B1C1 является объединением трёх треугольных пирамид с общей вершиной A1: A1ABC, A1BB1C1 и A1BCC1. Основания BB1C1 и BCC1 пирамид A1BB1C1 и A1BCC1 равны, а высота у них общая. Значит, по лемме эти пирамиды имеют равные объёмы.
Будем считать точку В вершиной пирамиды A1BB1C1, a △ A1B1C1 — её основанием. Тогда эта пирамида равновелика пирамиде А1AВС, так как у них общая высота, а основания АВС и A1B1C1 равновелики (как основания призмы). Таким образом, призма ABCA1B1C1 является объединением трёх равновеликих пирамид, одной из которых является данная пирамида A1ABC. Это означает, что объём V пирамиды A1АВС составляет одну треть объёма призмы ABCA1B1C1, т. е. V = 
V = 
где Н — длина высоты данной пирамиды. Теорема доказана. ▼
Рис. 114
На рисунке 114 изображены треугольная призма ABCDEF и составляющие её три равновеликие треугольные пирамиды ABDF, ABCF и BDEF.
Рис. 115
Для вычисления объёма n-угольной пирамиды PA1A2…An (рис. 115) разобьём её основание A1A2…An диагоналями A1A3, A1A4, …, A1An – 1 на треугольники с общей вершиной A1. Тогда данная пирамида разбивается в объединение пирамид PA1A2A3, PA1A3A4, …, PA1An – 1An с общей вершиной Р и общей высотой, которая равна высоте данной пирамиды. Основаниями этих пирамид являются треугольники разбиения основания данной пирамиды. Это означает (свойство 2 объёмов), что объём V пирамиды PA1A2…An равен сумме объёмов V1, V2, …, Vn – 2 треугольных пирамид соответственно PA1A2A3, PA1A3A4, …, PA1An – 1An.
Пусть длина высоты пирамиды равна Н, площадь её основания — S, а площади треугольников разбиения этого основания равны S1, S2, …, Sn – 2. Это означает, что S1 + S2 + … + Sn – 2 = S. Тогда получаем:
V = V1 + V2 + … + Vn – 2 = 

Таким образом, объём любой пирамиды вычисляется по формуле
V = 
где Sосн — площадь основания, Н — длина высоты пирамиды.
Итак, доказана теорема.
Теорема 23. Объём любой пирамиды равен одной трети произведения площади основания на высоту. ▼
14.8. Об объёме тетраэдра
У тетраэдра за основание можно принять любую его грань, на каждую из которых можно провести высоту тетраэдра из вершины, противоположной этой грани. Поэтому для объёма V одного и того же тетраэдра имеют место соотношения
V = 



где Sk и hk (k = 1, 2, 3, 4) — площадь грани и длина опущенной на неё высоты. Эти соотношения часто используют при решении задач.
Заметим, что не в любом тетраэдре все четыре высоты пересекаются в одной точке (для сравнения — все три высоты любого треугольника пересекаются в одной точке). Тетраэдр, все высоты которого пересекаются в одной точке, называется ортоцентрическим.
Интересен также тетраэдр (рис. 116, а), все грани которого равны. Такой тетраэдр называется равногранным. Его развёрткой является остроугольный треугольник (рис. 116, б).
Докажите самостоятельно, что в равногранном тетраэдре:
—скрещивающиеся рёбра попарно равны;
—все высоты равны;
—сумма плоских углов трёхгранного угла при каждой вершине тетраэдра равна 180°;
—двугранные углы при скрещивающихся рёбрах тетраэдра равны.
Рис. 116
Рис. 117
Не менее интересен следующий факт. Пусть дан тетраэдр A1C1BD. Проведём через каждое его ребро плоскость, параллельную скрещивающемуся с ним ребру. Проведённые шесть плоскостей при пересечении образуют некоторый параллелепипед АВСDA1В1C1D1 (рис. 117), параллельные грани ABCD и A1B1C1D1 которого содержат скрещивающиеся рёбра А1C1 и BD данного тетраэдра. Тогда расстояние между основаниями АВСD и А1В1С1D1 полученного параллелепипеда равно длине его высоты и равно расстоянию между скрещивающимися рёбрами А1C1 и BD данного тетраэдра.
Этот параллелепипед можно разбить на пять тетраэдров — данный тетраэдр A1С1ВD и ещё четыре тетраэдра: A1ABD; ВВ1A1C1; C1CBD; DD1A1C1. Объём каждого из четырёх последних тетраэдров равен одной трети высоты h параллелепипеда, умноженной на половину площади его основания ABCD, т. е. шестой части объёма V полученного параллелепипеда.
Таким образом,
где ϕ — угол между диагоналями АС и BD параллелограмма ABCD. А так как AC || A1C1, то величина угла между скрещивающимися диагоналями A1С1 и BD тетраэдра А1С1BD также равна ϕ.
Мы получили: объём тетраэдра равен одной шестой произведения длин любых двух его скрещивающихся рёбер, расстояния между ними и синуса угла между скрещивающимися прямыми, содержащими эти рёбра.
Отметим ещё несколько очевидных и менее очевидных свойств тетраэдров, связанных с их объёмами.
1. Объёмы тетраэдров с равными основаниями относятся как их высоты, опущенные на эти основания.
Рис. 118
2. Объёмы тетраэдров с равными высотами относятся как площади их оснований.
3. Объёмы тетраэдров, имеющих равные трёхгранные углы, относятся, как произведения длин рёбер, образующих эти углы.
Используя рисунок 118, вы сможете легко доказать третье утверждение.
14.9. Объём усечённой пирамиды
Теорема 24. Объём усечённой пирамиды, у которой площади оснований равны S1 и S2, а высота — Н, вычисляется по формуле
V = 

Рис. 119
Доказательство. Пусть дана усечённая пирамида (рис. 119), у которой S1 > S2, а высота OO1 = H. Дополним эту пирамиду до полной пирамиды с вершиной Р. Объём V данной усечённой пирамиды равен разности объёмов полной и дополнительной пирамид.
Если длина высоты PO1 дополнительной пирамиды равна x, то высота PO полной пирамиды равна H + x.
Выразим х через S1, S2 и Н. По теореме 20 (o площадях параллельных сечений пирамиды) имеем
S1 : S2 = (H + x)2 : x2 ⇒ 

⇒
x = 
Поэтому для объёма V усечённой пирамиды находим
что и требовалось доказать. ▼
Содержание
- Узнать ещё
- Как построить сечение пирамиды
- Задание 3. Многогранники
- 4.1. Краткие теоретические сведения
- 4.2. Способ перемены плоскостей проекций
- 4.3. Развертывание поверхностей
- 4.4. Задание 3. Построение натурального вида сечения пирамиды плоскостью
- 4.4.1. Условие задания
- 4.4.2. Рекомендации по выполнению задания № 2
- Видеопример выполнения задания №3
- 4.5. Варианты задания 3
Узнать ещё
Знание — сила. Познавательная информация
Как построить сечение пирамиды
Разберем, как построить сечение пирамиды, на конкретных примерах. Поскольку в пирамиде нет параллельных плоскостей, построение линии пересечения (следа) секущей плоскости с плоскостью грани чаще всего предполагает проведение прямой через две точки, лежащие в плоскости этой грани.
В простейших задачах требуется построить сечение пирамиды плоскостью, проходящей через данные точки, уже лежащие в одной грани.
Построить сечение плоскостью (MNP)
Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.
Треугольник MNP — сечение пирамиды
Точки M и N лежат в одной плоскости ABS, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, значит, соединяем M и N сплошной линией.
Точки M и P лежат в одной плоскости ACS, поэтому через них проведем прямую. След — отрезок MP. Мы его не видим, поэтому отрезок MP проводим штрихом. Аналогично строим след PN.
Треугольник MNP — искомое сечение.
Если точка, через которую требуется провести сечение, лежит не на ребре, а на грани, то она не будет концом следа-отрезка.
Пример. Построить сечение пирамиды плоскостью, проходящей через точки B, M и N, где точки M и N принадлежат, соответственно, граням ABS и BCS.
Здесь точки B и M лежат в одной грани ABS, поэтому можем через них провести прямую.
Аналогично проводим прямую через точки B и P. Получили, соответственно, следы BK и BL.
Точки K и L лежат в одной грани ACS, поэтому через них можем провести прямую. Ее след — отрезок KL.
Треугольник BKL — искомое сечение.
Однако не всегда через данные в условии точки удается провести прямую. В этом случае нужно найти точку, лежащую на прямой пересечения плоскостей, содержащих грани.
Пример. Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.
Точки M и N лежат в одной плоскость ABS, поэтому через них можно провести прямую. Получаем след MN. Аналогично — NP. Оба следа видимые, поэтому соединяем их сплошной линией.
Точки M и P лежат в разных плоскостях. Поэтому соединить их прямой не можем.
Продолжим прямую NP.
Она лежит в плоскости грани BCS. NP пересекается только с прямыми, лежащими в этой же плоскости. Таких прямых у нас три: BS, CS и BC. С прямыми BS и CS уже есть точки пересечения — это как раз N и P. Значит, ищем пересечение NP с прямой BC.
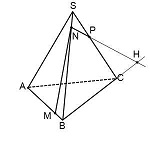
Эта точка H принадлежит как плоскости (BCS), поскольку лежит на прямой NP, так и плоскости (ABC), поскольку лежит на прямой BC.
Таким образом мы получили еще одну точку секущей плоскости, лежащей в плоскости (ABC).
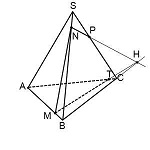
Получим след MT.
T — точка пересечения прямых MH и AC.
Так как T принадлежит прямой AC, то через нее и точку P можем провести прямую, так как они обе лежат в одной плоскости (ACS).
4-угольник MNPT — искомое сечение пирамиды плоскостью, проходящей через данные точки M,N,P.
Мы работали с прямой NP, продлевая ее для отыскания точки пересечения секущей плоскости с плоскостью (ABC). Если работать с прямой MN, приходим к тому же результату.
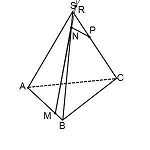
Значит, продлевая MN, ищем точку пересечения ее с прямой AS. Назовем эту точку R.
Точка R лежит на прямой AS, значит, она лежит и в плоскости (ACS), 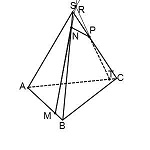
Поскольку точка P лежит в плоскости (ACS), через R и P можем провести прямую. Получаем след PT.
Точка T лежит в плоскости (ABC), поэтому через нее и точку M можем провести прямую.
Таким образом, получили все то же сечение MNPT.
Рассмотрим еще один пример такого рода.
Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.
Через точки M и N, лежащие в одной плоскости (BCS), проводим прямую. Получаем след MN (видимый).
Через точки N и P, лежащие в одной плоскости (ACS), проводим прямую. Получаем след PN (невидимый).
Через точки M и P прямую провести не можем.
1) Прямая MN лежит в плоскости (BCS), где есть еще три прямые: BC, SC и SB. С прямыми SB и SC уже есть точки пересечения: M и N. Поэтому ищем точку пересечения MN с BC. Продолжив эти прямые, получаем точку L.
Точка L принадлежит прямой BC, а значит, она лежит в плоскости (ABC). Поэтому через L и P, которая также лежит в плоскости (ABC) можем провести прямую. Ее след — PF.
F лежит на прямой AB, а значит, и в плоскости (ABS). Поэтому через F и точку M, которая также лежит в плоскости (ABS), проводим прямую. Ее след — FM. Четырехугольник MNPF — искомое сечение.
2) Другой путь — продолжить прямую PN. Она лежит в плоскости (ACS) и пересекается с прямыми AC и CS, лежащими в этой плоскости, в точках P и N.
Значит, ищем точку пересечения PN с третьей прямой этой плоскости — с AS. Продолжаем AS и PN, на пересечении получаем точку E. Поскольку точка E лежит на прямой AS, принадлежащей плоскости (ABS), то через E и точку M, которая также лежит в (ABS), можем провести прямую. Ее след — FM. Точки P и F лежат водной плоскости (ABC), проводим через них прямую и получаем след PF (невидимый).
Источник
Задание 3. Многогранники
4.1. Краткие теоретические сведения
Многогранниками называются тела, ограниченные плоскими n-угольниками, которые называются гранями . Линии пересечения граней называются ребрами , точки пересечения ребер – вершинами. Для всех многогранников справедлива формула Эйлера: сумма граней и вершин за минусом числа ребер есть величина постоянная: Г + В – Р = 2.
Наиболее распространенными в технике многогранниками являются правильные и неправильные, прямые и наклонные призмы и пирамиды. Призмой называется многогранник, в основании которого находится плоский n-угольник, а остальные грани являются в общем случае параллелограммами. Пирамидой называется многогранник, в основании которого находится плоский n-угольник, а боковыми гранями являются треугольники с общей вершиной. На эпюре многогранники задаются проекциями ребер, так называемой сеткой ребер .
Типовой задачей для многогранников является задача о пересечении многогранников плоскостями частного и общего положения. Для построения фигуры сечения многогранника плоскостью используют следующие приемы:
-
- определение каждой вершины сечения, как точки пересечения ребер многогранника с секущей плоскостью ( способ ребер );
- построение стороны сечения, как линии пересечения с секущей плоскостью граней многогранника ( способ граней ).
Чаще применяется первый из заданных приемов, второй же целесообразно применять в тех случаях, когда грани многогранника являются проецирующими плоскостями, линии пересечения которых с секущей плоскостью общего положения строятся очень просто.
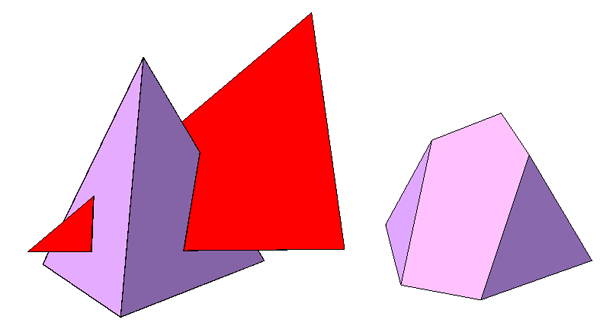
а б
Рисунок 4.1 – Пересечение пирамиды плоскостью (а — задание, б — результат)
В методе ребер несколько раз (по числу пересекаемых ребер) решается задача о пересечении прямой (ребра) с плоскостью (секущей плоскостью). В этом случае находятся точки 1, 2, 3 (рис. 4.1). Найденные точки являются вершинами сечения пирамиды плоскостью.
В методе граней несколько раз решается типовая задача о пересечении двух плоскостей (граней многогранника и секущей плоскости), в которой находят линии 1-2, 2-3, 3-1, являющиеся сторонами многоугольника (в данном примере, треугольника сечения). Если секущая плоскость является плоскостью частного положения, то задача решается упрощенно.
4.2. Способ перемены плоскостей проекций
Сущность способа перемены плоскостей проекций заключается в том, что положение геометрических элементов (точек, прямых, фигур, тел) в пространстве остается неизменным, а система плоскостей проекций заменяется новой, по отношению к которой эти элементы занимают положение, наиболее удобное для решения той или иной задачи.
В ряде случаев для решения задачи бывает достаточно заменить новой плоскостью одну из основных плоскостей проекций – фронтальную или горизонтальную. В других же случаях замена лишь одной плоскости проекций вопроса не разрешает и бывает необходимо последовательно заменить новыми плоскостями обе основные плоскости проекций.
При замене основной плоскости проекций новой плоскостью эта последняя должна располагаться по отношению к остающейся основной плоскости проекций перпендикулярно.
Рассмотрим способ перемены плоскостей проекций на примерах.
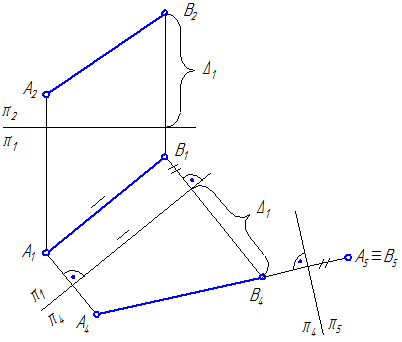
Для того чтобы данная прямая общего положения m=АВ оказалась линией уровня, следует ввести новую плоскость проекций π4, которая была бы ей параллельна (рис. 4.2 и 4.3).
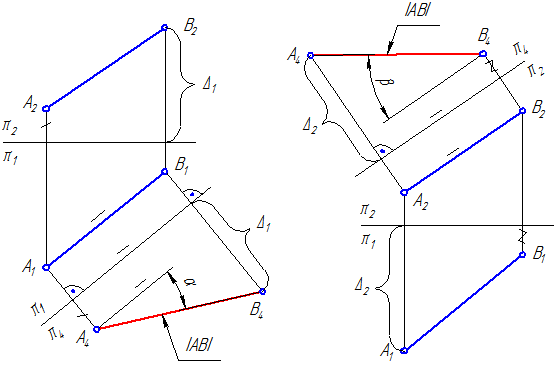
Рисунок 4.2 Рисунок 4.3
На Рисунке 4.2 введена плоскость π4, параллельная прямой m и перпендикулярная к плоскости π1; по новым линиям связи от оси π1/π4 откладываем расстояния от точек А и В до плоскости π1 (отмеченное штрихом и D1). В новой системе плоскостей проекций π1/π4 прямая m является линией уровня.
На Рисунке 4.3 плоскость π4 параллельна прямой m=АВ и перпендикулярна к плоскости π2. Прямая m в системе π2/π4 является линией уровня.
Для того чтобы прямая линия была проецирующей прямой вводится плоскость проекций, перпендикулярная к ней. Для прямой общего положения требуется провести две замены плоскостей проекций. На Рисунке 4.4 прямая m=АВ спроецирована на параллельную ей плоскость π4. Затем вводится плоскость проекций π5, перпендикулярная m4. В системе плоскостей проекций π5/π4 прямая m проецируется в точку.
Рисунок 4.4 – Проецирование отрезка прямой в точку
Чтобы определить натуральную величину плоской фигуры общего положения (Рисунок 4.5), требуется сначала ввести такую плоскость проекций π4, чтобы образовалась система, в которой плоскость α, заданная треугольником АВС будет проецирующей. Данную подзадачу можно решить, введя дополнительную плоскость проекций π4 перпендикулярно либо горизонтальной проекции горизонтали, либо фронтальной проекции фронтали. Затем вводится дополнительная плоскость π5, перпендикулярная к плоскости π4 и параллельная плоскости α .
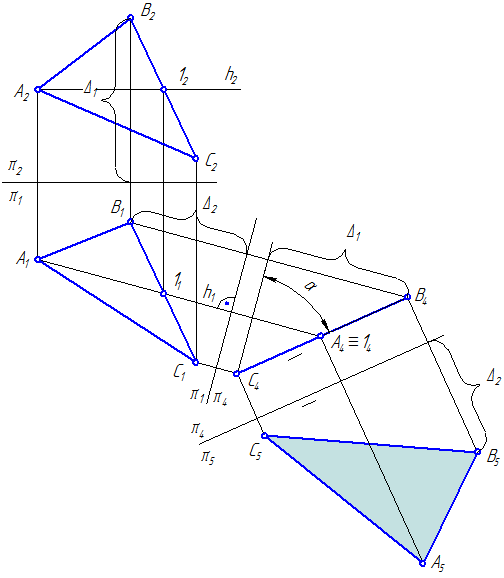
Рисунок 4.5 – Определение натуральной величины треугольника
4.3. Развертывание поверхностей
Разверткой называется плоская фигура, получаемая путем совмещения с плоскостью чертежа поверхности тела.
Построение разверток имеет большое значение в таких областях техники, как котлостроение, судостроение, кровельное и жестяночное дело, продукция которых изготовляется из листового материала.
Точные развертки могут быть построены лишь для линейчатых поверхностей, смежные положения образующих которых параллельны (цилиндрическая поверхность) или пересекаются (коническая поверхность).
Для нелинейчатых поверхностей, образующей которых является кривая линия (например, сферическая поверхность), можно построить развертки лишь приближенные. С этой целью такие поверхности разбиваются на небольшие элементы, и каждая такая часть кривой поверхности заменяется плоскостью. Это означает, что данная кривая поверхность заменяется вписанным в нее многогранником, развертка которого приближенно принимается за развертку кривой поверхности.
Развертка боковой поверхности пирамиды (Рисунок 4.7) состоит из трех треугольников, представляющих в истинном виде боковые грани пирамиды.
Для построения развертки необходимо предварительно определить истинные длины боковых ребер пирамиды. Повернув эти ребра вокруг высоты пирамиды до положения параллельного плоскости ?2, на фронтальной плоскости проекций получим их истинные длины в виде отрезков S2 A 2, S2 B 2, S2 C 2 (Рисунок 4.6).
Построив по трем сторонам S2 A 2, S2 B 2 и A1B1 грань пирамиды ASB (Рисунок 4.7), пристраиваем к ней смежную грань – треугольник BSC, а к последнему – грань CSA. Полученная фигура представит собою развертку боковой поверхности данной пирамиды.
Для получения полной развертки к одной из сторон основания пристраиваем основание пирамиды – треугольник АВС.
Для построения на развертке линии, по которой поверхность пирамиды пересечется плоскостью α (Рисунок 4.7), следует нанести на ребра SA, SB и SC, соответственно, точки 1, 2 и 3, в которых эта плоскость пересекает ребра, определив истинные длины отрезков S1, S2 и S3.
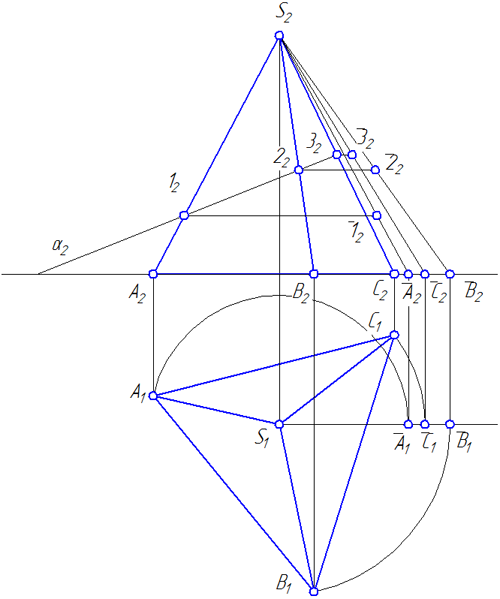
Рисунок 4.6 – Определение истинных длин ребер 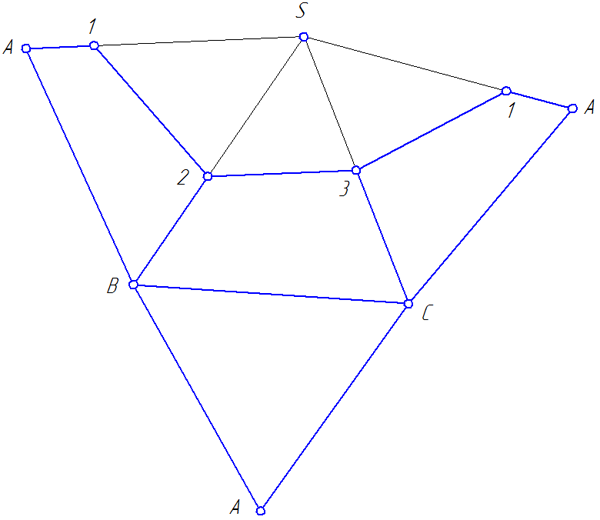
Рисунок 4.7 – Построение развертки
4.4. Задание 3. Построение натурального вида сечения пирамиды плоскостью
4.4.1. Условие задания
Задание следует выполнять в соответствии с алгоритмом:
-
- По координатам вершин (Таблицы 3.1- 3.3) построить: две проекции пирамиды 1234S;
-
- Выполнить две проекции сечения пирамиды плоскостью общего положения АВС (Таблица 3.4);
-
- Найти натуральный вид сечения способом перемены плоскостей проекций;
- Выполнить развертку верхней отсеченной части пирамиды.
4.4.2. Рекомендации по выполнению задания № 2
Порядок выполнения задачи следующий:
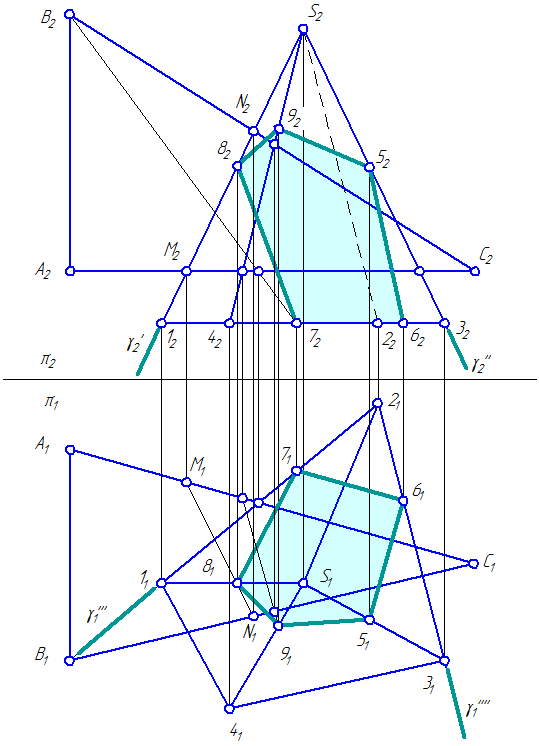
- Построить горизонтальные и фронтальные проекции пирамиды и 1234S и плоскости ∆АBC (Рисунок 4.8);
- Способом ребер или способом граней построить проекции сечения пирамиды 1234S плоскостью ∆АBC.
Способ ребер заключается в том, что ребро пирамиды (например, 1S) заключается во фронтально-проецирующую плоскость γ: γπ2≡12S2. Затем выполняется построение точки 8 пересечения ребра 1S с плоскостью γ:
Аналогично выполняется построение остальных точек искомого сечения.
Способом граней строятся линии пересечения с помощью плоскостей-посредников;
Рисунок 4.8 – Построение сечения
- Способом перемены плоскостей проекций найти натуральный вид сечения 56789.
Сущность способа перемены плоскостей проекций состоит в том, что положение геометрического образа (прямой, плоскости, поверхности) в пространстве остается неизменным, а система плоскостей проекций π1/π2 дополняется плоскостями, образующими с π1 или π2, либо между собой системы двух взаимно перпендикулярных плоскостей проекций. Расположение новой плоскости проекций по отношению к геометрическим образам выбирается в зависимости от условия задачи.
В данной задаче необходимо дважды ввести новые плоскости проекций: в системе плоскостей π1/π4 сечение 56789 станет проецирующей плоскостью, а в системе плоскостей проекций π4/π5 – плоскостью уровня;
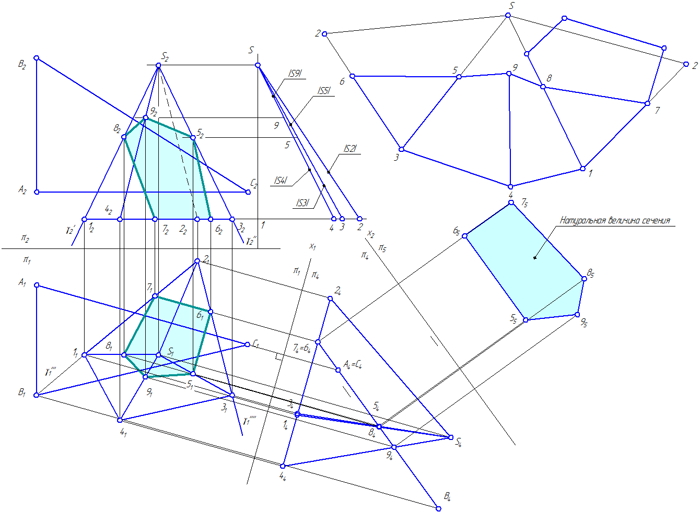
Рисунок 4.9 – Пересечение пирамиды плоскостью общего положения
- Выполнить развертку нижней отсеченной части пирамиды.
Видеопример выполнения задания №3
4.5. Варианты задания 3
Таблица 3.1– Значения координат точек (для вариантов с 1 по 10)
| S | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| X | 50 | 90 | 30 | 10 | 70 |
| Y | 50 | 50 | 5 | 70 | 80 |
| Z | 90 | 10 | 10 | 10 | 10 |
Таблица 3.2– Значения координат точек (для вариантов с 11 по 20)
| S | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| X | 50 | 90 | 30 | 10 | 70 |
| Y | 50 | 50 | 5 | 70 | 80 |
| Z | 90 | 0 | 0 | 0 | 0 |
Таблица 3.3– Значения координат точек (для вариантов с 21 по 30)
| S | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| X | 50 | 100 | 25 | 5 | 80 |
| Y | 50 | 50 | 5 | 70 | 80 |
| Z | 100 | 10 | 10 | 10 | 10 |
Таблица 3.4– Значения координат точек
| Вариант | Координаты (x, y, z) точек | Вариант | Координаты (x, y, z) точек | ||||
|---|---|---|---|---|---|---|---|
| А | В | С | А | В | С | ||
| 1 | 100;15;30 | 35; 85; 90 | 10; 45; 30 | 16 | 90; 0; 0 | 100; 50; 70 | 5; 55; 40 |
| 2 | 65; 10; 0 | 100; 50; 80 | 20; 80; 80 | 17 | 95; 35; 40 | 50; 35; 0 | 5; 65; 50 |
| 3 | 100; 25;40 | 15; 90; 90 | 50; 15; 0 | 18 | 50; 50; 45 | 0; 55; 0 | 100; 20; 5 |
| 4 | 30; 80; 90 | 20; 25; 0 | 100; 25; 40 | 19 | 30; 90; 60 | 90; 30; 20 | 0; 35; 0 |
| 5 | 100; 15; 20 | 100; 60; 90 | 10; 45; 20 | 20 | 95; 15; 0 | 5; 60; 20 | 70; 85; 80 |
| 6 | 90; 0; 0 | 100; 50; 80 | 5; 55; 40 | 21 | 100;15;30 | 35; 85; 90 | 10; 45; 30 |
| 7 | 95; 35; 50 | 50; 35; 0 | 5; 65; 50 | 22 | 65; 10; 0 | 100; 50; 80 | 20; 80; 80 |
| 8 | 50; 50; 55 | 0; 55; 5 | 100; 20; 5 | 23 | 100; 25;40 | 15; 90; 90 | 50; 15; 0 |
| 9 | 30; 90; 70 | 90; 30; 30 | 0; 35; 0 | 24 | 30; 80; 90 | 20; 25; 0 | 100; 25; 40 |
| 10 | 95; 15; 10 | 5; 60; 30 | 70; 85; 80 | 25 | 100; 15; 20 | 100; 60; 90 | 10; 45; 20 |
| 11 | 100;15;20 | 35; 85; 80 | 10; 45; 30 | 26 | 90; 0; 0 | 100; 50; 80 | 5; 55; 40 |
| 12 | 65; 10; 0 | 100; 50; 70 | 20; 80; 80 | 27 | 95; 35; 50 | 50; 35; 0 | 5; 65; 50 |
| 13 | 100; 25;30 | 15; 90; 80 | 50; 15; 0 | 28 | 50; 50; 55 | 0; 55; 5 | 100; 20; 5 |
| 14 | 30; 80; 80 | 20; 25; 0 | 100; 25; 40 | 29 | 30; 90; 70 | 90; 30; 30 | 0; 35; 0 |
| 15 | 100; 15; 10 | 100; 60; 80 | 10; 45; 20 | 30 | 95; 15; 10 | 5; 60; 30 | 70; 85; 80 |
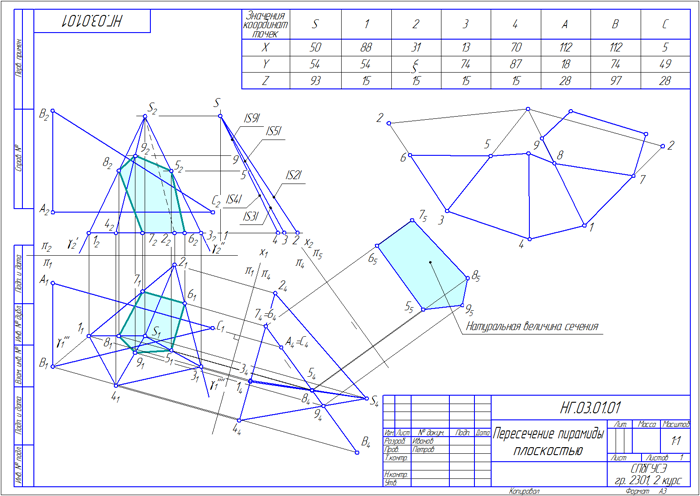
Рисунок 4.10 – Пример оформления задания 3
Источник