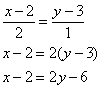Как найти перпендикулярную линию

Did this article help you?

Уравнение перпендикулярной прямой

Альтернативная формула
Прямая, проходящая через точку M₁(x₁; y₁) и перпендикулярная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения перпендикулярной прямой (см. также как составить уравнение параллельной прямой).

Пример №1 . Составить уравнение прямой, проходящей через точку (2; -1) и перпендикулярной 4x-9y=3 .
Решение. Данную прямую можно представить уравнением y = 4 /₉x – 1 /₃ (a = 4 /₉). Уравнение искомой прямой есть y+1 = -9/4(x-2) , т.е. 9x+4y-14=0 .

Пример №2 . Решая пример 1 (A=4, B=-9) по формуле (2), найдем 4(y+1)+9(x-2)=0 , т.е. 9x+4y-14=0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-3, -2) перпендикулярно прямой 2y+1=0 .
Решение. Здесь A=0, B=2. Формула (2) дает -2(x+3)=0, т.е. x+3=0 . Формула (1) неприменима, так как a=0 .

Уравнение перпендикулярной прямой

Как составить уравнение прямой перпендикулярной данной прямой и проходящей через данную точку?

Пусть y=k₁x+b₁ — данная прямая. С учётом условия перпендикулярности прямых уравнение прямой, перпендикулярной данной, имеет вид

Если эта прямая проходит через точку M(x_o; y_o), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение x_o и y_o, мы найдем b.

1) Написать уравнение прямой, проходящей через точку A(-10;3), перпендикулярной прямой y=5x-11.

Так как прямые перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, то

Значит уравнение прямой, перпендикулярной прямой y=5x-11, имеет вид

Так как прямая проходит через точку A(-10;3), то координаты A удовлетворяют уравнению прямой:

Итак, уравнение прямой, перпендикулярной прямой y=5x-11 и проходящей через точку A(-10;3)

2) Написать уравнение прямой, перпендикулярной прямой x= -2, проходящей через точку M(-5;9).

Прямая x= -2 перпендикулярна оси абсцисс. Значит, прямая, уравнение которой мы ищем, параллельна оси абсцисс, то есть ищем уравнение прямой в виде y=b.

Так как искомая прямая проходит через точку M(-5;9), то координаты M удовлетворяют уравнению прямой: y=9.

3) Написать уравнение прямой, перпендикулярной прямой y=4, проходящей через точку F(7;-5).

Прямая y=4 перпендикулярна оси ординат. Следовательно, прямая, уравнение которой мы ищем, параллельна оси ординат, а значит, её уравнение имеет вид x=a.

Так как эта прямая проходит через точку F(7;-5), то координаты F удовлетворяют уравнению прямой: x=7.

Уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой

В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.

Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой

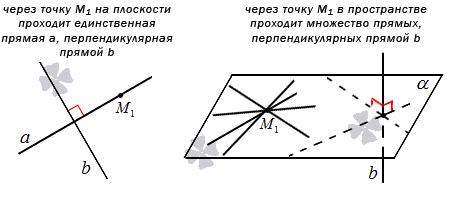
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.

Если плоскость α проходит через заданную точку М 1 перпендикулярно к заданной прямой b , то прямые, лежащие в этой плоскости, в том числе и проходящая через М 1 являются перпендикулярными заданной прямой b .

Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.

Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.

Если на плоскости с системой координат О х у z имеем прямую b , то ей соответствует уравнение прямой на плоскости, задается точка с координатами M 1 ( x 1 , y 1 ) , а необходимо составить уравнение прямой a , которая проходит через точку М 1 , причем перпендикулярно прямой b .

По условию имеем координаты точки М 1 . Для написания уравнения прямой необходимо иметь координаты направляющего вектора прямой a , или координаты нормального вектора прямой a , или угловой коэффициент прямой a .

Необходимо получить данные из заданного уравнения прямой b . По условию прямые a и b перпендикулярные, значит, направляющий вектор прямой b считается нормальным вектором прямой a . Отсюда получим, что угловые коэффициенты обозначаются как k b и k a . Они связаны при помощи соотношения k b · k a = — 1 .

Получили, что направляющий вектор прямой b имеет вид b → = ( b x , b y ) , отсюда нормальный вектор — n a → = ( A 2 , B 2 ) , где значения A 2 = b x , B 2 = b y . Тогда запишем общее уравнение прямой, проходящее через точку с координатами M 1 ( x 1 , y 1 ) , имеющее нормальный вектор n a → = ( A 2 , B 2 ) , имеющее вид A 2 · ( x — x 1 ) + B 2 · ( y — y 1 ) = 0 .

Нормальный вектор прямой b определен и имеет вид n b → = ( A 1 , B 1 ) , тогда направляющий вектор прямой a является вектором a → = ( a x , a y ) , где значения a x = A 1 , a y = B 1 . Значит осталось составить каноническое или параметрическое уравнение прямой a , проходящее через точку с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) , имеющее вид x — x 1 a x = y — y 1 a y или x = x 1 + a x · λ y = y 1 + a y · λ соответственно.

После нахождения углового коэффициента k b прямой b можно высчитать угловой коэффициент прямой a . Он будет равен — 1 k b . Отсюда следует, что можно записать уравнение прямой a , проходящей через M 1 ( x 1 , y 1 ) с угловым коэффициентом — 1 k b в виде y — y 1 = — 1 k b · ( x — x 1 ) .

Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.

Решение примеров

Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.

Записать уравнение прямой а, которая проходит через точку с координатами M 1 ( 7 , — 9 ) и перпендикулярна прямой b , которое задано каноническим уравнением прямой x — 2 3 = y + 4 1 .

Из условия имеем, что b → = ( 3 , 1 ) является направляющим вектором прямой x — 2 3 = y + 4 1 . Координаты вектора b → = 3 , 1 являются координатами нормального вектора прямой a , так как прямые a и b взаимно перпендикулярны. Значит, получаем n a → = ( 3 , 1 ) . Теперь необходимо записать уравнение прямой, проходящее через точку M 1 ( 7 , — 9 ) , имеющее нормальный вектор с координатами n a → = ( 3 , 1 ) .

Получим уравнение вида: 3 · ( x — 7 ) + 1 · ( y — ( — 9 ) ) = 0 ⇔ 3 x + y — 12 = 0

Полученное уравнение является искомым.

Ответ: 3 x + y — 12 = 0 .

Составить уравнение прямой, которая проходит через начало координат системы координат О х у z , перпендикулярно прямой 2 x — y + 1 = 0 .

Имеем, что n b → = ( 2 , — 1 ) является нормальным вектором заданной прямой. Отсюда a → = ( 2 , — 1 ) — координаты искомого направляющего вектора прямой.

Зафиксируем уравнение прямой, проходящую через начало координат с направляющим вектором a → = ( 2 , — 1 ) . Получим, что x — 0 2 = y + 0 — 1 ⇔ x 2 = y — 1 . Полученное выражение является уравнение прямой, проходящей через начало координат перпендикулярно прямой 2 x — y + 1 = 0 .

Ответ: x 2 = y — 1 .

Записать уравнение прямой, проходящей через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 .

Из уравнения y = — 5 2 x + 6 угловой коэффициент имеет значение — 5 2 . Угловой коэффициент прямой, которая перпендикулярна ей имеет значение — 1 — 5 2 = 2 5 . Отсюда делаем вывод, что прямая, проходящая через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 , равна y — ( — 3 ) = 2 5 · x — 5 ⇔ y = 2 5 x — 5 .



2.5.4. Как найти прямую, перпендикулярную данной?

В отличие от предыдущих задач п. 2.5, рассмотренные ниже схемы работают лишь в декартовой системе

координат (но не в общем аффинном случае):

Задача 79

Прямая задана уравнением  в декартовой системе координат. Составить

уравнение перпендикулярной прямой , проходящей через точку .

Решение: по условию известна точка  ( – значок принадлежности), и нам неплохо бы найти направляющий вектор прямой . Так как прямые перпендикулярны, то фокус прост:  из уравнения  «снимаем» вектор нормали: , который и будет направляющим вектором прямой .

Уравнение прямой  составим по точке  и направляющему вектору :

Ответ:

Развернём геометрический этюд:
И аналитическая проверка решения:

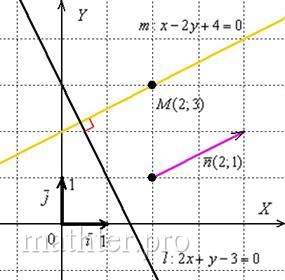
1) Из уравнений ,   вытаскиваем направляющие векторы  и с помощью скалярного произведения приходим к выводу, что прямые действительно

перпендикулярны:
.
Кстати, можно использовать векторы нормали, это даже проще.

2) Проверяем, удовлетворяет ли точка  полученному уравнению
Оба пункта легко выполнить устно!

Самостоятельно:

Задача 80

Найти точку пересечения перпендикулярных прямых , если известно уравнение  в декартовой системе координат  и точка .

В задаче несколько действий, поэтому решение удобно оформить по пунктам.

И наше увлекательное путешествие продолжается:

2.5.5. Как вычислить расстояние от точки до прямой?

2.5.3. Как найти точку пересечения прямых?

| Оглавление |



Автор: Aлeксaндр Eмeлин

Взаимосвязь между двумя линиями, пересекающимися под прямым углом (90 градусов) Отрезок AB перпендикулярен сегменту CD, поскольку два угла, которые он создает (обозначены оранжевым и синим), составляют каждый по 90 градусов. Отрезок AB можно назвать перпендикуляром от A к отрезку CD, используя слово «перпендикуляр» как существительное. Точка B называется основанием перпендикуляра от A до сегмента CD или просто основанием A на CD.

В элементарной геометрии свойство быть перпендикуляром (перпендикулярность ) — это отношение между двумя линиями , которые встречаются под прямым углом (90 градусов ). Свойство распространяется на другие связанные геометрические объекты.

Линия считается перпендикулярной другой линии, если две прямые пересекаются под прямым углом. Явно первая линия перпендикулярна второй линии, если (1) две линии встречаются; и (2) в точке пересечения прямой угол на одной стороне первой линии разрезается второй линией на два конгруэнтных угла. Можно показать, что перпендикулярность является симметричной, то есть если первая линия перпендикулярна второй линии, то вторая линия также перпендикулярна первой. По этой причине мы можем говорить о двух линиях как о перпендикулярных (друг другу) без указания порядка.

Перпендикулярность легко распространяется на сегменты и лучи. Например, отрезок линии AB ¯ { displaystyle { overline {AB}}}перпендикулярен отрезку линии CD ¯ { displaystyle { overline {CD}}}если каждая из них вытягивается в обоих направлениях, образуя бесконечную линию, эти две результирующие линии перпендикулярны в указанном выше смысле. В символах A B ¯ ⊥ C D ¯ { displaystyle { overline {AB}} perp { overline {CD}}}означает, что отрезок AB перпендикулярен отрезку линии CD. Информацию о символе перпендикуляра см. В разделе Верхний галс.

Линия считается перпендикулярной плоскости , если она перпендикулярна каждой линии в плоскости, которую она пересекает. Это определение зависит от определения перпендикулярности между линиями.

Две плоскости в пространстве называются перпендикулярными, если двугранный угол, под которым они встречаются, является прямым углом (90 градусов).

Перпендикулярность — это частный пример более общей математической концепции ортогональности ; перпендикулярность — это ортогональность классических геометрических объектов. Таким образом, в высшей математике слово «перпендикуляр» иногда используется для описания гораздо более сложных геометрических условий ортогональности, например, между поверхностью и ее нормалью.

Содержание

• 1 фут перпендикуляра
• 2 Построение перпендикуляра
• 3 Относительно параллельных прямых
• 4 При вычислении расстояний
• 5 График функций
• 6 В кругах и других конусах
  • 6.1 Окружности
  • 6.2 Эллипсы
  • 6.3 Параболы
  • 6.4 Гиперболы
• 7 В многоугольниках
  • 7.1 Треугольники
  • 7.2 Четырехугольники
• 8 Трехмерные линии
• 9 См. Также
• 10 Примечания
• 11 Ссылки
• 12 Внешние ссылки

Фунда перпендикуляра

Слово стопа часто используется в связи с перпендикулярами. Это использование проиллюстрировано на верхней диаграмме выше и в ее заголовке. Схема может быть в любой ориентации. Стопа не обязательно внизу.

Точнее, пусть A будет точкой, а m — прямой. Если B — точка пересечения m и единственной прямой, проходящей через A, которая перпендикулярна m, то B называется основанием этого перпендикуляра, проходящего через A.

Построение перпендикуляра

Построение перпендикуляра (синий) к линии AB через точку P. Построение перпендикуляра к полуоси h из точки P (применимо не только в конечной точке A, M выбирается произвольно), анимация в конце с паузой 10 с

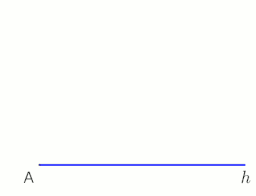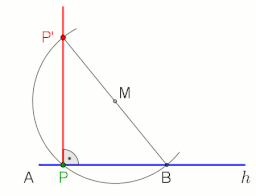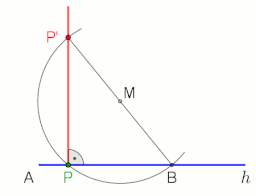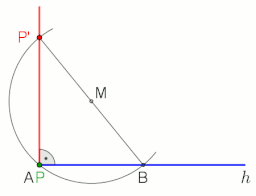
Чтобы провести перпендикуляр к линии AB через точку P с помощью построения циркуля и линейки, действуйте следующим образом (см. Рисунок слева):

• Шаг 1 (красный): постройте круг с центром в точке P для создания точек A ‘и B’ на линии AB, которые находятся на равноудалении от P.
• Шаг 2 (зеленый): построить круги с центром у A ‘и B’ равный радиус. Пусть Q и P — точки пересечения этих двух окружностей.
• Шаг 3 (синий): соедините Q и P, чтобы построить желаемый перпендикуляр PQ.

Чтобы доказать, что PQ перпендикулярен AB, используйте теорему сравнения SSS для ‘и QPB’, чтобы сделать вывод, что углы OPA ‘и OPB’ равны. Затем используйте теорему сравнения SAS для треугольников OPA ‘и OPB’, чтобы сделать вывод, что углы POA и POB равны.

Чтобы провести перпендикуляр к линии g в точке P или через нее, используя теорему Фалеса, см. Анимацию справа.

Теорема Пифагора может быть использована как основа методов построения прямых углов. Например, посчитав звенья, можно сделать три отрезка цепи с длинами в соотношении 3: 4: 5. Их можно выложить в виде треугольника, у которого будет прямой угол напротив его самой длинной стороны. Этот метод полезен для разбивки садов и полей, где размеры велики и не требуется большой точности. Цепи можно использовать повторно, когда это необходимо.

По отношению к параллельным линиям

Знаки стрелок указывают на то, что линии a и b, отрезанные поперечной линией c, параллельны.

Если две прямые (a и б) оба перпендикулярны третьей линии (в), все углы, образованные вдоль третьей линии, являются прямыми углами. Следовательно, в евклидовой геометрии любые две прямые, которые обе перпендикулярны третьей линии, параллельны друг другу из-за постулата параллельности. И наоборот, если одна линия перпендикулярна второй линии, она также перпендикулярна любой линии, параллельной этой второй линии.

На рисунке справа все углы, заштрихованные оранжевым, конгруэнтны друг другу, а все углы, заштрихованные зеленым, конгруэнтны друг другу, поскольку вертикальные углы совпадают и чередующиеся внутренние углы, образованные поперечными параллельными линиями разреза, совпадают. Следовательно, если прямые a и b параллельны, любой из следующих выводов приводит ко всем остальным:

• Один из углов на диаграмме — прямой угол.
• Один из углов, заштрихованных оранжевым. конгруэнтна одному из углов, закрашенных зеленым.
• Линия c перпендикулярна линии a.
• Линия c перпендикулярна линии b.

При вычислении расстояний

Расстояние от точки до линии — это расстояние до ближайшей точки на этой линии. Это точка, в которой отрезок от нее до данной точки перпендикулярен прямой.

Аналогично, расстояние от точки до кривой измеряется отрезком линии, перпендикулярным касательной линии к кривой в ближайшей точке на кривая.

Перпендикулярная регрессия подгоняет линию к точкам данных за счет минимизации суммы квадратов перпендикулярных расстояний от точек данных до линии.

Расстояние от точки до плоскости измеряется как длина от точки вдоль сегмента, перпендикулярного плоскости, то есть перпендикулярно всем линиям в плоскости, которые пройти через ближайшую точку на плоскости к данной точке.

График функций

В двумерной плоскости прямые углы могут быть образованы двумя пересекающимися линиями, если произведение их наклонов равно −1. Таким образом, определяя две линейные функции : y 1 = a 1 x + b 1 и y 2 = a 2 x + b 2, графики функций будут перпендикулярны и образуют четыре прямых угла в местах пересечения линий, если a 1a2= −1. Однако этот метод нельзя использовать, если наклон равен нулю или не определен (линия параллельна оси).

Для другого метода пусть две линейные функции имеют вид: a 1 x + b 1 y + c 1 = 0 и a 2 x + b 2 y + c 2 = 0. Линии будут перпендикулярными тогда и только тогда, когда a 1a2+ b 1b2= 0. Этот метод упрощен из скалярного произведения (или, в более общем смысле, внутреннего произведения ) векторов . В частности, два вектора считаются ортогональными, если их внутренний продукт равен нулю.

В кругах и других кониках

Окружности

Каждый диаметр круга окружности перпендикулярен касательной . к этой окружности в точке, где диаметр пересекает окружность.

Отрезок, проходящий через центр окружности пополам хорду, перпендикулярен хорде.

Если пересечение любых двух перпендикулярных хорд делит одну хорду на длины a и b и делит другую хорду на длины c и d, то a + b + c + d равно квадрату диаметра.

Сумма квадратов длин любых двух перпендикулярных хорд, пересекающихся в данной точке, такая же, как и у любых других двух перпендикулярных хорд, пересекающихся в той же точке, и задается формулой 8r — 4p (где r — длина окружности радиус, а p — расстояние от центральной точки до точки пересечения).

Теорема Фалеса утверждает, что две прямые, проходящие через одну и ту же точку на окружности, но проходящие через противоположные конечные точки диаметра, перпендикулярны. Это эквивалентно тому, что любой диаметр окружности образует прямой угол в любой точке окружности, кроме двух конечных точек диаметра.

Эллипсы

Большая и малая оси эллипса перпендикулярны друг другу и касательным линиям к эллипсу в точках, где оси пересекают эллипс.

Большая ось эллипса перпендикулярна направляющей и каждой прямой кишке.

Параболе

в параболе ось симметрии перпендикулярна прямой кишке, директрисе и касательной в точке, где ось пересекает параболу.

От точки на касательной к вершине параболы другая касательная линия к параболе перпендикулярна прямой, идущей от этой точки через фокус параболы.

ортоптическое свойство параболы заключается в том, что если две касательные к параболе перпендикулярны друг другу, то они пересекаются по направляющей. И наоборот, две касательные, пересекающиеся на директрисе, перпендикулярны. Это означает, что если смотреть из любой точки на своей директрисе, любая парабола имеет прямой угол.

Гиперболы

Поперечная ось гиперболы перпендикулярна сопряженной оси и каждой направляющей.

Произведение перпендикулярных расстояний от точки P на гиперболе или на ее сопряженной гиперболе до асимптот является константой, не зависящей от местоположения P.

A прямоугольная гипербола имеет асимптоты, которые перпендикулярны друг другу. Его эксцентриситет равен 2. { displaystyle { sqrt {2}}.}

В многоугольниках

Треугольники

Катеты прямоугольного треугольника перпендикулярны друг другу.

высоты треугольника перпендикулярны их соответствующим основаниям. серединные перпендикуляры сторон также играют важную роль в геометрии треугольника.

Линия Эйлера равнобедренного треугольника перпендикулярна основанию треугольника.

Теорема о прямой линии Дроза-Фарни касается свойства двух перпендикулярных прямых, пересекающихся в ортоцентре.

треугольника.

Теорема Харкурта касается отношения отрезков прямой через вершина и перпендикулярна любой прямой касательной к треугольнику , вписанной в круг.

Четырехугольники

в квадрате или другом прямоугольнике , все пары смежных сторон перпендикулярны. Правая трапеция — это трапеция , имеющая две пары смежных сторон, перпендикулярных.

Каждая из четырех солодов четырехугольника является перпендикуляром к стороне, проходящей через среднюю точку противоположной стороны.

Ортодиагональный четырехугольник — это четырехугольник, диагонали перпендикулярны. К ним относятся квадрат, ромб и воздушный змей. Согласно теореме Брахмагупты в ортодиагональном четырехугольнике, который также является циклическим, линия, проходящая через середину одной стороны и точку пересечения диагоналей, перпендикулярна противоположной стороне.

Согласно теореме ван Обеля, если квадраты построены снаружи по сторонам четырехугольника, отрезки прямых, соединяющие центры противоположных квадратов, перпендикулярны и равны по длине.

Линии в трех измерениях

До трех линий в трехмерном пространстве могут быть попарно перпендикулярны, например, оси x, y и z трех -мерная декартова система координат.

См. также

Примечания

Ссылки

• Альтшиллер-Корт, Натан (1925), Геометрия колледжа: Введение в Современная геометрия треугольника и круга (2-е изд.), Нью-Йорк: Barnes Noble, LCCN 52-13504
• Кей, Дэвид К. (1969)), College Geometry, Нью-Йорк: Холт, Райнхарт и Уинстон, LCCN 69-12075

Внешние ссылки

Как составить уравнение прямой перпендикулярной данной прямой и проходящей через данную точку?

Пусть y=k₁x+b₁ — данная прямая. С учётом условия перпендикулярности прямых уравнение прямой, перпендикулярной данной, имеет вид

   

Если эта прямая проходит через точку M(x_o; y_o), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение x_o и y_o, мы найдем b.

Примеры.

1) Написать уравнение прямой, проходящей через точку A(-10;3), перпендикулярной прямой y=5x-11.

Решение:

Так как прямые перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, то

   

Значит уравнение прямой, перпендикулярной прямой y=5x-11, имеет вид

   

Так как прямая проходит через точку A(-10;3), то координаты A удовлетворяют уравнению прямой:

   

откуда b=1.

Итак, уравнение прямой, перпендикулярной прямой y=5x-11 и проходящей через точку A(-10;3)

   

Ответ: y= -0,2x+1.

2) Написать уравнение прямой, перпендикулярной прямой x= -2, проходящей через точку M(-5;9).

Решение:

Прямая x= -2 перпендикулярна оси абсцисс. Значит, прямая, уравнение которой мы ищем, параллельна оси абсцисс, то есть ищем уравнение прямой в виде y=b.

Так как искомая прямая проходит через точку M(-5;9), то координаты M удовлетворяют уравнению прямой: y=9.

Ответ: y=9.

3) Написать уравнение прямой, перпендикулярной прямой y=4, проходящей через точку F(7;-5).

Решение:

Прямая y=4 перпендикулярна оси ординат. Следовательно, прямая, уравнение которой мы ищем, параллельна оси ординат, а значит, её уравнение имеет вид x=a.

Так как эта прямая проходит через точку F(7;-5), то координаты F удовлетворяют уравнению прямой: x=7.

Ответ: x=7.