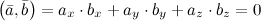Содержание:
- Формула
- Примеры нахождения перпендикулярного вектора
Формула
Для того чтобы вектор $bar{a}$ был перпендикулярен вектору
$bar{b}$ необходимо, чтобы их
скалярное произведение было равно нулю, то есть
В случае если векторы заданы на плоскости своими координатами
$bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, то условие их перпендикулярности примет вид:
$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}=0$$
Если векторы заданны в пространстве и имеют координаты
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то условие перпендикулярности запишется в виде:
$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}=0$$
Примеры нахождения перпендикулярного вектора
Пример
Задание. Даны два вектора
$bar{a}=(2 ;-1)$ и $bar{b}=(-3 ; m)$ . При каком значении
$m$ эти векторы будут перпендикулярны?
Решение. Для того чтобы векторы
$bar{a}$ и
$bar{b}$ были перпендикулярны необходимо, чтобы их скалярное
произведение было равно нулю, то есть выполнялось условие:
$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}=0$$
Подставим в это выражение координаты заданных векторов и из полученного равенства найдем
$m$:
$$2 cdot(-3)+(-1) cdot m=0$$
$$-6-m=0$$
$$m=-6$$
Ответ. Векторы
$bar{a}$ и
$bar{b}$ будут перпендикулярны при $m=-6$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Заданы два вектора
$bar{a}=(3 ;-2 ; m)$ и $bar{b}=(-1 ; m ; 1)$ . При каком значении
$m$ эти векторы будут перпендикулярны?
Решение. Два вектора
$bar{a}$ и
$bar{b}$ будут перпендикулярны тогда, когда их скалярное
произведение будет равняться нулю. И так как векторы заданны в пространстве, то должно выполнялось условие:
Подставим в него заданные координаты векторов, получим:
$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}=0$$
$$3 cdot(-1)+(-2) cdot m+m cdot 1=0$$
$$3-2 cdot m+m=0$$
Из полученного уравнения найдем $m$:
$$3-m=0 Rightarrow m=-3$$
Ответ. Векторы
$bar{a}$ и
$bar{b}$ будут перпендикулярны при
$m=-3$
Читать дальше: как найти орт вектора.
© 2011-2023 Довжик Михаил
Копирование материалов запрещено.
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com
Анна Кирпиченкова
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Понятие вектора и перпендикулярности векторов
Вначале надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.
Определение 1
Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.
Определение 2
Концами отрезка будем называть точки, которые его ограничивают.
Для введения определения вектора один из концов отрезка назовем его началом.
Определение 3
Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.
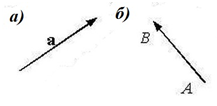
Обозначение: $overline{AB}$ — вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.
Иначе одной маленькой буквой: $overline{a}$ (рис. 1).
Определение 4
Нулевым вектором будем называть любую точку, которая принадлежит плоскости.
Обозначение: $overline{0}$.
Введем теперь, непосредственно, определение коллинеарных векторов.
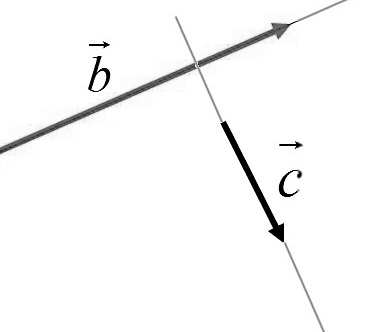
Определение 5
Два ненулевых вектора будем называть перпендикулярными (ортогональными), если они лежат на каких-либо перпендикулярных прямых (рис.2).
«Как найти вектор, перпендикулярный вектору» 👇
Также введем определение скалярного произведения, которое будет нам необходимо далее.
Определение 6
Скалярным произведением двух данных векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.
Математически это может выглядеть следующим образом:
$overline{α}overline{β}=|overline{α}||overline{β}|cos∠(overline{α},overline{β})$
Скалярное произведение также можно найти с помощью координат векторов следующим образом
$overline{α}overline{β}=α_1 β_1+α_2 β_2+α_3 β_3$
Признак перпендикулярности через пропорциональность
Теорема 1
Чтобы ненулевые векторы были перпендикулярны между собой, необходимо и достаточно, чтобы их скалярное произведение этих векторов равнялось нулю.
Доказательство.
Необходимость: Пусть нам даны векторы $overline{α}$ и $overline{β}$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они перпендикулярны друг другу. Тогда нам нужно доказать следующее равенство
$overline{α}cdot overline{β}=0$
Так как векторы $overline{α}$ и $overline{β}$ перпендикулярны, то угол между ними равняется $90^0$. Найдем скалярное произведение данных векторов по формуле из определения 6.
$overline{α}cdot overline{β}=|overline{α}||overline{β}|cos90^circ =|overline{α}||overline{β}|cdot 0=0$
Достаточность: Пусть верно равенство $overline{α}cdot overline{β}=0$. Докажем, что векторы $overline{α}$ и $overline{β}$ будут перпендикулярны друг другу.
По определению 6, будет верно равенство
$|overline{α}||overline{β}|cos∠(overline{α},overline{β})=0$
$cos∠(overline{α},overline{β})=0$
$∠(overline{α},overline{β})=90^circ$
Следовательно, векторы $overline{α}$ и $overline{β}$ будут перпендикулярны друг другу.
Теорема доказана.
Пример 1
Доказать, что векторы с координатами $(1,-5,2)$ и $(2,1,3/2)$ перпендикулярны.
Доказательство.
Найдем скалярное произведение для этих векторов через формулу, данную выше
$overline{α}cdot overline{β}=1cdot 2+(-5)cdot 1+2cdot frac{3}{2}=2cdot 5+3=0$
Значит, по теореме 1, эти вектор перпендикулярны.
Нахождение перпендикулярного вектора к двум данным векторам через векторное произведение
Введем вначале понятие векторного произведения.
Определение 7
Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.
Обозначение: $overline{α}хoverline{β}$.
Чтобы найти векторное произведение, будем пользоваться формулой
$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}$
Так как вектор векторного произведения двух векторов перпендикулярен обоим этим векторам, то он и будет иском вектором. То есть, для того, чтоб найти перпендикулярный для двух векторов вектор, нужно просто найти их векторное произведение.
Пример 2
Найти вектор, перпендикулярный к векторам с координатами $overline{α}=(1,2,3)$ и $overline{β}=(-1,0,3)$
Решение.
Найдем векторное произведение данных векторов.
$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\1&2&3\-1&0&3end{vmatrix}=(6-0)overline{i}-(3+3)overline{j}+(0+2)overline{k}=6overline{i}-6overline{j}+2overline{k}=(6,6,2)$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Онлайн калькулятор для решения задач и работы с векторами. Зная точки вектора или координаты начала и конца вектора, векторный калькулятор использует данные по всем разделам векторов и находит не только координаты самого вектора, его направляющие косинусы и результаты сложения, вычитания и умножения, но и доказывает ортогональность или коллинеарность двух векторов, а также
угол между векторами, длину или модуль векторов, проекцию векторов, векторное произведение векторов, площадь параллелограмма и площадь треугольника построенного на векторах. Для отображение деталей расчетов активируйте формулы на панели калькулятора.
| AC | 7 | 8 | 9 | ← |
| C | 4 | 5 | 6 | ÷ |
| % | 1 | 2 | 3 | × |
| xy | . | 0 | = | — |
| x2 | √ | ( | ) | + |
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Длина (модуль) вектора
Длина вектора на плоскости
Формула длины (модуля) вектора на плоскости вычисляется по формуле:
$$
a⃗ = sqrt{x^2 + y^2}
$$
Длина вектора в пространстве
Формула длины (модуля) вектора в пространстве вычисляется по формуле:
$$
a⃗ = sqrt{x^2 + y^2 + z^2}
$$
Скалярное произведение векторов
Cкалярное произведение векторов
Скалярное произведение векторов на плоскости вычисляется по формуле:
$$
a⃗ * b⃗ = A_X * B_X + A_Y * B_Y
$$
Скалярное произведение векторов через координаты точек вектора
Скалярное произведение векторов заданных через уравнение
Первое уравнение имеет вид:
$$
q⃗ = A * a⃗ + B * b⃗
$$
Второе уравнение имеет вид:
$$
p⃗ = C * a⃗ + D * b⃗
$$
Где A,B,C,D
– коэффициенты перед векторами
– длина (модуль) вектора
Векторное произведение векторов
Смешанное произведение векторов
Смешанным произведением трех векторов a, b, c называется число равное векторному произведению a x b, умноженному скалярно на вектор c.
Взаимное расположение двух векторов
Данный калькулятор определяет, являются ли заданные вектора коллинеарными или перпендикулярными.
Вектора перпендикулярны, если скалярное произведение равно нулю
Вектора параллельны (коллинеарные), если координаты векторов пропорциональны, т.е.
$$
X_1 = λ * X_2 : Y_1 = λ * Y_2 : Z_1 = λ * Z_2
$$
Расположение векторов на плоскости
Расположение векторов в пространстве
Угол между векторами
Угол между векторами на плоскости
Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.
$$
cos(α) = {a⃗ * b⃗ over |a| * |b|}
$$
Угол между векторами в пространстве
Середина отрезка
Введите координаты точек.
Координаты середины отрезка с концами A(x1,y1) и B(x2,y2) вычисляются по формалуе
{
$$
X = {X_1 + X_2 over 2}
$$
$$
Y = {Y_1 + Y_2 over 2}
$$
Введите координаты точек в пространстве
Сложение и вычитание векторов
Формулы сложения и вычитания векторов
$$
a⃗ + b⃗ = {A_X + B_X : A_Y + B_Y}
$$
$$
a⃗ — b⃗ = {A_X — B_X : A_Y — B_Y}
$$
Проекция вектора на ось
Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b.
$$
b⃗_{a⃗} = {a⃗ * b⃗ over |b|}
$$