Как найти перпендикуляры ромба

В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – ромба.

Определение ромба

Ромб – это фигура на плоскости; разновидность параллелограмма, у которого все четыре стороны равны и попарно параллельны. Обычно ромб обозначается названиями его вершин (например, ABCD), а длина его стороны – строчной латинской буквой (например, a).

• AB = BC = CD = AD = a
• AB параллельна CD, BC параллельна AD.

Примечание: квадрат является частным случаем ромба.

Свойства ромба

Свойство 1

Противоположные углы ромба равны между собой, а сумма соседних углов составляет 180°.

• ∠ABC = ∠ADC, ∠BAD = ∠BCD
• α + β = 180°

Свойство 2

Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.

• диагональ BD (d₁) перпендикулярна диагонали AC (d₂)
• AE = EC
• BE = ED

В результате пересечения диагоналей ромб делится на 4 прямоугольных треугольника: ΔAEB, ΔBEC, ΔAED и ΔDEC.

Свойство 3

Диагонали ромба являются биссектрисами его углов.

Свойство 4

Сторону ромба a можно найти через его диагонали d₁ и d₂ (согласно теореме Пифагора).

• a – гипотенуза любого из 4 прямоугольных треугольников (например, ΔBEC);
• половины диагоналей d₁ и d₂ – катеты треугольников.

Свойство 5

В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

Радиус вписанной в ромб окружности r вычисляется по формуле:

Признаки ромба

Параллелограмм является ромбом только в том случае, если для него верно одно из следующих утверждений:

1. Его диагонали пересекаются под прямым углом.
2. Если его диагонали являются биссектрисами его углов.
3. Две смежные стороны равны (следовательно, все стороны равны).

Примечание: Любой четырехугольник, стороны которого равны, является ромбом.

Определение

Ромб – это параллелограмм, у которого все стороны равны.

Таким образом, ромб обладает всеми свойствами параллелограмма:

(sim) противоположные углы ромба попарно равны;

(sim) соседние углы ромба в сумме дают (180^circ);

(sim) диагонали точкой пересечения делятся пополам.

Теорема: свойство ромба

Диагонали ромба перпендикулярны и делят его углы пополам.

Доказательство

По определению ромба (AB = AD), поэтому треугольник (BAD) равнобедренный. Так как ромб – параллелограмм, то его диагонали точкой (O) пересечения делятся пополам. Следовательно, (AO) – медиана равнобедренного треугольника (BAD), а значит, высота и биссектриса этого треугольника. Поэтому (ACperp BD) и (angle BAC =
angle DAC).

Теорема: признаки ромба

1. Если в параллелограмме диагонали перпендикулярны, то это – ромб.

2. Если в параллелограмме диагонали делят его углы пополам, то это – ромб.

3. Если в выпуклом четырехугольнике все стороны равны, то он – ромб.

Доказательство

1) Рассмотрим параллелограмм (ABCD). Пусть (ACperp BD).

Т.к. в параллелограмме диагонали точкой пересечения делятся пополам, то в треугольнике (ABD) отрезок (AO) – медиана. Т.к. к тому же (AO) – высота (следует из условия), то (triangle ABD) – равнобедренный, т.е. (AB=AD). Т.к. у параллелограмма противоположные стороны равны, то отсюда следует, что все его стороны будут равны.

2) Пусть (AC) – биссектриса угла (angle A).

Т.к. в параллелограмме диагонали точкой пересечения делятся пополам, то в треугольнике (ABD) отрезок (AO) – медиана. Т.к. к тому же (AO) – биссектриса (следует из условия), то (triangle ABD) – равнобедренный, т.е. (AB=AD). Т.к. у параллелограмма противоположные стороны равны, то отсюда следует, что все его стороны будут равны.

3) Пусть (ABCD) – произвольный четырехугольник и (AB=BC=CD=AD).

Т.к. противоположные стороны четырехугольника попарно равны, то он – параллелограмм. Т.к. у него все стороны равны, то по определению это ромб.

Что Вы подразумеваете под «перпендикулярами ромба»?

Проекция точки S на плоскость ромба попадает на пересечение его диагоналей (точку О).

По теореме Пифагора легко вычисляем, что сторона ромба равна 25 см. Площадь ромба равна половине произведения его диагоналей, т.е. S=30*40/2=600 см^2. С другой стороны, она равна произведению стороны ромба на его высоту. Значит высота ромба (расстояние между противоположными сторонами) равна 600/25=24 см. Расстояние от центра ромба до любой его стороны равно 24/2=12 см. Опустим из точки S перпендикуляр к любой его стороне. Он равен 20 см, а его проекция на плоскость ромба — равна 12 см. Тогда расстояние от точки S до плоскости ромба (по теореме Пифагора) равно 16 см. Видимо это расстояние и нужно определить.

Ромб,
его свойства и признаки.

     Рассмотрим ещё два вида
параллелограмма.

Определение. Ромбом
называется параллелограмм, у которого все стороны равны.

                       

Поскольку ромб
является параллелограммом, то он обладает теми же свойствами, что и
параллелограмм, т.е.: у ромба противолежащие углы равны (стороны у него и так
все равны, поэтому в этом свойстве мы опускаем равенство противолежащих сторон);
диагонали ромба пересекаются и точкой пересечения делятся пополам. Кроме того,
ромб обладает ещё и своими, особенными свойствами. Рассмотрим их.

ТЕОРЕМА. 
У ромба диагонали взаимно перпендикулярны.

                           
Дано:  – ромб

                                       
 и  диагонали.

                   
Доказать: .

Доказательство.

Для того, чтобы доказать, что , нам нужно доказать, что
хотя бы один из четырёх углов, которые получаются при пересечении диагоналей,
равен .

1. Рассмотрим  и .

   по III
признаку равенства треугольников. Следовательно, все соответствующие углы  у
этих треугольников равны, т.е. .

2.  и  – смежные, значит, по
свойству смежных углов

, как, впрочем, и остальные
углы (мы знаем, что если угол  прямой, то смежный с ним угол также прямой).

3. Итак, прямые  и  при пересечении образуют
прямой угол, значит, эти прямые перпендикулярны, т.е. , ч.т.д.

ТЕОРЕМА.  У ромба диагонали
являются биссектрисами углов.

                      

                           
Дано:  – ромб

                                       
 и  диагонали.

                   
Доказать:  – биссектриса  и

                                      
 – биссектриса
 и .

Доказательство.

Для того, чтобы доказать, что  и  являются биссектрисами
углов, нам нужно доказать, что они делят эти углы пополам.

1. Рассмотрим  и .

   по III
признаку равенства треугольников. Следовательно, все соответствующие углы  у
этих треугольников равны, т.е.  и . Следовательно,  – биссектриса
 и .

2. Рассмотрим
 и .

   по III
признаку равенства треугольников. Следовательно, все соответствующие углы  у
этих треугольников равны, т.е.  и . Следовательно,  – биссектриса  и ,  ч.т.д.

ТЕОРЕМА.  У ромба высоты равны.

                           
Дано:  – ромб

                                       
 и  — высоты.

                   
Доказать:

Доказательство.

Рассмотрим
 и .

 по признаку равенства
прямоугольных треугольников (по гипотенузе и острому углу). Значит, все
соответствующие стороны у этих треугольников равны, т.е. , ч.т.д.

Итак, ромб обладает следующими свойствами:

1.      У
ромба диагонали пересекаются и точкой пересечения делятся пополам.

2.      У
ромба диагонали взаимно перпендикулярны.

3.      У
ромба диагонали являются биссектрисами его углов.

4.      У
ромба противоположные углы равны.

5.      У
ромба высоты равны.

Теперь определим признаки ромба.

ТЕОРЕМА (I
признак ромба).  Если у параллелограмма две
смежные стороны равны, то такой параллелограмм является ромбом.

                        
   Дано:  – параллелограмм

  
                                    

                   
Доказать:  – ромб.

Доказательство.

    
Так как  – параллелограмм, то у него
противолежащие стороны равны.

 – ромб (по определению),
ч.т.д.

ТЕОРЕМА (II
признак ромба). Если у параллелограмма диагонали
взаимно перпендикулярны, то такой параллелограмм является ромбом.

                        
   Дано:  – параллелограмм

  
                                    

                   
Доказать:  – ромб.

Доказательство.

Рассмотрим
.

 по свойству диагоналей
параллелограмма, значит,  – медиана (по опред-нию).

 – высота , т.к. . Значит, в     является и медианой и
высотой, поэтому этот треугольник является равнобедренным (по признаку
равнобедренного треугольника), т.е. . Согласно I
признаку ромба, параллелограмм  является ромбом, ч.т.д.

ТЕОРЕМА (III
признак ромба). Если у параллелограмма диагональ
является биссектрисой его угла, то этот параллелограмм является ромбом.

                        
   Дано:  – параллелограмм

  
                                     – диагональ

                           
            – биссектриса

                   
Доказать:  – ромб.

Доказательство.

Так как  – биссектриса , то .

 по свойству внутренних
накрест лежащих углов при параллельных прямых. Значит, , следовательно  – равнобедренный, и . По I
признаку ромба, параллелограмм  является ромбом, ч.т.д.

ТЕОРЕМА (IV
признак ромба). Если у параллелограмма высоты
равны, то такой параллелограмм является ромбом.

                        
   Дано:  – параллелограмм

  
                                     и  — высоты

                           
           

                   
Доказать:  – ромб.

Доказательство.

Рассмотрим
 и .

 по признаку равенства
прямоугольных треугольников (по катету и острому углу). Значит, все
соответствующие стороны у этих треугольников равны, т.е. . По I
признаку ромба, параллелограмм  является ромбом, ч.т.д.

ТЕОРЕМА (V
признак ромба). Если в четырёхугольнике все
стороны равны, то он является ромбом.

                        
   Дано:  – четырёхугольник

  
                                    

                   
Доказать:  – ромб.

Доказательство.

Проведём диагональ  и рассмотрим  и .

 по III признаку равенства треугольников, следовательно, все соответствующие
углы у этих треугольников равны, т.е.  и . Значит, по признаку
параллельности прямых,  и , следовательно,  – параллелограмм, у которого
все стороны равны, значит, он является ромбом, ч.т.д.

Итак, признаки ромба:

1.      Если
у параллелограмма две смежные стороны равны, то такой параллелограмм является
ромбом.

2.      Если
у параллелограмма диагонали взаимно перпендикулярны, то такой параллелограмм
является ромбом.

3.      Если
у параллелограмма диагональ является биссектрисой его угла, то этот
параллелограмм является ромбом.

4.      Если
у параллелограмма высоты равны, то такой параллелограмм является ромбом.

5.      Если
в четырёхугольнике все стороны равны, то он является ромбом.

1.   Сторона
ромба равна  см. Найдите периметр ромба.

2.   Вычислите
периметр ромба, один из углов которого равен , а длина меньшей диагонали
равна  см.

3.      Найдите
все углы ромба, если его сторона равна диагонали.

4.   Диагонали
ромба  пересекаются в точке . Найдите углы треугольника , если .

5.   Из
вершины  ромба  проведены перпендикуляры  и  к прямым  и . Докажите, что луч  является биссектрисой .

6.   Сторона
ромба  равна  см, . Из вершины  проведены высоты  и  к сторонам  и  соответственно. Найдите
расстояния . Докажите, что треугольник  равносторонний.

7.      Найдите
углы ромба, если основание перпендикуляра, опущенного из вершины тупого угла,
делит сторону ромба пополам.

8.   Периметр
ромба равен  см, расстояние между
противолежащими сторонами равно  см. Найдите углы ромба.

9.      Найдите
углы, которые образуют диагонали ромба с его сторонами, если один из углов
ромба равен .

10.  Найдите
углы ромба, если его диагонали составляют с его стороной углы, один из которых
на  меньше другого.

11. Углы,
образуемые стороной ромба с его диагоналями, относятся как . Найдите углы ромба.

12.  Докажите,
что точка пересечения диагоналей ромба равноудалена от его сторон.

13.  Докажите,
что параллелограмм, у которого две смежные стороны равны, является ромбом.

14.  Докажите,
что если каждая диагональ четырёхугольника делит пополам два его угла, то этот
четырёхугольник является ромбом.

15.  Через
точку пересечения диагоналей ромба проведены перпендикуляры к его сторонам.
Докажите, что точки пересечения этих перпендикуляров со сторонами ромба
являются вершинами прямоугольника.

16.  Точки  – середины сторон ромба . Докажите, что
четырёхугольник  является
прямоугольником.

17. В
ромбе  точки   – середины его сторон.
Докажите, что точки   лежат на одной прямой с
серединами отрезков: а)  и   б)  и .

18. В
параллелограмме  биссектрисы углов  и  пересекают стороны
параллелограмма  и  в точках  и  соответственно. Докажите, что
четырёхугольник  – ромб.

19. В
ромбе  биссектриса угла  пересекает сторону  и диагональ  соответственно в точках  и . Найдите угол , если .

20.

В ромбе  угол  равен . Докажите, что если один из
углов треугольника  равен , то и остальные его углы тоже
равны по .

21. Расстояние
от точки пересечения диагоналей ромба  до прямой  равно  м. Найдите длину высоты
ромба, проведённой к стороне .

22.  В
ромбе перпендикуляр, проведённый из вершины тупого угла к стороне ромба, делит
эту сторону пополам. Найдите углы ромба.

23.  Докажите,
что четырёхугольник, вершины которого находятся в серединах сторон
прямоугольника, является ромбом.

24. Периметр
ромба  равен  см. Найдите сторону ромба.

25. В
ромбе  с острым углом , равным , проведена диагональ . Найдите угол .

26. В
ромбе  с тупым углом  диагонали пересекаются в
точке . Один из углов треугольника  равен . Найдите остальные углы этого
треугольника и угол .

27. В
ромбе . Диагонали пересекаются в
точке . Найдите углы треугольника .

28. В
ромбе  – точка пересечения
диагоналей,  – перпендикуляры, опущенные
на стороны  соответственно. Докажите, что
, и найдите сумму углов  и .

29. В
ромбе  диагонали пересекаются в
точке . На сторонах  взяты точки  соответственно, . Докажите, что , и найдите сумму углов  и .

30. В
ромбе  угол  тупой. На стороне  взята точка . Прямые  и  пересекаются в точке . Найдите угол .

31. В
ромбе  угол  острый. Отрезок  является перпендикуляром к
прямой  – точка пересечения
диагоналей, а  – общая точка прямых  и . Найдите .

32.  Два
ромба имеют общую точку пересечения диагоналей, причём, меньшие диагонали этих
ромбов взаимно перпендикулярны. Докажите, что прямая, проходящая через точку
пересечения диагоналей и середину стороны одного ромба, перпендикулярна стороне
другого.

33. Два
ромба  и  имеют общую вершину острого
угла, причём, , а лучи  и  пересекаются в точке  – точка пересечения
диагоналей ромба  – биссектриса треугольника . Докажите, что .

34. На
сторонах  ромба  взяты точки  соответственно. Каждая из
прямых  параллельная одной из осей
симметрии ромба. Диагональ  пересекает отрезок  в точке , о отрезок  – в точке . Докажите, что диагонали
четырёхугольника  равны, и определите вид
выпуклого четырёхугольника .

35.  Найдите
величину большего угла ромба, если его сторона равна одной из его диагоналей.

36.

Точка  лежит на стороне  параллелограмма  так, что  – биссектриса угла . Прямая  параллельна  и пересекает сторону  в точке . Найдите величину угла между
прямыми  и .

37. Отрезки
 – биссектрисы углов
параллелограмма . Отрезки  и  пересекаются в точке , а отрезки  и  – в точке , при этом . Найдите длину отрезка .

38.

В ромбе  диагонали  и  пересекаются в точке . Найдите углы треугольника .

39. Диагонали
 и  ромба  пересекаются в точке . Найдите углы треугольника .

40. Диагонали
ромба  пересекаются в точке . Найдите углы треугольника , если .

41. На
стороне  параллелограмма  взята точка  так, что .

а) Докажите, что  – биссектриса угла .

б) Найдите периметр
параллелограмма, если .

42. В
параллелограмме  проведена биссектриса угла , которая пересекает сторону  в точке .

а) Докажите, что
треугольник  равнобедренный.

б) Найдите сторону , если , а периметр параллелограмма
равен .

43. Один
из углов ромба равен . Определите остальные углы.

44. В
ромбе  проведена диагональ . Определите вид треугольника  и найдите его углы, если .

45. В
ромбе , диагонали пересекаются в
точке . Найдите углы треугольника .

46.

Определите вид четырёхугольника  и найдите его периметр, если .

47. Диагонали
ромба  пересекаются в точке . Найдите углы  и , если .

48. Известно,
что четырёхугольник  является ромбом. Докажите,
что .

49. Один
из углов ромба  на  больше другого. Найдите углы
треугольника , если  – точка пересечения
диагоналей.

50. На
рисунке   – равнобедренный, точки   и  – середины его боковых
сторон,  – точка на основании,  . Определите вид
четырёхугольника  и найдите его периметр, если  см.

51.

В ромбе . Найдите углы треугольника .

52. Сторона
ромба образует с его диагоналями углы, разность которых равна . Определите углы ромба.

53. Углы,
образуемые стороной ромба с его диагоналями, относятся как . Определите углы ромба.

54. Углы,
образуемые стороной ромба с его диагоналями, относятся как . Определите углы ромба.

55. Найдите
острый угол ромба , если высота , проведённая из вершины
тупого угла, делит сторону  пополам.

56. На
каждой стороне ромба  отложены, как показано на
рисунке, равные отрезки . Определите вид
четырёхугольника . Ответ объясните.

57.

В ромбе  из вершины тупого угла  проведена высота  к стороне , а из вершины тупого угла  проведена высота  к стороне . Определите взаимное
расположение прямых  и .

58.

В равнобедренный треугольник  вписан ромб , имеющий с ним общий угол.
Найдите периметр ромба, если боковая сторона треугольника равна  см.

59. В
ромбе  биссектриса угла  делит сторону ромба пополам.
Найдите тупой угол ромба.

60. Один
из углов ромба  равен . Найдите угол между меньшей
диагональю ромба и его стороной.

61. В
ромбе  диагонали пересекаются в
точке . Найдите углы ромба, если
разность  и  равна .

62. В
ромбе  диагонали пересекаются в
точке . Найдите углы ромба, если .

63. Периметр
ромба равен , один из его углов . Найдите меньшую диагональ
ромба.

64. Сторона
ромба равна  см, а острый угол равен . Из вершины тупого угла
проведена высота, которая делит сторону на два отрезка. Найдите длины этих
отрезков.

65. Диагональ
ромба, лежащая напротив угла , равна . Найдите периметр ромба.

Ромб

Определение ромба

Определение 1. Ромб − это параллелограмм, у которого все стороны равны.

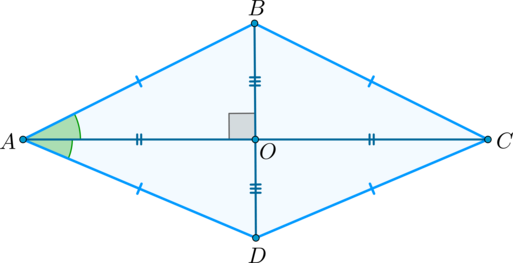
На рисунке 1 изображен ромб ABCD.

Определение 2. Ромб − это четырехугольник, у которого все стороны равны.

Ромб разделяет плоскость на две части, одна из которых называется внутренней областью ромба, а другая внешней областью ромба.

Объединение ромба и ограниченной им части плоскости также называют ромбом.

Свойства ромба

Поскольку ромб является параллелограммом, то имеет следующие свойства:

• 1. У ромба противолежащие углы равны (( small angle A = angle C, ; angle B = angle D.) )
• 2. У ромба противолежащие стороны равны (( small AB = DC, ; BC=AD.) )
• 3. У ромба противолежащие стороны параллельны ( small( AB || DC, ; BC || AD).)
• 4. У ромба соседние углы дополняют друг друга до 180° ( small ( angle A +angle B=180°, ) ( small angle C + angle D=180°).)
• 5. Диагонали ромба точкой пересечения делятся пополам ( small ( AO = OC, ) ( small BO=OD).)

Ромб имеет также и следующие свойства:

• 6. Диагонали ромба пересекаются под прямым углом (( small AC perp BD.) )
• 7. Диагонали ромба являются биссектрисами его углов (( small angle ABD = angle CBD, ) ( small angle ADB = angle CDB, ) ( small angle DAC = angle BAC, ) ( small angle BCA = angle DCA. ))
• 8. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
• 9. Сумма квадратов диагоналей ромба равна квадрату стороны, умноженная на четыре ( small (AC^2+BD^2=4AB^2). )

Докажем свойства 6 и 7, сформулировав следующую теорему:

Теорема 1. Диагонали ромба перпендикулярны и являются биссектрисами его углов.

Доказательство. По определению 1, ( small AD = DC ) (Рис.2). Следовательно треугольник ( small DAC ) равнобедренный. Тогда ( small angle DCO = angle DAO. ) Учитывая, что ( small AO = OC ) (свойство 5 ромба), получим, что треугольники ( small DOA ) и ( small DOC ) равны по двум сторонам и углу между ними (см. статью Треугольники. Признаки равенства треугольников). Тогда равны углы DOC и DOA. Но эти углы смежные и их сумма равна 180°. Следовательно ( small angle DOC= angle DOA=90°. ) То есть диагонали AC и BD перпендикулярны.

Из равенства треугольников ( small DOA ) и ( small DOC ) также следует, что ( small angle CDO= angle ADO,) следовательно BD является биссектрисой угла ADС, то есть BD является биссектрисой ромба ABCD.

Признаки ромба

Признак 1. Если смежные стороны параллелограмма равны, то этот параллелограмм − ромб.

Доказательство. Пусть смежные стороны параллелограмма ABCD равны. То есть имеем: AB=BC (Рис.3). У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда DC=AB=BC=AD. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 2. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм − ромб.

Доказательство. Пусть диагонали параллелограмма ABCD перпендикулярны (Рис.3). Рассмотрим прямоугольные треугольники AOB и COB. Так как у параллелограмма диагонали точкой пересечения разделяются пополам (Свойство 2 статьи Параллелограмм), то AO=OC. Тогда прямоугольные треугольники AOB и COB равны по двум катетам (AO=OC, BO общий катет (см. статью Прямоугольный треугольник. Свойства, признаки равенства)). Следовательно AB=BC. Тогда по признаку 1 этот параллелограмм является ромбом.

Признак 3. Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм − ромб.

Доказательство. Пусть диагональ AC параллелограмма ABCD является биссектрисой угла BAD (Рис.4). Тогда ( small angle 1= angle 2 .) У параллелограмма ABCD ( small AB || DC .) Тогда для параллельных прямых AB и DC и секущей AC справедливо равенство ( small angle 1= angle 4 .) (см теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично, для параллельных прямых BC и AD и секущей AC справедливо равенство ( small angle 2= angle 3 .) Так как ( small angle 1= angle 2 ,) то ( small angle 1= angle 2=angle 3= angle 4 .) Из ( small angle 1= angle 3) следует, что треугольник ABC равнобедренный (Признак 2 статьи Равнобедренный треугольник). Тогда AB=BC. У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда AB=BC=CD=DA. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 4. Если стороны четырехугольника равны, то этот четырехугольник − ромб.

Доказательство. Пусть у четырехугольника все стороны равны. Тогда этот четырехугольник является параллелограммом (признак 2 статьи Параллелограмм). А по определению 1, этот параллелограмм является ромбом.