Задачи на движение навстречу друг другу (встречное движение) — один из трех основных видов задач на движение.
Если два объекта движутся навстречу друг другу, то они сближаются:
Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:
Скорость сближения больше, чем скорость каждого из них.
Скорость, время и расстояние связаны между собой формулой пути:
Рассмотрим некоторые задачи на встречное движение.
Задача 1
Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?
Решение:
Условие задач на движение удобно оформлять в виде таблицы:
|
v, км/ч |
t, ч |
s, км |
|
|
I велосипедист |
12 |
3 |
? |
|
II велосипедист |
10 |
3 |
? |
1) 12+10=22 (км/ч) скорость сближения велосипедистов
2) 22∙3=66 (км) было между велосипедистами в начале пути.
Ответ: 66 км.
Задача 2
Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого — 60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?
Решение:
|
v, км/ч |
t, ч |
s, км |
|
|
I поезд |
60 |
? |
? |
|
II поезд |
50 |
? |
? |
1) 60+50=110 (км/ч) скорость сближения поездов
2) 440:110=4 (ч) время, через которое поезда встретятся.
Ответ: через 4 ч.
Задача 3.
Два пешехода находились на расстоянии 20 км друг от друга. Они вышли одновременно навстречу друг другу и встретились через 2 часа. Скорость одного пешехода 6 км/ч. Найти скорость другого пешехода.
|
v, км/ч |
t, ч |
s, км |
|
|
I пешеход |
6 |
2 |
? |
|
II пешеход |
? |
2 |
? |
1) 20:2=10 (км/ч) скорость сближения пешеходов
2) 10-6=4 (км/ч) скорость другого пешехода.
Ответ: 4 км/ч.
Цели урока:
1. Вывести формулу зависимости между величинами
расстояние, скорость сближения и время встречи
через решение задач.
2. Закрепить умение анализировать и решать
задачи.
3. Развивать логическое мышление, речь, навыки
устных и письменных вычислений, самоанализа и
самоконтроля, воспитание любви к малой Родине.
Оборудование: учебник математики
Л.Г.Петерсон, карточки разного цвета с числами,
чертежи, магический квадрат, презентация,
алгоритм анализа задачи, карточки с
математическими понятиями.
ХОД УРОКА
1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ.
Каждый день – всегда, везде,
На занятиях, в игре,
Смело, чётко говорим
И тихонечко сидим.
– Пожелаем друг другу удачи и хорошего
настроения.
2. АКТУАЛИЗАЦИЯ ЗНАНИЙ.
– На любом уроке, в любом деле нам необходимо
внимание, поэтому мы начнём наш урок с игры «Кто
самый внимательный?»
– Я буду показывать вам два числа. Если они
записаны на красном фоне, то их надо сложить; если
на синем, то вычесть; если на зелёном, то умножить;
если на жёлтом, то разделить. В тетрадь надо
записывать только ответы в строчку через
запятую.
39 и 13 – жёлтый 39:13=3
240 и 40 – жёлтый 240:40=6
23 и 14 – синий 23–14=9
60 и 5 – жёлтый 60:5=12
150 и 10 – жёлтый 150:10=15
400 и 382 – синий 400–382=18
90 и 69 – синий 90–69=21
18 и 9 – красный 18+9=27
17 и 2 – зелёный 17х2=34
– Назовите ответы. Проверим, кто из вас
внимательный.
(Открыть доску.)
– Сравните ряд чисел у вас в тетради и ряд на
доске.
34,27,21,18,15,12,9,6,3.
– Что общего? Чем отличаются?
– Эти числа записаны у вас на квадратах.
Определите – квадрат магический? Давайте
вспомним признаки магического квадрата. (Работа
в группах.)
– Можно этот квадрат назвать магическим?
Почему?
– Работая в группах, вы должны превратить
квадрат в магический, изменив лишь одно число.
– Сегодня на уроке мы с помощью этого
магического квадрата отправимся в путешествие
по родному краю. Чтобы всё успеть, нам надо точно
рассчитать время и скорость на каждом участке
пути, уметь «читать »чертежи, знать понятия,
связанные с движением. Какие понятия нам
пригодятся?
– Итак, мы отправляемся в путешествие по
родному Пермскому краю. (Приложение.
Слайд 1).
Карта маршрута перед вами. Начинаем свой путь
из города Перми. Как мы ехали из Перми в Карагай,
расскажет таблица.
| объект | скорость | время | расстояние |
| автобус | 55 км/ч | 2 ч | ? км |
– Составьте задачу. Какая формула потребуется
для решения задачи?
– Назовите решение и ответ задачи.
– Преодолев 110 км, мы очутились в Карагае. (Приложение. Слайд 2).
В этом населённом пункте нам предстоит решить
задачу.
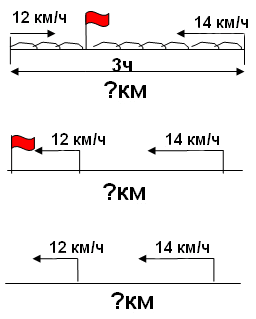
Два велосипедиста едут навстречу друг другу.
скорость одного 12 км/ч, а скорость другого 14 км/ч.
Они встретились через 3 часа. Какое расстояние
было между ними первоначально?
– Выберите чертёж, который соответствует
данной задаче. (Открыть доску.)
Рис. 1
Обоснуйте ответ. Решите задачу устно, составив
план действий.
1) 12х3=36 (км) – расстояние 1.
2) 14х3=42 (км) – расстояние 2.
3) 36+42=78 (км)
Ответ: 78 км было между ними первоначально.
– Есть ли другой способ решения задачи?
(поставлена ПРОБЛЕМА)
– Определите тему урока. Поставьте цель. Чего
вы хотите достичь? (Научиться решать задачи на
встречное движение разными способами.)
3. ОТКРЫТИЕ НОВОГО ЗНАНИЯ.
ФОРМУЛА ЗАВИСИМОСТИ МЕЖДУ ВЕЛИЧИНАМИ В ЗАДАЧЕ
НА ВСТРЕЧНОЕ ДВИЖЕНИЕ.
– Чтобы нам очутиться в следующем населённом
пункте Коса, необходимо рассчитать время
движения автобуса. Перед вами таблица.
|
объект |
скорость |
время |
Расстояние |
|
автобус |
50 км/ч |
? ч |
200 км |
– Знание какой формулы понадобится для решения
этой задачи?
200:50=4 (ч)
– Через 4 часа мы очутились в Косе. (Приложение.
Слайд 3).
В этом населённом пункте нам предстоит
ответственная работа. Открываем учебник
математики на стр. 89, посмотрим на чертёж к
заданию № 1.составим рассказ по нему, (рассказ
детей.)
– А сейчас проверьте себя, прочитав условие
задачи. Назовите вопросы к ней.
Ответьте на первый вопрос. (Двое работают у
доски, задание учебника вынесено на доску.)
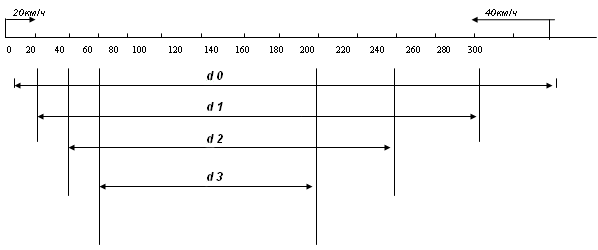
Рис. 2
| Время, ч | Расстояние между объектами |
| 0 | 300 |
| 1 | 300–(20+40)х1=240 |
| 2 | 300–(20+40)х2= |
| 3 | |
| 4 | |
| 5 | |
– Объясните, почему все формулы начинаются с
числа 300? Что оно обозначает? Почему вы выбрали
знак «–»? Что обозначает выражение в скобках? Что
мы называем скоростью сближения? Как её найти при
встречном движении? Что обозначает «х2, 3, 4, 5»?
– Так как же найти расстояние между объектами,
движущимися навстречу друг другу?
(ОТКРЫТИЕ) ЧТОБЫ НАЙТИ ПЕРВОНАЧАЛЬНОЕ
РАССТОЯНИЕ МЕЖДУ ОБЪЕКТАМИ ПРИ ВСТРЕЧНОМ
ДВИЖЕНИИ, МОЖНО СКОРОСТЬ СБЛИЖЕНИЯ УМНОЖИТЬ НА
ВРЕМЯ.
(Вывесить на доску новые формулы.)
S= (V1 + V2) х tвст.
S= Vсбл. х tвст.
4. ПЕРВИЧНОЕ ЗАКРЕПЛЕНИЕ.
– А сейчас вернёмся к задаче о двух
велосипедистах.
– Как же можно её решить другим способом?
1) Вычислить скорость сближения.
12+14=26 (км/ч)
2) Найти первоначальное расстояние между ними.
26х3=78 (км)
5. ФИЗКУЛЬТМИНУТКА.
– Прежде чем сесть в автобус и отправиться в
обратный путь, давайте немного отдохнём.
Встаньте все из-за парт. Перед вами число.
Назовите его.
7003204
Столько раз поднимем руки, сколько единиц в
классе тысяч. (3)
Столько выполним наклонов, сколько единиц в
классе миллионов. (7)
И присядем столько раз, сколько сотен в классе
единиц. (2)
На носочки встанем,
Потолок достанем
И тихонько сядем.
6. ЗАКРЕПЛЕНИЕ.
САМОСТОЯТЕЛЬНАЯ РАБОТА
– Итак, мы на обратном пути. Чтобы нам добраться
до Перми, нужно определить скорость движения
нашего автобуса. Перед вами таблица. Попробуйте
найти скорость автобуса. Что для этого нужно
вспомнить?
| объект | скорость | время | расстояние |
| автобус | ?км/ч | 5ч | 310км |
310:5=62 км/ч
– Автобус тронулся, а мы с вами, чтобы было не
скучно, попробуем самостоятельно решить задачу
№ 3 на стр. 90.
В тетрадь при решении задачи вносить формулы,
которые необходимы для её решения. Можно
пользоваться алгоритмом решения задач, который
находится перед вами.
1) 9+7=16 (км/ч) – скорость сближения
2) 16х2=32 (км)
Ответ: 32 км расстояние между сёлами.
(Проверка по доске.)
7. ИТОГ УРОКА.
– Вот и закончилось наше путешествие по краю.
Надеюсь, что это путешествие было для вас
познавательным. Достигли вы той цели, которую
поставили перед собой на уроке? Прогуляемся по
тропинке знаний (на доске).
Рис. 3
И напоследок, расставьте знаки действий:
S= (V1 … V2 ) … tвст.
S= Vсбл. … tвст.
8. ДОМАШНЕЕ ЗАДАНИЕ.
Стр. 90, № 2, 10.
–
Миша, что случилось? Ты чего такой грустный?
–
Я не могу решить задачу по математике. Она очень сложная. И я не знаю к кому
мне обратиться за помощью.
–
Если хочешь, я могу тебе помочь. Я люблю решать сложные задачи.
–
Поможешь, правда?! Тогда слушай задачу.
Два
велосипедиста выехали одновременно навстречу друг другу из двух спортивных
лагерей и встретились через 3 часа. Первый велосипедист ехал со скоростью 15
км/ч, а второй со скоростью 17 км/ч. Найдите расстояние между спортивными
лагерями.
–
Так это же задача на встречное движение, обрати внимание «выехали
одновременно навстречу друг другу». Ну, давай разбираться.
Давай
выполним рисунок к этой задаче.
Итак,
обозначим расстояние между двумя спортивными лагерями отрезком. Первый лагерь
обозначим буквой А, стрелочкой укажем направление, в котором едет первый
велосипедист и укажем его скорость. Второй лагерь обозначим буквой В,
так же укажем направление движения и скорость второго
велосипедиста. Теперь мы хорошо видим, что движение у нас встречное.
Так же мы знаем, что через 3 часа они встретятся. Нам надо узнать, сколько
всего км между двумя лагерями.
За
час первый велосипедист проехал 15 км, ещё час и ещё 15 км, третий час и снова
15 км. Он доехал до места, где встретился со вторым велосипедистом.
Что
же мы можем узнать?
–
Мы можем узнать, сколько же км проехал первый велосипедист за 3 часа.
1)
15 ·
3 = 45 км.
–
Молодец, правильно. Но, второй велосипедист в это время тоже не стоял, а ехал.
Его
скорость 17 км/ч, значит за каждый из трёх часов до встречи с первый
велосипедистом он проезжал по 17 км. – И мы
2)
17 ·
3 = 51 км.
Итак,
до встречи первый велосипедист проехал 45 км, а второй 51 км.
–
И теперь мы можем узнать, сколько всего км проехали велосипедисты до встречи.
3)
45 + 51 = 96 км. Всего проехали велосипедисты. Значит, расстояние между
лагерями 96 км.
Ответ:
расстояние между лагерями 96 км.
–
Мы посмотрели, как двигались велосипедисты, но ведь они на самом деле двигались
не поочерёдно, а одновременно.
–
Значит, для решения этой задачи существует и другой способ, да?
–
Да, есть и другой способ решения этой задачи. Давай вернёмся к нашему рисунку.
Прошёл
час, за это время первый проехал 15 км, а второй в это же время ехал ему
навстречу и за час проехал 17 км.
Значит,
они приблизились друг к другу на сумму двух этих чисел. Поэтому мы можем
узнать, на сколько километров за час велосипедисты стали ближе друг к другу.
1)
15 + 17 = 32 км/ч. Т.к. это сближение произошло за один час, то число 32 является
скоростью сближения.
–
Повтори, пожалуйста, что такое скорость сближения?
–
Это сумма скоростей двух приближающихся друг к другу объектов.
–
Так, понятно. Значит, если за первый час два велосипедиста стали ближе друг к
другу на 32 км и скорость их движения не меняется, значит, за второй час они
приблизятся ещё на 32 км и за третий час – тоже на 32 км.
Вот
велосипедисты и встретились. Они до встречи ехали 3 часа, приближаясь за каждый
час на 32 км. Поэтому мы
2)
32 ·
3 = 96 км.
Ответ:
расстояние между лагерями 96 км.
–
Давай ещё раз посмотрим внимательно на оба способа решения этой задачи.
В
первом способе мы сначала узнали, сколько км проехал
до встречи первый велосипедист, затем узнали, сколько проехал второй
велосипедист и после этого нашли всё расстояние между лагерями.
Во
втором способе мы сразу узнали, на сколько км за
каждый час приближались друг к другу оба велосипедиста, т.е. скорость
сближения. А вторым действием узнавали весь пройдённый путь.
–
Да, так интересно. Задача одна, а решения два.
–
А что ты запомнил, при решении таких задач?
–
Если нам надо найти расстояние, для этого мы скорость умножаем на время.
–
Правильно, а ещё, т.к. расстояние было пройдено не одним велосипедистом, а
двумя вместе, и двигались они на встречу друг другу, то можно использовать
такую величину, как скорость сближения. А что такое скорость
сближения?
–
Это сумма скоростей двух приближающихся друг к другу объектов. В
этой задаче такими объектами были велосипедисты.
Ура!
Теперь я умею решать задачи на встречное движение. Надеюсь и вы тоже!
Задачи на встречное движение
Рассмотрим задачи, в которых речь идёт о встречном движении. В таких задачах два каких-нибудь объекта движутся навстречу друг другу. Задачи на встречное движение можно решать двумя способами.
Задача 1. Два автомобиля выехали одновременно из двух населённых пунктов и встретились через 4 часа. Первый автомобиль ехал со скоростью 100 км/ч, а второй — со скоростью 70 км/ч. На каком расстоянии друг от друга находятся населённые пункты?
Решение: Из условия задачи известны скорость каждого автомобиля и время, которое автомобили были в пути. Значит, можно найти расстояние, которое проехал каждый автомобиль до встречи. Для этого нужно скорость умножить на время:
1) 100 · 4 = 400 (км) — проехал первый автомобиль,
2) 70 · 4 = 280 (км) — проехал второй автомобиль.
Найдя сумму полученных результатов, узнаем расстояние между населёнными пунктами:
400 + 280 = 680 (км).
Данную задачу можно решить и другим способом. Каждый час расстояние между автомобилями сокращалось на 170 километров (100 + 70), 170 км/ч — это скорость сближения автомобилей. За 4 часа они проехали расстояние:
170 · 4 = 680 (км).
Таким образом, задачу на встречное движение можно решить двумя способами:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 100 · 4 = 400 (км) | 1) 100 + 70 = 170 (км/ч) |
| 2) 70 · 4 = 280 (км) | 2) 170 · 4 = 680 (км) |
| 3) 400 + 280 = 680 (км) |
Ответ: Населённые пункты находятся на расстоянии 680 км.
Задача 2. Из двух посёлков навстречу друг другу вышли одновременно два пешехода. Скорость первого пешехода 4 км/ч, а скорость второго пешехода 5 км/ч. Какое расстояние будет между пешеходами через 5 часов после выхода, если расстояние между посёлками 70 км?
Решение: Сначала можно определить сколько километров прошёл каждый из пешеходов за 5 часов, для этого скорость пешеходов умножим на 5:
1) 4 · 5 = 20 (км) — прошёл первый пешеход,
2) 5 · 5 = 25 (км) — прошёл второй пешеход.
Затем можно найти общий путь, пройденный двумя пешеходами за 5 часов:
20 + 25 = 45 (км).
Теперь можно найти расстояние между пешеходами, отняв от общего расстояния между посёлками 45 уже пройденных километров:
70 — 45 = 25 (км).
У данной задачи есть и второй вариант решения. Можно сначала найти скорость сближения пешеходов:
4 + 5 = 9 (км/ч).
Затем найти пройденное расстояние, умножив скорость сближения (9 км/ч) на время движения пешеходов (5 ч):
9 · 5 = 45 (км).
А теперь, для нахождения расстояния между пешеходами, вычесть пройденное расстояние (45 км) из общего:
70 — 45 = 25 (км).
Таким образом, данная задача имеет два варианта решения:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 4 · 5 = 20 (км) | 1) 4 + 5 = 9 (км/ч) |
| 2) 5 · 5 = 25 (км) | 2) 9 · 5 = 45 (км) |
| 3) 20 + 25 = 45 (км) | 3) 70 — 45 = 25 (км) |
| 4) 70 — 45 = 25 (км) |
Ответ: Через 5 часов расстояние между пешеходами будет 25 км.
Чтобы решать задачи на встречное движение, вспомним основные понятия и формулы для решения задач на движение:
(v) — скорость;
и
v2
— скорость первого и второго объектов;
— скорость сближения;
(t) — время;
— время до встречи;
(s) — первоначальное расстояние;
— расстояние между объектами через определённый промежуток времени после начала движения объектов.
Рассмотрим первую ситуацию.
Яра и Юра давно не виделись и договорились встретиться в парке. Расстояние между друзьями составляет (315) км. Юра поехал на автомобиле со скоростью (60) км/ч, а Яра — на автобусе со скоростью (45) км/ч.
Через какое время друзья встретятся?
Начертим схему.
Стрелки на схеме показывают, с какой скоростью едут Юра и Яра. Флажком обозначено место встречи друзей. А дугой показано расстояние между героями — (315) км.
По схеме видно, что друзья едут навстречу друг другу, то есть расстояние между ними сокращается. Перед нами — встречное движение.
Первоначально необходимо найти скорость сближения по формуле:
1. (60 + 45 = 105) км/ч.
Теперь найдём, через какое время произойдёт встреча Юры и Яры:
2. (315 : 105 = 3) ч.
Ответ: через (3) часа друзья встретятся в парке.
Рассмотрим вторую ситуацию.
С двух станций одновременно начали движение два поезда навстречу друг другу. Скорость первого поезда равна (90) км/ ч, а второго — (70) км/ч. Чему равно расстояние между станциями, если встреча поездов произошла через (2) часа после начала отправления?
Начертим схему.
Найдём скорость сближения двух поездов: (90 + 70 = 160) км/ч.
Определим расстояние между станциями до начала отправления поездов: (160 · 2 = 320) км.
Ответ: расстояние между станциями составляет (320) км.
Рассмотрим третью ситуацию.
Тракторист и таксист едут навстречу друг другу из двух сёл, расстояние между которыми составляет (400) км. Скорость трактора — (25) км/ ч, а такси — (50) км/ч. Как изменится расстояние между ними через (1) час? Через (2) часа? Через (4) часа?
Заполним таблицу:
|
(t) ч |
(d) км |
|
(0) |
(400) |
|
(1) |
(400) (– (25 + 50) · 1 = 325) |
|
(2) |
(400) (– (25 + 50) · 2 = 250) |
|
(4) |
(400) (– (25 + 50) · 4 = 100) |
Источники:
Изображения: схема, робот, космонавт, транспорт. © ЯКласс.