Содержание:
-
Хотите научиться решать задания на простые проценты?
-
Условие задачи
-
Решение задачи
-
Выводы и рекомендации
-
Примеры условий реальных заданий на простые проценты, встречающихся на ЕГЭ по математике
-
Хотите стать профессиональным решателем заданий на простые проценты? Записывайтесь ко мне на индивидуальную подготовку!
Хотите научиться решать задания на простые проценты?
Привет! Меня зовут Александр Георгиевич. Мне $35+$ лет. Я — профессиональный репетитор по математике и информатике. Уже на протяжении $10+$ лет готовлю школьников $9-11$-ых классов к успешной сдаче ЕГЭ по математике/информатике.
На официальном экзамене ЕГЭ по математике вас в обязательном порядке поджидает задача из экономического блока. Есть неплохая вероятность, что попадется задание на простые проценты. В данной статье хочу показать вам решение подобного задания.
Несмотря на то, что вы крайне занятой человек, ценящий собственное время, настоятельно рекомендую вам потратить буквально $2-3$ минуты и познакомиться с отзывами моих учеников. Все они достигли поставленных целей и набрали высокие баллы на рубежном контроле ЕГЭ.
Для записи ко мне на частную подготовку позвоните по телефону, указанному в шапке данного сайта. Приготовьте любые уточняющие вопросы. Жду вас на первом пробном занятии.
Условие задачи
Вкладчик открыл счет в банке. Процентная ставка по банковским вкладам составляет (8%) в год. Через (3) года на счете вкладчика сформировалась сумма размером (310,000) рублей.
Определить первоначальный банковский вклад (в рублях).
Решение задачи
Если внимательно прочитать условие задачи, то сразу заметно, что нет никаких фраз-маркеров, указывающих на то, что это задание на простые проценты. В общем постановка задачи оставляет желать лучшего! Но, очевидно, что в данном случае нет никакой капитализации процентов, следовательно, применим схему простых процентов.
Давайте введем следующие обозначения:
| $V_{старт}$ — размер первоначального вклада | $q$ — ставка банка, выраженная в процентах | $r = frac{q}{100}$ — процентная ставка банка, выраженная в долях |
| $V_{конец}$ — размер конечного вклада | (n) — общее количество отчетных периодов | (i) — номер текущего отчетного периода |
Эти обозначения используются во всех моих заданиях на простые проценты. Это очень удобно, читателю достаточно просто переключаться между различными решениями, не теряя сути математических выкладок.
Из условия вытекает, что:
| $V_{конец} = 310 000$, руб. | $q = 8%$ | $n = 3$, лет. | $V_{старт} = ?$ |
Наша цель — определить размер первоначального банковского вклада, выраженный в рублях. Гораздо чаще на экзамене просят выяснить размер конечного вклада! Будьте внимательны при чтении формулировки задания.
В заданиях на простые проценты все упирается в одну единственную формулу. Какую? Ее получение было мною детально описано, когда разрабатывалась математическая модель простых процентов. Не в курсе, что это за модель? Срочно бегите ее изучать, исследовать, зубрить!
$V_{конец} = V_{старт} * (1 + n * r)$ — главная формула схемы простых процентов.
Важно! Когда будете сдавать ЕГЭ по математике, постарайтесь, хотя бы в сокращенной форме, продемонстрировать вывод математической модели простых процентов. Иначе можете не досчитаться баллов, даже, несмотря на то, что получите абсолютно правильный ответ. Будет очень досадно!
Поскольку в формуле фигурирует переменная $r$, а не $q$, то давайте выполним соответствующий перевод: $r = frac{q}{100%} = frac{8%}{100%} = 0.08$.
Кстати, а нам ведь в вышеприведенной зависимости все известно, кроме переменной $V_{старт}$, следовательно, составим и решим следующее незамысловатое линейное уравнение:
$310 000 = V_{старт} * (1 + 3 * 0.08)$
$V_{старт} = frac{310 000}{1.24}$
Чтобы правильно разделить без калькулятора эти неудобные числа, давайте разложим их на некоторые делители и попробуем потом сократить:
$310 000 = 31 * 10 000$ — пока так, хотя это неполное разложение, разумеется.
$1.24 = frac{124}{100} = frac{31 * 4}{4 * 25} = frac{31}{25}$
Собираем все воедино:
$V_{старт} = (31 * 10 000) : frac{31}{25}$
$V_{старт} = frac{31 * 10 000 * 25}{31}$
$V_{старт} = 10 000 * 25$
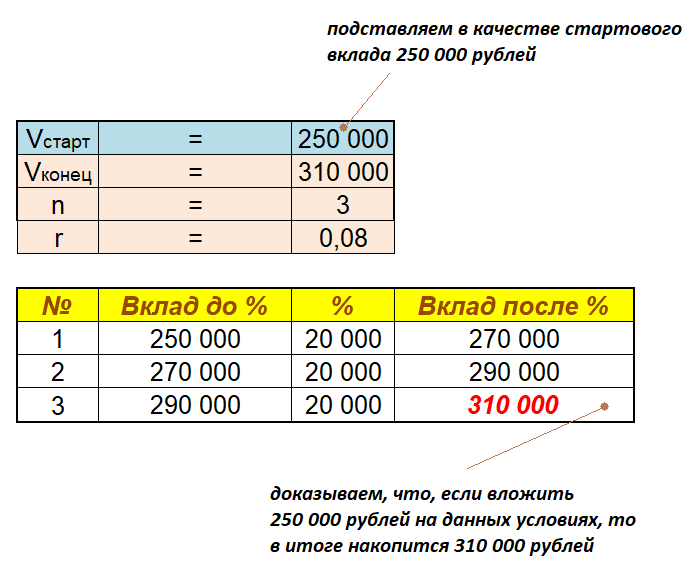
$V_{старт} = 250 000$, рублей.
Готово! Решили! Это значение и будет выписано в качестве официального ответа. Давайте сейчас проведем верификацию в программе «MS Excel«.
Ответ: $250 000$
Выводы и рекомендации
Задания на простые проценты не покажутся вам сложными, и вы с ними легко справитесь, если:
-
не перепутаете схему простых процентов со схемой сложных процентов;
-
хорошо знаете математическую модель простых процентов.
Это, пожалуй, главные факторы, влияющие на успешность решения подобных заданий!
Примеры условий реальных заданий на простые проценты, встречающихся на ЕГЭ по математике
А сейчас пришло время вам немного поработать самостоятельно. Нужно ведь закрепить пройденный материал. Если что-то не будет получаться — ничего страшного в этом нет. Переходите по ссылке «Перейти к текстовому решению» и внимательно знакомьтесь с моим решением.
|
Задача №1 Вкладчик поместил сумму размером (80,000) рублей в банк. Процентная ставка банка по вкладам составляет (9%) в год. Схема вложений денег не предполагает капитализацию процентов. Определить, какого размера станет вклад через (6) лет? Перейти к текстовому решению |
|
Задача №2 Вкладчик поместил сумму размером (300,000) рублей в банк. В договоре прописано, что схема начисления процентов на депозит не предполагает их капитализации. Через (9) лет на его балансе образовалось сумма в размере (516,000) рублей. Определить процентную ставку банка по вкладу. Перейти к текстовому решению |
|
Задача №3 Вкладчик открыл счет в банке. Процентная ставка по банковским вкладам составляет (8%) в год. Через (3) года на счете вкладчика сформировалась сумма размером (310,000) рублей. Определить первоначальный банковский вклад (в рублях). Перейти к текстовому решению |
Также вы можете написать мне на почту и задать какие-либо уточняющие вопросы по данным заданиям на простые проценты. Или публикуйте свои вопросы в комментариях к данной статье. Я постараюсь максимально оперативно ответить!
Данный список задач я регулярно обновляю и дополняю, поэтому, рекомендую периодически сюда заглядывать.
Хотите стать профессиональным решателем заданий на простые проценты? Записывайтесь ко мне на индивидуальную подготовку!
Скажу честно, задания из экономического блока ЕГЭ по математике мне импонируют. На своих частных уроках показываю эффективные методики решения всевозможных задач финансовой направленности. Решаем с учеником не только задания на простые проценты, а в том числе и задачи на кредиты, на вклады, про акции, оптимизационного характера, смешанного типа.
Я — репетитор-практик! Это означает, что на частных занятиях мы решаем, решаем и еще раз решаем! Теория без практики мертва на $100%$. Львиную долю урока я посвящаю исключительно практической деятельности. Теоретического материала предостаточно в сети Интернет, да, не всегда полного и адекватного, но, в целом, найти можно, что угодно.
Не забывайте подписываться на мой Youtube-канал, посвященный математике, информатике, программированию, алгоритмам и базам данных. Также регулярно проходят образовательные стримы на twitch-канале. И, пожалуй, подпишитесь на рассылку, чтобы в числе первых узнавать о новых публикуемых материалах.
Ко мне поступает множество заявок на персональное обучение в любое время года, но я физически не могу всем помочь. Поэтому, не откладывайте свое решение в долгий ящик, а действуйте прямо сейчас. Звоните мне по мобильному номеру, задавайте тематические уточняющие вопросы и записывайтесь на первый пробный урок.
Я готов начать решать задания на простые проценты прямо сейчас! А вы готовы начать свой успешный путь?






Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
Задача 1
В банке был сделан вклад сроком на 1 год под 4% годовых. По окончанию срока была получена сумма в размере 35 200 рублей. Определить первоначальную сумму вклада.
Решение:
Необходим расчет первоначальной суммы вклада, следовательно, используем функцию ПС (рис.1):
Рисунок 1 Диалоговое окно функции ПС
Первоначальная сумма вклада равна 33846,2 руб.
Аргументы функции ПС описаны ниже.
- Ставка — Обязательный. Процентная ставка за период. Например, если получен кредит на автомобиль под 10 процентов годовых и выплаты производятся ежемесячно, процентная ставка за месяц составит 10%/12 (0,83%). В качестве значения аргумента «ставка» нужно ввести в формулу 10%/12, 0,83% или 0,0083.
- Кпер — Обязательный. Общее число периодов платежей для ежегодного платежа. Например, если получен кредит на 4 года на покупку автомобиля и платежи производятся ежемесячно, то кредит имеет 4*12 (или 48) периодов. В качестве значения аргумента «кпер» в формулу нужно ввести число 48.
- Предприятие получило в банке кредит 6 млн. руб. под 9% годовых, сроком на 1 месяц. Определить наращенную сумму, которую предприятие должно вернуть банку
- Рассчитайте оборачиваемость активов и годовой объем продаж, которые необходимо обеспечить для достижения запланированного уровня рентабельности активов универмага и оптовой
- Товарооборот и основные средства. Показатели План Факт Товарооборот, тыс. руб. 27 000 29140 Среднегодовая стоимость основных средств, тыс. руб.
- Товарооборот и основные средства. Показатели Прошлый год Отчётный год Товарооборот, тыс. руб. 65700 66000 Среднегодовая первоначальная стоимость основных средств, тыс. руб.
Что нужно знать при расчете процентов по вкладам (депозитам)
Рано или поздно перед нами встает вопрос о расчете процентов по банковским вкладам (депозитам).
В банковском деле существует два способа начисления процентов:
- по формуле простых процентов;
- по формуле сложных процентов.
Расчет процентов по формулам может совершаться с использованием плавающей и фиксированной процентной ставки.
Фиксированная ставка — процентная ставка, которая остается постоянной на весь срок размещения вклада. Как правило, ставка может быть изменена в момент пролонгации (продления) договора, выплате процентов при досрочном расторжении договора.
Плавающая ставка — процентная ставка, которая может меняться во время размещения вклада. Условия и порядок изменения ставки оговариваются в договоре (например, такими условиями могут быть изменение ставки рефинансирования, изменение курсов валют и т.п.).
Для того, чтобы начать расчет, нам необходимо знать следующие параметры депозита:
- сумма вклада;
- годовая процентная ставка;
- период начисления процентов по депозиту;
- срок размещения депозиа;
- вид процентной ставки — фиксированная или плавающая.
Формула начисления простых процентов
Расчет наращенной суммы вклада
Данной формулой необходимо воспользоваться если начисление процентов происходит в конце действия депозита.
S = P × (1 + n × i),
где S — наращенная сумма;
P — сумма вклада (первоначальная сумма);
n — период размещения вклада;
i — годовая процентная ставка.
Пример расчета наращенной суммы по формуле простых процентов
Первоначальная сумма вклада P = 45000 руб. помещена в банк на n = 2 года под i = 15% годовых. Определим наращенную сумму после двух лет
S = 45000 × (1 + 2 × 0,15) = 58500 руб.
Следовательно, за два года размещения вклада в данном случает доход составит 13500 руб.
Расчет периода начисления вклада
Зная первоначальную сумму вклада P, наращенную сумму S, простую годовую процентную ставку i, можно определить период начисления
n = (S — P)/(i × P).
Данной формулой возможно воспользоваться, например, в случае расчета времени начисления необходимой нам суммы.
Пример расчета периода начисления по формуле простых процентов
Первоначальная сумма P = 10000 руб., необходимо нарастить сумму S до 20000 руб., i = 20% годовых. Определим какой период времени нам понадобится для получения 20000 руб.
n = (20000 — 10000)/(0,2 × 20000) = 2,5 года.
Определение простой годовой процентной ставки
Чтобы определить необходимую нам процентную ставку воспользуемся формулой
i = (S — P)/(n × P).
Пример расчета простой процентной ставки
Имеем первоначальную сумму 30000 руб., необходимо ее нарастить (заработать) до 35000 руб, предполагаем разместить на 1 год. Определим необходимую нам процентную ставку
i = (35000 — 30000)/(1 × 30000) = 16,7%.
Расчет наращенной суммы при плавающей процентной ставки
Если процентная ставка по депозиту менялась в течении срока размещения, то воспользуемся формулой
S = P × (1 + n1 × i1 + n2 × i2 + … + n k × ik).
Пример расчета наращенной суммы при плавающей процентной ставки
Первоначальная сумма вклада P = 75000 руб., в первой половине года применялась простая процентная ставка 7,5% годовых, во второй половине года — 9,5% годовых. Определим наращенную сумму по вкладу в конце года
S = 75000 × (1 + 0,5 × 0,075 + 0,5 × 0,095) = 81375 руб.
Формула начисления сложных процентов
Формула сложных процентов применяется при капитализации процентов (начисления процентов на проценты), т.е. начисление процентов по депозиту происходит через равные промежутки времени, а начисленные проценты прибавляются ко вкладу.
Расчет наращенной суммы вклада (сложные проценты)
Наращенная сумма при периоде начисления в годах определяется
S = P × (1 + i)n.
Пример расчета наращенной суммы при сложных процентах
Первоначальная сумма вклада P = 25000 руб., помещена в банк на n = 3 года под i = 7,5% годовых. Определим наращенную сумму
S = 25000 × (1 + 0,075)3 = 31057 руб.
Расчет периода начисления в годах при сложных процентах
Если мы знаем первоначальную сумму вклада P, наращенную сумму S и сложную годовую процентную ставку i, то определим период начисления n (в годах) по формуле
n = ln(S/P)/ln(1 + i).
Пример расчета периода начисления при сложных процентах
Первоначальная сумма вклада P = 27500 руб., наращенная сумма S = 33700 руб., i = 10% годовых. Определим за какой период была начислена сумма
S = ln(33700/27500)/ln(1 + 0,1)= 2,1 года.
Расчет годовой процентной ставки при сложных процентах
Определить годовую процентную ставку при сложных процентах можно по формуле
i = n√S/P — 1.
Пример расчета годовой процентной ставки при сложных процентах
Первоначальная сумма вклада P = 75000 руб., наращенная сумма S = 97000 руб., период начисления n = 2 года. Определим процентную ставку
i = 2√97000/75000 — 1 =0,136 = 13,6%.
Расчет наращенной суммы при плавающей процентной ставки сложных процентов
S =P × (1 + i1)n1 × (1 + i2)n2 × … × (1 + in)nk
Пример расчета наращенной суммы при плавающей процентной ставки сложных процентов
Первоначальная сумма вклада P = 35000 руб., n1 = 2 года применялась сложная процентная ставка i1 = 10% годовых, затем n2 = 3 года применялась сложная процентная ставка i2 = 12% годовых. Определим наращенную сумму
S =35000 × (1 +0,1)2 × (1 +0,12)3 = 59498 руб.
Начисление сложных процентов несколько раз в году
Если начисление сложных процентов происходит несколько раз в году, то воспользуемся формулой
S = P × (1 + j/m)n×m
где j — номинальная процентная ставка; m — интервал начисления.
Пример начисление сложных процентов несколько раз в году
Первоначальная сумма инвестирования 62000 руб., период начисления 3 года, сложная процентная ставка j = 9% годовых ежеквартально, m = 4, т.к. в году 4 квартала. Определим наращенную сумму.
S = 62000 × (1 +0,09/4)3×4 = 80975 руб.
Загрузка…
Рассчитываем проценты по вкладу: формула и примеры
Чтобы выяснить, какой доход принесет вклад, недостаточно знать годовую ставку. На прибыльность также методика начисления банком процентов. В финансовой системе существуют понятия простого и сложного процента, позволяющего получить при почти равных условиях разный доход по вкладам.
Рассчитать проценты по вкладу можно самостоятельно без помощи специалиста. В статье разбираем особенности каждой схемы и объясняем, как работать с формулами.
Простые проценты
Это вознаграждение, которое начисляется на начальную сумму вклада за определенный период. Простые проценты не прибавляются к телу депозита и выплачиваются либо по истечении срока договора, либо раз в месяц или год по выбору вкладчика. Если договор продлевается на новый срок, то прибыль за предыдущий период также не суммируется с вкладом.
Такая методика начисления применяется, как правило, для вкладов с возможностью пополнения и снятия средств. Процентная ставка в этом случае ниже, чем при начислении сложных процентов. Это объясняется тем, что ваш вклад — финансовый инструмент получения прибыли банком. И чем меньше уверенности, что вы не заберете деньги раньше срока, тем ниже вероятность долгосрочного инвестирования капиталов банком, а значит — и ниже доход.
Сложные проценты или капитализация
В этом случае доход за оговоренный срок прибавляется к сумме вклада. В последующий период вознаграждение начисляется уже на увеличенный размер депозита. Сумма вклада постепенно растет за счет накапливаемых процентов, итоговый доход становится выше.
Срок капитализации — периодичность, с которой процент суммируется с текущим телом вклада. Банки добавляют проценты раз в месяц, квартал или день. Вам могут предложить депозит с плавающими ставками, когда процент увеличивается с течением времени. Как правило, процент повышается при увеличении срока хранения денег на депозите при условии, что снятий не было.
Доходность вкладов с капитализацией выше за счет увеличения тела кредита, однако наибольший доход дает тот депозит, по которому ограничено движение средств: запрещены снятия и пополнения, или дополнительные взносы разрешены, но с ограничением. Например, сумма всех пополнений не может превышать сумму открытия более, чем в 10 раз.
Расчет простых процентов
Выяснив годовую ставку, периоды и виды начисления процентов, можно посчитать доход по вкладу.
Простые проценты начисляются по следующей формуле:
где:
S — выплаченные проценты,
P — первоначальная сумма вложений,
I — годовая ставка,
T — количество дней вклада,
K — количество дней в году — 365 или 366.
Если вкладчик открыл депозит на 350 000 руб. сроком на 9 месяцев под 4,7%, процентный доход по вкладу составит:
Расчет сложных процентов
Чаще всего банки предлагают программы с ежемесячной капитализацией. Выбирая условия по вкладу, помните об общей закономерности: чем реже проценты прибавляются к телу депозита, тем меньше доход.
Ежедневная капитализация
Рассчитать доход за каждый день действия вклада поможет следующая формула:
где
Дв — сумма на конец срока, включая сумму открытия и начисленный процент,
Р — первоначальный размер депозита,
N — годовая процентная ставка, разделенная на 100,
К — количество дней в году — 365 или 366,
Т — срок вложения в днях.
Если клиент внес 350 000 руб. под 4,7% на 9 месяцев или 273 дня, в конце срока он получит:
Возвести число в большую степень можно на инженерном калькуляторе, где есть функция x^y, воспользоваться онлайн-сервисами или калькуляторами на сайтах банков.
Зная Дв, легко вычислить сумму процентов по вкладу за весь период:
Ежемесячная капитализация
Когда банк суммирует доход по депозиту раз в месяц, расчет ведется по формуле:
где:
Дв — итоговый доход, то есть размер вклада на конец срока включая сумму открытия и начисленный процент,
P — начальный депозит,
N — годовая ставка, разделенная на 100,
T — срок договора в месяцах.
Рассчитаем итоговую сумму с теми же исходными данными:
Процентный доход составит 12 532,56 ₽
Ежеквартальная капитализация
При начислении вознаграждения каждый квартал, а не раз в месяц, понадобится формула:
в ней Т — количество кварталов в сроке, остальные обозначения прежние.
Рассчитаем тот же вклад в конце срока:
Доход в виде процентов составит 12 483 ₽.
Но следует помнить: чем дольше срок размещения депозита, тем выше ставка. Поэтому при внесении денег на депозит надо сравнить условия с фактической ставкой, применяемой по выбранными вами условиям.
Итоги
Из таблицы видна разница доходов по методу простых и сложных процентов при равных условиях.
| Проценты по вкладу | Доход, руб. |
|---|---|
|
Простые |
12 303 |
|
Сложные: |
|
|
ежедневные |
12 521 |
|
ежемесячные |
12 532 |
|
ежеквартальные |
12 483 |
Однако нельзя однозначно утверждать о предпочтительности сложных процентов для каждого клиента. Оптимальная схема, тип банковского депозита — накопительный счет или вклад — зависят от ваших планов и потребностей:
- желаемый срок действия вклада и вероятность досрочного снятия средств
- необходимость регулярно пополнять счет или снимать средства
- необходимость регулярно снимать проценты
Если закрыт вклад до срока, вне зависимости от того, срочный он или до востребования, банк может применить санкции:
- Пересчитать процент по простой ставке до востребования. Законодательно ее размер не установлен, но большинство банков выплачивают всего 0,1–0,01%.
- Оставить половину или даже треть начальной ставки и тоже сделать перерасчет процентов.
Поэтому перед открытием депозита четко определите его срок и назначение. Райффайзен Банк предлагает банковские вклады без ограничений по снятию и пополнению, где проценты можно получать ежемесячно или добавлять к сумме депозита.
Эта страница полезна?
99
% клиентов считают страницу полезной
Следите за нами в соцсетях и в блоге
Данные для
расчета:
-
Банк предлагает
8% годовых -
Срок хранения 2
года -
Будущий вклад 5
тыс. 832 руб.
Ф
ормула:
Где:
К
– первоначальный вклад;
n
– годовая процентная ставка (или одного
начисления);
N
– количество лет (или количество
начислений по процентной ставке);
Кt
– размер вложенного капитала к концу
t
периода времени.
Решение:
Расчет первоначального
вклада при сложных процентах
Ответ:
Первоначальный
вклад должен составлять 5000 руб.
Задача № 5 Рассчитайте наращённую сумму капитала
Данные для
расчета:
-
Первоначальный
вклад 5 тыс. руб. -
Срок вклада 2 года
-
Банк предлагает
3 % годовых -
Начисление
процентов производится ежемесячно
Формула:
Где:
К
– первоначальный вклад;
n
– процентная ставка одного начисления;
N
– количество начислений по процентной
ставке;
Кt
– размер вложенного капитала к концу
t
периода времени.
Решение:
1) Расчет ежемесячной
процентной ставки
3% : 12 = 0.25 %
0.0025
2) Расчет количества
начислений по процентной ставке
2
12 = 24
3
)
Расчет размера капитала в будущем
периоде
Ответ:
Размер будущего
капитала составит 5 тыс. 308 руб. 78 коп.
Задача № 6
Рассчитайте
фондоотдачу основных фондов и определите
величину экономии капиталовложений в
результате увеличения фондоотдачи
средств, вложенных в основные фонды.
Данные для
расчета:
-
Выручка за базисный
период 100 тыс. руб. -
Среднегодовая
стоимость основных фондов за базисный
период 80 тыс. руб. -
Выручка за отчетный
период 150 тыс. руб. -
Среднегодовая
стоимость основных фондов за отчетный
период 90 тыс. руб.
Формула:
;
; ЭК
= ИФе
ВОП
Где:
ЭК
– экономия капиталовложений;
ИФе
– изменение фондоемкости;
ВОП
– выручка за отчетный период;
Фо – фондоотдача
основных фондов;
Т – объем выручки;
С – средняя
стоимость основных фондов;
Фе – фондоемкость
продукции;
100 – перевод расчета
с рубля на копейку.
Решение:
1) Расчет фондоотдачи,
фондоемкости и изменения показателей
произведем в таблице
|
Показатели |
Базисный период |
Отчетный период |
Изменения |
|
Выручка (тыс. |
100 |
150 |
+ 50 |
|
Среднегодовая |
80 |
90 |
+ 10 |
|
Фондоотдача |
1.25 |
1.67 |
+ 0.42 |
|
Фондоемкость |
80 |
60 |
– 20 |
2) Расчет экономии
капиталовложения
0.20 × 150 000 = 30 000 руб.
Ответ:
Фондоотдача
основных фондов за год возросла на 42
коп., это вызвало снижение фондоемкости
продукции на 20 коп. Повышение эффективности
использования основных фондов
способствовало экономии капиталовложений
на 30 тыс. руб.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #