Как найти первообразную для функции калькулятор онлайн - Исправление недочетов и поиск решений вместе с Examum.ru

Первообразная (неопределенный интеграл)

Ранее мы по заданной функции, руководствуясь различными формулами и правилами, находили ее производную. Производная имеет
многочисленные применения: это скорость движения (или, обобщая, скорость протекания любого процесса); угловой коэффициент касательной
к графику функции; с помощью производной можно исследовать функцию на монотонность и экстремумы; она помогает решать задачи на
оптимизацию.

Но наряду с задачей о нахождении скорости по известному закону движения встречается и обратная задача — задача о восстановлении
закона движения по известной скорости. Рассмотрим одну из таких задач.

Пример 1. По прямой движется материальная точка, скорость ее движения в момент времени t задается формулой v=gt. Найти
закон движения.
Решение. Пусть s = s(t) — искомый закон движения. Известно, что s'(t) = v(t). Значит, для решения задачи нужно подобрать функцию
s = s(t), производная которой равна gt. Нетрудно догадаться, что ( s(t) = frac{gt^2}{2} ). В самом деле
( s'(t) = left( frac{gt^2}{2} right)’ = frac{g}{2}(t^2)’ = frac{g}{2} cdot 2t = gt )
Ответ: ( s(t) = frac{gt^2}{2} )

Сразу заметим, что пример решен верно, но неполно. Мы получили ( s(t) = frac{gt^2}{2} ). На самом деле задача имеет бесконечно
много решений: любая функция вида ( s(t) = frac{gt^2}{2} + C ), где C — произвольная константа, может служить законом движения,
поскольку ( left( frac{gt^2}{2} +C right)’ = gt )

Чтобы задача стала более определенной, нам надо было зафиксировать исходную ситуацию: указать координату движущейся точки в
какой-либо момент времени, например при t = 0. Если, скажем, s(0) = s₀, то из равенства s(t) = (gt²)/2 + C
получаем: s(0) = 0 + С, т. е. C = s₀. Теперь закон движения определен однозначно: s(t) = (gt²)/2 + s₀.

В математике взаимно обратным операциям присваивают разные названия, придумывают специальные обозначения, например:
возведение в квадрат (х²) и извлечение квадратного корня ( ( sqrt{x} ) ), синус (sin x) и арксинус (arcsin x) и т. д.
Процесс нахождения производной по заданной функции называют дифференцированием, а обратную операцию, т. е. процесс нахождения
функции по заданной производной, — интегрированием.

Сам термин «производная» можно обосновать «по-житейски»: функция у = f(x) «производит на свет» новую функцию у’ = f'(x).
Функция у = f(x) выступает как бы в качестве «родителя», но математики, естественно, не называют ее «родителем» или «производителем»,
они говорят, что это, по отношению к функции у’ = f'(x), первичный образ, или первообразная.

Определение. Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке X, если для ( x in X )
выполняется равенство F'(x) = f(x)

На практике промежуток X обычно не указывают, но подразумевают (в качестве естественной области определения функции).

Приведем примеры.
1) Функция у = х² является первообразной для функции у = 2х, поскольку для любого х справедливо равенство
(x²)’ = 2х
2) Функция у = х³ является первообразной для функции у = 3х², поскольку для любого х справедливо равенство
(x³)’ = 3х²
3) Функция у = sin(x) является первообразной для функции y = cos(x), поскольку для любого x справедливо равенство
(sin(x))’ = cos(x)

При нахождении первообразных, как и производных, используются не только формулы, но и некоторые правила. Они непосредственно
связаны с соответствующими правилами вычисления производных.

Мы знаем, что производная суммы равна сумме производных. Это правило порождает соответствующее правило нахождения первообразных.

Правило 1. Первообразная суммы равна сумме первообразных.

Мы знаем, что постоянный множитель можно вынести за знак производной. Это правило порождает соответствующее правило нахождения первообразных.

Правило 2. Если F(x) — первообразная для f(x), то kF(x) — первообразная для kf(x).

Теорема 1. Если y = F(x) — первообразная для функции y = f(x), то первообразной для функции у = f(kx + m) служит функция
( y=frac{1}{k}F(kx+m) )

Теорема 2. Если y = F(x) — первообразная для функции y = f(x) на промежутке X, то у функции у = f(x) бесконечно много
первообразных, и все они имеют вид y = F(x) + C.

Методы интегрирования

Метод замены переменной (метод подстановки)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом
заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора
подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл ( textstyle int F(x)dx ). Сделаем подстановку ( x= varphi(t) ) где
( varphi(t) ) — функция, имеющая непрерывную производную.
Тогда ( dx = varphi ‘ (t) cdot dt ) и на основании свойства инвариантности формулы интегрирования неопределенного интеграла
получаем формулу интегрирования подстановкой:
( int F(x) dx = int F(varphi(t)) cdot varphi ‘ (t) dt )

Интегрирование выражений вида ( textstyle int sin^n x cos^m x dx )

Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.
Если n и m чётные, то удобнее сделать подстановку tg x = t.

Интегрирование по частям

Интегрирование по частям — применение следующей формулы для интегрирования:
( textstyle int u cdot dv = u cdot v — int v cdot du )
или:
( textstyle int u cdot v’ cdot dx = u cdot v — int v cdot u’ cdot dx )

Таблица неопределённых интегралов (первообразных) некоторых функций

$$ int 0 cdot dx = C $$

$$ int 1 cdot dx = x+C $$

$$ int x^n dx = frac{x^{n+1}}{n+1} +C ;; (n neq -1) $$

$$ int frac{1}{x} dx = ln |x| +C $$

$$ int e^x dx = e^x +C $$

$$ int a^x dx = frac{a^x}{ln a} +C ;; (a>0, ;; a neq 1) $$

$$ int cos x dx = sin x +C $$

$$ int sin x dx = -cos x +C $$

$$ int frac{dx}{cos^2 x} = text{tg} x +C $$

$$ int frac{dx}{sin^2 x} = -text{ctg} x +C $$

$$ int frac{dx}{sqrt{1-x^2}} = text{arcsin} x +C $$

$$ int frac{dx}{1+x^2} = text{arctg} x +C $$

$$ int text{ch} x dx = text{sh} x +C $$

$$ int text{sh} x dx = text{ch} x +C $$

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Показать Этапы

Номер Строки

Примеры

int xln(x)dx
int sin (2x)dx
int frac{x}{x^2+1}dx
int cos (sqrt{x})dx
int sin ^2(x)+cos ^2(x)dx
int :xe^xdx
Показать больше

Описание

Поэтапное решение первообразной функции

antiderivative-calculator

Блог-сообщения, имеющие отношение к Symbolab

Advanced Math Solutions – Integral Calculator, the complete guide

We’ve covered quite a few integration techniques, some are straightforward, some are more challenging, but finding…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Введите функцию, переменную, верхнюю и нижнюю границы. Выберите вариант с определенным или неопределенным целым. Нажмите кнопку «Рассчитать», чтобы найти интеграл с помощью первообразного калькулятора.

Онлайн-калькулятор интеграла — это инструмент, который вычисляет интеграл заданной функции по переменной. Он также вычисляет как определенный, так и неопределенный интеграл для заданной функции.

Этот калькулятор интегралов также показывает шаги интегрирования для каждого расчета.

Что такое интеграл?

Интеграл можно определить как

«Интеграл присваивает числа функциям таким образом, чтобы можно было определить объем, смещение площади и даже вероятность. Интеграл — это функция, обратная производной, поэтому его обычно называют первообразной ».

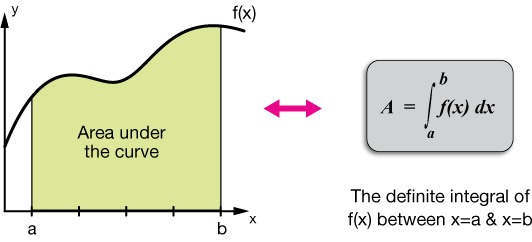
Процесс нахождения интеграла известен как интегрирование. Он используется для определения площади под кривой. Символ интеграции или первообразной — ∫.

Как оценить интеграл?

Пример: вычислите следующий интеграл.

∫ (6x + 2) dx

Решение:

Шаг 1: Примените линейность к функции.

= 6 ∫ x dx + 2 ∫ 1 dx ——- 1

Шаг 2: Решите 6 ∫ x dx и 2 ∫ 1 dx отдельно и поместите значения в уравнение (1) выше.

6 ∫ x dx

Примените правило силы.

6 ∫ х dx = 6×2 / 2 = 3×2

2 ∫ 1 дх

Примените правило константы ∫a dx = ax + C.

2 ∫ 1 dx = 2x + C

Шаг 3: Поместите решенные интегралы в уравнение (1).

= 6 ∫ x dx + 2 ∫ 1 dx

= 3×2 + 2x + C

Приведенный выше интегральный решатель выполняет все эти шаги и для вашего удобства показывает полный расчет.

Источник

Калькулятор первообразных с шагами

Калькулятор первообразной находит первообразную функции шаг за шагом по переменной, т. е. x, y или z. Этот онлайн-калькулятор интеграции также поддерживает верхнюю и нижнюю границы, если вы работаете с минимальным или максимальным значением интервалов.

С помощью этого интегрального калькулятора вы можете получить пошаговые расчеты:

Определенный интеграл
Неопределенный интеграл

Он может найти интегралы логарифмических, а также тригонометрических функций. Этот инструмент оценивает входную функцию и соответственно использует интегральные правила для вычисления интегралов для площади, объема и т. д.

Как работает антипроизводный калькулятор?

Этот инструмент использует синтаксический анализатор, который анализирует заданную функцию и преобразует ее в дерево. Компьютер интерпретирует дерево для правильной оценки порядка операций и соответствующим образом реализует правила интеграции.

Вы можете найти первообразную (интеграл) любой функции, выполнив следующие действия.

Выберите определенный или неопределенный вариант.
Введите функцию в данное поле ввода.
Нажмите кнопку «Загрузить пример», если вы хотите использовать образец примера.
Укажите переменную. По умолчанию он установлен как x.
Введите верхнюю и нижнюю границы, если вы выбрали определенный интеграл выше.
Нажмите кнопку «Рассчитать». Вы получите результат с пошаговыми расчетами.

Вы можете скачать решение, нажав на иконку.

Что такое интеграл?

Интеграл можно определить как

«Integral присваивает числа функциям таким образом, который описывает объем, площадь, перемещение и другие идеи, возникающие при объединении бесконечно малых данных».

Процесс нахождения интегралов называется интегрированием. Интеграл также называют первообразной, потому что это обратная операция вывода.

Наряду с дифференцированием интегрирование является важной операцией исчисления и служит инструментом для решения задач в математике и физике, связанных с длиной кривой, объемом твердого тела и площадью произвольной формы среди других.

Интеграл функции f(x) по действительной переменной x на интервале [a, b] записывается как:

(int _a^bfleft(xright)dx:)

Как найти первообразную (интеграл)?

См. приведенные ниже примеры, чтобы узнать, как вычислять определенные и неопределенные интегралы, используя правила интегрирования.

Пример №1

Определенный интеграл

Оценивать (int _0^1left(sqrt{x}+sqrt[3]{x}right)dx:)

Решение:

Примените правило сумм. Запишите знак интегрирования с каждой переменной отдельно.

(int _0^1sqrt{x}dx+int _0^1x^{frac{1}{3}}dx:)

Вышеупомянутая функция может быть записана как:

(=int _0^1x^{frac{1}{2}}dx+int _0^1x^{frac{1}{3}}dx:)

Примените степенное правило к обоим выражениям, чтобы вычислить показатели степени.

Правило питания: (int x^ndx=frac{x^{n+1}}{n+1}:)

(int _0^1left(sqrt{x}+sqrt[3]{x}right)dx:=left[frac{x^{frac{1}{2}+1}}{frac{1}{2}+1}right]^1_0+left[frac{x^{frac{1}{3}+1}}{frac{1}{3}+1}right]^1_0)

(int _0^1left(sqrt{x}+sqrt[3]{x}right)dx:=left[frac{x^{frac{3}{2}}}{frac{3}{2}}right]^1_0+left[frac{x^{frac{4}{3}}}{frac{4}{3}}right]^1_0)

(int _0^1left(sqrt{x}+sqrt[3]{x}right)dx:=left[frac{2x^{frac{3}{2}}}{3}right]^1_0+left[frac{3x^{frac{4}{3}}}{4}right]^1_0)

Примените постоянное правило, которое оставляет C с окончательным выражением.

Постоянное правило:

(int _0^1left(sqrt{x}+sqrt[3]{x}right)dx:=frac{2}{3}left[x^{frac{3}{2}}right]^1_0+frac{3}{4}left[x^{frac{4}{3}}right]^1_0)

(int _0^1left(sqrt{x}+sqrt[3]{x}right)dx:=frac{2}{3}left[1^{frac{3}{2}}-0^{frac{3}{2}}right]+frac{3}{4}left[1^{frac{4}{3}}-0^{frac{4}{3}}right])

(int _0^1left(sqrt{x}+sqrt[3]{x}right)dx:=frac{2}{3}left[1-0right]+frac{3}{4}left[1-0right])

(int _0^1left(sqrt{x}+sqrt[3]{x}right)dx:=frac{2}{3}+frac{3}{4})

(int _0^1left(sqrt{x}+sqrt[3]{x}right)dx:=frac{17}{12}=1.4167)

Пример №2

Неопределенный интеграл

Оценивать (int left(3x^2−6x+2sinleft(xright)right)dx)

Решение:

Переставьте функцию, как показано ниже.

(int left(2sinleft(xright)+3x^2−6xright)dx)

Примените правило сумм к функции.

Правило суммы:

(int left(f+gright)dx=int f:dx+int g:dx)

(int left(2sinleft(xright)+3x^2−6xright)dx=2int sinleft(xright)dx+3int x^2dx−6int xdx) …Уравнение 1

Решите каждое выражение в приведенной выше функции, реализуя интегральные правила.

(int sinleft(xright)dx=-cosleft(xright)) … d/dx sin(x)=cos(x)

(int x^2dx=frac{x^3}{3}:)

(int xdx=frac{x^2}{2}:)

Подставьте значения решения в уравнение 1.

(int :left(2sinleft(xright)+3x^2−6xright)dx=-2cosleft(xright)+frac{3x^3}{3}−frac{6x^2}{2}+C)

C добавлен из-за постоянного правила.

Упростите уравнение, если это необходимо.

(int :left(2sinleft(xright)+3x^2−6xright)dx=-2cosleft(xright)+x^3−3x^2+C)

Часто задаваемые вопросы

Чему равен интеграл от 1/x?

Интеграл от 1/x представляет собой абсолютное значение: ln (|x|) + C. Это стандартное значение интегрирования.

Чем отличается определенный интеграл от неопределенного?

Определенный интеграл обозначает число, когда верхняя и нижняя границы являются постоянными. С другой стороны, неопределенный интеграл – это семейство функций, производная которых равна f. Разница между двумя функциями является константой.

Что такое первообразная tan(x) dx?

Первообразная tan(x) dx равна,

тангенс x = — ln |cos x| + С

Источник

Онлайн-калькулятор интегралов поможет вам вычислить интегралы функций по отношению к задействованной переменной и покажет вам полные пошаговые вычисления. Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет мгновенно решать неопределенные интегралы. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-интеграл калькулятор:

Определенные интегралы
Неопределенные интегралы (первообразная)

Интегральный расчет довольно сложно решить вручную, так как он включает в себя различные сложные формулы интегрирования. Итак, рассмотрим интерактивный интегральный решатель, который решает простые и сложные функции решение интегралов онлайн и показывает вам пошаговые вычисления.

Итак, сейчас самое время понять формулы интегрирования, как интегрировать функцию шаг за шагом, с помощью калькулятора интегрирования и многое другое. Во-первых, давайте начнем с основ:

Читать дальше!

Что такое интеграл?

В математике интеграл функций описывает площадь, смещение, объем и другие понятия, которые возникают, когда мы объединяем бесконечные данные. В исчислении дифференцирование и интегрирование являются фундаментальной операцией и служат наилучшей операцией для решения физико-математических задач произвольной формы.

Вы также можете использовать бесплатную версию онлайн-калькулятора факторов, чтобы найти факторы, а также пары факторов для положительных или отрицательных целых чисел.

Процесс нахождения интегралов, называемый интегрированием
Интегрируемая функция называется подынтегральной функцией.
В интегральных обозначениях ∫3xdx, ∫ – символ интеграла, 3x – интегрируемая функция, а dx – дифференциал переменной x.

Где f (x) – функция, а A – площадь под кривой. Наш бесплатный калькулятор интегралов легко вычисляет интегралы и определяет площадь под заданной функцией. Что ж, теперь поговорим о типах интегралов:

Типы интегралов:

По сути, есть два типа интегралов:

Неопределенные интегралы
Определенные интегралы

Неопределенные интегралы:

определенный интеграл онлайн функции принимает первообразную другой функции. Взять первообразную функции – это самый простой способ обозначить неопределенные интегралы. Когда дело доходит до вычисления неопределенных интегралов, калькулятор неопределенных интегралов помогает выполнять вычисления неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет верхнего или нижнего предела.

Определенные интегралы:

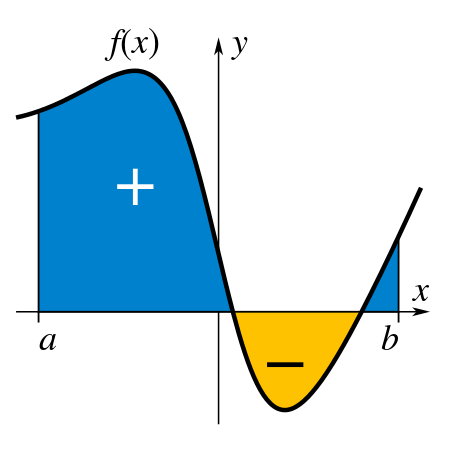
Определенный интеграл функции имеет начальное и конечное значения. Просто существует интервал [a, b], который называется пределами, границами или границами. Этот тип можно определить как предел интегральных сумм, когда диаметр разбиения стремится к нулю. Наш интеграл онлайн калькулятор определенных интегралов с оценками вычисляет интегралы, учитывая верхний и нижний предел функции. Разницу между определенным и неопределенным интегралами можно понять по следующей диаграмме:

Основные формулы для интеграции:

Существуют разные формулы для интеграции, но здесь мы перечислили некоторые общие:

∫1 dx = x + c
∫xn dx = xn + 1 / n + 1 + c
∫a dx = ax + c
∫ (1 / х) dx = lnx + c
∫ ax dx = ax / lna + c
∫ ex dx = ex + c
∫ sinx dx = -cosx + c
∫ cosx dx = sinx + c
∫ tanx dx = – ln | cos x | + c
∫ cosec2x dx = – детская кроватка x + c
∫ sec2x dx = tan x + c
∫ cotx dx = ln | sinx | + c
∫ (secx) (tanx) dx = secx + c
∫ (cosecx) (cotx) dx = -cosecx + c

Помимо этих уравнений интегрирования, есть еще несколько важных формул интегрирования, которые упомянуты ниже:

∫ 1 / (1-x2) 1/2 dx = sin-1x + c
∫ 1 / (1 + x2) 1/2 dx = cos-1x + c
∫ 1 / (1 + x2) dx = tan-1x + c
∫ 1 / | x | (x2 – 1) 1/2 dx = cos-1x + c

Запоминание всех этих формул интегрирования и выполнение вычислений вручную – очень сложная задача. Просто введите функцию в предназначенное для этого поле онлайн-калькулятор интегралов, который использует эти стандартизированные формулы для точных вычислений.

Как решать интегралы вручную (шаг за шагом):

Большинство людей раздражается начинать с вычислений интегральной функции. Но здесь мы собираемся решать интегральные примеры шаг за шагом, что поможет вам разобраться, как легко интегрировать функции! Итак, это точки, которым нужно следовать для вычисления решение интегралов онлайн:

Определить функцию f (x)
Возьмите первообразную функции
Вычислить верхний и нижний предел функции
Определите разницу между обоими пределами

Если вас интересует вычисление первообразной (неопределенного интеграла), тогда возьмите онлайн-калькулятор первообразной, который быстро решит первообразную данной функции.

Смотрит на примеры:

Пример 1:

Решить интегралы от ∫ x3 + 5x + 6 dx?

Решение:

Шаг 1:

Применяя правило функциональной мощности для интегрирования:

∫xn dx = xn + 1 / n + 1 + c

∫ x3 + 5x + 6 dx = x3 + 1/3 + 1 + 5 x1 + 1/1 + 1 + 6x + c

Шаг 2:

∫ x3 + 5x + 6 dx = x4 / 4 + 5 x2 / 2 + 6x + c

Шаг 3:

∫ x3 + 5x + 6 dx = x4 + 10×2 + 24x / 4 + c

Этот калькулятор неопределенного интеграла помогает интегрировать интеграл калькулятор функции шаг за шагом, используя формулу интегрирования.

Пример 2 (Интеграл логарифмической функции):

Вычислить ∫ ^ 1_5 xlnx dx?

Решение:

Шаг 1:

Прежде всего, разместите функции согласно правилу ILATE:

∫ ^ 1_5 lnx * x dx

Шаг 2:

Теперь используя формулу для интегрирования по частям i; e:

∫u.v dx = u∫vdx – ∫ [∫vdx d / dx u]

Шаг 3:

∫ ^ 1_5 x * lnx dx = [lnx∫xdx – ∫ [∫xdx d / dx lnx]] ^ 1_5

∫ ^ 1_5 x * lnx dx = [lnx x2 / 2 – ∫ [x2 / 2 1 / x]] ^ 1_5

∫ ^ 1_5 x * lnx dx = [lnx x2 / 2 – ∫ [x / 2]] ^ 1_5

∫ ^ 1_5 x * lnx dx = [lnx x2 / 2 – 1 / 2∫ x] ^ 1_5

∫ ^ 1_5 x * lnx dx = [lnx x2 / 2 – 1/2 x2 / 2] ^ 1_5

∫ ^ 1_5 x * lnx dx = [lnx x2 / 2 – 1/4 x2] ^ 1_5

∫ ^ 1_5 x * lnx dx = [ln1 (1) 2/2 – 1/4 (1) 2] – [ln5 (5) 2/2 – 1/4 (5) 2]

∫ ^ 1_5 x * lnx dx = [0 (0) / 2 – 1/4 (1)] – [1,60 (25) / 2 – 1/4 (25)]

∫ ^ 1_5 x * lnx dx = [0 – 1/4] – [40/2 – 25/4]

∫ ^ 1_5 x * lnx dx = [- 1/4] – [20 – 6.25]

∫ ^ 1_5 x * lnx dx = – 0,25 – 13,75

∫ ^ 1_5 x * lnx dx = –14

Поскольку это очень сложно для решения интегралов, когда две функции умножаются друг на друга. Для удобства просто введите функции в онлайн-калькулятор интегралов по частям, который помогает выполнять вычисления двух функций (по частям), которые точно умножаются друг на друга.

Пример 3 (Интеграл от тригонометрической функции):

Вычислить определенный интеграл для ∫sinx dx с интервалом [0, π / 2]?

Решение:

Шаг 1:

Используйте формулу для тригонометрической функции:

∫ sinx dx = -cosx + c

Шаг 2:

Вычислите верхний и нижний предел для функций f (a) и f (b) соответственно:

Поскольку a = 0 и b = π / 2

Итак, f (a) = f (0) = cos (0) = 1

f (b) = f (π / 2) = cos (π / 2) = 0

Шаг 3:

Рассчитайте разницу между верхним и нижним пределами:

f (а) – f (b) = 1 – 0

f (а) – f (b) = 1

Теперь вы можете использовать бесплатный калькулятор частичных интегралов для проверки всех этих примеров и просто добавлять значения в поля назначения для мгновенного вычисления интегралов.

Как найти первообразную и вычислить интегралы с помощью калькулятора интегралов:

Вы можете легко вычислить интеграл от определенных и неопределенных функций с помощью лучшего интегратора. Вам просто нужно следовать указанным пунктам, чтобы получить точные результаты:

Проведите по!

Входы:

Во-первых, введите уравнение, которое вы хотите интегрировать.
Затем выберите зависимую переменную, входящую в уравнение
Выберите на вкладке определенный или определенный интеграл онлайн
Если вы выбрали конкретный вариант, то вам следует ввести нижнюю и верхнюю границу или предел в предназначенное для этого поле.
После этого пора нажать на кнопку расчета.

Выходы:

Интегральный оценщик показывает:

Определенный интеграл
неопределенный интеграл онлайн
Выполните пошаговые расчеты

Часто задаваемые вопросы (FAQ):

Какое целое значение?

В математике интеграл – это числовое значение, равное площади под графиком некоторой функции на некотором интервале. Это может быть график новой функции, производная которой является исходной функцией (калькулятор неопределенных интегралов). Итак, для мгновенных и быстрых вычислений вы можете использовать бесплатный интеграл онлайн калькулятор первообразных, который позволяет вам решать неопределенные интегральные функции.

Как вы оцениваете интеграл, используя основную теорему исчисления?

Прежде всего, мы должны найти первообразную функции, чтобы решить интеграл, используя фундаментальную теорему. Затем используйте основную теорему исчисления для вычисления решение интегралов онлайн. Или просто введите значения в предназначенное для этого поле этого калькулятора интеграции и мгновенно получите результаты.

Что такое двойной интеграл?

Двойные интегралы – это способ интегрирования по двумерной области. Двойные интегралы позволяют вычислить объем поверхности под кривой. Они имеют две переменные и рассматривают функцию f (x, y) в трехмерном пространстве.

Заключительные слова:

Интегралы широко используются для улучшения архитектуры зданий, а также для мостов. В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся на расстоянии нескольких миль друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для школьного образования, который легко интеграл калькулятор любой заданной функции шаг за шагом.

Other Languages: Integral Calculator, Integral Hesaplama, Kalkulator Integral, Kalkulator Integralny, Integralrechner, 積分計算, 적분계산기, Integrály Kalkulačka, Calculadora De Integral, Calcul Intégrale En Ligne, Calculadora De Integrales, Calcolatore Integrali, حساب متكامل, Integraatio Laskin, Integreret Lommeregner, Integral Kalkulator, Integralni Kalkulator, เครื่องคำนวณอินทิกรัล, Integrale Rekenmachine.

Источник