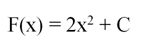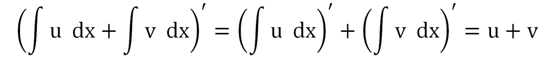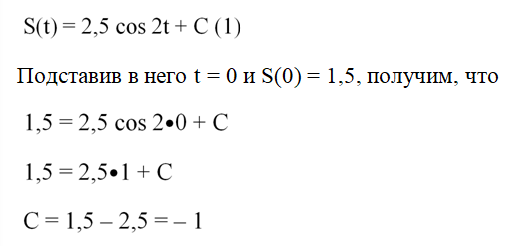Как найти первообразную функции синус

План урока:

Понятие первообразной

Бесконечное количество первообразных

Неопределенный интеграл

Таблица первообразных

Правила вычисления интегралов

Физический смысл неопределенного интеграла

Понятие первообразной

Ранее мы познакомились с важнейшим понятием математического анализа – производной. Она имеет большое практическое значение, в частности, с ее помощью можно определить скорость тела, если известен закон его передвижения. Например, если путь, пройденный автомобилем, можно вычислить с помощью функции S = t², то его скорость в любой момент времени может быть рассчитана по формуле

Однако на практике значительно чаще встречается прямо противоположная задача. Известно, как меняется скорость тела, и найти требуется путь, пройденный им. В таком случае необходимо по производной определить ту функцию, которая «подверглась» дифференцированию.

Задание. Известна производная функции у(х):

В этом примере мы выполнили операцию, обратную дифференцированию. В математическом анализе он называется интегрированием. Если интегрируют некоторую произвольную функцию f(х), то в итоге получают новую функцию, которую чаще всего обозначают как F(x). Её называют первообразной функции f(x).

Приведем несколько примеров первообразной:

Последний пример показывает, что иногда первообразная может и совпадать с исходной функцией.

Задание. Докажите, что функция

Первообразные встречаются и в ряде практических задач, особенно в тех, где рассматривается движение тел.

Задание. Автомобиль Buggati Veyron разгоняется от 0 до 40 м/с за 4 секунды. Какое расстояние проедет эта машина за эти 4 секунды, если разгон осуществляется равномерно?

Решение: Если за 4 секунды машина разгоняется до 30 м/с, то за одну секунду она увеличивает скорость на

Примечание – в будущем мы научимся более строго решать такие задачи, и «угадывать» подходящую первообразную не придётся.

Бесконечное количество первообразных

Рассмотрим функцию

Оказывается, что g₁ также является первообразной для у. То есть у одной функции у = 4х³ есть сразу две первообразных:g = x⁴и g = x⁴ + 1! Более того, можно доказать, что у любой функции есть бесконечное количество первообразных!

Действительно, рассмотрим сразу все функции

где С – некоторая константа, то есть параметр. В данном случае можно сказать, что мы рассматриваем не одну функцию, а семейство функций. Продифференцируем g:

Мы видим, что у всех функций из этого семейства, независимо от значения параметра С, производная одинакова. Здесь С может принимать любое действительное значение. Так как действительных чисел бесконечно много, то и количество функций, образующих семейство, также бесконечно. И все они являются первообразными для у = 4х³.

Данная особенность операции интегрирования может быть сформулирована в виде следующей теоремы:

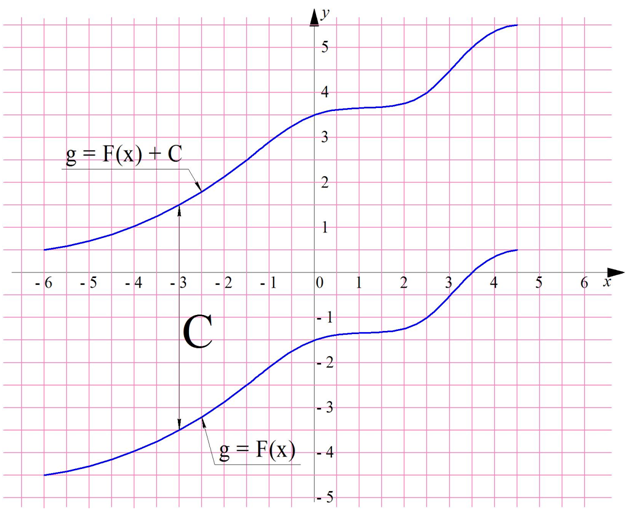
Можно дать и графическую иллюстрацию этого правила. Построим произвольный график g = F(x). Далее построим ещё один график

Очевидно, что он может быть получен параллельным переносом первого графика на С единиц вверх:

Теперь в какой-нибудь точке х₀ проведем касательные к обоим графикам первообразных. Очевидно, что они будут иметь одинаковый угол наклона, так как по сути тоже могут быть получены параллельным переносом:

Если же углы наклона касательных совпадают, то и производные в этих точках также равны.

В связи с наличием у каждой функции бесконечного количества первообразных их часто записывают в общем виде. Например, пусть надо записать первообразную для

Однако 2х² – это лишь одна из бесконечного множества первообразных. Все вместе они образуют семейство, которое записывается так:

Неопределенный интеграл

Каждая математическая операция имеет какое-то особое обозначение. Например, чтобы показать, что мы дифференцируем некоторую функцию, мы ставим после неё штрих (и при необходимости берем в скобки):

Напомним, что операция нахождения первообразной называется интегрированием. Для ее обозначения используется особый знак – интеграл. Например, мы знаем, что первообразная для у = х² – это семейство функций вида

Рассмотрим элементы записанного нами равенства:

Исходная функция – это та самая функция, для которой необходимо найти первообразную, то есть интегрируемая функция. Справа от знака «равно» как раз записывается первообразная. Сразу после первообразной надо писать «+ С». Тем самым мы показываем, что у интегрируемой функции есть бесконечное количество первообразных.

После интегрируемой функции стоит так называемый дифференциал dх (читается как «дэ икс»). В данном случае он указывает, что именно буквой х мы обозначаем переменную в интегрируемой функции. Его значение мы разберем несколько позже. Пока что надо запомнить, что после интегрируемой функции необходимо писать «dx». В целом вся запись

читается так: «интеграл от два икс по дэ икс равен икс в квадрате плюс цэ».

В чем разница между первообразной и интегралом? Первообразная – это функция, при дифференцировании которой получается исходная функция. Интеграл же – это не функция, а целое семейство функций (или их множество), которое включает в себя сразу все первообразные интегрируемой функции.

Так как интегрирование – это действие, обратное дифференцированию, то мы можем проверить результат своих вычислений. Пусть мы записали, что

Получили подынтегральное выражение. Значит, мы всё сделали правильно.

Здесь важно заметить, что в математике существует сразу несколько видов интегралов, каждый из которых имеет разное определение. Здесь описан так называемый «неопределенный интеграл». Несложно догадаться, что существует ещё и «определенный интеграл», который мы рассмотрим на следующих уроках. Теперь можно дать следующее определение:

Задание. Найдите неопределенный интеграл

Решение. Вспомним таблицу производных элементарных функций. Производная синуса равна косинусу:

Заметим, что непосредственно из определения следует важное свойство неопределенного интеграла – производная интеграла равна его подынтегральному выражению:

Грубо говоря, операции интегрирования дифференцирования «сокращают» друг друга.

Задание. Вычислите производную:

Таблица первообразных

Как же вычислять интегралы? Проще всего начать с тех функций, которые уже есть в таблице производных. Напомним, как она выглядит:

Из определения первообразной следует, что для тех функций, которые указаны во втором столбце таблицы, одной из первообразных является соответствующая функция из первого столбца. То есть можно составить такую таблицу первообразных:

Обратите внимание на третью строку снизу. Здесь произошло небольшое изменение – вместо первообразной lnx мы записали ln |x|, то есть использовали модуль числа. Дело в том, что функция

определена при любом значении аргумента, кроме нуля. В то же время функция

не определена при отрицательных значениях х, так как под знаком логарифма не может стоять отрицательное число. Однако области определения интегрируемой функции и ее первообразной должны совпадать. Использование модуля обеспечивает выполнение этого условия.

Полученная нами таблица интегралов не совсем удобна. Предположим, нам надо проинтегрировать функцию

отличающуюся от интересующей нас функции лишь множителем перед х⁵.

Однако можно догадаться, что в качестве подходящей первообразной можно взять функцию

В связи с этим есть смысл немного подкорректировать таблицу первообразных таким образом, чтобы в первом столбце стояли стандартные функции без неудобных множителей. В результате таблица примет следующий вид:

Можно доказать, что каждое равенство в третьем столбце является справедливым. Возьмем, например, равенство

Получили подынтегральное выражение, а это значит, что равенство справедливо. Таким же образом можно доказать и все остальные равенства в таблице.

Задание. Вычислите неопределенный интеграл:

Решение. Этот интеграл присутствует в таблице (7-ая строка), а потому мы просто переписываем равенство из неё:

Задание. Найдите первообразную функции

Правила вычисления интегралов

Что делать в том случае, если надо вычислить интеграл, которого нет в таблице? Существует три несложных правила интегрирования, которые могут помочь в такой ситуации.

Докажем это правило. Для этого просто продифференцируем правую часть равенства:

Получили именно то выражение, которое стоит под знаком интеграла в левой части равенства. Это значит, что формула справедлива.

Рассмотрим пример использования этого правила. Пусть надо найти первообразную функции

Здесь мы представили исходный интеграл как сумму двух более простых интегралов, которые являются табличными

Обратите внимание, что мы не стали складывать константы интегрирования С как подобные слагаемые и писать 2С. Дело в том, что С – это некоторое произвольное число. Но если сложить два произвольных числа, то в итоге получится третье произвольное число, которое также будет обозначаться как С! Поэтому обычно константу С просто дописывают в самом конце решаемого примера.

Естественно, что правило сложения интегралов работает и в случае суммы не двух, а большего количества слагаемых.

Задание. Вычислите неопределенный интеграл

Возможна ситуация, когда мы не уверены в правильности полученного решения. В таком случае можно легко проверить себя, просто продифференцировав получившийся интеграл. В итоге мы должны получить исходную функцию (подынтегральное выражение):

Следующее правило позволяет выносить множитель из-под знака интеграла.

Для доказательства тождества снова продифференцируем его левую часть:

Получили как раз то выражение, которое стоит под интегралом справа. Следовательно, формула верна.

Рассмотрим несколько простейших примеров использования этого метода интегрирования неопределенных интегралов:

Естественно, что правила 1 и 2 можно комбинировать друг с другом, решая более сложные примеры.

Задание. Вычислите неопределенный интеграл от квадратичной функции

Первые два правила достаточно просты и напоминают аналогичные правила дифференцирования. А вот третий метод вычисления неопределенного интеграла более сложный.

Проиллюстрируем его на примере. Пусть надо найти первообразную для функции

Но в нашем случае под знаком косинуса стоит не х, а выражение 5х + 7, являющееся линейной функцией. Поэтому, согласно правилу, мы должны написать впервообразной не sinx, а sin (5x + 7), то есть изменить аргумент. Также надо добавить перед синусом «поправочный множитель», равный 1/k, то есть в нашем случае 1/5:

Проверим себя. Продифференцируем получившуюся первообразную. При этом мы используем правило дифференцирования сложной функции:

Получили ту самую функцию, которую и надо было проинтегрировать.

Приведем ещё несколько примеров использования правила 3:

Напомним, что при изучении производной мы познакомились также с правилами дифференцирования произведения, дроби и сложной функции. Используя их, мы могли найти производную для почти любой функции, которую только могли записать. С решением неопределенных интегралов ситуация значительно сложнее. С помощью приведенных трех правил не получится вычислить такие интегралы, как

Более того, в записанной нами таблице интегралов отсутствует ряд элементарных функций, поэтому мы не сможем даже проинтегрировать такую простую функцию, как

Дело в том, что задача интегрирования является значительно более сложной, чем задача дифференцирования. Отметим три момента. Во-первых, в нашей школьной таблице интегралов, содержащей всего 11 формул, указаны лишь самые простые элементарные функции. Существуют справочники, где в качестве табличных указаны интегралы десятков, а то и сотен функций. Во-вторых, есть и более сложные правила интегрирования, которые изучаются уже в институте. В-третьих, существуют такие элементарные функции, первообразную которых в принципе невозможно записать, используя элементарные функции (синус, косинус, логарифм и т.п.). В связи с этим приходится вводить в рассмотрение новые специальные функции, а также использовать приближенные методы вычислений.

Физический смысл неопределенного интеграла

Напомним физический смысл производной – если известен закон движения материальной точки, то есть некоторая функция S(t), то производная этого закона будет выражать скорость тела в момент времени t:

Отсюда прямо вытекает физический смысл первообразной. Если известен закон изменения скорости v(t), то его первообразная будет являться законом движения S(t). Точнее говоря, законом движения будет являться только одна из первообразных, так как их существует бесконечно много.

Задача. Скорость тела в произвольный момент времени t может быть вычислена по закону

Найдите закон движения материальной точки S(t). Известно, что в начальный момент времени тело находилось в точке с координатой 1,5, то есть S(0) = 1,5.

Решение. Нам надо просто проинтегрировать функцию v(t):

Интеграл вычислен, но это ещё не закон движения, ведь в нем присутствует константа интегрирования. Как от неё избавиться? Надо использовать условие, согласно которому S(0) = 1,5. В общем виде закон движения имеет вид

Мы нашли конкретное значение константы интегрирования. С учетом этого закон движения (1) примет вид:

Первообразная функции и общий вид

20 июля 2015

Этот урок — первый из серии видео, посвященных интегрированию. В нём мы разберём, что такое первообразная функции, а также изучим элементарные приёмы вычисления этих самых первообразных.

На самом деле здесь нет ничего сложного: по существу всё сводится к понятию производной, с которым вы уже должны знакомы.:)

Сразу отмечу, что, поскольку это самый первый урок в нашей новой теме, сегодня не будет никаких сложных вычислений и формул, но то, что мы изучим сегодня, ляжет в основу гораздо более сложных выкладок и конструкций при вычислении сложных интегралов и площадей.

Кроме того, приступая к изучению интегрирования и интегралов в частности, мы неявно предполагаем, что ученик уже, как минимум, знаком к понятиям производной и имеет хотя бы элементарные навыки их вычисления. Без четкого понимания этого, делать в интегрировании совершенно нечего.

Однако здесь же кроется одна из самых частых и коварных проблем. Дело в том, что, начиная вычислять свои первые первообразные, многие ученики путают их с производными. В результате на экзаменах и самостоятельных работах допускаются глупые и обидные ошибки.

Поэтому сейчас я не буду давать четкого определения первообразной. А взамен предлагаю вам посмотреть, как она считается на простом конкретном примере.

Что такое первообразная и как она считается

Допустим, нам необходимо посчитать следующую производную:

[fleft( x right)={{x}^{3}}]

Мы знаем такую формулу:

[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]

Считается эта производная элементарно:

[{f}’left( x right)={{left( {{x}^{3}} right)}^{prime }}=3{{x}^{2}}]

Посмотрим внимательно на полученное выражение и выразим ${{x}^{2}}$:

[{{x}^{2}}=frac{{{left( {{x}^{3}} right)}^{prime }}}{3}]

Но мы можем записать и так, согласно определению производной:

[{{x}^{2}}={{left( frac{{{x}^{3}}}{3} right)}^{prime }}]

А теперь внимание: то, что мы только что записали и есть определением первообразной. Но, чтобы записать ее правильно, нужно написать следующее:

[{{x}^{2}}to frac{{{x}^{3}}}{3}]

Аналогично запишем и такое выражение:

[{{x}^{4}}to frac{{{x}^{5}}}{5}]

Если мы обобщим это правило, то сможем вывести такую формулу:

[{{x}^{n}}to frac{{{x}^{n+1}}}{n+1}]

Теперь мы можем сформулировать четкое определение.

Первообразной функции называется такая функция, производная которой равна исходной функции.

Вопросы о первообразной функции

Казалось бы, довольно простое и понятное определение. Однако, услышав его, у внимательного ученика сразу возникнет несколько вопросов:

1. Допустим, хорошо, эта формула верна. Однако в этом случае при $n=1$ у нас возникают проблемы: в знаменателе появляется «ноль», а на «ноль» делить нельзя.
2. Формула ограничивается только степенями. Как считать первообразную, например, синуса, косинуса и любой другой тригонометрии, а также констант.
3. Экзистенциальный вопрос: а всегда ли вообще можно найти первообразную? Если да, то как быть с первообразной суммы, разности, произведения и т.д.?

На последний вопрос я отвечу сразу. К сожалению, первообразная, в отличие от производной, считается не всегда. Нет такой универсальной формулы, по которой из любой исходной конструкции мы получим функцию, которая будет равна этой сходной конструкции. А что касается степеней и констант — сейчас мы об этом поговорим.

Решение задач со степенными функциями

Давайте попробуем посчитать такое выражение:

[{{x}^{-1}}to frac{{{x}^{-1+1}}}{-1+1}=frac{1}{0}]

Как видим, данная формула для ${{x}^{-1}}$ не работает. Возникает вопрос: а что тогда работает? Неужели мы не можем посчитать ${{x}^{-1}}$? Конечно, можем. Только давайте для начала вспомним такое:

[{{x}^{-1}}=frac{1}{x}]

Теперь подумаем: производная какой функции равна $frac{1}{x}$. Очевидно, что любой ученик, который хоть немного занимался этой темой, вспомнит, что этому выражению равна производная натурального логарифма:

[{{left( ln x right)}^{prime }}=frac{1}{x}]

Поэтому мы с уверенностью можем записать следующее:

[frac{1}{x}={{x}^{-1}}to ln x]

Эту формулу нужно знать, точно так же, как и производную степенной функции.

Итак, что нам известно на данный момент:

• Для степенной функции — ${{x}^{n}}to frac{{{x}^{n+1}}}{n+1}$
• Для константы — $=constto cdot x$
• Частный случай степенной функции — $frac{1}{x}to ln x$

Идем далее. Что нам еще может потребоваться? Конечно же, правило вычисления первообразных от суммы и от разности. Запишем так:

[fleft( x right)to Fleft( x right)]

[gleft( x right)to Gleft( x right)]

[f+gto F+G]

[f-g=F-G]

[ccdot fto ccdot Fleft( c=const right)]

А если простейшие функции мы начнем умножать и делить, как тогда посчитать первообразную произведения или частного. К сожалению, аналогии с производной произведения или частного здесь не работают. Какой-либо стандартной формулы не существует. Для некоторых случаев существуют хитрые специальные формулы — с ними мы познакомимся на будущих видеоуроках.

Однако запомните: общей формулы, аналогичной формуле для вычисления производной частного и произведения, не существует.

Решение реальных задач

Задача № 1

[fleft( x right)={{x}^{2}}+5{{x}^{4}}]

Давайте каждую из степенных функций посчитаем отдельно:

[{{x}^{2}}to frac{{{x}^{3}}}{3}]

[5{{x}^{4}}to 5cdot frac{{{x}^{5}}}{5}={{x}^{5}}]

Возвращаясь к нашему выражению, мы запишем общую конструкцию:

[Fleft( x right)=frac{{{x}^{3}}}{3}+{{x}^{5}}]

Задача № 2

[fleft( x right)=frac{x+1}{x}]

Как я уже говорил, первообразные произведений и частного «напролом» не считаются. Однако здесь можно поступить следующим образом:

[fleft( x right)=frac{x}{x}+frac{1}{x}=1+frac{1}{x}]

Мы разбили дробь на сумму двух дробей.

Посчитаем:

[Fleft( x right)=1cdot x+ln x]

[Fleft( x right)=x+ln x]

Хорошая новость состоит в том, что зная формулы вычисления первообразных, вы уже способны считать более сложные конструкции. Однако давайте пойдем дальше и расширим наши знания еще чуть-чуть. Дело в том, что многие конструкции и выражения, которые, на первый взгляд, не имеют никакого отношения к ${{x}^{n}}$, могут быть представлены в виде степени с рациональным показателем, а именно:

[sqrt{x}={{x}^{frac{1}{2}}}]

[sqrt[n]{x}={{x}^{frac{1}{n}}}]

[frac{1}{{{x}^{n}}}={{x}^{-n}}]

Все эти приемы можно и нужно комбинировать. Степенные выражения можно

• умножать (степени складываются);
• делить (степени вычитаются);
• умножать на константу;
• и т.д.

Решение выражений со степенью с рациональным показателем

Пример № 1

[fleft( x right)=7sqrt{x}+sqrt[4]{x}]

Посчитаем каждый корень отдельно:

[]

[sqrt{x}={{x}^{frac{1}{2}}}to frac{{{x}^{frac{1}{2}+1}}}{frac{1}{2}+1}=frac{{{x}^{frac{3}{2}}}}{frac{3}{2}}=frac{2cdot {{x}^{frac{3}{2}}}}{3}]

[sqrt[4]{x}={{x}^{frac{1}{4}}}to frac{{{x}^{frac{1}{4}}}}{frac{1}{4}+1}=frac{{{x}^{frac{5}{4}}}}{frac{5}{4}}=frac{4cdot {{x}^{frac{5}{4}}}}{5}]

Итого всю нашу конструкцию можно записать следующим образом:

[Fleft( x right)=7cdot frac{2cdot {{x}^{frac{3}{2}}}}{3}+frac{5cdot {{x}^{frac{5}{4}}}}{4}=frac{14cdot {{x}^{frac{3}{2}}}}{3}+frac{4cdot {{x}^{frac{5}{4}}}}{5}]

Пример № 2

[fleft( x right)=frac{1}{sqrt{x}}-frac{1}{{{x}^{3}}}]

Запишем:

[frac{1}{sqrt{x}}={{left( sqrt{x} right)}^{-1}}={{left( {{x}^{frac{1}{2}}} right)}^{-1}}={{x}^{-frac{1}{2}}}]

Следовательно, мы получим:

[Fleft( x right)=frac{{{x}^{-frac{1}{2}+1}}}{-frac{1}{2}+1}=frac{{{x}^{frac{1}{2}}}}{frac{1}{2}}=2{{x}^{frac{1}{2}}}=2sqrt{x}]

[frac{1}{{{x}^{3}}}={{x}^{-3}}to frac{{{x}^{-3+1}}}{-3+1}=frac{{{x}^{-2}}}{-2}=-frac{1}{2{{x}^{2}}}]

Итого, собирая все в одно выражение, можно записать:

[Fleft( x right)=2sqrt{x}+frac{1}{2{{x}^{2}}}]

Пример № 3

[fleft( x right)=sqrt[4]{x}-xsqrt{x}+1]

Для начала заметим, что $sqrt[4]{x}$ мы уже считали:

[sqrt[4]{x}to frac{4{{x}^{frac{5}{4}}}}{5}]

[xsqrt{x}={{x}^{1}}cdot {{x}^{frac{1}{2}}}={{x}^{frac{3}{2}}}]

[{{x}^{frac{3}{2}}}to frac{{{x}^{frac{3}{2}+1}}}{frac{3}{2}+1}=frac{2cdot {{x}^{frac{5}{2}}}}{5}]

[1to x]

Перепишем:

[Fleft( x right)=frac{4{{x}^{frac{5}{4}}}}{5}-frac{2{{x}^{frac{5}{2}}}}{5}+x]

Надеюсь, я никого не удивлю, если скажу, что то, что мы только что изучали — это лишь самые простые вычисления первообразных, самые элементарные конструкции. Давайте сейчас рассмотрим чуть более сложные примеры, в которых помимо табличных первообразных еще потребуется вспомнить школьную программу, а именно, формулы сокращенного умножения.

Решение более сложных примеров

Задача № 1

[fleft( x right)={{left( sqrt[3]{x}-2 right)}^{2}}]

Вспомним формулу квадрата разности:

[{{left( a-b right)}^{2}}={{a}^{2}}-ab+{{b}^{2}}]

Давайте перепишем нашу функцию:

[fleft( x right)=left( sqrt[3]{x} right)-2cdot sqrt[3]{x}cdot 2+4]

[fleft( x right)={{x}^{frac{2}{3}}}-4{{x}^{frac{1}{3}}}+4]

Первообразную такой функции нам сейчас предстоит найти:

[{{x}^{frac{2}{3}}}to frac{3cdot {{x}^{frac{5}{3}}}}{5}]

[{{x}^{frac{1}{3}}}to frac{3cdot {{x}^{frac{4}{3}}}}{4}]

[4to 4x]

Собираем все в общую конструкцию:

[Fleft( x right)=frac{3{{x}^{frac{5}{3}}}}{5}-3{{x}^{frac{4}{3}}}+4x]

Задача № 2

[fleft( x right)={{left( frac{1}{x}-2 right)}^{3}}]

В этом случае нам нужно раскрыть куб разности. Вспомним:

[{{left( a-b right)}^{3}}={{a}^{3}}-3{{a}^{2}}cdot b+3acdot {{b}^{2}}-{{b}^{3}}]

С учетом этого факта можно записать так:

[fleft( x right)=frac{1}{{{x}^{3}}}-3cdot frac{1}{{{x}^{2}}}cdot 2+3cdot frac{1}{x}cdot 4-8]

Давайте немного преобразуем нашу функцию:

[fleft( x right)={{x}^{-3}}-6{{x}^{-2}}+12cdot {{x}^{-1}}-8]

Считаем как всегда — по каждому слагаемому отдельно:

[{{x}^{-3}}to frac{{{x}^{-2}}}{-2}]

[{{x}^{-2}}to frac{{{x}^{-1}}}{-1}]

[{{x}^{-1}}to ln x]

[8to 8x]

Запишем полученную конструкцию:

[Fleft( x right)=-frac{1}{2{{x}^{2}}}+frac{6}{x}+12ln x-8x]

Задача № 3

[fleft( x right)=frac{{{left( x+sqrt{x} right)}^{2}}}{x}]

Сверху у нас стоит квадрат суммы, давайте его раскроем:

[frac{{{left( x+sqrt{x} right)}^{2}}}{x}=frac{{{x}^{2}}+2xcdot sqrt{x}+{{left( sqrt{x} right)}^{2}}}{x}=]

[=frac{{{x}^{2}}}{x}+frac{2xsqrt{x}}{x}+frac{x}{x}=x+2{{x}^{frac{1}{2}}}+1]

Далее все легко:

[xto frac{{{x}^{2}}}{2}]

[{{x}^{frac{1}{2}}}to frac{2cdot {{x}^{frac{3}{2}}}}{3}]

[1to x]

Давайте напишем итоговое решение:

[Fleft( x right)=frac{{{x}^{2}}}{x}+frac{4{{x}^{frac{3}{2}}}}{3}+x]

А теперь внимание! Очень важная вещь, с которой связана львиная доля ошибок и недопониманий. Дело в том, что до сих пор считая первообразные с помощью производных, приводя преобразования, мы не задумывались о том, чему равна производная константы. А ведь производная константы равна «нулю». А это означает, что можно записать такие варианты:

1. ${{x}^{2}}to frac{{{x}^{3}}}{3}$
2. ${{x}^{2}}to frac{{{x}^{3}}}{3}+1$
3. ${{x}^{2}}to frac{{{x}^{3}}}{3}+C$

Вот это очень важно понимать: если производная функции всегда одна и та же, то первообразных у одной и той же функции бесконечно много. Просто к нашим первообразным мы можем дописывать любые числа-константы и получать новые.

Неслучайно, в пояснении к тем задачам, которые мы только что решали, было написано «Запишите общий вид первообразных». Т.е. уже заранее предполагается, что их не одна, а целое множество. Но, на самом деле, они отличаются лишь константой $C$ в конце. Потому в наших задачах мы исправим то, что мы не дописали.

Еще раз переписываем наши конструкции:

[Fleft( x right)=frac{3{{x}^{frac{5}{3}}}}{5}-3{{x}^{frac{4}{3}}}+4x+C]

В таких случаях следует дописывать, что $C$ — константа — $C=const$.

Во второй нашей функции мы получим следующую конструкцию:

[Fleft( x right)=-frac{1}{2{{x}^{2}}}+frac{6}{x}+12ln x+C]

И последняя:

[Fleft( x right)=frac{{{x}^{2}}}{2}+frac{4{{x}^{frac{3}{2}}}}{3}+x+C]

И вот теперь мы действительно получили то, что от нас требовалось в исходном условии задачи.

Решение задач на нахождение первообразных с заданной точкой

Сейчас, когда мы знаем о константах и об особенностях записи первообразных, вполне логично возникает следующий тип задач, когда из множества всех первообразных требуется найти одну-единственную такую, которая проходила бы через заданную точку. В чем состоит эта задача?

Дело в том, что все первообразные данной функции отличаются лишь тем, что они сдвинуты по вертикали на какое-то число. А это значит, что какую бы точку на координатной плоскости мы не взяли, обязательно пройдет одна первообразная, и, причем, только одна.

Итак, задачи, которые сейчас мы будем решать, сформулированы следующем образом: не просто найти первообразную, зная формулу исходной функции, а выбрать именно такую из них, которая проходит через заданную точку, координаты которой будут даны в условии задачи.

Пример № 1

[fleft( x right)=5{{x}^{4}}+6{{x}^{3}}-2x+6]

[M=left( -1;4 right)]

Для начала просто посчитаем каждое слагаемое:

[{{x}^{4}}to frac{{{x}^{5}}}{5}]

[{{x}^{3}}to frac{{{x}^{4}}}{4}]

[xto frac{{{x}^{2}}}{2}]

[6to 6x]

Теперь подставляем эти выражения в нашу конструкцию:

[Fleft( x right)=5cdot frac{{{x}^{5}}}{5}+6cdot frac{{{x}^{4}}}{4}-2cdot frac{{{x}^{2}}}{2}+6x+C]

[Fleft( x right)={{x}^{5}}+frac{3{{x}^{4}}}{2}-{{x}^{2}}+6x+C]

Эта функция должна проходить через точку $Mleft( -1;4 right)$. Что значит, что она проходит через точку? Это значит, что если вместо $x$ поставить везде $-1$, а вместо $Fleft( x right)$ — $-4$, то мы должны получить верное числовое равенство. Давайте так и сделаем:

[4={{left( -1 right)}^{5}}+frac{3cdot {{left( -1 right)}^{4}}}{2}-{{left( -1 right)}^{2}}+6cdot left( -1 right)+C]

Мы видим, что у нас получилось уравнение относительно $C$, поэтому давайте попробуем его решить:

[4=-1+frac{3}{2}-1-6+C]

[C=4+6+2-frac{3}{2}=10,5]

Давайте запишем то самое решение, которое мы искали:

[Fleft( x right)={{x}^{5}}+frac{3{{x}^{4}}}{2}-{{x}^{2}}+6x+10,5]

Пример № 2

[fleft( x right)={{left( x-3 right)}^{2}}]

[M=left( 2;-1 right)]

В первую очередь необходимо раскрыть квадрат разности по формуле сокращенного умножения:

[fleft( x right)={{x}^{2}}-6x+9]

Считаем:

[{{x}^{2}}to frac{{{x}^{3}}}{3}]

[xto frac{{{x}^{2}}}{2}]

[9to 9x]

Исходная конструкция запишется следующим образом:

[Fleft( x right)=frac{{{x}^{3}}}{3}-6cdot frac{{{x}^{2}}}{2}+9x+C]

[Fleft( x right)=frac{{{x}^{3}}}{3}-3{{x}^{2}}+9x+C]

Теперь давайте найдем $C$: подставим координаты точки $M$:

[-1=frac{8}{3}-12+18+C]

Выражаем $C$:

[C=-1-6-2frac{2}{3}=-9frac{2}{3}]

Осталось отобразить итоговое выражение:

[Fleft( x right)=frac{{{x}^{3}}}{3}-3{{x}^{2}}+9x-9frac{2}{3}]

Решение тригонометрических задач

В качестве финального аккорда к тому, что мы только что разобрали, предлагаю рассмотреть две более сложные задачи, в которых содержится тригонометрия. В них точно так же потребуется найти первообразные для всех функций, затем выбрать из этого множества одну-единственную, которая проходит через точку $M$ на координатной плоскости.

Забегая наперед, хотел бы отметить, что тот прием, который мы сейчас будем использовать для нахождения первообразных от тригонометрических функций, на самом деле, является универсальным приемом для самопроверки.

Задача № 1

[fleft( x right)=frac{1}{{{cos }^{2}}x}]

[M=left( frac{text{ }!!pi!!text{ }}{text{4}};-1 right)]

Вспомним следующую формулу:

[{{left( text{tg}x right)}^{prime }}=frac{1}{{{cos }^{2}}x}]

Исходя из этого, мы можем записать:

[Fleft( x right)=text{tg}x+C]

Давайте подставим координаты точки $M$ в наше выражение:

[-1=text{tg}frac{text{ }!!pi!!text{ }}{text{4}}+C]

[-1=1+C]

[C=-2]

Перепишем выражение с учетом этого факта:

[Fleft( x right)=text{tg}x-2]

Задача № 2

[fleft( x right)=frac{1}{{{sin }^{2}}x}]

[M=left( -frac{text{ }!!pi!!text{ }}{text{4}};2 right)]

Тут будет чуть сложнее. Сейчас увидите, почему.

Вспомним такую формулу:

[{{left( text{ctg}x right)}^{prime }}=-frac{1}{{{sin }^{2}}x}]

Чтобы избавится от «минуса», необходимо сделать следующее:

[{{left( -text{ctg}x right)}^{prime }}=frac{1}{{{sin }^{2}}x}]

Вот наша конструкция

[Fleft( x right)=-text{ctg}x+C]

Подставим координаты точки $M$:

[2=-text{ctg}left( -frac{text{ }!!pi!!text{ }}{4} right)+C]

[2=text{ctg}frac{text{ }!!pi!!text{ }}{text{4}}+C]

[2=1+C]

[C=1]

Итого запишем окончательную конструкцию:

[Fleft( x right)=-text{ctg}x+1]

Вот и все, о чем я хотел сегодня вам рассказать. Мы изучили сам термин первообразных, как считать их от элементарных функций, а также как находить первообразную, проходящую через конкретную точку на координатной плоскости.

Надеюсь, этот урок хоть немного поможет вам разобраться в этой сложной теме. В любом случае, именно на первообразных строятся неопределенные и неопределенные интегралы, поэтому считать их совершенно необходимо. На этом у меня все. До новых встреч!

Смотрите также:

1. Таблица первообразных
2. Интегрирование по частям
3. Решение задач B12: №448—455
4. Что такое ЕГЭ по математике 2011 и как его сдавать
5. Задача B4: случай с неизвестным количеством товара
6. Задача B15: что делать с квадратичной функцией

Заказать задачи по любым предметам можно здесь от 10 минут

Интеграл от синуса

Интеграл от синуса по таблице интегрирования равен: $$ int sin x dx = — cos x + C $$

Словами это читается так: интеграл от синуса равен сумме отрицательного косинуса и произвольной постоянной.

Пример 1

Найти интеграл от синус 2x: $$ int sin 2x dx $$

Решение

Напрямую интеграл взять не получится, так как аргумент синуса и знака дифференциала отличаются. Выполняем подведение под дифференциал $ 2x $ и добавляем перед интегралом дробь $ frac{1}{2} $: $$ int sin 2x dx = frac{1}{2} int sin 2x d(2x) = -frac{1}{2} cos 2x + C $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ int sin 2x dx = -frac{1}{2} cos 2x + C $$

Пример 2

Найти интеграл от синуса в квадрате: $$ int sin^2 x dx $$

Решение

В данном случае необходимо воспользоваться одной из тригонометрических формул. Конкретно формулой понижения степени синуса: $$ sin^2 x = frac{1-cos 2x}{2} $$ Заменяем выражение под интегралом: $$ int sin^2 x dx = int frac{1-cos 2x}{2} dx = frac{1}{2} int (1-cos 2x) dx = $$ $$ = frac{1}{2} int 1dx — frac{1}{2} int cos 2x dx = frac{1}{2}x — frac{1}{2}cdotfrac{1}{2}int cos 2x d(2x) = $$ $$ = frac{1}{2}x — frac{1}{4}sin 2x + C $$

Ответ

$$ int sin^2 x dx = frac{1}{2}x — frac{1}{4}sin 2x + C $$

Пример 3

Найти интеграл от синуса в кубе: $$ int sin^3 x dx $$

Решение

Здесь нужно вспомнить свойство степеней и учесть: $$ sin^3 x = sin x cdot sin^2 x $$ Подставляем, полученное выражение в интеграл и заносим $ sin x $ под знак дифференциала: $$ int sin^3 x dx = int sin x sin^2 x dx = — int sin^2 x d(cos x) = $$ Далее используем свойство $ sin^2 x = 1 — cos^2 x $: $$ = -int (1-cos^2 x) d(cos x) = -int d(cos x) + int cos^2 x d(cos x) = $$ $$ = — cos x + frac{cos^3 x}{3} + C = frac{1}{3} cos^3 x — cos x + C $$

Ответ

$$ int sin^3 x dx = frac{1}{3} cos^3 x — cos x + C $$

Пример 4

Вычислить определенный интеграл от синуса: $$ int_0^pi sin x dx $$

Решение

Вычисление начнем как в случае с неопределенным интегралом и в конце используем формулу Ньютона-Лейбница $ int_a^b f(x) dx = F(x) bigg |_a^b = F(b)-F(a) $: $$ int_0^pi sin x dx = -cos x bigg |_0^pi = -cos pi + cos 0 = -(-1) + 1 = 1+1=2 $$

Ответ

$$ int_0^pi sin x dx = 2 $$

ВИДЕО УРОК

Что такое первообразная и как она считается ?

ПРИМЕР:

Найдём производную:

f(x) = x³.

Находим её, пользуясь формулой:

Откуда

Это и есть определение
первообразной.

Аналогично запишем и
такое выражение:

Обобщим это правило и
выведем следующую формулу:

При   n = –1 
первообразная функция определяется следующим образом:
Учитывая,
что

а производная

Первообразной функции называется такая функция, производная которой равна
исходной функции.

Функция

y = F(x)

называется первообразной функции

y = f(x)

на промежутке  Х, если для любого  х ∈ Х  выполняется равенство:

F(x) = f(x).

Таблица первообразных
функций.

К каждому выражению в правой части таблицы необходимо прибавить константу.

Правила нахождения первообразных функций.

1. Первообразная функция суммы (разности) равна сумме (разности)
первообразных функций.

F(x + у) = F(x) + F(у),

F(x – у) = F(x) – F(у).

ПРИМЕР:

Найти первообразную для функции

у
= 4х³ + cos x.

РЕШЕНИЕ:

Первообразная суммы равна сумме
первообразных, тогда надо найти первообразную для каждой из представленных
функций.

f(x) = 4x³,  F(x)
= x⁴.

f(x) = cos x,  F(x) = sin x.

Тогда первообразная исходной
функции будет

у
= х⁴ + sin x

или любая функция вида

у
= х⁴ + sin x + C.

2. Если  F(x) –
первообразная для  f(x), то

k F(x)–
первообразная для функции  k f(x).

(Коэффициент можно выносить за функцию).

ПРИМЕР:

Найти первообразную для функции

у
= 8 sin x.

РЕШЕНИЕ:

Первообразной для  sin x  служит
минус  cos x.
Тогда первообразная исходной функции примет вид:

у
= –8 cos x.

ПРИМЕР:

Найти первообразную для функции

у
= 3x² + 4х + 5.

РЕШЕНИЕ:

Первообразной для  x²  служит

Первообразной для  x  служит

Первообразной для  1  служит  x.

Тогда первообразная исходной
функции примет вид:

у
= x³ + 2x² + 5 x.

3. Если  y = F(x) – первообразная для функции

y = f(x),

то первообразная для функции

y = f(kx + m)

служит функция

y = ¹/_k F(kx + m).

ПРИМЕР:

Найти первообразную для функции

у
= cos (7x).

РЕШЕНИЕ:

Первообразной для  cos x  служит  sin x. Тогда первообразная для функции

cos (7x)

будет функция

ПРИМЕР:

Найти первообразную для функции

у
= sin ^x/₂.

РЕШЕНИЕ:

Первообразной для  sin x  служит минус  cos x. Тогда первообразная для функции

у
= sin ^x/₂

будет функция

ПРИМЕР:

Найти первообразную для функции

у
= (–2х + 3)³.

РЕШЕНИЕ:

Первообразной для  x³  служит

Тогда первообразная для исходной
функции

у
= (–2х + 3)³.

будет функция

ПРИМЕР: