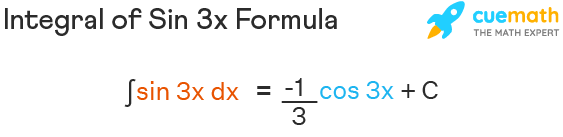Как найти первообразную sin3x

Предмет: Математика,


автор: anitusic

Ответы

Автор ответа: dedulja66let

1

Ответ:

Пошаговое объяснение:

Задана функция:

f(x) = sin (3x)

Найдем ее первообразную:

F(x) = — (1/3)·cos(3x) + C

C=0

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Другие предметы,
автор: Аноним

Как записать восемнадцатая с точкой

1 месяц назад

Предмет: Беларуская мова,
автор: Алёнка123456789012

Прыклад пэуна-асабовых сказау

1 месяц назад

Предмет: Русский язык,
автор: anastasia561u

Составьте предложения с данными словами. Какие это части речи?
Что бы, чтобы, также, так же, зато, за то.

1 месяц назад

Предмет: Математика,
автор: sizovan05021985

Помогите пожалуйста вычисли рационально 64+16+8+12

6 лет назад

Предмет: Математика,
автор: menzik79

1) длину прямоугольника увеличили на 10% и ширину — на 20%. на сколько процентов увеличилась площадь прямоугольника? А. на 40%; В. на 32%; С. на 25%; D. на 30%

6 лет назад

Integral of sin 3x is given by (-1/3) cos 3x + C. The integral of sin 3x is called the anti-derivative of sin 3x as integration is the reverse process differentiation. Sin 3x is an important trigonometric formula that is used to solve various problems in trigonometry. The integral of sin 3x can be calculated using the substitution method and using the sin 3x formula.

In this article, we will calculate the integral of sin 3x, prove it using the substitution method and sin 3x formula and determine the definite integral of sin 3x using different limits.

1.	What is Integral of Sin 3x?
2.	Integral of Sin 3x Formula
3.	Integral of Sin 3x Using Substitution Method
4.	Integral of Sin 3x Using Sin 3x Formula
5.	Definite Integral of Sin 3x
6.	FAQs on Integral of Sin 3x

What is Integral of Sin 3x?

The integral of sin 3x can be calculated using the formula for the integral of sin ax which is given by ∫sin (ax) dx = (-1/a) cos ax + C. Mathematically, the integral of sin 3x is written as ∫sin 3x dx = (-1/3) cos 3x + C, where C is the constant of integration, dx denotes that the integration of sin 3x is with respect to x, ∫ is the symbol for integration. The integral of sin 3x can also be evaluated using the substitution method and sin 3x formula.

Integral of Sin 3x Formula

Sin 3x formula is given by sin 3x = 3 sin x — 4 sin³x and the formula for the integral of sin 3x is given by, ∫sin 3x dx = (-1/3) cos 3x + C, where C is the constant of integration.

Integral of Sin 3x Using Substitution Method

Now, we know that the integral of sin 3x is (-1/3) cos 3x + C, where C is the constant of integration. Let us prove this using the substitution method. We will use the following formulas of integration and differentiation:

• ∫sin x dx = -cos x + C
• d(ax)/dx = a

Assume 3x = u, then differentiating 3x = u with respect to x, we have 3dx = du ⇒ dx = (1/3)du. Using the above formulas, we have

∫sin 3x dx = ∫sin u (du/3)

⇒ ∫sin 3x dx = (1/3) ∫sin u du

⇒ ∫sin 3x dx = (1/3) (-cos u + C) [Because ∫sin x dx = -cos x + C]

⇒ ∫sin 3x dx = (-1/3) cos u + C/3

⇒ ∫sin 3x dx = (-1/3) cos 3x + K, where K = C/3

Hence, we have derived the integral of sin 3x using the substitution method.

Integral of Sin 3x Using Sin 3x Formula

We know that the sin 3x formula is sin 3x = 3 sin x — 4 sin³x. Next, we will prove that the integration of sin 3x is given by (-1/3) cos 3x + C using the sin 3x formula. Before proving the integral of sin 3x, we will derive the integral of sin cube x, that is, sin³x. We will use the following formulas to prove the integral of sin³x:

• cos²x + sin²x = 1 ⇒ sin²x = 1 — cos²x
• ∫sin x dx = -cos x dx

∫sin³x dx = ∫sin x. sin²x dx

= ∫sin x.(1 — cos²x) dx

= ∫sin x dx — ∫sin x. cos²x dx — (1)

= I₁ — I₂ , where I₁ = ∫sin x dx and I₂ = ∫sin x. cos²x dx

Now, I₁ = ∫sin x dx = -cos x + C₁, where C₁ is the constant of integration —- (2)

For I₂ = ∫sin x. cos²x dx, assume cos x = u ⇒ -sin x dx = du ⇒ sin x dx = -du

I₂ = ∫sin x. cos²x dx

= ∫u² (-du)

= — ∫u² du

= — u³/3 + C₂, where C₂ is the constant of integration

= (-1/3) cos³x + C₂ —- (3)

Subsitute the values from (2) and (3) in (1),

∫sin³x dx = (-cos x + C₁) — ((-1/3) cos³x + C₂)

= -cos x + (1/3) cos³x + C₁ — C₂

= -cos x + (1/3) cos³x + C, where C = C₁ — C₂

⇒ ∫sin³x dx = -cos x + (1/3) cos³x + C — (4)

Now that we have derived the integral of sin³x, we will use this formula along with some other formulas to derive the integral of sin 3x:

• ∫sin x dx = -cos x dx
• ∫sin³x dx = -cos x + (1/3) cos³x + C
• sin 3x = 3 sin x — 4 sin³x
• cos 3x = 4cos³x — 3 cos x

Using the above formulas, we have

∫sin 3x dx = ∫(3 sin x — 4 sin³x) dx

= 3 ∫sin x dx — 4 ∫sin³x dx

= 3(-cos x) — 4(-cos x + (1/3) cos³x) + C, where C is the constant of integration

= -3 cos x + 4 cos x — (4/3)cos³x + C

= cos x — (4/3)cos³x + C

= (1/3)(3cos x — 4cos³x + 3C)

= (1/3)(-cos 3x + 3C) [Because cos 3x = 4cos³x — 3 cos x]

= (-1/3) cos 3x + C

Hence, we have derived the integration of sin 3x using the sin 3x formula.

Definite Integral of Sin 3x

We have proved that the integral of sin 3x is (-1/3) cos 3x + C. Now, we will determine the values of the definite integral of sin 3x with different limits. First, we will take the limits from 0 to π/3.

Definite Integral of Sin 3x From 0 to π/3

(begin{align}int_{0}^{frac{pi}{3}}sin 3x dx &= left [ -frac{1}{3}cos 3x+C right ]_0^frac{pi}{3}\&=left ( -frac{1}{3}cos 3frac{pi}{3}+C right )-left ( -frac{1}{3}cos 3(0)+Cright )\&=-frac{1}{3}cos pi+C + frac{1}{3}cos 0-C\&= -frac{1}{3}(-1)+frac{1}{3}(1)\&=frac{2}{3}end{align})

Hence the value of the definite integral of sin 3x with limits from 0 to π/3 is equal to 2/3.

Definite Integral of Sin 3x From 0 to Pi

(begin{align}int_{0}^{pi}sin 3x dx &= left [ -frac{1}{3}cos 3x+C right ]_0^pi\&=left ( -frac{1}{3}cos 3pi+C right )-left ( -frac{1}{3}cos 3(0)+Cright )\&=-frac{1}{3}cos 3pi+C + frac{1}{3}cos 0-C\&= -frac{1}{3}(-1)+frac{1}{3}(1)\&=frac{2}{3}end{align})

Hence the value of the definite integral of sin 3x with limits from 0 to π is equal to 2/3.

Definite Integral of Sin 3x From 0 to Pi/2

(begin{align}int_{0}^{frac{pi}{2}}sin 3x dx &= left [ -frac{1}{3}cos 3x+C right ]_0^frac{pi}{2}\&=left ( -frac{1}{3}cos 3frac{pi}{2}+C right )-left ( -frac{1}{3}cos 3(0)+Cright )\&=-frac{1}{3}cos frac{3pi}{2}+C + frac{1}{3}cos 0-C\&= -frac{1}{3}(0)+frac{1}{3}(1)\&=frac{1}{3}end{align})

Hence the value of the definite integration of sin 3x with limits from 0 to π/2 is equal to 1/3.

Important Notes on Integral of Sin 3x

• The easiest way to determine the integral of sin 3x is using the formula ∫sin (ax) dx = (-1/a) cos ax + C.
• The integral of sin 3x is (-1/3) cos 3x + C and the integral of sin cube x is ∫sin³x dx -cos x + (1/3) cos³x + C.

Related Topics

• Integral of Tan 2x
• Cos 3x
• Sin 3x

FAQs on Integral of Sin 3x

What is Integral of Sin 3x in Trigonometry?

In trigonometry, the integral of sin 3x is written as ∫sin 3x dx = (-1/3) cos 3x + C, where C is the constant of integration.

How to Find the Integral of Sin 3x?

The integral of sin 3x can be calculated using the formula for the integral of sin ax which is given by ∫sin (ax) dx = (-1/a) cos ax + C. It can also be calculated using the substitution method and sin 3x formula.

What is the Definite Integral of Sin 3x from 0 to pi?

The value of the definite integral of sin 3x with limits from 0 to π is equal to 2/3.

What is the Integration of Sin³x?

The integral of sin cube x is given by ∫sin³x dx = -cos x + (1/3) cos³x + C.

What is the Integral of Sin 2x?

The integral of sin 2x dx is written as ∫ sin 2x dx = -(cos 2x)/2 + C, where C is the integration constant.

Найдите правильный ответ на вопрос ✅ «Найти первообразную: f (x) = sin3x …» по предмету 📘 Алгебра, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.

Смотреть другие ответы

Tip: See my list of the Most Common Mistakes in English. It will teach you how to avoid mis­takes with com­mas, pre­pos­i­tions, ir­reg­u­lar verbs, and much more.

Integrating the third power of $sin(x)$ (or any odd power, for that matter), is an easy task (unlike $∫ sin^2(x),dx$, which requires a little trick). All you have to do is write the expression as $sin(x)⋅(text{even power of }sin)$, rewrite the even power using the formula $sin^2(x) = 1-cos^2(x)$,
and apply the substitution $u = cos(x)$ (i.e. $du = -sin(x)dx$). Let’s see it in practice:

$$
∫ sin^3(x),dx = ∫ sin(x)sin^2(x),dx = ∫ sin(x)(1-cos^2(x)),dx = l.∫ -(1-u^2),dur|_{u = cos(x)} = -u + frac{u^3}3 + c = frac13 cos^3(x)-cos(x) + c,.
$$

The same approach works for any odd power of $sin(x)$ (or $cos(x)$), only the resulting expressions get slightly more complicated. For example,

$$
∫ sin^5(x),dx = ∫ sin(x)(sin^2(x))^2,dx = ∫ sin(x)(1-cos^2(x))^2,dx \
= ∫ -(1-u^2)^2,du = ∫ (-u^4+2u^2-1),du = -frac{u^5}5 + frac{2u^3}3 — u + c \
= -frac15 cos^5(x) + frac23 cos^3(x)-cos(x) + c,.
$$

By the way, I have written several educational ebooks. If you get a copy, you can learn new things and support this website at the same time—why don’t you check them out?

Use the image

You can use the image on another website, provided that you link to the source article. If you share it on Twitter or Facebook, I kindly ask you to tag my profile @JakubMarian.

If you share it on reddit, please, share a link to the whole article and give credit to my subreddit r/JakubMarian in the comments.

Вася Иванов

Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.