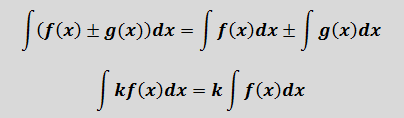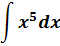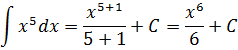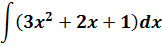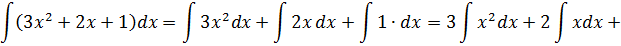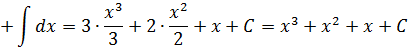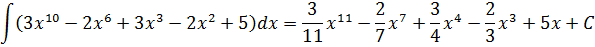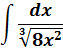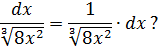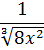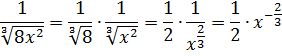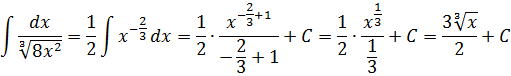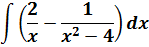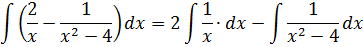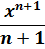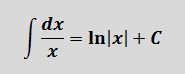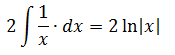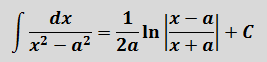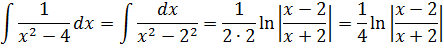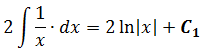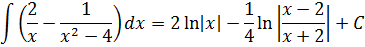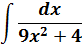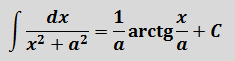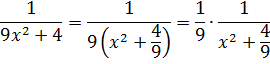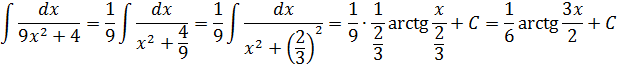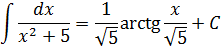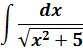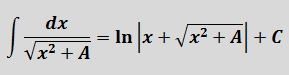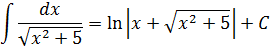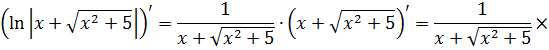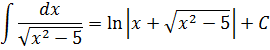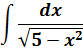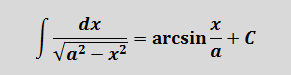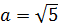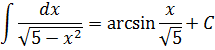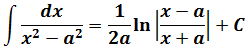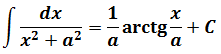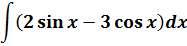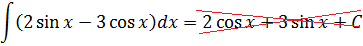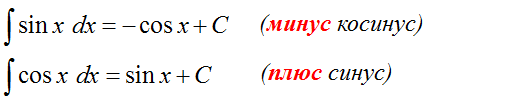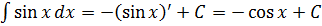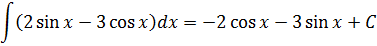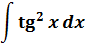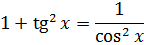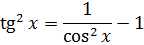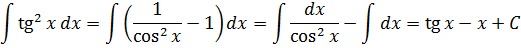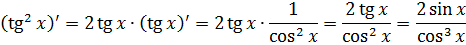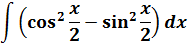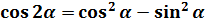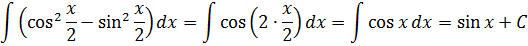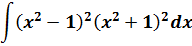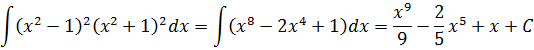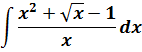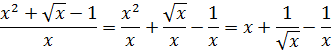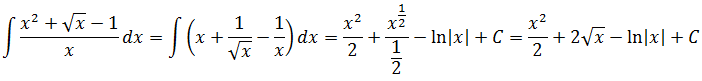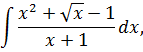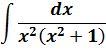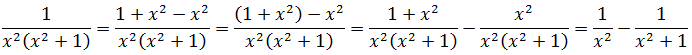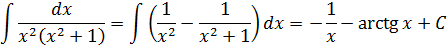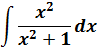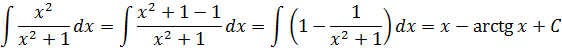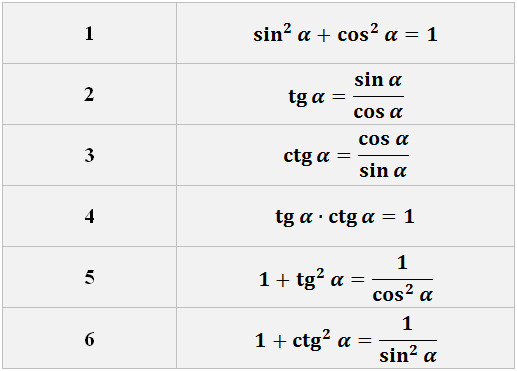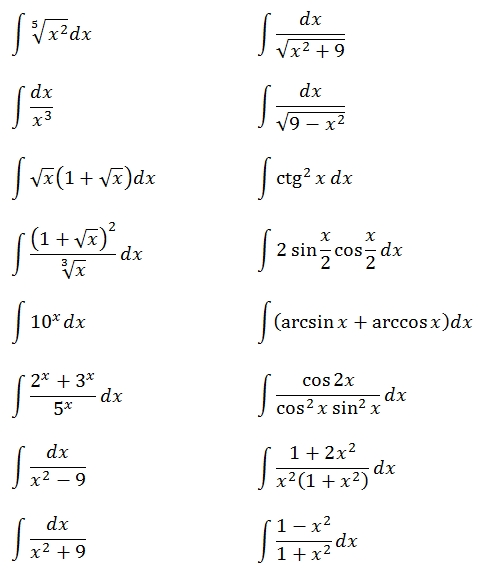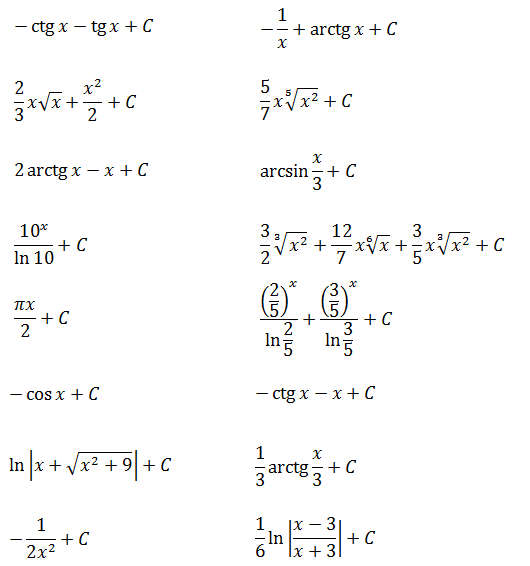Как найти первообразную степенной функции

Содержание:

• Формула
• Примеры вычисления интеграла степенной функции

Формула

Интеграл от степенной функции равен этой же функции в степени на единицу больше, деленной
на эту же степень, плюс постоянная интегрирования.

Заметим, что если $x$ в некоторой
степени находится в знаменателе, то применяют свойство $frac{1}{x^{n}}=x^{-n}$ и далее интегрируют по указанной формуле.

Примеры вычисления интеграла степенной функции

Читать дальше: интеграл корня.

        И снова здравствуйте, друзья!

        Как я и обещал, с этого урока мы начнём бороздить бескрайние просторы поэтического мира интегралов и приступим к решению самых разнообразных (порой, очень красивых) примеров.

        Чтобы грамотно ориентироваться во всём интегральном многообразии и не заблудиться, нам потребуется всего четыре вещи:

        1) Таблица интегралов. Все подробности о ней — в предыдущем материале. Как именно с ней работать — в этом.

        2) Свойства линейности неопределённого интеграла (интеграл суммы/разности и произведения на константу).

        3) Таблица производных и правила дифференцирования.

        Да-да, не удивляйтесь! Без умения считать производные, в интегрировании ловить совершенно нечего. Согласитесь, бессмысленно, например, учиться делению, не умея умножать. И очень скоро вы увидите, что без отточенных навыков дифференцирования не посчитать ни один сколь-нибудь серьёзный интеграл, выходящий за рамки элементарных табличных.

        4) Методы интегрирования.

        Их очень и очень много. Для конкретного класса функций — свой. Но среди всего их богатого разнообразия выделяется три базовых:

         – метод подведения функции под знак дифференциала,

         – метод замены переменной,

         – метод интегрирования по частям.

        О каждом из них — в отдельных уроках.

        А теперь, наконец, приступим к решению долгожданных примеров. Чтобы не скакать из раздела в раздел, я продублирую ещё разок весь джентльменский набор, который пригодится для нашей дальнейшей работы. Пусть весь инструментарий будет под рукой.)

        Прежде всего, это таблица интегралов:

        Кроме того, нам понадобятся базовые свойства неопределённого интеграла (свойства линейности):

       Что ж, необходимая снаряга подготовлена. Пора в путь!

Прямое применение таблицы

        В данном параграфе будут рассматриваться самые простые и безобидные примеры. Алгоритм здесь прост до ужаса:

        1) Смотрим в таблицу и ищем нужную формулу (формулы);

        2) Применяем свойства линейности (где требуется);

        3) Осуществляем превращение по табличным формулам и прибавляем в конце константу С (не забываем!);

        4) Записываем ответ.

Итак, поехали.)

Пример 1

        Такой функции в нашей таблице нет. Зато есть интеграл от степенной функции в общем виде (вторая группа). В нашем случае n = 5. Вот и подставляем пятёрку вместо n и аккуратно считаем результат:

        Готово.

        Разумеется, этот пример совсем примитивный. Чисто для знакомства.) Зато умение интегрировать степени позволяет легко считать интегралы от любых многочленов и прочих степенных конструкций.

        Пример 2

        Под интегралом сумма. Ну и ладно. У нас на этот случай есть свойства линейности. Разбиваем наш интеграл на три отдельных, выносим все константы за знаки интегралов и считаем каждый по таблице (группа 1-2):

           

           

        Прошу обратить внимание: константа С появляется именно в тот момент, когда исчезают ВСЕ знаки интеграла! Конечно, после этого приходится её постоянно таскать за собой. А что делать…

        Разумеется, так подробно расписывать обычно не требуется. Это чисто для понимания сделано. Чтобы суть уловить.)  

        Например, очень скоро, особо не раздумывая, вы в уме будете давать ответ к монстрам типа:

        Многочлены — самые халявные функции в интегралах.) А уж в диффурах, в физике, в сопромате и прочих серьёзных дисциплинах интегрировать многочлены придётся постоянно. Привыкайте.)

        Следующий примерчик будет чуть покруче.

        Пример 3

        Надеюсь, всем понятно, что наше подынтегральное выражение можно расписать вот так:

           

        Подынтегральная функция отдельно, а множитель dx (значок дифференциала) — отдельно.

        Замечание: в этом уроке множитель dx в процессе интегрирования пока никак не участвует, и мы на него пока что мысленно «забиваем». Работаем только с подынтегральной функцией. Но забывать про него не будем. Совсем скоро, буквально на следующем уроке, посвящённом подведению функции под знак дифференциала, мы про него вспомним. И ощутим всю важность и мощь этого значка в полную силу!)

        А пока наш взор обращён на подынтегральную функцию 

           

        Не очень похоже на степенную функцию, но это она. Если вспомнить школьные свойства корней и степеней, то вполне можно преобразовать нашу функцию:

           

        А икс в степени минус две трети — это уже табличная функция! Вторая группа, n=-2/3. А константа 1/2 нам не помеха. Выносим её наружу, за знак интеграла, и прямо по формуле считаем:

           

        В этом примере нам помогли элементарные свойства степеней. И так надо делать в большинстве случаев, когда под интегралом стоят одинокие корни или дроби. Посему пара практических советов при интегрировании степенных конструкций:

        Заменяем дроби степенями с отрицательными показателями;

        Заменяем корни степенями с дробными показателями.

        А вот в окончательном ответе переход от степеней обратно к дробям и корням — дело вкуса. Лично я перехожу обратно — так эстетичнее, что ли.

        И, пожалуйста, аккуратно считаем все дроби! Внимательно следим за знаками и за тем, что куда идёт — что в числитель, а что знаменатель.

        Что? Надоели уже скучные степенные функции? Ну ладно! Берём быка за рога!

        Пример 4

        Если сейчас привести всё под интегралом к общему знаменателю, то можно застрять на этом примере всерьёз и надолго.) Но, присмотревшись повнимательнее к подынтегральной функции, можно заметить, что наша разность состоит из двух табличных функций. Так что не будем извращаться, а вместо этого разложим наш интеграл на два:

           

        Первый интеграл — обычная степенная функция, (2-я группа, n = -1): 1/x = x^-1.

        Традиционная наша формула для первообразной степенной функции

           

        здесь не работает, но зато у нас для n = -1 есть достойная альтернатива — формула с натуральным логарифмом. Вот эта:

           

        Тогда, согласно этой формуле, первая дробь проинтегрируется так:

        

        А вторая дробь — тоже табличная функция! Узнали? Да! Это седьмая формула с «высоким» логарифмом:

       

        Константа «а» в этой формуле равна двойке: a=2.

           

        Важное замечание: Обратите внимание, константу С при промежуточном интегрировании я нигде не приписываю! Почему? Потому что она пойдёт в окончательный ответ всего примера. Этого вполне достаточно.) Строго говоря, константу надо писать после каждого отдельного интегрирования — хоть промежуточного, хоть окончательного: так уж неопределённый интеграл требует…) 

        Например, после первого интегрирования я должен был бы написать:

        

        После второго интегрирования:

        

        Но вся фишка в том, что сумма/разность произвольных констант — это тоже некоторая константа! В нашем случае для окончательного ответа нам надо из первого интеграла вычесть второй. Тогда у нас получится разность двух промежуточных констант:

        С₁-С₂ 

        И мы имеем полное право эту самую разность констант заменить одной константой! И просто переобозначить её привычной нам буквой «С». Вот так:

        С₁-С₂ = С

        Вот и приписываем эту самую константу С к окончательному результату и получаем ответ:

        Да-да, дроби они такие! Многоэтажные логарифмы при их интегрировании — самое обычное дело. Тоже привыкаем.)

        Запоминаем:

        При промежуточном интегрировании нескольких слагаемых константу С после каждого из них можно не писать. Достаточно включить её в окончательный ответ всего примера. В самом конце.

        Следующий пример тоже с дробью. Для разминки.)

        Пример 5

        В таблице, понятное дело, такой функции нет. Но зато есть похожая функция: 

           

        Это самая последняя, восьмая формула. С арктангенсом.

        Вот эта:

        И нам сам бог велел подстроить наш интеграл под эту формулу! Но есть одна проблемка: в табличной формуле перед х² никакого коэффициента нету, а у нас — девятка. Не можем пока что напрямую воспользоваться формулой. Но в нашем случае проблема вполне решаема. Вынесем эту девятку сначала за скобки, а потом вообще уведём за пределы нашей дроби.)

           

        А новая дробь — уже нужная нам табличная функция под номером 8! Здесь а²=4/9. Или а=2/3.

        Всё. Выносим 1/9 за знак интеграла и пользуемся восьмой формулой:

           

        Вот такой ответ. Этот пример, с коэффициентом перед х², я специально так подобрал. Чтобы ясно было, что делать в таких случаях. Если перед х² никакого коэффициента нет, то такие дроби тоже будут в уме интегрироваться.

        Например:

        Здесь а² = 5, поэтому само «а» будет «корень из пяти». В общем, вы поняли.)

        А теперь немного видоизменим нашу функцию: напишем знаменатель под корнем.) Вот такой интеграл теперь будем брать:

        Пример 6

        В знаменателе появился корень. Естественно, изменилась и соответствующая формула для интегрирования, да.) Опять лезем в таблицу и ищем подходящую. Корни у нас есть в формулах 5-й и 6-й групп. Но в шестой группе под корнями только разность. А у нас — сумма. Значит, работаем по пятой формуле, с «длинным» логарифмом:

        Число А у нас — пятёрка. Подставляем в формулу и получаем:

        И все дела. Это ответ. Да-да, так просто!)

        Если закрадываются сомнения, то всегда можно (и нужно) проверить результат обратным дифференцированием. Проверим? А то вдруг, лажа какая-нибудь?

        Дифференцируем (на модуль внимания не обращаем и воспринимаем его как обычные скобки):

        Всё честно.

        Кстати, если в подынтегральной функции под корнем поменять знак с плюса на минус, то формула для интегрирования останется той же самой. Не случайно в таблице под корнем стоит плюс/минус.

        Например:

        Важно! В случае минуса, на первом месте под корнем должно стоять именно х², а на втором — число. Если же под корнем всё наоборот, то и соответствующая табличная формула будет уже другая!

        Пример 7

        Под корнем снова минус, но х² с пятёркой поменялись местами. Похоже, но не одно и то же… На этот случай в нашей таблице тоже есть формулка.) Формула номер шесть, с ней мы ещё не работали:

        А вот теперь — аккуратно. В предыдущем примере у нас пятёрка выступала в роли числа A. Здесь же пятёрка будет выступать уже в роли числа а²!

        Поэтому для правильного применения формулы не забываем извлечь корень из пятёрки:  

           

        И теперь пример решается в одно действие.

        Вот так вот! Всего лишь поменялись местами слагаемые под корнем, а результат интегрирования изменился существенно! Логарифм и арксинус… Так что, пожалуйста, не путайте эти две формулы! Хотя подынтегральные функции и очень похожи…

        Бонус:

        В табличных формулах 7-8 перед логарифмом и арктангенсом присутствуют коэффициенты 1/(2а) и 1/а соответственно. И в тревожной боевой обстановке при записи этих формул даже закалённые учёбой ботаны частенько путаются, где просто 1/а, а где 1/(2а). Вот вам простой приёмчик для запоминания.

        В формуле №7       

           

        в знаменателе подынтегральной функции стоит разность квадратов х² — а². Которая, согласно боянной школьной формуле, раскладывается как (х-а)(х+а). На два множителя. Ключевое слово — два. И эти две скобки при интегрировании идут в логарифм: с минусом вверх, с плюсом — вниз.) И коэффициент перед логарифмом тоже 1/(2а).

        А вот в формуле №8   

           

        в знаменателе дроби стоит сумма квадратов. Но сумма квадратов x²+a² неразложима на более простые множители. Поэтому, как ни крути, в знаменателе так и останется один множитель. И коэффициент перед арктангенсом тоже будет 1/а.

        А теперь для разнообразия проинтегрируем что-нибудь из тригонометрии.)

        Пример 8

         Пример простой. Настолько простой, что народ, даже не глядя в таблицу, тут же радостно ответ пишет и… приехали.

        Следим за знаками! Это самая распространённая ошибка при интегрировании синусов/косинусов. Не путаем с производными!

        Да, (sin x)’ = cos x и (cos x)’ = —sin x.

        Но!

        

        Поскольку производные народ обычно худо-бедно помнит, то, чтобы не путаться в знаках, приём для запоминания интегралов тут очень простой:

        Интеграл от синуса/косинуса = минус производная от тех же синуса/косинуса.

        Например, мы ещё со школы знаем, что производная синуса равна косинусу:

        (sin x)’ = cos x.

        Тогда для интеграла от того же синуса будет справедливо:

           

        И всё.) С косинусом то же самое.

        Исправляем теперь наш пример:

Предварительные элементарные преобразования подынтегральной функции

        До этого момента были самые простенькие примеры. Чтобы прочувствовать, как работает таблица и не ошибаться в выборе формулы.)

        Конечно, мы делали кое-какие простенькие преобразования — множители выносили, на слагаемые разбивали. Но ответ всё равно так или иначе лежал на поверхности.) Однако… Если бы вычисление интегралов ограничивалось только прямым применением таблицы, то вокруг была бы сплошная халява и жить стало бы скучно.)

        А теперь разберём примеры посолиднее. Такие, где впрямую, вроде бы, ничего и не решается. Но стоит вспомнить буквально пару-тройку элементарных школьных формул или преобразований, как дорога к ответу становится простой и понятной.

        Применение формул тригонометрии

        Продолжим развлекаться с тригонометрией.

        Пример 9

        Такой функции в таблице и близко нет. Зато в школьной тригонометрии есть такое малоизвестное тождество:

           

        Выражаем теперь из него нужный нам квадрат тангенса и вставляем под интеграл:

           

        Зачем это сделано? А затем, что после такого преобразования наш интеграл сведётся к двум табличным и будет браться в уме!

        Смотрите:

        А теперь проанализируем наши действия. На первый взгляд, вроде бы, всё проще простого. Но давайте задумаемся вот над чем. Если бы перед нами стояла задача продифференцировать ту же самую функцию, то мы бы точно знали, что именно надо делать — применять формулу производной сложной функции:

        И всё. Простая и безотказная технология. Работает всегда и гарантированно приводит к успеху.

        А что же с интегралом? А вот тут нам пришлось порыться в тригонометрии, откопать какую-то малопонятную формулу в надежде, что она нам как-то поможет выкрутиться и свести интеграл к табличному. И не факт, что помогла бы она нам, совсем не факт… Именно поэтому интегрирование — более творческий процесс, нежели дифференцирование. Искусство, я бы даже сказал. И это ещё не самый сложный пример. То ли ещё будет!

        Пример 10

        Что, внушает? Таблица интегралов пока бессильна, да. Но, если снова заглянуть в нашу сокровищницу тригонометрических формул, то можно откопать весьма и весьма полезную формулу косинуса двойного угла:

        Вот и применяем эту формулу к нашей подынтегральной функции. В роли «альфа» у нас х/2.

        Получаем:

        Эффект потрясающий, правда?

        Эти два примера наглядно показывают, что предварительное преобразование функции перед интегрированием вполне допускается и порой колоссально облегчает жизнь! И в интегрировании эта процедура (преобразование подынтегральной функции) на порядок более оправдана, чем при дифференцировании. В дальнейшем всё увидите.)

        Разберём ещё парочку типовых преобразований.

        Формулы сокращённого умножения, раскрытие скобок, приведение подобных и метод почленного деления.

        Обычные банальные школьные преобразования. Но порой только они и спасают, да.)

        Пример 11

        Если бы мы считали производную, то никаких проблем: формула производной произведения и — вперёд. Но стандартной формулы для интеграла от произведения не существует. И единственный выход здесь — раскрыть все скобки, чтобы под интегралом получился многочлен. А уж многочлен мы как-нибудь проинтегрируем.) Но скобки раскрывать тоже будем с умом: формулы сокращённого умножения — штука мощная!

        (x² — 1)²(x² + 1)² = ((x² — 1)(x² + 1))² = ((x²)² — 1²)² = (x⁴ — 1)² = x⁸ — 2x⁴ + 1

           А теперь считаем:

И все дела.)

        Пример 12

        Опять же, стандартной формулы для интеграла от дроби не существует. Однако в знаменателе подынтегральной дроби стоит одинокий икс. Это в корне меняет ситуацию.) Поделим почленно числитель на знаменатель, сведя нашу жуткую дробь к безобидной сумме табличных степенных функций:

        Особо комментировать процедуру интегрирования степеней не буду: не маленькие уже.)

        Интегрируем сумму степенных функций. По табличке.)

        Вот и все дела.) Кстати, если бы в знаменателе сидел не икс, а, скажем, х+1, вот так:

        то этот фокус с почленным делением уже так просто не прошёл бы. Именно из-за наличия корня в числителе и единицы в знаменателе. Пришлось бы замену вводить и избавляться от корня. Но такие интегралы гораздо сложнее. О них — в других уроках.

        Видите! Стоит только чуть-чуть видоизменить функцию — тут же меняется и подход к её интегрированию. Порой кардинально!) Нету чёткой стандартной схемы. К каждой функции — свой подход. Иногда даже уникальный.)

        В некоторых случаях преобразования в дробях ещё более хитрые.

        Пример 13

        А здесь как можно свести интеграл к набору табличных? Здесь можно ловко извернуться добавлением и вычитанием выражения x² в числителе дроби с последующим почленным делением. Очень искусный приём в интегралах! Смотрите мастер-класс!

        И теперь, если заменить исходную дробь на разность двух дробей, то наш интеграл распадается на два табличных — уже знакомую нам степенную функцию и арктангенс (формула 8):

        Ну, что тут можно сказать? Вау!

        Этот трюк с добавлением/вычитанием слагаемых в числителе — очень популярен в интегрировании рациональных дробей. Очень! Рекомендую взять на заметку.

        Пример 14

        Здесь тоже рулит эта же технология. Только добавлять/вычитать надо единичку, чтобы из числителя выделить выражение, стоящее в знаменателе:

        Вообще говоря, рациональные дроби (с многочленами в числителе и знаменателе) — отдельная очень обширная тема. Дело всё в том, что рациональные дроби — один из очень немногих классов функций, для которых универсальный способ интегрирования существует. Метод разложения на простейшие дроби вкупе с методом неопределённых коэффициентов. Но способ этот очень трудоёмкий и обычно применяется как тяжёлая артиллерия. Ему будет посвящён не один урок. А пока что тренируемся и набиваем руку на простых функциях.

        Подытожим сегодняшний урок.

        Сегодня мы подробно рассмотрели, как именно пользоваться таблицей, со всеми нюансами, разобрали множество примеров (и не самых тривиальных) и познакомились с простейшими приёмами сведения интегралов к табличным. И так мы теперь будем поступать всегда. Какая бы страшная функция ни стояла под интегралом, с помощью самых разнообразных преобразований мы будем добиваться того, чтобы, рано или поздно, наш интеграл, так или иначе, свёлся к набору табличных.

        Несколько практических советов.

        1) Если под интегралом дробь, в числителе которой сумма степеней (корней), а в знаменателе — одинокая степень икса, то используем почленное деление числителя на знаменатель. Заменяем корни степенями с дробными показателями и работаем по формулам 1-2.         

        2) В тригонометрических конструкциях в первую очередь пробуем базовые формулы тригонометрии — двойного/тройного угла, основные тригонометрические тождества: 

        

        Может очень крупно повезти. А может и нет…

        3) Где нужно (особенно в многочленах и дробях), применяем формулы сокращённого умножения:

(a+b)² = a²+2ab+b²

(a-b)² = a²-2ab+b²

(a-b)(a+b) = a²-b² 

        и так далее…

        4) При интегрировании дробей с многочленами пробуем искусственно выделить в числителе выражение(я), стоящее(щие) в знаменателе. Очень часто дробь упрощается и интеграл сводится к комбинации табличных.

        Ну что, друзья? Я вижу, интегралы вам начинают нравиться. Тогда набиваем руку и решаем примеры самостоятельно.) Сегодняшнего материала вполне достаточно, чтобы успешно с ними справиться.

           

        Что? Не знаете, как интегрировать арксинус/арккосинус? Да! Мы этого ещё не проходили.) Но здесь их напрямую интегрировать и не нужно. И да поможет вам школьный курс!)

        Ответы (в беспорядке):

        

        Для лучших результатов настоятельно рекомендую приобрести сборник задач по матану Г.Н. Бермана. Классная штука!

        А у меня на сегодня всё. Успехов!

Таблица и правила нахождения первообразных

2 августа 2015

• Таблица первообразных

На этой странице вы найдёте:

1. Собственно, таблицу первообразных — её можно скачать в формате PDF и распечатать;

2. Видео, посвящённое тому, как этой таблицей пользоваться;

3. Кучу примеров вычисления первообразной из различных учебников и контрольных работ.

В самом видео мы разберём множество задач, где требуется посчитать первообразные функций, зачастую довольно сложных, но главное — не являющихся степенными. Все функции, сведённые в таблицу, предложенную выше, необходимо знать наизусть, подобно производным. Без них невозможно дальнейшее изучение интегралов и их применение для решения практических задач.

Сегодня мы продолжаем заниматься первообразными и переходим у чуть более сложной теме. Если в прошлый раз мы рассматривали первообразные только от степенных функций и чуть более сложных конструкций, то сегодня мы разберем тригонометрию и многое другое.

Как я говорил на прошлом занятии, первообразные в отличие от производных, никогда не решаются «напролом» с помощью каких-либо стандартных правил. Более того, плохая новость состоит в том, что в отличие от производной, первообразная вообще может не считаться. Если мы напишем совершенно случайную функцию и попытаемся найти ее производную, то это с очень большой вероятностью у нас получится, а вот первообразная практически никогда в этом случае не посчитается. Но есть и хорошая новость: существует довольно обширный класс функций, называемых элементарными, первообразные от которых очень легко считаются. А все прочие более сложные конструкции, которые дают на всевозможных контрольных, самостоятельных и экзаменах, на самом деле, составляются из этих элементарных функций путем сложения, вычитания и других несложных действий. Первообразные таких функций давно посчитаны и сведены в специальные таблицы. Именно с такими функциями и таблицами мы будем сегодня работать.

Но начнем мы, как всегда, с повторения: вспомним, что такое первообразная, почему их бесконечно много и как определить их общий вид. Для этого я подобрал две простенькие задачки.

Решение легких примеров

Пример № 1

[fleft( x right)=frac{1}{1+{{x}^{2}}}]

[M=left( sqrt{3};frac{text{ }!!pi!!text{ }}{6} right)]

Сразу заметим, что $frac{text{ }!!pi!!text{ }}{6}$ и вообще наличие $text{ }!!pi!!text{ }$ сразу намекает нам, что искомая первообразная функции связана с тригонометрией. И, действительно, если мы посмотрим в таблицу, то обнаружим, что $frac{1}{1+{{x}^{2}}}$ — не что иное как $text{arctg}x$. Так и запишем:

[Fleft( x right)=text{arctg}x+C]

Для того чтобы найти, необходимо записать следующее:

[frac{pi }{6}=text{arctg}sqrt{3}+C]

[frac{text{ }!!pi!!text{ }}{6}=frac{text{ }!!pi!!text{ }}{3}+C]

[C=frac{text{ }!!pi!!text{ }}{6}-frac{text{ }!!pi!!text{ }}{3}=-frac{text{ }!!pi!!text{ }}{6}]

Теперь мы окончательно можем посчитать именно ту первообразную, которая нас и интересует:

[Fleft( x right)=text{arctg}x-frac{text{ }!!pi!!text{ }}{6}]

Пример № 2

[fleft( x right)=frac{1}{sqrt{1-{{x}^{2}}}}]

[M=left( frac{1}{2};text{ }!!pi!!text{ } right)]

Здесь также речь идет о тригонометрических функциях. Если мы посмотрим в таблицу, то, действительно, так и получится:

[Fleft( x right)=arcsin x+C]

Нам нужно среди всего множества первообразных найти ту, которая проходит через указанную точку:

[text{ }!!pi!!text{ }=arcsin frac{1}{2}+C]

[text{ }!!pi!!text{ }=frac{text{ }!!pi!!text{ }}{6}+C]

[C=text{ }!!pi!!text{ }-frac{text{ }!!pi!!text{ }}{6}=frac{6text{ }!!pi!!text{ }-text{ }!!pi!!text{ }}{6}=frac{5text{ }!!pi!!text{ }}{6}]

Давайте окончательно запишем:

[Fleft( x right)=arcsin x+frac{5text{ }!!pi!!text{ }}{6}]

Вот так все просто. Единственная проблема состоит в том, для того чтобы считать первообразные простых функций, нужно выучить таблицу первообразных. Однако после изучения таблицы производных для вас, я думаю, это не будет проблемой.

Поэтому идем далее и переходим к более сложным конструкциям — первообразным показательных функций.

Решение задач, содержащих показательную функцию

Для начала запишем такие формулы:

[{{e}^{x}}to {{e}^{x}}]

[{{a}^{x}}to frac{{{a}^{x}}}{ln a}]

Давайте посмотрим, как это все работает на практике.

Пример № 1

[fleft( x right)={{left( {{e}^{x}}+{{e}^{-x}} right)}^{2}}]

Если мы посмотрим на содержимое скобок, то заметим, что в таблице первообразных нет такого выражения, чтобы ${{e}^{x}}$ стояло в квадрате, поэтому этот квадрат необходимо раскрыть. Для этого воспользуемся формулами сокращенного умножения:

[fleft( x right)={{left( {{e}^{x}} right)}^{2}}+2cdot {{e}^{x}}cdot {{e}^{-x}}+{{left( {{e}^{-x}} right)}^{2}}]

[fleft( x right)={{e}^{2x}}+2+{{e}^{-2x}}]

Давайте найдем первообразную для каждого из слагаемых:

[{{e}^{2x}}={{left( {{e}^{2}} right)}^{x}}to frac{{{left( {{e}^{2}} right)}^{x}}}{ln {{e}^{2}}}=frac{{{e}^{2x}}}{2}]

[2to 2x]

[{{e}^{-2x}}={{left( {{e}^{-2}} right)}^{x}}to frac{{{left( {{e}^{-2}} right)}^{x}}}{ln {{e}^{-2}}}=frac{1}{-2{{e}^{2x}}}]

А теперь соберем все слагаемые в единое выражение и получим общую первообразную:

[Fleft( x right)=frac{{{e}^{2x}}}{2}+2x-frac{1}{2{{e}^{2x}}}+C]

Пример № 2

[fleft( x right)={{left( {{2}^{x}}-{{2}^{-x}} right)}^{3}}]

На этот раз степень уже побольше, поэтому формула сокращенного умножения будет довольно сложной. Итак раскроем скобки:

[fleft( x right)={{left( {{2}^{x}} right)}^{3}}-3cdot {{left( {{2}^{x}} right)}^{2}}cdot {{2}^{-x}}+3cdot {{2}^{x}}cdot {{left( {{2}^{-x}} right)}^{2}}-{{left( {{2}^{-x}} right)}^{3}}]

[fleft( x right)={{2}^{3x}}-3cdot {{2}^{x}}+3cdot {{2}^{-x}}-{{2}^{-3x}}]

[fleft( x right)={{8}^{x}}-3cdot {{2}^{x}}+3cdot {{left( frac{1}{2} right)}^{x}}-{{left( frac{1}{8} right)}^{x}}]

Теперь от этой конструкции попробуем взять первообразную от нашей формулы:

[Fleft( x right)=frac{{{8}^{x}}}{ln 8}-3cdot frac{{{2}^{x}}}{ln 2}+3cdot frac{{{left( frac{1}{2} right)}^{x}}}{ln frac{1}{2}}-frac{{{left( frac{1}{8} right)}^{x}}}{ln frac{1}{8}}+C]

[Fleft( x right)=frac{{{8}^{x}}}{ln 8}-frac{3cdot {{2}^{x}}}{ln 2}-frac{3cdot {{left( frac{1}{2} right)}^{x}}}{2}+frac{{{left( frac{1}{8} right)}^{x}}}{3ln 2}+C]

Как видите, в первообразных показательной функции нет ничего сложного и сверхъестественного. Все один считаются через таблицы, однако внимательные ученики наверняка заметят, что первообразная ${{e}^{2x}}$ намного ближе просто к ${{e}^{x}}$ нежели к ${{a}^{x}}$. Так, может быть, существует какой-то более специальное правило, позволяющее, зная первообразную ${{e}^{x}}$, найти ${{e}^{2x}}$? Да, такое правило существует. И, более того, оно является неотъемлемой частью работы с таблицей первообразных. Его мы сейчас разберем на примере тех же самых выражений, с которыми мы только что работали.

Правила работы с таблицей первообразных

Еще раз выпишем нашу функцию:

[fleft( x right)={{left( {{e}^{x}}+{{e}^{-x}} right)}^{2}}={{e}^{2x}}+2+{{e}^{-2x}}]

В предыдущем случае мы использовали для решения следующую формулу:

[{{a}^{x}}to frac{{{a}^{x}}}{operatorname{lna}}]

Но сейчас поступим несколько иначе: вспомним, на каком сновании ${{e}^{x}}to {{e}^{x}}$. Как уже и говорил, потому что производная ${{e}^{x}}$ — это не что иное как ${{e}^{x}}$, поэтому ее первообразная будет равна тому же самому ${{e}^{x}}$. Но проблема в том, что у нас ${{e}^{2x}}$ и ${{e}^{-2x}}$. Сейчас попытаемся найти производную ${{e}^{2x}}$:

[{{left( {{e}^{2x}} right)}^{prime }}={{e}^{2x}}cdot {{left( 2x right)}^{prime }}=2cdot {{e}^{2x}}]

Давайте еще раз перепишем нашу конструкцию:

[{{left( {{e}^{2x}} right)}^{prime }}=2cdot {{e}^{2x}}]

[{{e}^{2x}}={{left( frac{{{e}^{2x}}}{2} right)}^{prime }}]

А это значит, что при нахождении первообразной ${{e}^{2x}}$ мы получим следующее:

[{{e}^{2x}}to frac{{{e}^{2x}}}{2}]

Как видите, мы получили тот же результат, что и ранее, однако не воспользовались формулой для нахождения ${{a}^{x}}$. Сейчас это может показаться глупостью: зачем усложнять вычисления, когда есть стандартная формула? Однако в чуть более сложных выражениях вы убедитесь, что этот прием очень эффективен, т.е. использование производных для нахождения первообразных.

Давайте в качестве разминки аналогичным способом найдем первообразную от ${{e}^{2x}}$:

[{{left( {{e}^{-2x}} right)}^{prime }}={{e}^{-2x}}cdot left( -2 right)]

[{{e}^{-2x}}={{left( frac{{{e}^{-2x}}}{-2} right)}^{prime }}]

При вычислении наша конструкция запишется следующим образом:

[{{e}^{-2x}}to -frac{{{e}^{-2x}}}{2}]

[{{e}^{-2x}}to -frac{1}{2cdot {{e}^{2x}}}]

Мы получили точно тот же результат, но пошли при этом по другому пути. Именно этот путь, который сейчас кажется нам чуть более сложным, в дальнейшем окажется более эффективным для вычисления более сложных первообразных и использование таблиц.

Обратите внимание! Это очень важный момент: первообразные как и производные можно посчитать множеством различных способов. Однако если все вычисления и выкладки будут равны, то ответ получится одним и тем же. Мы убедились в этом только что на примере ${{e}^{-2x}}$ — с одной стороны мы посчитали эту первообразную «напролом», воспользовавшись определением и посчитав ее с помощью преобразований, с другой стороны, мы вспомнили, что ${{e}^{-2x}}$ может быть представлено как ${{left( {{e}^{-2}} right)}^{x}}$ и уже потом воспользовались первообразной для функции ${{a}^{x}}$. Тем не менее, после всех преобразований результат получился одним и тем же, как и предполагалось.

А теперь, когда мы все это поняли, пора перейти к чему-то более существенному. Сейчас мы разберем две простенькие конструкций, однако прием, который будет заложен при их решении, является более мощным и полезным инструментом, нежели простое «беганье» между соседними первообразными из таблицы.

Решение задач: находим первообразную функции

Пример № 1

[fleft( x right)=frac{1=x+{{x}^{2}}}{xsqrt{x}}]

Давайте сумму, которая стоит в числители, разложи на три отдельных дроби:

[fleft( x right)=frac{1}{xsqrt{x}}+frac{x}{xsqrt{x}}+frac{{{x}^{2}}}{xsqrt{x}}]

Это довольно естественный и понятный переход — у большинства учеников проблем с ним не возникает. Перепишем наше выражение следующим образом:

[fleft( x right)=frac{1}{{{x}^{1}}cdot {{x}^{frac{1}{2}}}}+frac{1}{{{x}^{frac{1}{2}}}}+{{x}^{frac{1}{2}}}]

[fleft( x right)={{x}^{-frac{3}{2}}}+{{x}^{-frac{1}{2}}}+{{x}^{frac{1}{2}}}]

А теперь вспомним такую формулу:

[{{x}^{n}}to frac{{{x}^{n+1}}}{n+1}]

В нашем случае мы получим следующее:

[Fleft( x right)=frac{{{x}^{-frac{3}{2}+1}}}{-frac{3}{2}+1}+frac{{{x}^{-frac{1}{2}+1}}}{-frac{1}{2}+1}+frac{{{x}^{frac{1}{2}+1}}}{frac{1}{2}+1}+C]

[Fleft( x right)=frac{{{x}^{-frac{1}{2}}}}{-frac{1}{2}}+frac{{{x}^{frac{1}{2}}}}{frac{1}{2}}+frac{{{x}^{frac{3}{2}}}}{frac{3}{2}}+C]

Чтобы избавиться от всех этих трехэтажных дробей, предлагаю поступить следующим образом:

[Fleft( x right)=frac{-2}{{{x}^{frac{1}{2}}}}+2cdot {{x}^{frac{1}{2}}}+frac{2{{x}^{frac{3}{2}}}}{3}+C]

[Fleft( x right)=-frac{2}{sqrt{x}}+2cdot sqrt{x}+frac{2xsqrt{x}}{3}+C]

Пример № 2

[fleft( x right)=frac{{{x}^{2}}}{{{x}^{2}}+1}]

В отличие от предыдущей дроби в знаменателе стоит не произведение, а сумма. В этом случае мы уже не можем разделить нашу дробь на сумму нескольких простых дробей, а нужно каким-то образом постараться сделать так, чтобы в числителе стояло примерно такое же выражение как в знаменателе. В данном случае сделать это довольно просто:

[fleft( x right)=frac{{{x}^{2}}+1-1}{{{x}^{2}}+1}]

Такая запись, которая на языке математики называется «добавление нуля», позволит нам вновь разделить дробь на два кусочка:

[fleft( x right)=frac{{{x}^{2}}+1}{{{x}^{2}}+1}-frac{1}{{{x}^{2}}+1}]

Теперь найдем то, что искали:

[Fleft( x right)=x-text{arctg}x+C]

Вот и все вычисления. Несмотря на кажущуюся большую сложность, чем в предыдущей задаче, объем вычислений получился даже меньшим.

Нюансы решения

И вот в этом кроется основная сложность работы с табличными первообразными, особенно это заметно на второй задаче. Дело в том, что для того чтобы выделить какие-то элементы, которые легко считаются через таблицу, нам нужно знать, что конкретно мы ищем, и именно в поиске этих элементов и состоит все вычисление первообразных.

Другими словами, недостаточно просто зазубрить таблицу первообразных — нужно уметь видеть что-то, чего пока еще нет, но что подразумевал автор и составитель этой задачи. Именно поэтому многие математики, учителя и профессора постоянно спорят: «А что такое взятие первообразных или интегрирование — это просто инструмент либо это настоящее искусство?» На самом деле, лично на мой взгляд, интегрирование — это никакое не искусство — в нем нет ничего возвышенного, это просто практика и еще раз практика. И чтобы попрактиковаться, давайте решим еще три более серьезных примера.

Тренируемся в интегрировании на практике

Задача № 1

[fleft( x right)=frac{{{x}^{4}}}{{{x}^{2}}+1}]

Запишем такие формулы:

[{{x}^{n}}to frac{{{x}^{n+1}}}{n+1}]

[frac{1}{x}to ln x]

[frac{1}{1+{{x}^{2}}}to text{arctg}x]

Давайте запишем следующее:

[fleft( x right)=frac{{{x}^{4}}+{{x}^{2}}}{{{x}^{2}}+1}-frac{{{x}^{2}}}{{{x}^{2}}+1}]

[fleft( x right)=frac{{{x}^{2}}left( {{x}^{2}}+1 right)}{{{x}^{2}}+1}-frac{{{x}^{2}}+1-1}{{{x}^{2}}+1}]

[fleft( x right)={{x}^{2}}-1+frac{1}{{{x}^{2}}+1}]

[Fleft( x right)=frac{{{x}^{3}}}{3}-x+3+text{arctg}x+C]

Задача № 2

[fleft( x right)=frac{2{{x}^{2}}-3}{{{x}^{2}}+1}]

Перепишем следующим образом:

[fleft( x right)=frac{2{{x}^{2}}+2-2-3}{{{x}^{2}}+1}]

[fleft( x right)=frac{2{{x}^{2}}+2}{{{x}^{2}}+1}-frac{5}{{{x}^{2}}+1}]

[fleft( x right)=frac{2left( {{x}^{2}}+1 right)}{{{x}^{2}}+1}-frac{5}{{{x}^{2}}+1}]

Итого первообразная будет равна:

[Fleft( x right)=2x-5text{arctg}x+C]

Задача № 3

[fleft( x right)=frac{1}{{{x}^{2}}left( 1+{{x}^{2}} right)}]

Сложность этой задачи состоит в том, что в отличие от предыдущих функций сверху вообще отсутствует какая-либо переменная $x$, т.е. нам непонятно, что добавлять, вычитать, чтобы получить хоть что-то похожее на то, что стоит снизу. Однако, на самом деле, это выражение считается даже проще, чем любое выражение из предыдущих конструкций, потому что данную функцию можно переписать следующим образом:

[fleft( x right)=frac{1}{{{x}^{2}}}-frac{1}{{{x}^{2}}+1}]

Возможно, вы сейчас спросите: а почему эти функции равны? Давайте проверим:

[fleft( x right)=frac{1}{{{x}^{2}}}-frac{1}{{{x}^{2}}+1}=frac{{{x}^{2}}+1-{{x}^{2}}}{{{x}^{2}}left( {{x}^{2}}+1 right)}=frac{1}{{{x}^{2}}left( {{x}^{2}}+1 right)}]

Еще перепишем:

[fleft( x right)={{x}^{-2}}-frac{1}{{{x}^{2}}+1}]

Найдем:

[Fleft( x right)=frac{{{x}^{-1}}}{-1}-text{arctg}x+C]

Немного преобразуем наше выражение:

[Fleft( x right)=-frac{1}{x}-text{arctg}x+C]

И когда я все это объясняю своим ученикам, практически всегда возникает одна и та же проблема: с первой функцией все более-менее понятно, со второй тоже при везении или практике можно разобраться, но каким альтернативным сознанием нужно обладать, чтобы решить третий пример? На самом деле, не пугайтесь. Тот прием, который мы использовали при вычислении последней первообразной, называется «разложение функции на простейшие», и это очень серьезный прием, и ему будет посвящен отдельный видеоурок.

А пока предлагаю вернуться к тому, что мы только что изучили, а именно, к показательным функциям и несколько усложнить задачи с их содержанием.

Более сложные задачи на решение первообразных показательных функций

Задача № 1

[fleft( x right)={{2}^{x}}cdot {{5}^{x}}]

Заметим следующее:

[{{2}^{x}}cdot {{5}^{x}}={{left( 2cdot 5 right)}^{x}}={{10}^{x}}]

[fleft( x right)={{10}^{x}}]

Чтобы найти первообразной этого выражения, достаточно просто воспользоваться стандартной формулой — ${{a}^{x}}to frac{{{a}^{x}}}{ln a}$.

В нашем случае первообразная будет такая:

[Fleft( x right)=frac{{{10}^{x}}}{ln 10}+C]

Разумеется, на фоне той конструкции, которую мы решали только что, эта выглядит более простой.

Задача № 2

[fleft( x right)=frac{{{8}^{x}}-{{9}^{x}}}{{{6}^{x}}}]

Опять же, несложно заметить, что эту функцию несложно разделить на два отдельных слагаемых — две отдельных дроби. Перепишем:

[fleft( x right)=frac{{{8}^{x}}}{{{6}^{x}}}-frac{{{9}^{x}}}{{{6}^{x}}}={{left( frac{8}{6} right)}^{x}}-{{left( frac{9}{6} right)}^{x}}={{left( frac{4}{3} right)}^{x}}-{{left( frac{3}{2} right)}^{x}}]

Осталось найти первообразную от каждого от этих слагаемых по вышеописанной формуле:

[Fleft( x right)frac{{{left( frac{4}{3} right)}^{x}}}{ln frac{4}{3}}-frac{{{left( frac{3}{2} right)}^{x}}}{ln frac{3}{2}}+C]

Несмотря на кажущуюся большую сложность показательных функций по сравнению со степенными, общий объем вычислений и выкладок получился гораздо проще.

Конечно, для знающих учеников то, что мы только что разобрали (особенно на фоне того, что мы разобрали до этого), может показаться элементарными выражениями. Однако выбирая именно две эти задачи для сегодняшнего видеоурока, я не ставил себе цель рассказать вам еще один сложный и навороченный прием — все, что я хотел вам показать, так это то, что не стоит бояться использовать стандартные приемы алгебры для преобразования исходных функций.

Использование «секретного» приема

В заключение хотелось бы разобрать еще один интересный прием, который, с одной стороны выходит за рамки того, что мы сегодня в основном разбирали, но, с другой стороны, он, во-первых, отнюдь не сложный, т.е. его могут освоить даже начинающие ученики, а, во-вторых, он довольно часто встречается на всевозможных контрольных и самостоятельных работах, т.е. знание его будет очень полезно в дополнение к знанию таблицы первообразных.

Задача № 1

[fleft( x right)={{left( x-5 right)}^{4}}]

Очевидно, что перед нами что-то очень похожее на степенную функцию. Как нам поступить в этом случае? Давайте задумаемся: $x-5$ отличается от $x$ не так уж и сильно — просто добавили $-5$. Запишем так:

[{{x}^{4}}to frac{{{x}^{5}}}{5}]

[{{left( frac{{{x}^{5}}}{5} right)}^{prime }}=frac{5cdot {{x}^{4}}}{5}={{x}^{4}}]

Давайте попробуем найти производную от ${{left( x-5 right)}^{5}}$:

[{{left( {{left( x-5 right)}^{5}} right)}^{prime }}=5cdot {{left( x-5 right)}^{4}}cdot {{left( x-5 right)}^{prime }}=5cdot {{left( x-5 right)}^{4}}]

Отсюда следует:

[{{left( x-5 right)}^{4}}={{left( frac{{{left( x-5 right)}^{5}}}{5} right)}^{prime }}]

В таблице нет такого значения, поэтому мы сейчас сами вывели эту формулу, используя стандартную формулу первообразной для степенной функции. Давайте так и запишем ответ:

[Fleft( x right)=frac{{{left( x-5 right)}^{5}}}{5}+C]

Задача № 2

[fleft( x right)={{left( 4-3x right)}^{9}}]

Многим ученикам, которые посмотрят на первое решение, может показаться, что все очень просто: достаточно заменить в степенной функции $x$ на линейное выражение, и все станет на свои места. К сожалению, все не так просто, и сейчас мы в этом убедимся.

По аналогии с первым выражением запишем следующее:

[{{x}^{9}}to frac{{{x}^{10}}}{10}]

[{{left( {{left( 4-3x right)}^{10}} right)}^{prime }}=10cdot {{left( 4-3x right)}^{9}}cdot {{left( 4-3x right)}^{prime }}=]

[=10cdot {{left( 4-3x right)}^{9}}cdot left( -3 right)=-30cdot {{left( 4-3x right)}^{9}}]

Возвращаясь к нашей производной, мы можем записать:

[{{left( {{left( 4-3x right)}^{10}} right)}^{prime }}=-30cdot {{left( 4-3x right)}^{9}}]

[{{left( 4-3x right)}^{9}}={{left( frac{{{left( 4-3x right)}^{10}}}{-30} right)}^{prime }}]

Отсюда сразу следует:

[Fleft( x right)=frac{{{left( 4-3x right)}^{10}}}{-30}+C]

Нюансы решения

Обратите внимание: если в прошлый раз по сути ничего не поменялось, то во втором случае вместо $-10$ появилось $-30$. На что отличается $-10$ и $-30$? Очевидно, что на множитель $-3$. Вопрос: откуда он взялся? Присмотревшись можно увидеть, что она взялась в результате вычислений производной сложной функции — тот коэффициент, который стоял при $x$, появляется в первообразной внизу. Это очень важное правило, которое я изначально вообще не планировал разбирать в сегодняшнем видеоуроке, но без него изложение табличных первообразных было бы неполным.

Итак, давайте еще раз. Пусть есть наша основная степенная функция:

[{{x}^{n}}to frac{{{x}^{n+1}}}{n+1}]

А теперь вместо $x$ давайте подставим выражение $kx+b$. Что тогда произойдет? Нам нужно найти следующее:

[{{left( kx+b right)}^{n}}to frac{{{left( kx+b right)}^{n+1}}}{left( n+1 right)cdot k}]

На каком основании мы это утверждаем? Очень просто. Давайте найдем производную написанной выше конструкции:

[{{left( frac{{{left( kx+b right)}^{n+1}}}{left( n+1 right)cdot k} right)}^{prime }}=frac{1}{left( n+1 right)cdot k}cdot left( n+1 right)cdot {{left( kx+b right)}^{n}}cdot k={{left( kx+b right)}^{n}}]

Это то самое выражение, которое изначально и было. Таким образом, эта формула тоже верна, и ею можно дополнить таблицу первообразных, а лучше просто запомнить всю таблицу.

Выводы из «секретного: приема:

• Обе функции, которые мы только что рассмотрели, на самом деле, могут быть сведены к первообразным, указанным в таблице, путем раскрытия степеней, но если с четвертой степенью мы еще более-менее как-то справимся, то вот девятую степень я бы вообще не рискнул раскрывать.
• Если бы мы раскрыли степени, то мы бы получили такой объем вычислений, что простая задача заняла бы у нас неадекватно большое количество времени.
• Именно поэтому такие задачи, внутри которых стоят линейные выражения, не нужно решать «напролом». Как только вы встречаете первообразную, которая отличается от той, что в таблице, лишь наличием выражения $kx+b$ внутри, сразу вспоминайте написанную выше формулу, подставляйте ее в вашу табличную первообразную, и все у вас получится намного быстрее и проще.

Естественно, в силу сложности и серьезности этого приема мы еще неоднократно вернемся к его рассмотрению в будущих видеоуроках, но на сегодня у меня все. Надеюсь, этот урок действительно поможет тем ученикам, которые хотят разобраться в первообразных и в интегрировании.

До новых встреч!

Смотрите также:

1. Первообразная функции
2. Интегрирование по частям
3. Решение задач B12: №448—455
4. Что такое ЕГЭ по математике 2011 и как его сдавать
5. Материалы для подготовки к ЕГЭ по математике
6. Нестандартная задача B2: студенты, гонорары и налоги

Первообра́зная. Красивое слово.) Для начала немного русского
языка. Произносится это слово именно так, а не «первоОбразная»,
как может показаться. Первообразная — базовое понятие всего интегрального
исчисления. Любые интегралы — неопределённые, определённые (с ними вы
познакомитесь уже в этом семестре), а также двойные, тройные, криволинейные,
поверхностные (а это уже главные герои второго курса) — строятся на этом
ключевом понятии. Имеет полный смысл освоить. Поехали.)

        Прежде чем знакомиться
с понятием первообразной, давайте в самых общих чертах вспомним самую
обычную производную. Не углубляясь в занудную теорию пределов,
приращений аргумента и прочего, можно сказать, что нахождение производной
(или дифференцирование) — это просто математическая операция
над функцией. И всё. Берётся любая функция (допустим, f(x)
= x²) и по определённым
правилам преобразовывается, превращаясь в новую функцию. И
вот эта самая новая функция и называется производной.

        В нашем случае, до дифференцирования
была функция f(x) = x²,
а после дифференцирования стала уже другая функция f’(x) =
2x.

        Производная —
потому, что наша новая функция f’(x) = 2x произошла от
функции f(x) = x². В
результате операции дифференцирования. И причём именно от неё, а не от какой-то
другой функции (x³,
например).

        Грубо говоря, f(x) = x² —
это мама, а f’(x) = 2x — её любимая дочка.) Это понятно. Идём
дальше.

        Математики — народ
неугомонный. На каждое своё действие стремятся найти противодействие. Есть
сложение — есть и вычитание. Есть умножение — есть и деление.
Возведение в степень — извлечение корня. Синус — арксинус. Точно
также есть дифференцирование – значит, есть и… интегрирование.)

        А теперь поставим такую
интересную задачу. Есть у нас, допустим, такая простенькая функция f(x)
= 1. И нам надо ответить на такой вопрос:

        Производная КАКОЙ функции даёт нам
функцию f(x) = 1?

        Иными словами, видя дочку, с помощью
анализа ДНК, вычислить, кто же её мамаша. Так от какой же исходной функции
(назовём её F(x)) произошла наша производная функция f(x) = 1?
Или, в математической форме, для какой функции F(x)
выполняется равенство: 

        F’(x) = f(x) = 1?

        Пример элементарный. Я
старался.) Просто подбираем функцию F(x) так, чтобы равенство сработало. Ну
как, подобрали? Да, конечно! F(x) = x. Потому, что:

        F’(x) = x’ = 1 = f(x).

        Разумеется, найденную
мамочку F(x) = x надо как-то назвать, да.) Знакомьтесь!

        Первообразной
для функции f(x) называется такая функция F(x), производная которой
равна f(x), т.е. для которой справедливо равенство F’(x) = f(x).

        Вот и всё. Больше
никаких научных хитростей. В строгом определении добавляется ещё дополнительная
фраза «на промежутке Х». Но мы пока в эти тонкости
углубляться не будем, ибо наша первоочередная задача — научиться находить
эти самые первообразные.

        В нашем случае как раз и получается,
что функция F(x) = x является первообразной для
функции f(x) = 1.

        Почему? Потому что F’(x) =
f(x) = 1. Производная икса есть единица. Возражений нет.)

        Термин «первообразная»
по-обывательски означает «родоначальница», «родитель»,
«предок». Сразу же вспоминаем самого родного и близкого человека.) А
сам поиск первообразной — это восстановление исходной функции по
известной её производной. Иными словами, это действие, обратное
дифференцированию. И всё! Сам же этот увлекательный процесс тоже называется
вполне научно — интегрирование. Но об интегралах —
позже. Терпение, друзья!)

        Запоминаем: 

        Интегрирование —
это математическая операция над функцией (как и дифференцирование).

        Интегрирование — операция,
обратная дифференцированию.

        Первообразная — результат
интегрирования.

        А теперь усложним задачу. Найдём
теперь первообразную для функции f(x) = x. То есть, найдём такую
функцию F(x), чтобы её производная равнялась
бы иксу:

        F’(x) = x

        Кто дружит с производными, тому, возможно,
на ум придёт что-то типа:

        (x²)’
= 2x.

        Что ж, респект и уважуха тем, кто
помнит таблицу производных!) Верно. Но есть одна проблемка. Наша исходная
функция f(x) = x, а (x²)’
= 2x. Два икс. А у нас
после дифференцирования должен получиться просто икс. Не катит. Но…

        Мы с вами народ учёный. Аттестаты
получили.) И со школы знаем, что обе части любого равенства можно умножать и
делить на одно и то же число (кроме нуля, разумеется)! Так уж тождественные
преобразования устроены. Вот и реализуем
эту возможность себе во благо.)

        Мы ведь хотим, чтобы справа
остался чистый икс, верно? А двойка мешает… Вот и берём соотношение
для производной (x²)’ = 2x и
делим обе его части на эту самую двойку:

        Так, уже кое-чего проясняется. Идём
дальше. Мы знаем, что любую константу можно вынести за знак
производной. Вот так:

        Все формулы в математике работают как
слева направо, так и наоборот — справа налево. Это значит, что, с тем
же успехом, любую константу можно и внести под знак производной:

        В нашем случае спрячем двойку в
знаменателе (или, что то же самое, коэффициент 1/2) под знак производной:

        А теперь внимательно присмотримся
к нашей записи. Что мы видим? Мы видим равенство, гласящее, что производная
от чего-то (это что-то — в скобочках)
равняется иксу.         

        Полученное равенство как раз и
означает, что искомой первообразной для функции f(x) = x служит
функция F(x) = x²/2.
Та, что стоит в скобочках под штрихом. Прямо по смыслу первообразной.) Что ж,
проверим результат. Найдём производную:

        

        Отлично! Получена исходная
функция f(x) = x. От чего плясали, к тому и вернулись. Это значит,
что наша первообразная найдена верно.)

        А если f(x) = x²?
Чему равна её первообразная? Не вопрос! Мы с вами знаем (опять же, из правил дифференцирования),
что:

        3x² =
(x³)’

        И, стало
быть,

        

        Уловили? Теперь мы, незаметно для
себя, научились считать первообразные для любой степенной функции
f(x)=xⁿ. В уме.) Берём исходный
показатель n, увеличиваем его на единичку, а в качестве компенсации
делим всю конструкцию на n+1:

        Полученная формулка, между прочим,
справедлива не только для натурального показателя степени n,
но и для любого другого — отрицательного, дробного. Это позволяет легко
находить первообразные от простеньких дробей и корней.

        Например:

        

        

        Естественно, n ≠ -1 ,
иначе в знаменателе формулы получается ноль, и формула теряет смысл.) Про
этот особый случай n = -1 чуть позже.)

Что такое неопределённый
интеграл? Таблица интегралов.

        Идём дальше. Те студенты, которые хотя
бы мало-мальски «шарят» в производных, — люди грамотные. И,
возможно, уже приготовили мне убойный вопрос.

        Скажем, чему равна производная для
функции F(x) = x? Ну, единица, единица — слышу
недовольные ответы… Всё верно. Единица. Но… Для функции G(x) = x+1 производная тоже
будет равна единице:

        

        Также производная будет равна единице
и для функции x+1234, и для функции x-10, и
для любой другой функции вида x+C, где С —
любая константа. Ибо производная любой константы равна нулю, а от прибавления/вычитания
нуля никому ни холодно ни жарко.)

        Получается неоднозначность. Выходит,
что для функции f(x) = 1 первообразной служит не
только функция F(x) = x, но и функция  F₁(x)
= x+1234 и функция F₂(x)
= x-10 и так далее!

        Да. Именно так.) У всякой (непрерывной
на промежутке) функции существует не какая-то одна первообразная,
а бесконечно много — целое семейство! Не одна мама или
папа, а целая родословная, ага.)

        Но! Всех наших
родственников-первообразных объединяет одно важное свойство. На то они и
родственники.) Свойство настолько важное, что в процессе разбора приёмов
интегрирования мы про него ещё не раз вспомним. И будем вспоминать ещё
долго.) 

        Вот оно, это свойство:

        Любые две
первообразные F₁(x)
и F₂(x) от
одной и той же функции f(x) отличаются на константу:

        F₁(x)
— F₂(x) = С.

        Кому интересно доказательство —
штудируйте литературу или конспекты лекций.) Ладно, так уж и быть, докажу.
Благо доказательство тут элементарное, в одно действие. Берём равенство

        F₁(x)
— F₂(x) = С

        и дифференцируем
обе его части. То есть, просто тупо ставим штрихи:

        Вот и всё. Как говорится, ЧТД.

        О чём говорит это свойство? А о том,
что две различные первообразные от одной и той же функции f(x) не
могут отличаться на какое-то выражение с иксом . Только
строго на константу! Иными словами, если у нас есть график какой-то одной
из первообразных (пусть это будет F(x)), то графики всех
остальных наших первообразных строятся параллельным переносом графика
F(x) вдоль оси игреков.

        Посмотрим, как это выглядит на примере
функции f(x) = x. Все её первообразные, как нам уже известно, имеют
общий вид F(x) = x²/2+C.
На картинке это выглядит как бесконечное множество парабол,
получаемых из «основной» параболы y = x²/2 сдвигом
вдоль оси OY вверх или вниз в зависимости от значения константы С.

        Помните школьное построение графика
функции y=f(x)+a сдвигом графика y=f(x) на
«а» единиц вдоль оси игреков?) Вот и тут то же самое.)

        Причём, обратите внимание: наши
параболы нигде не пересекаются! Оно и естественно. Ведь две
различные функции y₁(x) и y₂(x)
неизбежно будут соответствовать двум различным значениям константы — С₁ и С₂.

        Поэтому уравнение y₁(x)
= y₂(x) никогда не имеет решений:

С₁ =
С₂

x ∊ ∅,
так как С₁ ≠
С2

        А теперь мы плавненько подходим ко
второму краеугольному понятию интегрального исчисления. Как мы только что
установили, у всякой функции f(x) существует бесконечное множество
первообразных F(x) + C, отличающихся друг от друга на константу. Это самое
бесконечное множество тоже имеет своё специальное название.) Что ж, прошу
любить и жаловать!

        Что такое
неопределённый интеграл?

        Множество
всех первообразных для функции f(x) называется неопределённым
интегралом от функции f(x).

        Вот и всё
определение.)

        «Неопределённый» —
потому, что множество всех первообразных для одной и той же функции бесконечно.
Слишком много различных вариантов.)

        «Интеграл» —
с подробной расшифровкой этого зверского слова мы познакомимся в следующем
большом разделе, посвящённом определённым интегралам. А пока, в
грубой форме, будем считать интегралом нечто общее, единое, целое.
А интегрированием — объединение, обобщение, в
данном случае переход от частного (производной) к общему (первообразным). Вот,
как-то так.

        Обозначается неопределённый интеграл
вот так:

        Читается так же, как и пишется: интеграл
эф от икс дэ икс. Или интеграл от эф от икс дэ
икс. Ну, вы поняли.)

        Теперь разберёмся с обозначениями.

        ∫ — значок
интеграла. Смысл тот же, что и штрих для производной.)

        d — значок дифференциала. Не
пугаемся! Зачем он там нужен — чуть ниже.

        f(x) — подынтегральная
функция (через «ы»).

        f(x)dx — подынтегральное
выражение. Или, грубо говоря, «начинка» интеграла.

        Согласно смыслу неопределённого
интеграла,

        Здесь F(x) — та
самая первообразная для функции f(x), которую мы
так или иначе нашли сами. Как именно нашли — не
суть. Например, мы установили, что F(x) = x²/2 для f(x)=x.

        «С» — произвольная
постоянная. Или, более научно, интегральная константа.
Или константа интегрирования. Всё едино.)

        А теперь вернёмся к нашим самым первым
примерам на поиск первообразной. В терминах неопределённого интеграла можно
теперь смело записать:

        

        

        

        

        

        И так далее.) Идея понятна, думаю. Ни
в коем случае не забываем приплюсовывать константу С!

Что такое интегральная константа
и зачем она нужна?

        Вопрос очень интересный. И очень
(ОЧЕНЬ!) важный. Интегральная константа из всего бесконечного множества
первообразных выделяет ту линию, которая проходит через заданную точку.

         В чём суть.
Из исходного бесконечного множества первообразных (т.е. неопределённого
интеграла) надо выделить ту кривую, которая будет проходить через
заданную точку. С какими-то конкретными координатами. Такое
задание всегда и везде встречается при начальном знакомстве с интегралами.
Как в школе, так и в ВУЗЕ.

         Типичная задачка:

         Среди множества всех
первообразных функции f=x выделить ту, которая проходит через точку (2;2).

         Начинаем
думать головой… Множество всех первоообразных  — это значит,
сначала надо проинтегрировать нашу исходную функцию. То
есть, икс (х). Этим мы занимались чуть выше и получили такой ответ:

         

         А теперь разбираемся, что именно
мы получили. Мы получили не одну функцию, а целое семейство функций. Каких
именно? Вида y=x²/2+C. Зависящее
от значения константы С. И вот это значение константы нам и предстоит
теперь «отловить».) Ну что, займёмся ловлей?)

         Удочка наша — семейство
кривых (парабол) y=x²/2+C. 

         Константы — это
рыбины. Много-много. Но на каждую найдётся свой крючок и приманка.)

         А что же
служит приманкой? Правильно! Наша точка (-2;2).

         Вот и
подставляем координаты нашей точки в общий вид первообразных! Получим:

         

         y(2) = 2

         

         Отсюда уже легко ищется C
= 0.         

         Что сиё означает? Это значит,
что из всего бесконечного множества парабол вида y=x²/2+C только парабола
с константой С=0 нам подходит! А именно: y=x²/2. И
только она. Только эта парабола будет проходить через нужную
нам точку (-2; 2). А все остальные параболы из нашего
семейства проходить через эту
точку уже не будут. Через какие-то другие точки
плоскости — да, а вот через точку (2; 2) — уже нет. Уловили?

         Для наглядности вот вам две
картинки — всё семейство парабол (т.е. неопределённый интеграл) и
какая-то конкретная парабола, соответствующая конкретному
значению константы и проходящая через конкретную точку:

        Видите, насколько важно учитывать
константу С при интегрировании! Так что не пренебрегаем этой
буковкой «С» и не забываем приписывать к окончательному ответу.

        А теперь разберёмся, зачем же внутри
интегралов везде тусуется символ dx. Забывают про него
студенты частенько… А это, между прочим, тоже ошибка! И довольно грубая. Всё
дело в том, что интегрирование — операция, обратная дифференцированию. А
что именно является результатом дифференцирования? Производная?
Верно, но не совсем. Дифференциал!

        В нашем случае, для функции f(x) дифференциал её
первообразной F(x), будет:

        

        Кому непонятна данная цепочка —
срочно повторить определение и смысл дифференциала и то, как именно он
раскрывается! Иначе в интегралах будете тормозить нещадно….

        Напомню, в самой грубой обывательской
форме, что дифференциал любой функции f(x) — это просто произведение f’(x)dx.
И всё! Взять производную и помножить её на дифференциал аргумента (т.е.
dx). То есть, любой дифференциал, по сути, сводится к вычислению обычной производной.

        Поэтому, строго говоря, интеграл
«берётся» не от функции f(x), как принято
считать, а от дифференциала f(x)dx! Но, в
упрощённом варианте, принято говорить, что «интеграл берётся от
функции». Или: «Интегрируется функция f(x)«. Это
одно и то же. И мы будем говорить точно так же. Но про значок dx при
этом забывать не будем!

        И сейчас я подскажу, как его не забыть
при записи. Представьте себе сначала, что вы вычисляете обычную производную по
переменной икс. Как вы обычно её пишете?

        Вот так: f’(x), y’(x), у’_x.
Или более солидно, через отношение дифференциалов: dy/dx. Все эти записи нам
показывают, что производная берётся именно по иксу. А не по «игреку»,
«тэ» или какой-то там другой переменной.)

        Так же и в интегралах. Запись ∫f(x)dx нам
тоже как бы показывает, что интегрирование проводится
именно по переменной икс. Конечно, это всё очень упрощённо и
грубо, но зато понятно, я надеюсь. И шансы забыть приписать
вездесущее dx резко снижаются.)

        Итак, что такое же неопределённый
интеграл — разобрались. Прекрасно.) Теперь хорошо бы научиться эти самые
неопределённые интегралы вычислять. Или, попросту говоря,
«брать». И вот тут студентов поджидает две новости — хорошая
и не очень. Пока начнём с хорошей.)

         Новость хорошая. Для интегралов,
так же как и для производных, существует своя табличка. И все интегралы,
которые нам будут встречаться по пути, даже самые страшные и навороченные,
мы по определённым правилам будем так или иначе сводить к этим
самым табличным.)

        Итак, вот она, таблица
интегралов!

        Вот такая вот красивая табличка
интегралов от самых-самых популярных функций. Рекомендую обратить отдельное
внимание на группу формул 1-2 (константа и степенная функция). Это — самые
употребительные формулы в интегралах!

        Третья группа формул (тригонометрия),
как можно догадаться, получена простым обращением соответствующих формул для
производных.

        Например:

         
 

        C четвёртой группой формул
(показательная функция) — всё аналогично.

        А вот четыре последние группы формул
(5-8) для нас новые. Откуда же они взялись и за какие такие
заслуги именно эти экзотические функции, вдруг, вошли в таблицу основных
интегралов? Чем же эти группы функций так выделяются на фоне остальных функций?

        Так уж сложилось исторически в
процессе развития методов интегрирования. Когда мы будем
тренироваться брать самые-самые разнообразные интегралы, то вы поймёте, что
интегралы от перечисленных в таблице функций встречаются очень и очень часто.
Настолько часто, что математики отнесли их к табличным.) Через них выражаются
очень многие другие интегралы, от более сложных конструкций.

        Ради интереса можно взять какую-нибудь
из этих жутких формул и продифференцировать. Например, самую зверскую 7-ю
формулу.

        

        

        Всё нормально. Не обманули математики.

        Таблицу интегралов, как и таблицу
производных, желательно знать наизусть. Во всяком случае, первые четыре группы
формул. Это не так трудно, как кажется на первый взгляд. Заучивать наизусть
последние четыре группы (с дробями и корнями) пока не стоит.
Всё равно поначалу будете путаться, где логарифм писать, где арктангенс,
где арксинус, где 1/а, где 1/2а … Выход тут один — решать побольше примеров.
Тогда таблица сама собой постепенно и запомнится, а сомнения грызть
перестанут.)

        Особо любознательные лица,
присмотревшись к таблице, могут спросить: а где же в таблице интегралы от
других элементарных «школьных» функций — тангенса, логарифма,
«арков»? Скажем, почему в таблице ЕСТЬ интеграл от синуса, но при
этом НЕТУ, скажем, интеграла от тангенса tg x? Или нету интеграла
от логарифма ln x? От арксинуса arcsin x? Чем они хуже?
Но зато полно каких-то «левых» функций — с корнями, дробями,
квадратами…

        Ответ. Ничем не хуже.) Просто
вышеназванные интегралы (от тангенса, логарифма, арксинуса и т.д.) не
являются табличными. И встречаются на практике значительно реже, нежели
те, что представлены в таблице. Поэтому знать наизусть, чему они
равны, вовсе не обязательно. Достаточно лишь знать, как они вычисляются.)

        Что, кому-то всё-таки невтерпёж? Так
уж и быть, специально для вас!

        Ну как, будете заучивать? Не
будете? И не надо.) Но не волнуйтесь, все подобные интегралы мы обязательно
найдём. В соответствующих уроках.

        Что ж, теперь переходим к свойствам
неопределённого интеграла. Да-да, ничего не поделать! Вводится новое
понятие — тут же и какие-то его свойства рассматриваются.

Свойства неопределённого
интеграла.

        Теперь не очень хорошая новость.

        В отличие от дифференцирования, общих
стандартных правил интегрирования, справедливых на все случаи жизни,
в математике нету. Это фантастика!

        Например, вы все прекрасно знаете
(надеюсь!), что любое произведение любых двух
функций f(x)·g(x) дифференцируется вот так:

(f(x)·g(x))’ = f’(x)·g(x) +
f(x)·g’(x).

        Любое частное
дифференцируется вот так:

        А любая сложная функция, какой бы накрученной
она ни была, дифференцируется вот так:

        И какие бы функции ни скрывались под
буквами f и g, общие правила всё равно сработают и производная, так или иначе,
будет найдена.

        А вот с интегралами такой номер уже не
пройдёт: для произведения, частного (дроби), а также сложной функции общих
формул интегрирования не существует! Нету никаких
стандартных правил! Вернее, они есть. Это я зря математику обидел.)
Но, во-первых, их гораздо меньше, чем общих правил для дифференцирования. А
во-вторых, большинство методов интегрирования, о которых мы будем разговаривать
в следующих уроках, очень и очень специфические. И справедливы лишь для
определённого, очень ограниченного класса функций. Скажем, только для дробно-рациональных
функций. Или каких-то ещё.

        А какие-то интегралы, хоть и
существуют в природе, но вообще никак не выражаются через элементарные
«школьные» функции! Да-да, и таких интегралов полно!

        Именно поэтому интегрирование —
гораздо более трудоёмкое и кропотливое занятие, чем дифференцирование. Но в
этом есть и своя изюминка. Занятие это творческое и очень увлекательное.) И,
если вы хорошо усвоите таблицу интегралов и освоите хотя бы два базовых приёма,
о которых мы поговорим далее (замена
переменной и интегрирование
по частям), то интегрирование вам очень понравится.

        А теперь познакомимся, собственно, со
свойствами неопределённого интеграла. Их всего ничего. Вот они.

        Первые два свойства полностью
аналогичны таким же свойствам для производных и называются свойствами
линейности неопределённого интеграла. Тут всё просто и логично:
интеграл от суммы/разности равен сумме/разности интегралов, а постоянный
множитель можно вынести за знак интеграла.

        А вот следующие три свойства для нас
принципиально новые. Разберём их поподробнее. Звучат по-русски они следующим
образом.

        Третье свойство

        Производная
от интеграла равна подынтегральной функции

        Всё просто, как в сказке. Если
проинтегрировать функцию, а потом обратно найти производную от результата, то…
получится исходная подынтегральная функция. Этим свойством всегда можно (и
нужно) пользоваться для проверки окончательного результата интегрирования.
Вычислили интеграл — продифференцируйте ответ! Получили подынтегральную
функцию — ОК. Не получили — значит, где-то накосячили. Ищите ошибку.)

        Конечно же, в ответе могут получаться
настолько зверские и громоздкие функции, что и обратно дифференцировать их
неохота, да. Но лучше, по возможности, стараться себя проверять. Хотя бы в тех
примерах, где это несложно.)

        Идём дальше, по порядочку.

        Четвёртое свойство

        Дифференциал
от интеграла равен подынтегральному выражению.

        Тут ничего особенного. Суть та же
самая, только dx на конце появляется. Согласно предыдущему свойству и правилам
раскрытия дифференциала.

        Пятое свойство

        Интеграл
от дифференциала некоторой функции равен сумме этой функции и произвольной
постоянной.

        Тоже очень простое свойство. Им мы
тоже будем регулярно пользоваться в процессе решения интегралов.
Особенно — в методе
подведения функции под знак дифференциала и замены
переменной.

        Вот такие вот полезные свойства.
Занудствовать с их строгими доказательствами я здесь не собираюсь. Желающим
предлагаю это сделать самостоятельно. Прямо по смыслу производной и
дифференциала. Докажу лишь последнее, пятое свойство, ибо оно менее очевидно.

        Итак, у нас есть утверждение:

           

        Вытаскиваем
«начинку» нашего интеграла и раскрываем, согласно определению
дифференциала:

           

        На всякий случай, напоминаю, что,
согласно нашим обозначениям производной и первообразной, F’(x)
= f(x).

        Вставляем теперь наш результат обратно
внутрь интеграла:

           

        Получено в точности определение
неопределённого интеграла (да простит меня русский язык)!

        Вот и всё.)