Примеры на интегрирование функций подобного состава заданий задают студентам 1, 2 курсов. Это в основном задания для математиков, экономистов, статистов, программистов. Данные интегралы задавали на контрольной работе в ЛНУ им. И. Франка, другие ВУЗы Украины также практикует подобные здания на контрольных по интегрированию. Чтобы формулы в задачах и ответах не повторялись условия заданий выписывать не будем. Всем и так известно что в задачах нужно или «Найти интеграл», или «Вычислить интеграл».
Пример 18. Для раскрытия иррациональности в знаменателе дроби необходимо в подобных примерах выполнять такую замену переменных — «икс» в наименьшей степени. В результате придем к интегралу от дробной функции
дальше выполняем деления числителя на знаменатель и упрощение
Таким образом без громоздких расписаний дробей придем к интегралу
Пример 19. Корневую функцию обозначаем за новую переменную в квадрате (для удобства вычислений). Далее находим дифференциал переменной, подставляем в неопределенный интеграл и выполняем упрощение.
В результате замены получим дробь которая разделяется на два интеграла. Второй интеграл равен разнице логарифмов
Пример 20. Следующие интегралы касаются исключительно тригонометрических функций, а именно их произведения, квадратов, кубов, рациональных функций. Первый из приведенных интегралов нужно свести к синусу. Для этого косинус в 5 степени расписываем на произведение косинуса в 4 степени на косинус, который вносим под дифференциал
Для упрощения вводим замену переменных и приходим к интегрированию полинома
После интегрирования возвращаемся к замене и вместо t везде записываем sin(x).
Пример 21. Для вычисления интеграла нужно снизить степень синуса. Таким образом используем тригонометрические формулы, понижаем степень первой, а дальше находим интеграл по табличным формулам.
Пример 22. Нужно найти интеграл от произведения двойного синуса на тройной косинус. Под дифференциал ничего внести не удастся, поскольку имеем различные переменные. Для упрощения распишем произведение тригонометрических функций через разницу синусов
Пример 23. Данный интеграл без универсальной тригонометрической замены переменных найти не удастся. Поэтому пусть тангенс половины угла равный t, тогда синус превратится по формуле
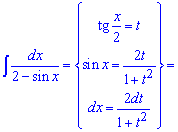
После раскрытия скобок в знаменателе получим квадратный трехчлен
Для сведения такой дроби к табличному арктангенсу в знаменателе сначала выделяем квадратный трехчлен
Не забываем в конце вернуться к выполненной в начале замены. Это важно при тестах и контрольных.
Пример 24. Здесь можем использовать универсальную тригонометрическую замену, а может пойти другим путем. Вынесем в знаменателе синус в квадрате за скобки и перегруппируем слагаемые в скобках, чтобы по тригонометрическим формулам получить котангенс. Его и обозначим за новую переменную u, вычисляем также дифференциал du и подставляем все в интеграл
В результате интегрирования получим табличную формулу арктангенса
Пример 25. Необходимо вычислить интеграл от тангенса в квадрате от тройного аргумента. Сначала расписываем тангенс как часть синуса к косинусу. Далее синус в квадрате расписываем через косинус. После деления числителя на знаменатель получим два интеграла которые без труда находим по формулам интегрирования
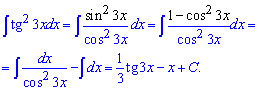
Как только Вы изучите приведенные схемы и методики сведения интегралов под то или иное правило, научитесь видеть в примерах табличные интегралы и преобразования, которые в несколько шагов позволят Вам найти интеграл — тогда контрольная работа, или «срезы» для Вас не будут препятствием в обучении. Для этого нужно решить с десяток различных интегралов к каждому из приведенных типов. Все остальные после этого будут для Вас подобными, а схема их вычислений очевидной и понятной. Если в обучении встречаются сложные интегралы или сомневаетесь в собственных силах помните — мы всегда готовы оказать помощь. Это предложение актуально не только для студентов стационарной формы обучения, но и для заочников и школьников. В 11 классе в обучении с недавних времен школьникам также приходится иметь дело с интегралами.
Готовые решения контрольной по интеграции
- < Предыдущие ответы
- Контрольная работа по интегрированию № 2
- Контрольная работа по интегрированию № 3
Интегрирование сложных тригонометрических функций
Прилагательное
«сложный» для большинства примеров
вновь носит во многом условный характер.
Начнем с тангенсов и котангенсов в
высоких степенях. С точки зрения
используемых методов решения тангенс
и котангенс – почти одно и тоже, поэтому
я больше буду говорить о тангенсе,
подразумевая, что продемонстрированный
прием решения интеграла справедлив и
для котангенса тоже.
На
уроке Интегралы
от тригонометрических функций мы
разобрали интеграл от тангенса в
квадрате. На уроке Как
вычислить площадь фигуры? в
примере 10 фигурировал тангенс в кубе.
В том примере для нахождения интеграла
от тангенса в кубе мы применяли
тригонометрическую формулу
.
Интеграл от тангенса в четвертой, пятой
степени (редко в более высоких степенях)
решается с помощью этой же формулы!
Пример
15
Найти
неопределенный интеграл
Идея
решения подобных интегралов состоит в
том, чтобы с помощью формулы
«развалить»
исходный интеграл на несколько более
простых интегралов:
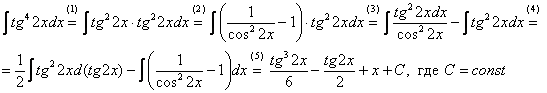
(1)
Готовим подынтегральную функцию к
применению формулы.
(2) Для одного из
множителей используем формулу
(3)
Раскрываем скобки и сразу же используем
свойство линейности неопределенного
интеграла.
(4) В первом интеграле
используем метод
подведения функции под знак дифференциала.
Во втором интеграле еще раз используем
формулу
,
в данном случае
.
(5)
Берём все три интеграла и получаем
ответ.
Пример
16
Найти
неопределенный интеграл
Это
пример для самостоятельного решения.
Для котангенса существует аналогичная
формула:
.
Полное решение и ответ в конце урока.
Если
возникли затруднения или недопонимание,
следует вернуться к уроку Интегралы
от тригонометрических функций.
На
вышеупомянутом уроке мы
рассматривали универсальную
тригонометрическую подстановку для
решения определенного вида интегралов
от тригонометрических функций. Недостаток
универсальной тригонометрической
подстановки заключается в том, что при
её применении часто возникают громоздкие
интегралы с трудными вычислениями. И в
ряде случаев универсальной тригонометрической
подстановки можно избежать!
Рассмотрим
еще один канонический пример, интеграл
от единицы, деленной на синус:
Пример
17
Найти
неопределенный интеграл
Здесь
можно использовать универсальную
тригонометрическую подстановку и
получить ответ, но существует более
рациональный путь. Я приведу полное
решение с комментами к каждому шагу:

(1)
Используем тригонометрическую формулу
синуса двойного угла
.
(2)
Проводим искусственное преобразование:
В знаменателе делим и умножаем на
.
(3)
По известной формуле в знаменателе
превращаем дробь в тангенс.
(4) Подводим
функцию под знак дифференциала.
(5)
Берём интеграл.
Пара
простых примеров для самостоятельного
решения:
Пример
18
Найти
неопределенный интеграл
Указание:
Самым первым действием следует
использовать формулу приведения
и
аккуратно провести аналогичные
предыдущему примеру действия.
Пример
19
Найти
неопределенный интеграл
Ну,
это совсем простой пример.
Полные
решения и ответы в конце урока.
Думаю,
теперь ни у кого не возникнет проблем
с интегралами:
и
т.п.
В
чём состоит идея метода? Идея состоит
в том, чтобы с помощью преобразований,
тригонометрических формул организовать
в подынтегральной функции только
тангенсы и производную тангенса
.
То есть, речь идет о замене:
.
В Примерах 17-19 мы фактически и применяли
данную замену, но интегралы были настолько
просты, что дело обошлось эквивалентным
действием – подведением функции под
знак дифференциала.
Примечание:
аналогичные рассуждения, как я уже
оговаривался, можно провести и для
котангенса.
Существует
и формальная предпосылка для применения
вышеуказанной замены:
Сумма
степеней косинуса и синуса – целое
отрицательное число.
Для
интеграла
–
целое отрицательное число.
Для
интеграла
–
целое отрицательное число.
Для
интеграла
–
целое отрицательное число.
Рассмотрим
пару более содержательных примеров на
это правило:
Пример
20
Найти
неопределенный интеграл
Сумма
степеней синуса и косинуса
:
2 – 6 = –4 – целое отрицательное число,
значит, интеграл можно свести к тангенсам
и его производной:

(1)
Преобразуем знаменатель.
(2) По
известной формуле получаем
.
(3)
Преобразуем знаменатель.
(4) Используем
формулу
.
(5)
Подводим функцию под знак дифференциала.
(6)
Проводим замену
.
Более опытные студенты замену могут и
не проводить, но все-таки лучше заменить
тангенс одной буквой – меньше риск
запутаться.
Далее
берётся простой интеграл и проводится
обратная замена.
Пример
21
Найти
неопределенный интеграл
Это
пример для самостоятельного решения.
Держитесь,
начинаются чемпионские раунды =)
Зачастую
в подынтегральной функции находится
«солянка»:
Пример
22
Найти
неопределенный интеграл
В
этом интеграле изначально присутствует
тангенс, что сразу наталкивает на уже
знакомую мысль:

Искусственное
преобразование в самом начале и остальные
шаги оставлю без комментариев, поскольку
обо всем уже говорилось выше.
Пара
творческих примеров для самостоятельного
решения:
Пример
23
Найти
неопределенный интеграл
Пример
24
Найти
неопределенный интеграл
Да,
в них, конечно, можно понизить степени
синуса, косинуса, использовать
универсальную тригонометрическую
подстановку, но решение будет гораздо
эффективнее и короче, если его провести
через тангенсы. Полное решение и ответы
в конце урока
У
многих читателей могло сложиться
впечатления, что я немного подустал.
Отнюдь. За окном февральский ветер –
самая атмосфера для лекций. Естественно,
данная страничка создана не за один
день, я успел несколько раз побриться,
регулярно кушаю и так далее. К тому же,
загружать студентов – удовольствие
бесконечное =). …Шутка! На самом деле
моя миссия – разгружать посетителей
сайта. Вагонами.
Переходим
к заключительному пункту познавательного
путешествия в мир сложных интегралов:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
You should upgrade or use an alternative browser.
-
Forums
-
Homework Help
-
Calculus and Beyond Homework Help
Integral of tangent squared of x
-
Thread starter
grief -
Start date
Dec 11, 2005 -
-
Tags -
Integral
Tangent
-
- Dec 11, 2005
- #1
Answers and Replies
- Dec 11, 2005
- #2
- Dec 11, 2005
- #3
1 + (tan(x))^2 = (sec(x))^2
and we know that the derivative of tan(x) is (sec(x))^2
then it’s easy to find the integral of (tan(x))^2
- Dec 11, 2005
- #4
P.S.: What «quotient» did you get that you were having trouble integrating? If I could see it, maybe I could give a hint on how to integrate it.
P.P.S.: people learn better when you give them hints, or direction on the problem than when you do most of the steps for them and just leave a short blank at the end. :grumpy:
- Dec 11, 2005
- #5
- Dec 11, 2005
- #6
never mind, I was on the wrong track.
I’m not so sure. You certainly weren’t on the easy track, but I am not yet ready to believe you were on the wrong track.
Suggested for: Integral of tangent squared of x
- Dec 29, 2022
- Oct 26, 2022
- Mar 23, 2023
- Jan 5, 2022
- Aug 15, 2022
- Mar 26, 2022
- Apr 4, 2023
- Feb 13, 2023
- Sep 15, 2022
- Dec 1, 2022
-
Forums
-
Homework Help
-
Calculus and Beyond Homework Help
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Subscribe to verify your answer
Subscribe
Sign in to save notes
Sign in
Number Line
Examples
-
int e^xcos(x)dx
-
int cos^3(x)sin (x)dx
-
int frac{2x+1}{(x+5)^3}
-
int_{0}^{pi}sin(x)dx
-
int_{a}^{b} x^2dx
-
int_{0}^{2pi}cos^2(theta)dtheta
-
partial:fractions:int_{0}^{1} frac{32}{x^{2}-64}dx
-
substitution:intfrac{e^{x}}{e^{x}+e^{-x}}dx,:u=e^{x}
- Show More
Description
Integrate functions step-by-step
integral-calculator
inttan^{2}(x)dx
en
Related Symbolab blog posts
High School Math Solutions – Partial Fractions Calculator
Partial fractions decomposition is the opposite of adding fractions, we are trying to break a rational expression…
Read More
Enter a problem
Save to Notebook!
Sign in
Алгебра Упрощение тригонометрических выражений
Материалы к уроку
Конспект урока
14. Упрощение тригонометрических выражений
Равенства
Часто они используются при упрощении и доказательстве тригонометрических выражений.
Рассмотрим примеры использования этих формул при упрощении тригонометрических выражений.
( вынесем за скобку общий множитель косинус квадрат тэ, в скобках получим разность единицы и квадрата косинуса тэ, что равно по первому тождеству квадрату синуса тэ. Получим сумму синус четвертой степени тэ произведения косинус квадрат тэ и синус квадрат тэ. общий множитель синус квадрат тэ вынесем за скобки, в скобках получим сумму квадратов косинуса и синуса, что по основному тригонометрическому тождеству равно единице. В итоге получим квадрат синуса тэ).
( Вынесем общий множитель косинус тэ за скобки, а в скобках приведем к общему знаменателю, который представляет собой произведение один минус синус тэ на один плюс синус тэ.
В числителе получим: единица плюс синус тэ плюс единица минус синус тэ, приводим подобные, числитель равен двум после приведения подобных.
В знаменателе можно применить формулу сокращенного умножения (разность квадратов) и получить разность единицы и квадрата синуса тэ, что по основному тригонометрическому тождеству
равно квадрату косинуса тэ. После сокращения на косинус тэ получим конечный ответ : два деленное на косинус тэ).
Рассмотрим примеры использования этих формул при доказательстве тригонометрических выражений.
ПРИМЕР 4.Найти значение выражения tg 2 t + ctg 2 t ,если tg t + ctg t = 6.
( сумма квадратов тангенса тэ и котангенса тэ, если сумма тангенса и котангенса равна шести).
Решение. (tg t + ctg t)2 = 62
tg 2 t + 2 ∙ tg t ∙ctg t + ctg 2 t = 36
tg 2 t + 2 + ctg 2 t = 36
tg 2 t + ctg 2 t = 36-2
tg 2 t + ctg 2 t = 34
Возведем обе части исходного равенства в квадрат:
(tg t + ctg t)2 = 62 ( квадрат суммы тангенса тэ и котангенса тэ равна шести в квадрате).
Так как произведение тангенса тэ на котангенс тэ равно единице, то tg 2 t + 2 + ctg 2 t = 36 ( сумма квадратов тангенса тэ и котангенса тэ и двух равна тридцати шести),
значит tg 2 t + ctg 2 t = 34 (сумма квадратов тангенса тэ и котангенса тэ равна тридцати четырем). Ответ: 34.
Остались вопросы по теме? Наши репетиторы готовы помочь!
-
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
-
Найдём слабые места по предмету и разберём ошибки
-
Повысим успеваемость по школьным предметам
-
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Mathway | Популярные задачи
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) ) |
|
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) |
|
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) ) |
|
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) |
|
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
2{theta}-1$
Квадрат функции загара, равный вычитанию единицы из квадрата функции секущей, называется формулой квадрата загара. Его также называют квадратом идентичности функции загара.
Введение
Касательные функции часто используются в тригонометрических выражениях и уравнениях квадратной формы.
Таким образом, получается, что квадрат функции тангенса равен вычитанию из квадрата функции секущей.
Последние математические темы
ноября 03, 2022
соседних сторон четырехсторонних
сентябрь 06, 2022
Доказательство для взаимного правила фракций или рациональных номеров
июля 242, 2022
Стандарт Antry aftion
9001 Стандарт
. 15 июля 2022 г.
Геометрическое доказательство стандартного уравнения окружности 9circ}}$
Функция тангенса-квадрата — Исчисление
Эта статья о конкретной функции из подмножества действительных чисел в действительные числа. В статье представлена информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференцированию и интегрированию.
Посмотреть полный список конкретных функций на этой вики
Для функций, включающих углы (тригонометрические функции, обратные тригонометрические функции и т.
д.), мы следуем соглашению, что все углы измеряются в радианах. Так, например, угол измеряется как .
Содержание
- 1 Определение
- 2 Ключевые данные
- 3 Дифференциация
- 3.1 Первая производная
- 4 Интеграция
- 4.1 Первая первообразная
- 4.2 Вторая первообразная
- 4.3 Высшие первообразные
- 4.4 Интегрирование произведений с полиномами
Определение
Эта функция определяется как композиция функции квадрата и функции тангенса. В явном виде это функция:
записывается как стенография.
Ключевые данные
| Товар | Значение |
|---|---|
| Домен по умолчанию | все действительные числа кроме нечетные целые числа кратные . |
| диапазон | , т. е. . Все неотрицательные действительные числа. нет абсолютного максимального значения; абсолютное минимальное значение 0 |
| период | , т. е. . е. .
|
| локальные максимальные значения и точки достижения | Нет локальных максимальных значений |
| местные минимальные значения и точки достижения | 0 во всех целых кратных . |
| точки перегиба (обе координаты) | Нет |
| вертикальные асимптоты | во всех нечетных кратных , с функцией, идущей в обоих направлениях в каждом случае. |
| производная | |
| первообразная | . Обратите внимание, что значение должно быть постоянным в пределах каждого интервала между последовательными нечетными числами, кратными , но может отличаться в разных интервалах. Домен вообще не подключен. |
| Описание интервала на основе увеличения/уменьшения и вогнутости вверх/вниз | Для каждого целого числа: по убыванию и вогнутости от до по возрастанию и вогнутости от до . |
Дифференцирование
Первая производная
Первую производную можно вычислить, комбинируя цепное правило дифференцирования и знание производных функции квадрата и функции тангенса:
Интегрирование
Первая первообразная
Используем тождество:
Используя это, мы перепишем:
где мы используем, что функция тангенса является первообразной для функции квадрата секанса
Вторая первообразная
Мы можем антидифференцировать функцию еще раз:
Старшие первообразные
Невозможно вычислить высшие первообразные в терминах элементарных функций, но мы можем вычислить их с помощью полилогарифма.

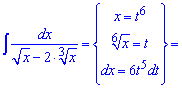
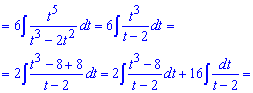
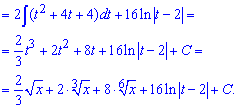
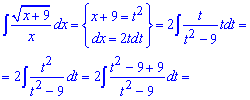
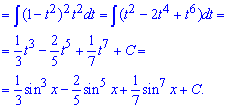
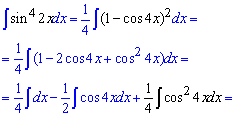
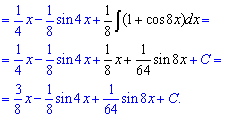
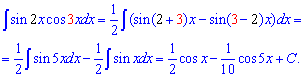
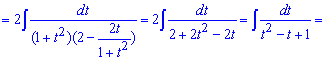
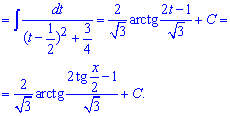
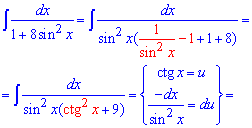

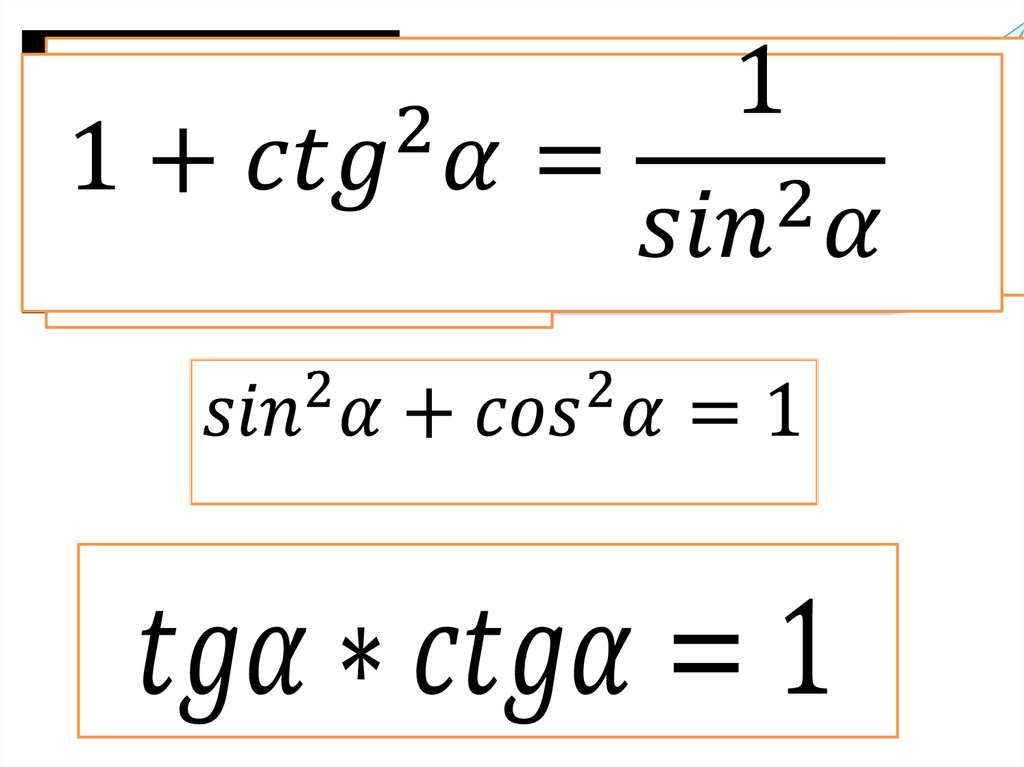 д.), мы следуем соглашению, что все углы измеряются в радианах. Так, например, угол измеряется как .
д.), мы следуем соглашению, что все углы измеряются в радианах. Так, например, угол измеряется как . 