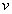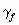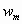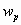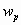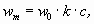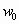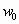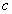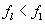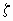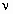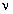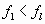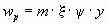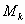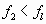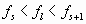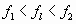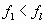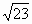Как найти первую частоту собственных колебаний - Исправление недочетов и поиск решений вместе с Examum.ru

Верификационные примеры

Аналитическое

решение

этой

задачи

имеет

вид

[2]:

кр

= K

π2 D

b2h

где

E – модуль упругости,

D =

Eh3

– цилиндрическая жесткость пластины,

12(1−ν 2 )

K —

коэффициент, значение которого зависит от способа закрепления краёв пластинки и

отношения

(в данном случае K =1.33 ).

π2 D

Таким образом, σкр

= K

= 0.8401×10

Выполнив расчет при помощи T-FLEX Анализ, получили следующие результаты:

−q

Тип конечного

Параметры сетки

Результат, критическая

Ошибка

δ =

кр

×100%

элемента

нагрузка

σкр

Линейный

0.8370 ×10

0.37 %

треугольник

Число узлов: 2105

м2

Число КЭ: 4040

Квадратичный

0.8391×10

0.12 %

треугольник

м2

Квадратичный

Число узлов: 4450

0.8388×10

0.15 %

тетраэдр (10 узлов)

Число КЭ: 12833

м2

Примеры задач частотного анализа

Определение собственных частот колебаний балки

Имеется консольно-защемленная балка длиной			h


L с прямоугольным поперечным сечением



шириной b и высотой h.	L	b

Требуется определить первые три собственные частоты балки.

Примем L=0.5 м, b=0.05 м, h=0.02 м.

Свойства материала: модуль упругости E = 2.1 1011 Па, коэффициент Пуассона ν = 0.28 , плотность

ρ = 7800 кг м3 .

Построив модель, создаем задачу типа «Частотный анализ».

Конечно-элементная модель балки с закреплениями

141

Руководство пользователя T-FLEX Анализ

Аналитическое решение имеет вид [3, с.382]:

		E J	1 k	i	2
fi	=					,
		l
		ρ F 2π

где fi — собственные частоты, E – модуль упругости материала, J – момент инерции, ρ – плотность материала, F – площадь поперечного сечения, l – длина балки, ki — коэффициент, зависящий от формы колебаний ( k1 =1.875, k2 = 4.694, k3 = 7.855 ).

Результаты получились следующие:

	Форма колебаний	Решение в T-FLEX,	Аналитическое		Погрешность, %
		Гц	решение, Гц
		67.3	67.0		0.4

		419.1	420.2		0.3

		1161.4	1176.7		1.3

Определение первой собственной частоты колебаний круглой пластинки
	Для круглой пластины радиуса R и толщины h, защемленной по
	контуру, необходимо определить собственную частоту первой
	формы колебаний.			R		h

	Примем радиус пластины равным R=0.2 м, толщину пластины
	h=0.01 м. Свойства материала: модуль упругости E = 2.1 1011 Па,
	коэффициент Пуассона ν = 0.225 , плотность ρ = 7800 кг	3 .
		м

Вследствие симметрии рассматриваем одну четвертую часть пластины, накладываем соответствующие граничные условия.

Выполним расчёт первой собственной частоты колебаний пластины, используя сначала тетраэдральные конечные элементы, а затем – треугольные. Сравним полученные результаты с аналитическим решением, которое имеет вид [3, с.452]:

f =	10.21		D	= 624.5 Гц,
R2 2π		ρ h

где R – радиус пластины, ρ – плотность материала, h – толщина пластины, D =			E h3	– изгибная
12	(1−ν2 )

жесткость.

142

Верификационные примеры

Конечно-элементная модель пластины с закреплениями

Выполнив расчет при помощи T-FLEX Анализ, получили следующие результаты:

Тип конечного	Параметры сетки	Результат, первая	Ошибка δ =		f −	λ1	×100%

элемента		собственная частота λ1
		f


Квадратичный	Число узлов: 3938	622.1	Гц	0.39 %
тетраэдр	Число КЭ: 11549


Линейный	Число узлов: 1865	623.0 Гц	0.24 %
треугольник

	Число КЭ: 3580
Квадратичный	621.5	Гц	0.48 %
треугольник

Первая форма колебаний

Свободные колебания сферического купола

Рассмотрим сферический купол радиуса R , защемлённый по контуру (см. рис.).

Толщина купола h существенно меньше его радиуса R .

143

Руководство пользователя T-FLEX Анализ

Численно моделировалась 14 часть сферической поверхности. На нижней кромке задавались условия жёсткого защемления, на боковых гранях – условия симметрии.

Конечно-элементная модель сферической оболочки с закреплениями

Примем следующие исходные данные: радиус

R = 300мм, толщина h = 3мм (

=100 ).

Па, ν = 0.28,

кг

Характеристики материала: E = 2 ×10

ρ = 7800

м3

Решение этой задачи имеет вид [4]: fi

ki ω0

, ω

2π

ρR2 (1−ν 2 )

E – модуль упругости,

где

ki — коэффициент, значение которого для первых пяти частот: 0.5457 ,

0.7377 , 0.8563 ,

0.8598 , 0.9034 .

Таким образом, f1 =1564.7 Гц, f2 = 2115.3 Гц, f3 = 2455.4 Гц, f4 = 2465.4 Гц , f5 = 2590.4 Гц.

Выполнив расчет при помощи T-FLEX Анализ, получили следующие результаты:

Тип конечного	Параметры сетки	Результат, собственные	Ошибка δ =		fi −λi	×100%

частоты λi
элемента				fi

		1574.1 Гц	0.59 %
Линейный	Число узлов: 2840	2107.0 Гц	0.39 %
2469.9	Гц	0.59 %
треугольник	Число КЭ: 5510
2490.3	Гц	1.01 %

		2592.9 Гц	0.10 %

144

					Верификационные примеры

		1573.8 Гц	0.58 %
Квадратичный		2105.4 Гц	0.47 %
	2466.7	Гц	0.46 %
треугольник
	2488.5	Гц	0.94 %

		2586.7 Гц	0.14 %
				0.61 %
		1574.3 Гц
Квадратичный	Число узлов: 5507	2106.2 Гц	0.43 %
2465.9	Гц	0.43 %
тетраэдр (10 узлов)	Число КЭ: 16387
2487.0	Гц	0.88 %

		2586.1 Гц	0.17 %

145

Соседние файлы в папке Лекции Т

Источник

среда: Сб.науч.тр. / Респ. науч.-практ. центр гигиены: Гл. ред. Л.В.Половинкин. — Минск: ГУ РНМБ, 2011. — Вып. 18. — с. 63-68.

5. Чеботарев, П.А. Факторы производственной среды и трудовой деятельности работников производства

топлив и растворителей на нефтеперерабатывающем предприятии / П.А.Чеботарев, Н.В.Харлашова // Гигиена и санитария Науч.-практ. журнал. / Изд-во «Медицина», Москва. — Выпуск № 5, 2012г. -с.79-82.

ОПРЕДЕЛЕНИЕ ЧАСТОТ СОБСТВЕННЫХ КОЛЕБАНИИ МНОГОЭТАЖНЫХ ЗДАНИИ

Хазов Павел Алексеевич

Ст. преп. кафедры теории сооружений и технической механики, ННГАСУ, Нижний Новгород

Кофорова Оксана Михайловна

студент, ННГАСУ, Нижний Новгород

Согласно СП 20.13330.2011 «Нагрузки и воздействия» (актуализированная редакция СНиП 2.01.07-85*), для определения ветровой нагрузки на здания или сооружения необходимо использовать формулу (11.1) [2, с. 17]:

щ = Щ + Щ

т р

(1)

где

т — средняя составляющая ветровой нагрузки, р

пульсационная составляющая ветровой нагрузки.

Значение средней составляющей ветровой нагрузки не зависит от каких-либо упругих или динамических свойств изучаемого сооружения. Для ее определения в какой-либо точке достаточно знать форму сооружения, тип местности, в которой оно расположено, а также высоту точки над уровнем поверхности земли.

Значение пульсационной составляющей ветровой нагрузки определяется согласно п. 11.1.8 [2, с.20]. При этом для выбора метода расчета необходимо знать значения частот собственных колебаний.

Чаще всего достаточно определить значение первой и второй собственных частот.

В общем случае любое здание представляет собой систему с бесконечным числом динамических степеней свободы, поскольку все элементы здания имеют массу и являются упругими.

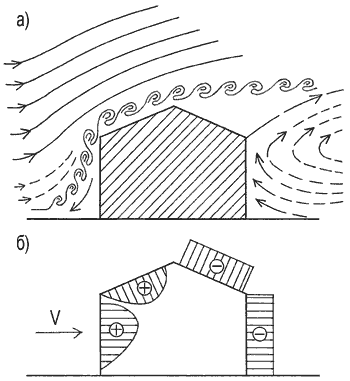
Для каркасных многоэтажных зданий с большой степенью точности можно предположить, что все входящие в систему массы сосредоточены в уровнях перекрытий. Это означает, что здание можно рассмотреть, как консольный стержень с количеством сосредоточенных на нем масс, равным количеству этажей здания и жесткостью, эквивалентной жесткости всего здания (рис 1а) [3, с. 147].

В общем случае такая система имеет п собственных частот. Примеры возможных форм колебаний показаны на рис. 1 (б, в, г). При этом наиболее вероятная форма колебания, соответствующая первой (наименьшей) собственной частоте, показана на рис. 1а.

Рис.1. Динамическая расчетная схема многоэтажного здания (а) и некоторые формы колебаний (б-г)

Для определения собственных частот такой си- 8

стемы необходимо раскрыть определитель матрицы пере- где ^ — удельное перемещение точки сосредоточения ь

мещений-частот W [3, с. 151]: 1

ш =

8цМ 1 — 2

822М 21

8„М „ —

той массы от единичной силы, приложенной в точке со-

средоточения _]-той массы. лебаний системы.

Тогда уравнение частот примет вид:

— частота собственных ко-

(2)

АегШ =

8иМ,—г

82М 2

8„М,—2

п2

п3

Решениями уравнения (3) являются корни многочлена п-ной степени:

апЛ» + а. Л»1 + а, Л»2 +

п -2

где

Л = — а>

. + а»-1Л + а» = 0, (4)

Для зданий с большим количеством этажей вычисления становятся очень громоздкими, поскольку возникает необходимость раскрытия определителя матрицы п-ного порядка, после чего необходимо определить корни многочлена п-ной степени. При этом, зачастую, практический смысл имеет только первая частота собственных колебаний, поскольку именно форма, соответствующая первой частоте, является наиболее вероятной формой колебания здания.

Для определения первой собственной частоты предлагается использовать простой перебор случайных

значений ^ . Тогда выражение (3) будет представлять собой определитель числовой матрицы, который удобно вычислять с помощью встроенного математического оператора программного комплекса МЕ БХБЬ, позволяющего восстановить определитель числовой матрицы любого порядка.

Важной задачей также является определение эквивалентной жесткости стержня. Для этого предлагается использовать условие равенства горизонтальных перемещений точек А1 и А2 (рис.2,а,б) при действии эквивалентных нагрузок.

Величину перемещения 1 следует определять из статического расчета конечно-элементной модели зда-

А А Р

ния. Перемещение 2 определяется по формуле Мора-Максвелла (рис. 2,в) [1, с. 168]:

Рис.2. К определению эквивалентной жесткости стержня

р ■ н

А =р зд

АР 3Е/

(8)

откуда:

Р ■ н ы = р н

А А 2Р =

‘ МрИл1 ЕТ„„

3 А,

0 «экв . (5)

Раскроем интеграл (5) с помощью правила Вере-

щагина [1, с. 173]: 1

А АР =

А 2Р ЕI

1 зд

1 2 Р ■ Н3

■ 2 ■ Р ■ Нзд ‘ Нзд ‘ 3 ■ Нзд = «

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

экв 2 3 3Е1 экв (6)

вид:

Условие эквивалентности жесткостей примет

А АР = А АР А 2Р А1Р (7)

или, с учетом (6):

(9)

При этом можно задаваться любой величиной силы

А АР

P, учитывая, что величина перемещения 1 всегда пропорциональна ей. Для повышения точности расчета рекомендуется выбирать силу P таким образом, чтобы переме-

ААР _

щение 1 не было исчезающее мало.

Рассмотрим решение задачи по определению первой собственной частоты на примере шестнадцатиэтажного каркасного здания, изображенного на рис.3. Элементы матрицы перемещений-частот W определяется с помощью ПВК «Полюс» с учетом правила взаимности

— = 8Ц ( ,ч

удельных перемещений: 7 7 (рис.3).

1 N-

.0х=49066 9 DX=44472 ,DX=39914 ,DX=35427.9 ,DX=31049.6 ,DX=26815 ,DX=22760.1 #DX=18920.8 ,DX=15333.1 ^DX=12128.3 #DX=9056.12 (DX=6438.71 ,DX=4216.61 DX=2425.75 ¡DX=1102.07 i DX=281.506

m DX=44472 .DX=40429.1 ,DX=36392.2 #DX=32391.2 ,DX=28462.1 >DX=24640.8 ,DX=20963.2 #DX=17465.4 #DX=14183.1 #DX=11240.2 .DX=8409.26 (DX=5989.5 .

^х^зэгз.п DX=2264.03 DX=1030.19 DX=263.538

ф DX=3S914 >DX=36392.2 #DX=32870.4 #DX=29354.5 #DX=25874.6 #DX=22466.6 #DX=19166.4 ,DX=16009 9 ,DX=13033.2 ,DX=10352.1 eDX=7762.39 >DX=5540.29 (DX=3641.62 DX=2102.31 _DX=958.32 i DX=245.569

ф0х=281.506

#DX=263.538

.DX=245.569

,DX=227.601

,DX=209.632

>DX=191.GG4

.DX-173.895

#DX=155.727

#DX=137.758

,DX=120.334

#DX=101.321

#DX=83.853

#DX=65.8845

,DX=47.916

(DX=29.9475

DX=11.979

Рис.3. К определению элементов матрицы перемещений-частот

Для определения эквивалентной жесткости стер- SCAD. Результаты статического расчета от воздействия жня была построена конечно-элементная модель в ПВК единичной горизонтальной силы приведены на рис.4.

t&mjL:

sft ■ |

£ Hi’

.SSL

■ 14

■ 13

■ 12

□ 11

□ 10

□ 9

□ 8

□ 7

□ 6

□ 5

□ 4

□ 3

□ 2

ШЩ о

Рис.4. Горизонтальные перемещения точек здания

С учетом полученного перемещения верхней точки здания, используя формулу (9), получаем:

P ■ H

3Г

= 3,50 ■ 108 кНм2

Значения сосредоточенных в перекрытии масс представляет собой сумму расчетных значений всех постоянных нагрузок на перекрытие: собственного веса перекрытия, вышележащих ограждающих конструкций, перегородок, конструкций полов, колонн, определяемых согласно [1].

Транспонированная матрица масс в запишется в следующем виде (размерность — тонны):

Мт=(М1, М2…..М16)=

=(96; 252; 254; 253; 253; 252; 249; 252; 253; 253; 25

2; 254; 255; 251; 254; 254) Элементы главной диагонали матрицы W вычисляются в зависимости от текущего значения частоты ю.

Определитель матрицы W восстанавливается автоматически.

Приведем пример матрицы перемещений-частот при значении частоты ю = 7.24 рад -1:

-198 4.45 3.99 3.54 3.11 2.68 2.28 1.89 1.53 1.20 0.91 0.64 0.42 0.24 0.11 0.03

4.45 358 3.64 3.24 2.85 2.46 2.10 1.75 1.42 1.12 0.84 0.59 0.39 0.23 0.10 0.02

3.99 3.64 166 2.94 2.59 2.25 1.92 1.60 1.30 1.03 0.78 0.55 0.36 0.21 0.10 0.02

3.54 3.24 2.94 -0.06 2.33 2.03 1.74 1.46 1.19 0.94 0.71 0.51 0.34 0.19 0.09 0.02

3.11 2.85 2.59 2.33 -143 1.81 1.56 1.31 1.07 0.85 0.65 0.46 0.31 0.18 0.08 0.02

2.68 2.46 2.25 2.03 1.81 -264 1.38 1.16 0.96 0.76 0.58 0.42 0.28 0.16 0.07 0.02

2.28 2.10 1.92 1.74 1.56 1.38 -364 1.02 0.84 0.68 0.52 0.37 0.25 0.15 0.07 0.02

W II 0 1.89 1.75 1.60 1.46 1.31 1.16 1.02 -447 0.73 0.51 0.45 0.33 0.22 0.13 0.06 0.02

1.53 1.42 1.30 1.19 1.07 0.96 0.84 0.73 -513 0.50 0.39 0.29 0.19 0.11 0.05 0.01

1.20 1.12 1.03 0.94 0.85 0.76 0.68 0.51 0.50 -563 0.33 0.24 0.16 0.10 0.04 0.01

0.91 0.84 0.78 0.71 0.65 0.58 0.52 0.45 0.39 0.33 -603 0.20 0.13 0.08 0.04 0.01

0.64 0.60 0.55 0.51 0.46 0.42 0.37 0.33 0.29 0.24 0.20 -631 0.11 0.06 0.03 0.01

0.42 0.39 0.36 0.34 0.31 0.28 0.25 0.22 0.19 0.16 0.13 0.11 -649 0.05 0.02 0.01

0.24 0.23 0.21 0.19 0.18 0.16 0.15 0. 13 0.11 0.10 0.08 0.06 0.05 -660 0.02 0.005

0.11 0.10 0.10 0.09 0.08 0.07 0.07 0.06 0.05 0.04 0.04 0.03 0.02 0.02 -666 0.003

0.03 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.01 0.01 0.01 0.01 0.01 0.005 0.003 -668

Получить точное решение уравнения (3) простым рицы. Тем не менее, удалось получить значения ю, при пе-подбором не удалось. При очень малом изменении ча- реходе между которыми меняется знак определителя. Гра-стоты сильно изменяется значение определителя мат- фик зависимости с1с1|У| = Г(т) представлен на рис.5.

Графически определяем значение первой собственной частоты: ю=7,24046 рад -1.

Обычно при решении подобных задач ограничиваются точностью определения изучаемых величин до тре-тьего-четвертого значимого знака. Таким образом, в расчетах можно принимать ю=7,24 рад -1.

В случае необходимости, последующие частоты определяются подобным образом.

Для определения собственных частот механических систем так же можно использовать модальный анализ конечно-элементной схемы, смоделированной в каком-либо программно-вычислительном комплексе. При этом необходимо учесть все динамические особенности модели. Этот метод дает наиболее точные результаты.

Представленный в настоящем сообщении метод отличается, в первую очередь, своей простотой, и может быть рекомендован при выполнении инженерных расчетов зданий и сооружений.

Список литературы

1. А.В. Дарков, Н.Н. Шапошников. Строительная механика. — М.: Высшая школа, 1986. — 608 с.

2. Н.А. Попов, И.В. Лебедева, И.И. Ведяков. СП 20.13330.2011 «Нагрузки и воздействия». Актуализированная редакция СНиП 2.01.07-85*: свод правил. М.: Минрегион России, 2010. — 81 с.

3. Р. Клаф, Дж. Пензиен. Динамика сооружений. -New York, 1975. — перевод: М.: Стройиздат. — 1979. — 320 с.

ПОДХОД К РАЗРАБОТКЕ МЕТОДОВ И МОДЕЛЕЙ ПРОТИВОДЕЙСТВИЯ

КОМПЬЮТЕРНЫМ АТАКАМ

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Варлатая Светлана Климентьевна

кандидат технических наук, профессор кафедры информационной безопасности ДВФУ, г. Владивосток

Кирьяненко Александр Васильевич Курашинов Тимур Мугамедович

аспирант кафедры информационной безопасности ДВФУ, г. Владивосток

АННОТАЦИЯ

Целью данной статьи является рассмотрение вопросов обеспечение устойчивости функционирования критически важной информационной системы (КВИС) в динамике ее применения и в условиях массированного воздействия

Источник

Известно, что основной нагрузкой для высотных сооружений является ветровая. Однако в современных пакетах автоматизированного расчета крайне скудно освещена теоретическая база расчета сооружений на ветровую нагрузку, что затрудняет их использование проектировщиками. Авторы настоящей статьи, в которой кратко излагаются некоторые теоретические основы расчета сооружений на ветровую нагрузку по нормам /1/ и приведены два примера, выражают надежду, что она в некоторой степени поможет инженерам-проектировщикам более эффективно использовать пакет “ЛИРА” и другие программные средства.

Ветровое нормальное давление на препятствие определяется по формуле /2/:

(1)

где

— скорость ветра, м/с;

— плотность воздуха, кг/м³, зависящая от его влажности, температуры и атмосферного давления.

Скорость и направление ветра в данной точке считаются непостоянными, зависящими от времени. На рис. 1 по данным /2/ изображен график зависимости скорости ветра от времени, из которого видно, что скорость ветра осциллирует или пульсирует около среднего значения

. В обиходе это явление называют порывистостью. Заметим, что колебания скорости ветра около среднего значения не вызывают изменения знаков усилий и напряжений в большинстве элементов сооружений /3/. Поэтому в наших нормах /1/ представляют ветровую нагрузку

на сооружение в виде статической составляющей

, соответствующей средней скорости ветра

(рис. 1) и динамической добавки

(пульсационной составляющей, которая соответствует разности между средней и истинной скоростями ветра). То есть:

(2)

где

— коэффициент надежности по ветровой нагрузке, равный 1,4 /1/;

— нормативное значение средней составляющей ветровой нагрузки на высоте z над поверхностью земли;

— нормативное значение пульсационной составляющей ветровой нагрузки на высотеz(динамическая добавка, вызванная пульсацией воздуха).

Величина

по /1/ определяется по формуле:

(3)

где

— нормативное значение ветрового давления. Принимается в зависимости от ветрового района, где строится сооружение. В Беларуси по данным /1/ имеются всего два ветровых района: Iа и I с соответствующими нормативными значениями

= 17 кгс/м²и

= 23 кгс/м²;

— коэффициент, учитывающий изменение ветрового давления по высоте. Принимается по /1/ также с учетом типа местности, где возводится сооружение.

— аэродинамический коэффициент.

На физическом смысле коэффициентасследует остановиться подробнее. Каждое здание с точки зрения аэродинамики является плохообтекаемым препятствием /4/. На рис. 2а по данным /2/ изображена картина обтекания здания потоком воздуха, где ясно видны зоны вихреобразования, зона турбулентности, а на рис. 2б — распределение ветрового давления по наружным поверхностям этого здания. Отметим, что в зависимости от скорости ветра, плотности воздуха, формы здания и шероховатости его наружных стен, наличия соседних сооружений, холмов и т.д. картина распределения давления может быть иной. При определении проекций ветровой нагрузки на различные направления в приложении 4 /1/ приводятся величиныc_x,c_y,c_e,c_fи аэродинамического коэффициента внутреннего давленияc_i.

Т.к. вероятностные характеристики ветрового давления с течением времени не меняются, то пульсация скорости ветра в точке турбулентного потока рассматривается как стационарный случайный процесс. Устанавливая корреляционные функции турбулентного ветрового потока на основании обработки экспериментальных данных, находят спектральную плотность и среднее квадратичное значение реакции для сооружения. Это позволяет определить средние квадратичные значения динамических перемещений сооружения и коэффициент динамичности. Потом строится график нормативного динамического коэффициента с учетом материала, из которого выполнено сооружение.

Нормативное значение пульсационной составляющей ветровой нагрузкиw_pопределяется поw_mв зависимости от динамических характеристик (собственных частот, степеней свободы и коэффициента внутреннего трения) сооружения, на которое действует ветровая нагрузка. Ветровое давление является существенно динамической нагрузкой, так как при ее действии в общем случае может меняться величина нагрузки, место ее приложения и направление. Вследствие упругих свойств сооружения при действии порывов ветра оно колеблется. При колебаниях в элементах сооружения возникают силы инерции, которые влияют на напряженно-деформированное состояние сооружения. В зависимости от соотношения между частотами собственных колебаний сооружения и частотой пульсации ветра, частотой срыва вихрей воздуха с сооружения в нем могут возникнуть случаи, близкие к резонансу. Это приведет к значительному увеличению усилий, напряжений и перемещений в элементах сооружения. Поэтому в нормах /1/ приводятся предельные значенияf_lчастот собственных колебаний сооружения в зависимости от ветрового района и материала сооружения, при которых допускается не учитывать пульсационную составляющую ветровой нагрузки. Если жеf_lнаходится в нижней части спектра собственных частот сооружения, то нормы рекомендуют рассматривать три случая.

Случай А:

Тогда

, (4)

где

— коэффициент пульсаций давления ветра, зависящий от высоты

над поверхностью земли и типа местности;

— коэффициент пространственной корреляции пульсаций давления ветра. Так как ветровая нагрузка определяется с какой-то долей вероятности (носит случайный характер), то величина

определяется на основании методов математической статистики.

Случай Б:

Относится к системам с одной степенью свободы (водонапорные башни, ветроэнергетические установки, ретрансляторы и другие мачтовые сооружения).

(5)

где: x

— коэффициент динамичности. Определяется по чертежу 2 /1/ в зависимости от параметра

и логарифмического декремента затухания материала сооружения d .

Случай В:если

и для симметричных в плане зданий, для которых

, (6)

где:

— масса сооружения на уровнеz, отнесенная к площади поверхности, к которой приложена ветровая нагрузка;

y— условное горизонтальное перемещение на уровнеzпо первой форме собственных колебаний;

y — коэффициент, определяемый посредством разделения сооружения наrучастков, в пределах которых ветровая нагрузка принимается постоянной, по формуле

(7)

гдеM_k— массаk-го участка сооружения;

y_k— условное горизонтальное перемещение по первой форме собственных колебаний на уровне расположения массы

;

w_pk— равнодействующая пульсационной составляющей ветровой нагрузки наk-ом участке сооружения. Определяется по формуле (4).

Случай Г:

Необходимо производить расчет с учетом первыхsформ собственных колебаний, где число

определяется из условия:

. (8)

Из вышеизложенного ясно, как сложен расчет на действие ветровой нагрузки. Он состоит из двух этапов. На первом инженер определяет частоты и формы собственных колебаний сооружения, на втором — производит расчет в зависимости от положенияf_lв спектре собственных колебаний сооружения.

Все эти случаи расчета запрограммированы в пакете “ЛИРА-Windows”. В пакете пульсационная составляющая ветровой нагрузки раскладывается в ряд по собственным формам колебаний конструкции, и расчет ведется для каждого члена ряда отдельно. При этом считается, что сооружение реагирует каждой формой своих собственных колебаний на ветровую нагрузку. Определяются дляi-го слагаемого разложения в ряд ветровой нагрузки силы инерцииZ_iкаждой колеблющейся массы. По ним определяются усилияM_i,Q_i,N_iи перемещения. Суммарное усилие на стадии вычисления расчетных сочетаний определяется по формуле:

(9)

гдеN_k— усилие в сечении от статической составляющей ветровой нагрузки;N_i— то же отi-го слагаемого пульсационной составляющей ветровой нагрузки.

Примеры расчета

Пример 1.Расчет дымовой трубы на пульсацию (пример передан инженером С.А. Черновой, институт “Белпромпроект”, Минск).

— труба по ГОСТ 1074-76 сd_н= 630 мм иd_в= 610 мм;

— ветровой район — I, тип местности — B;

— предельное значение частоты собственных колебанийf_l= 2,9 Гц (табл. 8, /1/).

Перед расчетом трубы на ветровую пульсацию находим частоты собственных колебаний трубыf₁иf₂с двумя массами и формы собственных колебаний. Воспользовавшись программным пакетом “ЛИРА”, на основании модального анализа получим:

а) частоты собственных колебаний:f₁= 1,6672 Гц ;f₂= 13,8748 Гц;

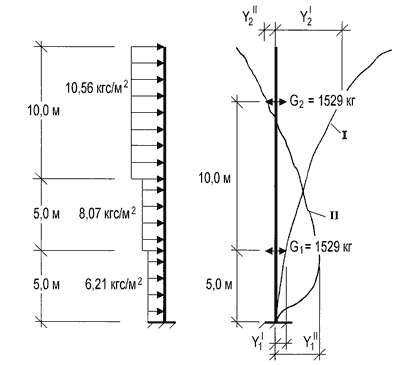
б) горизонтальные перемещения масс в соответствии с формами собственных колебаний (рис. 3):

— форма I —Y₁^I= 100 мм;Y₂^I= 667 мм;

— форма II —Y₁^II= 674 мм;Y₂^II= –101 мм.

Аэродинамический коэффициентсопределяем по Приложению 4 — /1/, номер схемы 14:

с = к× с_xh= 0,91× 0,59 = 0,54,

гдекопределяется по таблице 1 схемы 13 в зависимости от параметра l_e= 2× 20/0,63 = 63,4921;

с_xhопределяется по графику схемы 14 в зависимости от числа Рейнольдса (R_e= 9,17 × 10⁵,схема 12а) ветрового потока и отношения Δ/d= 0,0016.

Нормативное значение средней составляющей ветровой нагрузки на высотах 5, 10 и 15 м по формуле 6 /1/ будет соответственно 6,21, 8,07 и 10,56 кгс/м². Т.к. в нашем случае

, то для определения нормативных значений пульсационных составляющих ветровой нагрузкиw_pна высотеzбудем использовать формулу 10 /1/:

w_p=m×x× y× g.

m₁=m₂= 1539/(10× 0,63) = 242,698 кг/м²;

;

по чертежу 2 /1/ коэффициент динамичности x = 1,51.

Т.к. участков с различной величинойw_pтри, а масс — две, то для первой массы принимаем среднее значениеw_p(приz= 5 м иz= 10 м). Итак, по таблицам 7, 9 и 10 /1/ для первой массы z = 1,14, n = 0,88, для второй массы — z= 0,92, n = 0,88.

Равнодействующая пульсационной составляющей ветровой нагрузки для участков с массамиm₁иm₂:

w_p₁=(62,1 + 88,7)/2× 10× 0,63× 1,14× 0,88 = 451,259 Н;

w_p₂=105,6× 10× 0,63× 0,92× 0,88 = 538,611 Н.

По формуле 11 /1/ коэффициент y при горизонтальных перемещениях на уровнеzпо первой форме собственных колебанийy₁^I= 100 иy₂^I= 667:

y = (100× 451,259 + 667× 538,611) / (100^2×1529 + 667^2×1529) = 0,0005814.

Поэтому на высоте расположения первой массыz= 5 м:

w_p= 242,698× 1,51× 0,0005814× 100 = 21,307 Па.

То же на высоте расположения второй массыz= 15 м:

w_p= 242,698× 1,51× 0,0005814× 667 = 142,116 Па.

Согласно п. 6.8 /1/ для сооружений цилиндрической формы при

необходимо производить расчет на ветровой резонанс. Это объясняется колебаниями трубы в плоскости, перпендикулярной направлению ветрового потока из-за образования вихревой дорожки с шахматным расположением вихрей за трубой. Поэтому по формуле 29 /5/ находим критические значения скоростей для найденных форм собственных колебаний:

v_кр1=d/ (T_1×S_h) = 0,63 / (0,5998× 0,2) = 5,25 м/сек >v_{кр, min}= 0,64

= 0,64

= 3,07 м/с;v_кр₂=d/(T_2×S_h) = 0,63 / (0,072× 0,2) = 43,75 м/сек <v_{кр, max}= 25м/с,

где:T₁иT₂— периоды собственных колебаний;

S_h= 0,2 — число Струхаля для поперечного сечения в виде круга.

Как отмечается в /2/, для сооружений консольного типа допускается учитывать только первую форму собственных колебаний. Амплитуда динамической силы на уровне расположения первой массы при колебаниях по первой форме по формуле 30 /5/:

F₁(5) =F_{01× a 1}(5) = 2,661× 100/667 = 0,4 Н/м,

где: a₁(5) — относительная ордината первой формы собственных колебаний на высотеz= 5 м;

F₀₁=c_y×q_кр,_1×d= 0,25× 0,613× 5,25^2×0,63 = 2,661 Н/м — амплитуда интенсивности динамической силы на уровне свободного конца трубы.

Амплитуда динамической силы на уровне расположения второй массы при колебаниях по первой форме:

F₁(15) =F_{01× a 1}(15) = 2,661× 667/667 = 2,661 Н/м;

Находим момент в защемлении и прогиб верха трубы от статического действияF₁(5) иF₁(15):

М= 0,4× 10× 5 + 2,661× 10× 15 = 419,15 Нм.

f= 5,288 мм (получено из расчета по программе “ЛИРА” от статического действия ветровой нагрузки.

По формуле 31 /5/ резонансный момент и перемещение:

М^рез= p /d ×М^с= 3,14/0,15× 419,15 = 8778,66 Нм;

f^рез= p /d ×f^c= 3,14/0,15× 5,288 = 110,752 мм.

Далее определяются расчетные величины с учетом коэффициента надежности по ветровой нагрузке g_f= 1,4.

Пример 2.Расчет связевого каркаса жилого многоэтажного дома в районе проспекта Пушкина и улиц Притыцкого и Д. Сердича в г. Минске (пример передан инженером В.И. Ореховым, институт “Минскгражданпроект”).

Высота здания от верха фундаментной плиты до оси самого верхнего ригеля — 54,375 м. Размеры здания в плане приведены на рис. 4.

Машинный расчет каркаса выполнялся на 16 загружений:

1, 2 — постоянная нагрузка; 3 — временная длительно действующая; 4 — кратковременная снеговая; 5-8 — ветер в направлении осейOXиOY; 9-10 — ветер по диагонали здания; 11-16 — распределение весов масс для расчета на пульсационное воздействие ветра.

При определении ветровой нагрузки на горизонтальные элементы каркаса здания вначале рассчитывалась вертикальная неразрезная балка с числом пролетов, равным числу этажей, на действие горизонтального ветрового давления. Усилия в опорах неразрезной балки на уровне каждого междуэтажного перекрытия давали погонную ветровую нагрузку на крайние горизонтальные ригеля каркаса здания. При определении ветрового давления, направленного нормально диагоналям здания, менялся аэродинамический коэффициентсв формуле (3), и, следовательно, величинаw_m.

Нормы /5/ рекомендуют при определении частот и форм собственных колебаний рассматриваемого здания принимать вертикальный защемленный стержень с равномерно расположенными по высоте массами. Однако рассматриваемое здание с металлическими связями обладало большой горизонтальной податливостью, и следовало ожидать, что первыми формами колебаний будут изгибно-крутильные. Чтобы их не потерять, распределение массы здания на сосредоточенные производилось по следующему принципу. По разнице продольных сил от постоянной нагрузки в колоннах смежных этажей определялась величина массы междуэтажного перекрытия. Эта масса распределялась на 4 сосредоточенные в углах прямоугольного участка перекрытия. Так как здание имело почти симметричную форму в плане, то массы также распределялись симметрично на пересечениях осей 3-В, 3-Е, 5-В, 5-Е (рис. 4). Считалось, что каждая масса обладала тремя степенями свободы. На фундаментную плиту передавалась масса лифта. (В некоторых пакетах распределение весов масс автоматизировано.)

Вначале расчетом были определены частоты и формы собственных колебаний здания (модальный анализ). Распределение частот собственных колебаний здания дано в таблице.

№ п/п	Собственные значения	Частоты	Периоды
1/с	Гц	с
1	1,12391	0,8898	0,1417	7,0581
2	0,93918	1,0648	0,1695	5,8980
3	0,61304	1,6312	0,2597	3,8499
4	0,28435	3,5168	0,5600	1,7857
5	0,22767	4,3923	0,6994	1,4297
6	0,18950	5,2771	0,8403	1,1900
7	0,14412	6,9385	1,1049	0,9051
8	0,12513	7,9915	1,2725	0,7858
9	0,11271	8,8720	1,4127	0,7078
10	0,10800	9,2593	1,4774	0,6782
11	0,10445	9,5740	1,5245	0,6559
12	0,09980	10,0196	1,5995	0,6267
13	0,09883	10,1181	1,6112	0,6206
14	0,09825	10,1783	1,6208	0,6170
15	0,09301	10,7511	1,7120	0,5841
16	0,08701	11,4927	1,8300	0,5464
17	0,07675	13,0290	2,0747	0,4820
18	0,07584	13,1855	2,0996	0,4762
19	0,07369	13,5700	2,1608	0,4627
20	0,07203	13,8837	2,2108	0,4523
21	0,06880	14,5361	2,3145	0,4320
22	0,06424	15,5658	2,4786	0,4034
23	0,06355	15,7348	2,5055	0,3991
24	0,06188	16,1605	2,5733	0,3886
25	0,05975	16,7371	2,6651	0,3752
26	0,05529	18,0861	2,8799	0,3472
27	0,05473	18,2705	2,9093	0,3437

Из анализа данных таблицы следует, что при заполнении документа 15 исходных данных для машинного расчета по ПК “ЛИРА-Windows” необходимо учитывать 26 форм собственных колебаний здания (случай Г).

На рис. 5 показана в плане первая форма собственных колебаний каркаса рассчитываемого здания, из которой видно, что она является именно изгибно-крутильной, которая была бы не учтена при замене каркаса консольной вертикальной балкой для определения частот собственных колебаний.

Расчеты показали, что наиболее опасным оказалось диагональное воздействие ветра, что потребовало увеличения жесткостных параметров вертикальных связей в каркасе здания. Это, в свою очередь, потребовало повторного определения весов масс и выполнения модального анализа.

В процессе работы над статьей инженер С.Д. Минчук (ОАО “Белпроект”) указал авторам на необходимость учета временной длительно действующей нагрузки при определении весов масс (пример 2). Однако в предлагаемом расчете доля временной длительно действующей нагрузки составляла всего 14% от постоянной, что при расчете привело бы к уменьшению первых частот собственных колебаний приблизительно на 7%. В то же время нормы прямо не указывают, с каким коэффициентом сочетаний необходимо брать эту долю внешней нагрузки при определении весов масс. Поэтому, в принципе соглашаясь с замечанием С.Д. Минчука о необходимости двойного динамического расчета здания на стадии строительства до пуска отопления и в стадии эксплуатации со всеми сопутствующими временными нагрузками, авторы сочли возможным пренебречь влиянием временной длительно действующей нагрузки при расчете здания на пульсацию.

Авторы отдают себе отчет в том, что материал статьи далеко не в полной мере охватывает все случаи действия ветровой нагрузки на сооружение. Это невозможно сделать в силу многообразия встречающихся случаев расчета и учета такого сложного вида нагружения, как ветровое. Однако если содержание статьи поможет инженеру-проектировщику в его работе, то цель авторов будет достигнута.

Рис. 1. Зависимость скорости ветра от времени

Рис. 2. Обтекание сооружения ветровым потоком

Рис. 3. Расчетная схема дымовой трубы с распределением по высоте масс и нормативной средней составляющей ветрового давления

Рис. 4. План фундаментной плиты и разбивка осей здания

Рис. 5. Вид в плане элементов металлического каркаса при первой изгибно-крутильной форме колебаний здания.

1. СНиП 2.01.07-85*. Нагрузки и воздействия. М., 1986.
2. Савицкий Г.А. Ветровая нагрузка на сооружения. М.: Стройиздат, 1972.
3. Беспрозванная И.М., Соколов А.Г., Фомин Г.М. Воздействие ветра на высокие сплошностенные сооружения. М.: Стройиздат, 1976.
4. Симиу Э., Сканлан Р. Воздействие ветра на здания и сооружения. М.: Стройиздат, 1978.
5. Руководство по расчету зданий и сооружений на воздействие ветра. М.: Стройиздат, 1978.

Сергей БОСАКОВ, доктор техн. наук, профессор БНТУ,
Олег КАЛОША, главн. специалист института “Минскпроект”

Строительство и недвижимость. Статья была опубликована в номере 48 за 2003 год в рубрике наука

Источник

Богдан Новах

Эксперт по предмету «Архитектура и строительство»

Задать вопрос автору статьи

Собственные колебания

Собственные или свободные колебания – это колебания, происходящие в системе при отсутствии переменных внешних воздействий. Такие колебания возникают по причине начального отклонения одного из параметров от состояния равновесия.

В целом колебания представляют собой повторяющийся во времени процесс изменения состояния системы около точки равновесия (при колебании маятника все углы его отклонения от вертикали повторяются с определенной периодичностью.

В реальных макроскопических системах собственные колебания затухают по причине потерь энергии. Любой колебательный процесс связан с переходом энергии из одной формы в другую.

Следует заметить, что колебания различной физической природы имеют ряд общих закономерностей и тесно связаны с волнами. В этой связи исследованием таких закономерностей занимается теория колебаний и волн. Принципиальное отличие колебаний от волн заключается в том, что распространение последних сопровождается переносом, а не переходом энергии.

По характеру взаимодействия с окружающей средой колебания разделяют на:

вынужденные;
автоколебания;
параметрические;
собственные.

В настоящей статье речь пойдет о собственных колебаниях, т.е. о колебаниях системы под действием внутренних сил после выведения системы из равновесия.

При небольших отклонениях от состояния равновесия движение любой системы будет удовлетворять принципу суперпозиции. Согласно данному принципу сумма произвольных движений составляет допустимое движение системы. Подобные движения описываются линейными (дифференциальными) уравнениями.

В случае, если в системе нет потерь энергии (она консервативна), а ее параметры не изменяются во времени, то любое собственное колебание может быть представлено, как совокупность нормальных колебаний, изменяющихся во времени по закону синуса с определенными частотами собственных колебаний.

Если положение системы в любой момент времени описывается единственным параметром, то такая система имеет одну степень свободы. Идеальным примером такой системы является маятник, колеблющийся в плоскости. И действительно, положение маятника в любой момент может определяться лишь углом его отклонения от вертикали.

«Как определить собственную частоту колебаний» 👇

В природе существует большое количество весьма интересных систем, имеющих две степени свободы. Например, молекулы и элементарные частицы (наиболее примечательны нейтральные К-мезоны). Более простым и понятным примером является двойной маятник (один маятник подвешивается к опоре, второй – к гире первого маятника; два маятника, объединенные пружиной).

Чтобы описать состояние системы с двумя степенями свободы необходимо уже две переменные. Например, в случае со сферическим маятником роль таких переменных будут выполнять положения маятника в двух взаимно перпендикулярных плоскостях. В случае объединенных маятников эти переменные соответствуют положению каждого из маятников.

В общем виде движение системы, имеющей две степени свободы, может иметь весьма сложный вид, не напоминающий простое гармоническое движение.

Для двух степеней свободы, а также при линейных уравнениях движения общий вид движения представляет собой суперпозицию двух простейших гармонических зависимостей, происходящих в один момент. Эти два элементарных движения называют нормальными (собственными) колебаниями или гармониками.

Колебательные системы с сосредоточенными параметрами, состоящими из N связанных осцилляторов (например, цепочка из связанных между собой пружинками шариков), число гармоник будет равно N. В системах с распределенными параметрами (мембрана или резонатор) таких колебаний существует бесчисленное множество. Например, для закрепленной струны длиной L гармоники будут отличаться количеством полуволн, которые возможно уложить по всей длине струны. Если скорость распространения волн струны равна v, то спектр собственных частот определяется по формуле:

Рисунок 1. Формула 1. Автор24 — интернет-биржа студенческих работ

Наличие дисперсии волн искажает данное простое распределение частот, спектр которых определяется уже из дисперсионных уравнений.

Что касается реальных систем, то в них собственные колебания затухают из-за потерь энергии, поэтому их следует считать лишь приближенно гармоническими в интервале времени, меньшем $1/δ$. Затухающие колебания могут быть представлены в виде нескольких гармонических колебаний, непрерывно заполняющих определенный интервал частот, тем меньшим, чем меньше $δ$. В таком случае следует говорить о расширении спектральной линии, характеризуемой добротностью $Q$ и равной отношению запасенной энергии $W$ к потерям $P$. Отсюда следует, что отношение сгущение спектра из-за потерь энергии может повлечь за собой превращение дискретного спектра в сплошной при приближении ширины линий к интервалу между ними.

Колебания в нелинейных системах

Собственные колебания нелинейных систем не поддаются простой классификации. Нелинейность систем с дискретным спектром частот собственных колебаний приводят к переходу энергии по спектральным компонентам. При этом возникает явление конкуренции гармоник – выживание одних и подавление других.

Подобный процесс может стабилизировать дисперсия. Она может привести к появлению устойчивых пространственно-временных образований (например, солитоны).

Большое значение при возбуждении колебаний может иметь явление резонанса, которое заключается в резком увеличении амплитуды колебаний (отклика). Данное явление наблюдается при приближении частоты внешних воздействий на систему к некоторой резонансной частоте, которая характеризует настоящую систему.

Если система линейна и ее параметры находятся вне зависимости от времени, то резонансные частоты совпадают с частотой собственных ее колебаний. Отклик системы в данном случае будет усиливаться с увеличением добротности колебательной системы $Q$.

Раскачка будет происходить до тех пор, пока энергия, поступающая извне (например, полученная при отклонении маятника от положения равновесия) будет превышать потери за время осцилляции. Что касается линейных колебаний, то энергия, вносимая извне будет пропорциональна амплитуде, а потери будут расти пропорционально ее квадрату. Отсюда следует, что баланс энергии достижим во всех случаях.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Примеры задач частотного анализа

Определение собственных частот колебаний балки

Определение первой собственной частоты колебаний круглой пластинки

Свободные колебания сферического купола

Собственные колебания

Колебания в нелинейных системах