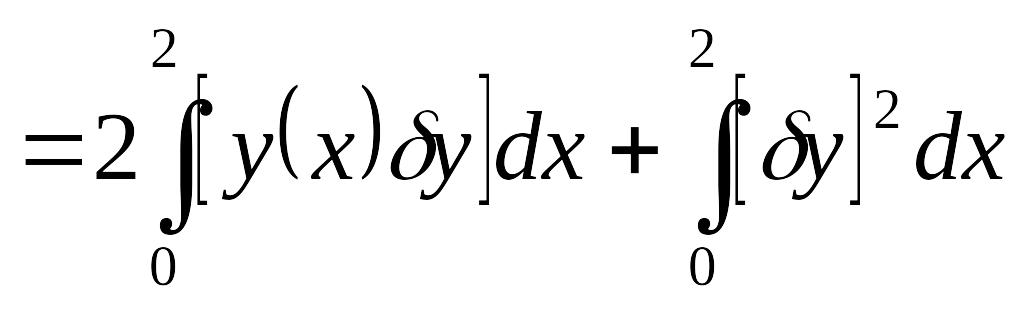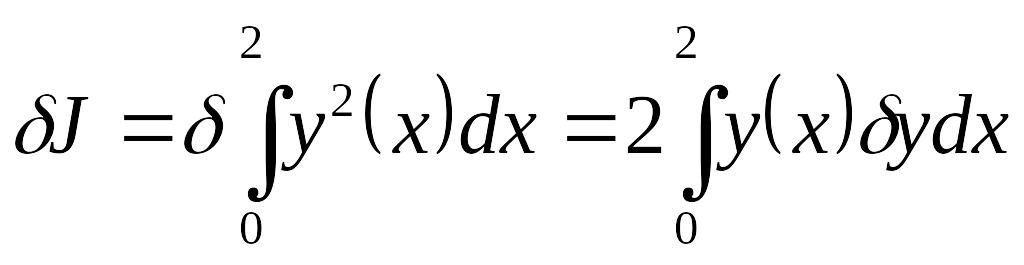Как найти первую вариацию

Вариационное исчисление: примеры и задачи

Вариационное исчисление для чайников

Древнейшей из задач на максимум и минимум является задача отыскания среди плоских замкнутных кривых заданной длины такую, которая охватывает наибольшую площадь (5 в до н.э.) — и это классическая изопериметрическая задача вариационного исчисления. Началось же классическое вариационное исчисление с задачи о кривой наискорейшего спуска (брахистохроне) в 1696 г. с публикации Иоганна Бернулли.

Общие принципы и методы решения задач вариационного исчисления были введены в 18 веке Эйлером и Лангранжем, они же установили тесную связь между ВИ и естествознанием. Далее на протяжении более чем двух столетий они разрабатывались, были найдены помимо необходимых условий первого порядка (уравнений Эйлера-Лагранжа) необходимые и достаточные услвоия второго порядка для сильных и слабых экстремумов.

На этой странице мы рассмотрим примеры с подробным решением следующих типов: простейшая задача вариационного исчисления, задача Больца, изопериметрическая задача, задача со старшими производными. А также научимся находить вариацию и допустимые экстремали функционала. Все это относится к классическому вариационному исчислению.

Смежные задачи вы можете найти в соответствующих разделах: Нелинейное программирование, Многокритериальная оптимизация, Математическое программирование и т.д.

Вариационное исчисление: задачи с решениями

Задача 1. Решить классическую задачу вариационного исчисления:

$$
int_0^1 dot{x}^2 dt to extr, quad x(0)=1, x(1)=0.
$$

Задача 2. Решить задачу Больца

$$
int_0^1 dot{x}^2 dt +alpha x^2(1) to extr, quad x(0)=1.
$$

Задача 3. Решить изопериметрическую задачу

$$
int_0^1 dot{x}^2 dt to extr, int_0^1 x^2 dt =3, quad x(0)=1, x(1)=6.
$$

Задача 4. Решить задачу со старшими производными

$$
int_0^pi (ddot{x}^2+4x^2) dt to extr, quad x(0) = dot x(0)=0, , dot x(pi)=sh(pi).
$$

Задача 5. Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям

$$
J(y)=int_0^1 (e^y +xy’)dx, quad y(0)=0, y(1)=1.
$$

Задача 6. Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям

$$
J(y)=int_0^1 e^{-x}cdot y» ^2 dx, quad y(0)=0, y'(0)=1, y(1)=e, y'(1)=2e.
$$

Задача 7. Для указанной вариационной задачи записать уравнение Эйлера и найти экстремаль, удовлетворяющую условиям $y(0) = 19, y(1)=30$

$$int_0^1 (1+y’^2)dx.$$

Задача 8. Найти вариацию функционала

$$int_0^1 (x+y’)ln sin y’ dx.$$

Задача 9. Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям

$$
J(y)=int_0^{pi/4} (4ysin x +y’^2-y^2)dx, quad y(0)=0, y(pi/4)=0.
$$

Консультации и помощь

Нужно выполнить контрольную работу или задачи по вариационному исчислению и смежным предметам? Нет проблем! Стоимость консультации по решению — от 150 рублей, подробное оформление согласно требованиям методички в Word.

Полезные ссылки

• Вариационное исчисление: задачи, алгоритмы, примеры Крайне удобная для решения задач методичка: для каждого типа задач есть теория, краткий алгоритм и пример решения нескольких задач. Рекомендуем.
• Вариационное исчисление и основы теории управления Краткое учебное пособие с примерами задач по ВИ
• Эльсгольц Л.Э. Вариационное исчисление Классический учебник, теория изложена на простом уровне, множество разобранных примеров по каждому разделу.
• Изопериметрическая задача: теория и примеры решения

      
Рассмотрим функционал вида

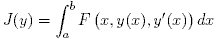
(1)

      
Предположим, что  F  — заданная функция всех трех аргументов, имеющая непрерывные производные до второго порядка
включительно на множестве  a ≤ x ≤ b,
 –∞ < y, y‘ < +∞.

      
В качестве области определения функционала возьмем класс функций  y = f (x)  на
отрезке  [a, b], удовлетворяющих граничным условиям

      
и принадлежащих множеству функций на  [a, b], имеющих непрерывные производные первого порядка
(это множество обозначается  C⁽¹⁾ [a, b]).

      
Определение. Говорят, что функционал (1) достигает относительный минимум (максимум) для кривой
 y₀(x)  из класса  C⁽¹⁾ [a, b],
удовлетворяющей граничному условию (2), если

J(y) ≥ J(y₀)           
( J(y) ≤ J(y₀) )

      
для любых других кривых класса  С⁽¹⁾, удовлетворяющих (2) и достаточно близких к функции
 y₀ = f₀ (x)  в том смысле, что для некоторого
 ε > 0  ыполняются неравенства

      
Выведем необходимые условия, которым должна подчиняться функция  y₀(x)  для того, чтобы
функционал  J (y)  достигал максимума или минимума для  y₀(x).

Пусть  y = f (x)  – функция из
 C⁽¹⁾ [a, b]), удовлетворяющая (2). Возьмем любую функцию
 η(x)  из  C⁽¹⁾ [a, b])  такую, что
 η(a) = η(b) = 0.

Образуем новую функцию  y(x) + α η(x)  и, подставляя ее в функционал
 J (y), получим функцию параметра  α

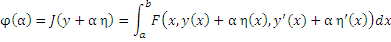
(3)

      
Определение. Если существует производная

      
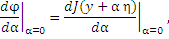
то она называется первой вариацией функционала  J (y) и обозначается
 δJ (y, h).

---

2.1. Приращения (вариация) аргумента функционала

Вариация аргумента функционала вводится
по аналогии с приращением

аргумента функции f(x).
А именно,

Определение 1. приращением или
вариацией


аргумента y(x)
функционала

называется разность между двумя функциями

.
При этом предполагается, что y(x)
меняется произвольно в некотором классе
функций.

Определение 2. Функционал

называется непрерывным, если малому
изменению y(x)
соответствует малое изменение функционала

.

Данное определение аналогично определению
непрерывности функции f(x):
малому изменению x,
соответствует малое изменение функции
f(x).

Здесь следует уточнить, какие изменения
функции y(x),
являющейся аргументом функционала,
считаются малыми или когда кривые

и

считаются близкими.

Можно считать близкими функции

и

в том случае, если

мал для всех значений x,
для которых задаются функции

и

.
Это значит, что соответствующие кривые
близки по ординатам.

Однако при таком определении близости
кривых часто встречаемые в приложениях
функционалы вида

из-за наличия в подынтегральной функции
аргумента

очень редко будут непрерывными. Поэтому
во многих случаях естественно считать
близкими только те кривые, которые
близки по ординатам и по направлению
касательных в соответствующих точках,
т.е. требуется, чтобы были малы модули
разностей не только функций

,
но и производных

.
Иногда требуется малость модуля разностей
производных более высоких порядков.

Поэтому вводят следующие определения
близости кривых

и

.

Кривые

и

называются близкими, в смысле близости
нулевого порядка, если модуль разности

мал.

Кривые

и

близки в смысле близости первого порядка,
если модули разностей

и

малы. Кривые

,

близки в смысле к-го порядка, если модули
разностей

;

;
…;

малы.

Н
а
рис. 4 изображены кривые, близкие в смысле
близости нулевого порядка, но не близкие
в смысле близости первого порядка, так
как ординаты у них близки, а направления
касательных не близки. На рис. 5 изображены
кривые, близкие в смысле близости первого
порядка.

Из этих определений следует, что если
кривые близки в смысле к-го порядка, то
они тем более близки в смысле близости
любого меньшего порядка.

2.2. Вариация функционала

Линейным функционалом называется
функционал

,

удовлетворяющий следующим условиям:

и

где с – производная постоянная.

Примером линейного функционала является

Для функций: линейной функцией называется
функция

,
удовлетворяющая следующим условиям:

и

.

Линейная функция одной переменной имеет
вид

,
где k-постоянная.

Вариация функционала при изучении
нелинейных функционалов играет ту же
роль, что понятие дифференциала при
изучении нелинейных функций. Если
приращение функции

может быть представлено в виде

,

где

не зависит от

,
а

при

,
то функция

называется дифференцируемой, а линейная
по отношению к

часть приращения

называется дифференциалом функции

.
Разделив на

и переходя к пределу при

,
получим, что

и, следовательно,

.

Определение. Если приращение
функционала

можно представить в виде

,
(1)

где

-линейный
по отношению к

функционал,

-максимальное
значение

и

при

,
то

называется вариацией функционала и
обозначается

.
Если для краткости обозначить второе
слагаемое в (1) через

,
то

,
(2)

Таким образом, вариация нелинейного
функционала равна главной линейной
части его приращения. Замена приращения
на вариацию означает линеаризацию
функционала при переходе от одной
функции

к другой, близкой функции

.

Здесь

-произвольная
функция, мало уклоняющаяся от нуля и
добавляемая к исходной функции

для получения новой функции (рис. 6).

Пример 1. Дан функционал

.
Найти его вариацию.

Решение. При переходе от

к

функционал получит приращение

.

При фиксированной функции

функционал состоит из двух частей.
Каждая из этих частей представляет
собой функционал относительно

.
Первое слагаемое есть линейный функционал
относительно

,
а второе слагаемое при малых

имеет высший порядок малости. Таким
образом,

.

В конкретных задачах вариация функционалов
вычисляется с помощью формулы Тейлора.
Так, для функционала вида

,
(3)

где при интегрировании считается

,
имеет

.
(*)

Т.к.

высшего порядка, то подставляя в (*) и
отбрасывая эти члены, получим

.
(4)

Для функционала

(5)

аналогично получаем

,
(6)

где

можно понимать и как

,
и как

,
т.к.

(производная от разности двух функций
равна разности производных).

Действительно,

высшего порядка.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #