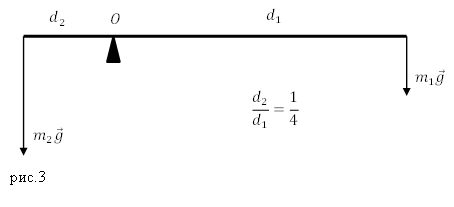Простейшие механизмы. Рычаг
Можно ли поднять земной шар?
Выдающийся древнегреческий учёный Архимед более (2000) лет назад ответил примерно так:
Дайте мне точку опоры, и я подниму земной шар.
Простейшим механизмом, при помощи которого можно поднять тяжёлые предметы, является рычаг.
Рычаг состоит из перекладины, рычага и опоры.
Точка опоры перекладину рычага делит на два плеча рычага.
Точка опоры может быть расположена между плечами рычага ((1)) или по одну сторону от плеч рычага ((2)).
Рис. (1). Изображение рычага в двух вариантах расположения точки опоры
Рычаг находится в равновесии, если произведение силы на плечо по обе стороны опоры одинаково:
Из условия равновесия рычага следует, что если рычаг находится в равновесии, тогда приложенные силы обратно пропорциональны длине плеч рычага:
Рис. (2). Изображение рычага в равновесном состоянии
Используя рычаг, можно поднимать тяжёлые предметы, прикладывая небольшое усилие.
Величина экономии силы одинакова с соотношением длин более длинного и более короткого плеча рычага.
В обиходе часто используют рычаги. Например, ножницы, плоскогубцы, лопата, тачка являются примером использования рычагов.
Рис. (3). Изображение плоскогубцев
Источники:
Рис. 1. Изображение рычага в двух вариантах расположения точки опоры. © ЯКласс.
Рис. 2. Изображение рычага в равновесном состоянии. © ЯКласс.
Рис. 3. Изображение плоскогубцев. © ЯКласс.
С древних времен люди используют различные устройства для совершения механической работы. Эти устройства позволяют поднимать груза большой массы или перемещать их. Они называются простыми механизмами.
Например, еще в Древнем Египте (около трех тысяч лет назад) использовали рычаги (рисунок 1). С их помощью передвигали и поднимали на большую высоту огромные каменные плиты.
На данном уроке мы рассмотрим этот механизм и его устройство. Именно рычаг дает возможность приложить меньшую силу, чем потребовалось бы без него. По этой причине рычаги присутствуют в составе сложных машин и устройств и в современном мире.
Устройство рычага
Что представляет собой рычаг?
Рычаг — это любое твердое тело, которое может вращаться вокруг неподвижной опоры.
Взгляните на рисунок 2. В данном случае Образавр использует в качестве рычага обычную палку, чтобы поднять тяжелый камень.
Камень действует на рычаг с некоторой силой — весом $P$. Для того чтобы его поднять, необходимо преодолеть этот вес, направленный вертикально вниз. В первом случае (рисунок 2, а) Образавр давит на конец палки с силой $F$, а во втором (рисунок 2, б) — поднимает конец палки.
В обоих случаях у этого рычага есть неподвижная точка опоры — точка О. Через нее проходит воображаемая ось, вокруг которой может поворачиваться рычаг.
Сила, с которой Образавр действует на палку (рычаг), меньше веса камня, но тем не менее у него получается сдвинуть этот камень. Это говорит о том, что с помощью рычага человек получает выигрыш в силе.
Виды рычагов
Таким образом, рычаги бывают двух видов (рисунок 3):
- Рычаг 1-го рода — силы приложены по разные стороны от точки опоры O (рисунок 3, а);
- Рычаг 2-го рода — силы приложены по одну сторону от точки опоры O (рисунок 3, б).
Рисунок 3 является схематическим изображением рычагов, показанных на рисунке 2.
Плечо силы рычага
На рисунке 4 изображен рычаг. Его точки A и B — это точки приложения сил $F_1$ и $F_2$ соответственно. Точка опоры O расположена между точками A и B — значит, перед нами рычаг 1-го рода.
А теперь взгляните на схему этого рычага (рисунок 4). Силы $F_1$ и $F_2$ направлены в одну сторону.
Длина отрезка OA обозначена как $l_1$, а длина отрезка OB — $l_2$. Эти величины называются плечом силы.
Что называют плечом силы?
Плечо силы — это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.
Как найти плечо силы?
Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы. Длина этого перпендикуляра и есть плечо данной силы.
Тогда, OA или $l_1$ — это плечо силы $F_1$, а OB или $l_2$ — плечо силы $F_2$.
Условие равновесия рычага
Чтобы получить условие равновесия рычага, нужно провести опыты. К рычагу по обе стороны от точки опоры подвешиваются разные груза так, чтобы каждый раз рычаг оставался в равновесии. В каждом случае измеряются модули сил и их плечи. В нашем случае (рисунок 4) видно, что сила $2 space Н$ уравновешивает силу $4 space Н$. А плечо меньшей силы в 2 раза больше плеча большей силы.
С помощью таких опытов было установлено правило равновесия рычага.
В чем состоит правило равновесия рычага?
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил:
$frac{F_1}{F_2} = frac{l_2}{l_1}$,
где $F_1$ и $F_2$ — силы, которые действуют на рычаг, $l_1$ и $l_2$ — плечи этих сил.
Кто установил правило равновесия рычага?
Это правило было установлено Архимедом еще в III веке до н. э. Иногда правило равновесия рычага так и называют — правило Архимеда. Легенда гласит, что после этого открытия Архимед воскликнул: «Дайте мне точку опору, и я переверну Землю!».
Из правила равновесия следует, что меньшей силой можно уравновесить большую силу при помощи рычага.
Например, возьмем рычаг, у которого одно плечо будет в 2 раза больше другого (как на рисунке 4). Приложим к точке A силу в $100 space Н$. Тогда в точке B мы сможем уравновесить силу в $200 space Н$ (в 2 раза большую). Если нам нужно поднять более тяжелый груз, то можно увеличить плечо рычага $l_1$, к которому мы прикладываем силу.
Примеры задач
Задача №1
Рабочий поднимает груз массой $300 space кг$ c помощью рычага 1-го рода. Большее плечо силы рано $3 space м$, а меньшее — $0.6 space м$. Какую силу рабочий прикладывает к большему плечу рычага?
Дано:
$m = 300 space кг$
$l_1 = 3 space м$
$l_2 = 0.6 space м$
$g = 9.8 frac{Н}{кг}$
$F_1 — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем правило равновесия рычага:
$frac{F_1}{F_2} = frac{l_2}{l_1}$.
Выразим отсюда силу $F_1$, которую прикладывает к рычагу рабочий:
$F_1 = F_2 cdot frac{l_2}{l_1}$.
Сила $F_2$ — это вес груза $P$, который мы можем рассчитать формуле: $P = gm$. Подставим в нашу формулу и рассчитаем силу $F_1$:
$F_1 = F_2 cdot frac{l_2}{l_1} = gm cdot frac{l_2}{l_1} = 9.8 frac{Н}{кг} cdot 300 space кг cdot frac{0.6 space м}{3 space м} = 2940 space Н cdot 0.2 = 588 space Н$.
Ответ: $F_1 = 588 space Н$.
Задача №2
На рисунке 7 схематически изображен рычаг. Точка опоры находится в точке O. Одно деление на шкале рычага равно $10 space см$. Какую массу должен иметь груз, подвешенный в точке A, чтобы рычаг находился в равновесии?
Дано:
$m_1 = 100 space г$
$m_2 = 200 space г$
$l_1 = 40 space см$
$l_2 = 20 space см$
$g = 9.8 frac{Н}{кг}$
СИ:
$m_1 = 0.1 space кг$
$m_2 = 0.2 space кг$
$l_1 = 0.4 space м$
$l_2 = 0.2 space м$
$m_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Найдем силу, которая будет действовать на рычаг в точке B. Эта сила будет равна весу $P_2$, с которым груза массой $m_1$ и $m_2$ действуют на подвес. Обозначим эту силу $F_2$.
$F_2 = P_2 = gm = g(m_1 + m_2) = 9.8 frac{Н}{кг} cdot (0.1 space кг + 0.2 space кг) = 9.8 frac{Н}{кг} cdot 0.3 space кг approx 3 space Н$.
Запишем правило равновесия рычага:
$frac{F_1}{F_2} = frac{l_2}{l_1}$.
Выразим отсюда и рассчитаем силу $F_1$, с которой будет действовать на рычаг груз неизвестной массы:
$F_1 = frac{F_2 cdot l_2}{l_1} = frac{3 space Н cdot 0.2 space м}{0.4 space м} = 1.5 space Н$.
Сила $F_1$ будет равна весу $P_1$, с которым груз массой $m_3$ действуют на подвес:
$F_1 = P_1 = gm_3$.
Найдем массу груза:
$m_3 = frac{F_1}{g} = frac{1.5 space Н}{9.8 frac{Н}{кг}} approx 0.15 space кг = 150 space г$.
Ответ: $m_3 = 150 space г$.
Формула плеча силы в физике
Формула плеча силы
Определение и формула плеча силы
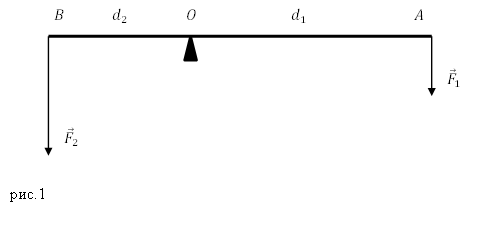
Рассмотрим рычаг с осью вращения находящийся в точке О. (рис.1). Силы ${overline{F}}_1$ и ${overline{F}}_2$, действующие на рычаг направлены в одну сторону.
Минимальное расстояние между точкой опоры (точка О) и прямой, вдоль которой действует на рычаг сила, называют плечом силы.
Для нахождения плеча силы следует из точки опоры опустить перпендикуляр к линии действия силы. Длинна данного перпендикуляра и станет плечом рассматриваемой силы. Так, на рис.1 расстояние $left|OAright|=d_1$- плечо силы $F_1$; $left|OAright|=d_2$- плечо силы $F_2$.
Рычаг находится в состоянии равновесия, если выполняется равенство:
[frac{F_1}{F_2}=frac{d_2}{d_1}left(1right).]
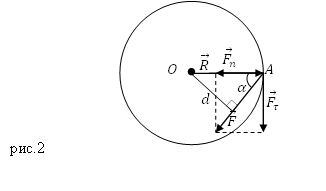
Предположим, что материальная точка движется по окружности (рис.2) под действием силы $overline{F}$ (сила действует в плоскости движения точки). В таком случае угловое ускорение ($varepsilon $) точки определяется тангенциальной составляющей ($F_{tau }$) силы $overline{F}$:
[mRvarepsilon =F_{tau }left(2right),]
где $m$ — масса материальной точки; $R$ — радиус траектории движения точки; $F_{tau }$ — проекция силы на направление скорости движения точки.
Если угол $alpha $ — это угол между вектором силы $overline{F}$ и радиус — вектором $overline{R}$, определяющим положение рассматриваемой материальной точки (Этот радиус- вектор проведен из точки О в точку А на рис.2), тогда:
[F_{tau }=F{sin alpha left(3right). }]
Расстояние $d$ между центром O и линией действия силы $overline{F}$ называют плечом силы. Из рис.2 следует, что:
[d=R{sin alpha left(4right). }]
Если на точку будет действовать сила ($overline{F}$), направленная по касательной к траектории ее движения, то плечо силы будет равно $d=R$, так как угол $alpha $ станет равен $frac{pi }{2}$.
Момент силы и плечо
Понятие плечо силы иногда используют, для записи величины момента силы ($overline{M}$), который равен:
[overline{M}=left[overline{r}overline{F}right]left(5right),]
где $overline{r}$ — радиус — вектор проведенный к точке продолжения силы$ overline{F}$. Модуль вектора момента силы равен:
[M=F{rsin alpha = }Fd left(6right).]
Построение плеча силы
И так, плечом силы называют длину перпендикуляра, который проводят из некоторой выбранной точки, иногда ее называют полюсом (выбираемой произвольно, но при рассмотрении одной задачи один раз). При рассмотрении задач точку О выбирают обычно на пересечении нескольких сил) к силе (рис.3 (а)). Если точка О будет лежать на одной прямой с силами или на самой силе, то плечи сил будут равны нулю.
Если перпендикуляр не получается построить, то вектор силы продлевают в нужном направлении, после этого строят перпендикуляр (рис.3 (б)).
Примеры задач с решением
Пример 1
Задание. Какова масса меньшего тела ($m_1$), если его уравновешивает тело массой $m_2={rm 2 }$кг? Тела находятся на невесомом рычаге (рис.3) отношение плеч рычага 1:4?
Решение. Основой решения задачи является правило равновесия рычага:
[frac{F_1}{F_2}=frac{d_2}{d_1}left(1.1right),]
где силы, действующие на концы рычага равны по модулю силам тяжести, которые действуют на тела, следовательно, формулу (1.1) перепишем в виде:
[frac{m_1g}{m_2g}=frac{d_2}{d_1}to frac{m_1}{m_2}=frac{d_2}{d_1}left(1.2right).]
Из выражения (1.2) получим искомую массу $m_1$:
[m_1=frac{m_2d_2}{d_1}.]
Вычислим искомую массу:
[m_1=2cdot frac{1}{4}=0,5 (кг).]
Ответ. $m_1=0,5 кг$
Пример 2
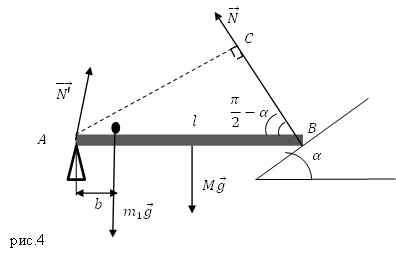
Задание. Однородный стержень длинной $l $и массой $M$ расположен горизонтально. Один конец стержня в точке А закреплён так, что может вращаться вокруг этой точки, другой конец опирается на наклонную плоскость, угол наклона которой к горизонту равен $alpha $. На стержне на расстоянии $b $от точки А лежит небольшой груз. Каковы плечи сил, действующих на стержень?
Решение. Изобразим на рис.4 силы, действующие на стержень. Это: сила тяжести: $Moverline{g}$, вес груза, расположенного на нем $overline{P}=m_1overline{g}$, сила реакции наклонной плоскости: $overline{N}$; сила реакции опоры в точке A: $overline{N}’$.
Плечи сил будем искать относительно точки A. Плечо силы $overline{N’}$ будет равно нулю, так как сила приложена к стержню в точке А:
[d_{N’}=0 left(2.1right).]
Плечо другой силы реакции опоры ($overline{N}$) равно длине перпендикуляра AC:
[d_N=l{sin (90-alpha ) }=l{cos alpha left(2.2right). }]
Плечо силы $Moverline{g}$ из рис.4 , так как сила тяжести приложена к центру масс стержня, который для однородного стержня находится на его середине:
[d_{Mg}=frac{l}{2}left(2.3right).]
Плечо силы $m_1overline{g},$ учитывая, что груз маленький и принимая его за материальную точку, равно:
[d_{m_1g}=b.]
Ответ. $d_{N’}=0;; d_N=l{sin (90-alpha ) }=l{cos alpha left(мright), }d_{Mg}=frac{l}{2}, d_{m_1g}=b$
Читать дальше: формула полезной мощности.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
- Учебники
- 7 класс
- Физика 👍
- Перышкин
- №3
авторы: Перышкин.
издательство: «Дрофа»
Раздел:
- ГЛАВА 4. Работа и мощность. Энергия
- §58. Рычаг. Равновесие сил на рычаге
- Вопросы
Как найти плечо силы?
reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. §58. Вопросы. Номер №3
Решение
Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы. Длина этого перпендикуляра и будет плечом данной силы.
рис. 168. Графическое изображение рычага с осью вращения
(OA — плечо силы F1; OB — плечо силы F2).
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Инфоурок
›
Физика
›Презентации›Решение задач по теме «Рычаг. Простые механизмы»
Решение задач по теме «Рычаг. Простые механизмы»
Скачать материал

Скачать материал


- Сейчас обучается 43 человека из 24 регионов


- Сейчас обучается 485 человек из 70 регионов


- Сейчас обучается 71 человек из 42 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Решение задач по теме «Простые механизмы»
Физика
7 класс -
2 слайд
Проверка
Что представляет собой рычаг?Что называют плечом силы?
В чем состоит правило равновесия рычага?
От каких двух величин зависит совершенная работа?
Что принимают за единицу работы?Рычаг — твердое тело, имеющее неподвижную ось вращения, на которое действуют силы, стремящиеся повернуть его вокруг этой оси.
Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.
Совершенная работа зависит от приложенной силы и от пройденного пути.
Единица работы – джоуль (Дж) -
3 слайд
Повторение
6. Как найти плечо силы?7. Что называют моментом силы?
8. В чем суть правила моментов?
Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.
Момент силы — это произведение модуля силы , вращающей тело, на её плечо.
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки. -
4 слайд
Задача 1
Плечи рычага равны 5 и 10 см. На меньшее плечо рычага действует сила, равная 2 Н. Какая сила действует на большее плечо рычага ? -
5 слайд
Проверка
Дано:
11 =5 см =0,05 м
12 =10 см =0,1 м
F1 = 2 Н
F2 — ?
Решение:Ответ: 1 Н.
-
6 слайд
Задача 2
Определите силу, которая приложена в точке А, если длина рычага 20 см и он находится в равновесии -
7 слайд
Проверка
Дано:
1 =20 см =0,2 м
11 =5 см =0,05 м
F1 = 1,5 Н
F2 — ?Решение
М1 = М2
Ответ: 0,5 Н
-
8 слайд
Задача 3
С помощью подвижного блока рабочий поднял контейнер на высоту 4 м, прилагая к свободному концу веревки силу 600 Н. Какую работу он совершил? -
9 слайд
Дано:
h =4 м
F = 600 Н
А — ?
Решение:
т.к. блок подвижный, то он даёт выигрыш в силе в 2 раза, значит вес груза в 2 раза больше силы рабочего:
Р = 2·F
А = Р·h
А = 2·F·h
А = 2·600 ·4 = 4800 Джh
-
10 слайд
Задача 4
Груз поднимают с помощью подвижного блока весом 40 Н, прикладывая к веревке силу 0,23 кН. Определите вес груза. -
11 слайд
Анализ задачи
Какой выигрыш в силе дает подвижный блок?
Выигрыш в силе будет в 2 раза.
Если бы блок был невесом, то какой вес им можно было бы поднять?
Вдвое больше силы рабочего.
Но блок сам весит 40 Н. Как тогда определить какой вес остается для груза ?
Отнимаем от полученной величины вес самого блока.
? -
12 слайд
Дано:
Рб= 40 Н
F = 0,23 кН = 230 Н
Рг = ?Решение:
Р = 2·F
Р = 2·230 = 460 (Н)
Р = Рб + Рг
Рг = Р – Рб
Рг = 460 — 40 = 420 (Н)
Ответ: 420 Н -
13 слайд
Итоги
Сегодня мы с вами закрепили знания по теме «Простые механизмы»:
Вспомнили, что рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил:и правила моментов:
И что подвижный блок, даёт выигрыш в силе в 2 раза.
Формулу совершенной работы А = F·s -
14 слайд
Рефлексия
Урок полезен, все понятно.
Лишь кое-что чуть-чуть неясно.
Еще придется потрудиться.
Да, трудно все-таки учиться! -
15 слайд
Домашние задание:
Повторить § 57 — 62, решить задачи из сборника Лукашик №766,771.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 266 291 материал в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы
Задачи к уроку КПД
- Учебник: «Физика», Перышкин А.В.
- Тема: §65 Коэффициент полезного действия механизма
- 23.06.2022
- 133
- 8


- 23.06.2022
- 170
- 5

- 22.06.2022
- 84
- 0




- 22.06.2022
- 664
- 11

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»
-
Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
-
Курс повышения квалификации «Основы управления проектами в условиях реализации ФГОС»
-
Курс профессиональной переподготовки «Клиническая психология: организация реабилитационной работы в социальной сфере»
-
Курс повышения квалификации «Экономика: инструменты контроллинга»
-
Курс повышения квалификации «Разработка бизнес-плана и анализ инвестиционных проектов»
-
Курс повышения квалификации «Организация маркетинга в туризме»
-
Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
-
Курс повышения квалификации «Методы и инструменты современного моделирования»
-
Курс профессиональной переподготовки «Организация деятельности специалиста оценщика-эксперта по оценке имущества»
-
Курс профессиональной переподготовки «Стратегическое управление деятельностью по дистанционному информационно-справочному обслуживанию»
-
Скачать материал
-
23.06.2022
3613
-
PPTX
1 мбайт -
133
скачивания -
Рейтинг:
5 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Орловская Ирина Владимировна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 7 лет и 6 месяцев
- Подписчики: 0
- Всего просмотров: 18870
-
Всего материалов:
20