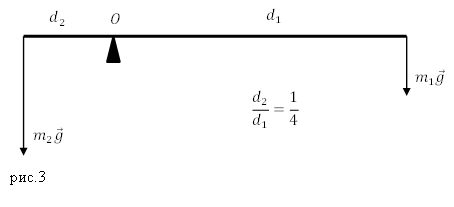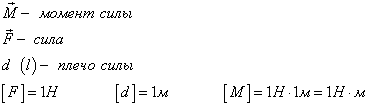Формула плеча силы в физике
Формула плеча силы
Определение и формула плеча силы
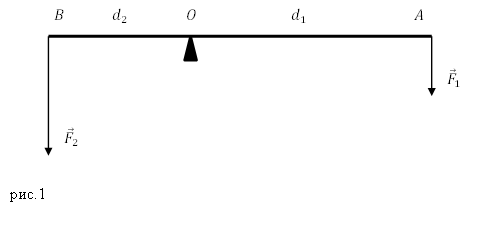
Рассмотрим рычаг с осью вращения находящийся в точке О. (рис.1). Силы ${overline{F}}_1$ и ${overline{F}}_2$, действующие на рычаг направлены в одну сторону.
Минимальное расстояние между точкой опоры (точка О) и прямой, вдоль которой действует на рычаг сила, называют плечом силы.
Для нахождения плеча силы следует из точки опоры опустить перпендикуляр к линии действия силы. Длинна данного перпендикуляра и станет плечом рассматриваемой силы. Так, на рис.1 расстояние $left|OAright|=d_1$- плечо силы $F_1$; $left|OAright|=d_2$- плечо силы $F_2$.
Рычаг находится в состоянии равновесия, если выполняется равенство:
[frac{F_1}{F_2}=frac{d_2}{d_1}left(1right).]
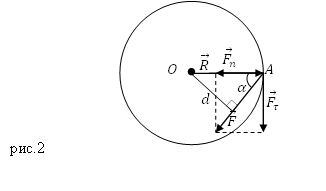
Предположим, что материальная точка движется по окружности (рис.2) под действием силы $overline{F}$ (сила действует в плоскости движения точки). В таком случае угловое ускорение ($varepsilon $) точки определяется тангенциальной составляющей ($F_{tau }$) силы $overline{F}$:
[mRvarepsilon =F_{tau }left(2right),]
где $m$ — масса материальной точки; $R$ — радиус траектории движения точки; $F_{tau }$ — проекция силы на направление скорости движения точки.
Если угол $alpha $ — это угол между вектором силы $overline{F}$ и радиус — вектором $overline{R}$, определяющим положение рассматриваемой материальной точки (Этот радиус- вектор проведен из точки О в точку А на рис.2), тогда:
[F_{tau }=F{sin alpha left(3right). }]
Расстояние $d$ между центром O и линией действия силы $overline{F}$ называют плечом силы. Из рис.2 следует, что:
[d=R{sin alpha left(4right). }]
Если на точку будет действовать сила ($overline{F}$), направленная по касательной к траектории ее движения, то плечо силы будет равно $d=R$, так как угол $alpha $ станет равен $frac{pi }{2}$.
Момент силы и плечо
Понятие плечо силы иногда используют, для записи величины момента силы ($overline{M}$), который равен:
[overline{M}=left[overline{r}overline{F}right]left(5right),]
где $overline{r}$ — радиус — вектор проведенный к точке продолжения силы$ overline{F}$. Модуль вектора момента силы равен:
[M=F{rsin alpha = }Fd left(6right).]
Построение плеча силы
И так, плечом силы называют длину перпендикуляра, который проводят из некоторой выбранной точки, иногда ее называют полюсом (выбираемой произвольно, но при рассмотрении одной задачи один раз). При рассмотрении задач точку О выбирают обычно на пересечении нескольких сил) к силе (рис.3 (а)). Если точка О будет лежать на одной прямой с силами или на самой силе, то плечи сил будут равны нулю.
Если перпендикуляр не получается построить, то вектор силы продлевают в нужном направлении, после этого строят перпендикуляр (рис.3 (б)).
Примеры задач с решением
Пример 1
Задание. Какова масса меньшего тела ($m_1$), если его уравновешивает тело массой $m_2={rm 2 }$кг? Тела находятся на невесомом рычаге (рис.3) отношение плеч рычага 1:4?
Решение. Основой решения задачи является правило равновесия рычага:
[frac{F_1}{F_2}=frac{d_2}{d_1}left(1.1right),]
где силы, действующие на концы рычага равны по модулю силам тяжести, которые действуют на тела, следовательно, формулу (1.1) перепишем в виде:
[frac{m_1g}{m_2g}=frac{d_2}{d_1}to frac{m_1}{m_2}=frac{d_2}{d_1}left(1.2right).]
Из выражения (1.2) получим искомую массу $m_1$:
[m_1=frac{m_2d_2}{d_1}.]
Вычислим искомую массу:
[m_1=2cdot frac{1}{4}=0,5 (кг).]
Ответ. $m_1=0,5 кг$
Пример 2
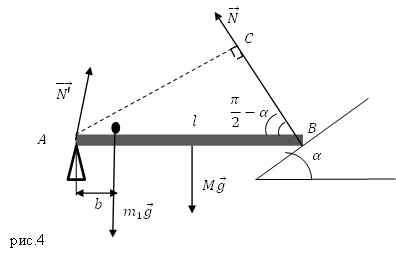
Задание. Однородный стержень длинной $l $и массой $M$ расположен горизонтально. Один конец стержня в точке А закреплён так, что может вращаться вокруг этой точки, другой конец опирается на наклонную плоскость, угол наклона которой к горизонту равен $alpha $. На стержне на расстоянии $b $от точки А лежит небольшой груз. Каковы плечи сил, действующих на стержень?
Решение. Изобразим на рис.4 силы, действующие на стержень. Это: сила тяжести: $Moverline{g}$, вес груза, расположенного на нем $overline{P}=m_1overline{g}$, сила реакции наклонной плоскости: $overline{N}$; сила реакции опоры в точке A: $overline{N}’$.
Плечи сил будем искать относительно точки A. Плечо силы $overline{N’}$ будет равно нулю, так как сила приложена к стержню в точке А:
[d_{N’}=0 left(2.1right).]
Плечо другой силы реакции опоры ($overline{N}$) равно длине перпендикуляра AC:
[d_N=l{sin (90-alpha ) }=l{cos alpha left(2.2right). }]
Плечо силы $Moverline{g}$ из рис.4 , так как сила тяжести приложена к центру масс стержня, который для однородного стержня находится на его середине:
[d_{Mg}=frac{l}{2}left(2.3right).]
Плечо силы $m_1overline{g},$ учитывая, что груз маленький и принимая его за материальную точку, равно:
[d_{m_1g}=b.]
Ответ. $d_{N’}=0;; d_N=l{sin (90-alpha ) }=l{cos alpha left(мright), }d_{Mg}=frac{l}{2}, d_{m_1g}=b$
Читать дальше: формула полезной мощности.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
I. Механика
Тестирование онлайн
Плечо силы
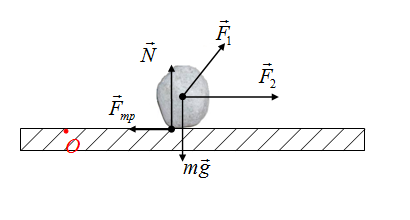
Плечо силы — это длина перпендикуляра из некоторой вымышленной точки О к силе. Вымышленный центр, точку О, будем выбирать произвольно, моменты каждой силы определяем относительно этой точки. Нельзя для определения моментов одних сил выбрать одну точку О, а для нахождения моментов других сил выбрать ее в другом месте!
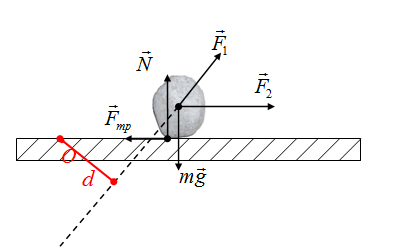
На камень действуют сила тяжести, сила трения, сила реакции опоры, две дополнительные внешние силы F1 и F2
Выбираем точку О в произвольном месте, больше ее местоположение не изменяем. Тогда плечо силы тяжести — это длина перпендикуляра (отрезок d) на рисунке
Плечо силы реакции опоры определяется аналогично
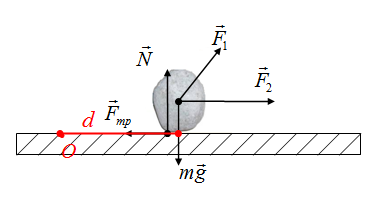
Если перпендикуляр нет возможности построить, то вектор силы продлевается в необходимом направлении, после чего строим перпендикуляр к этой линии. Плечо силы F2
Плечо силы F1
Осталась сила трения! Если точка О и сила лежат на одной линии, то плечо этой силы равно нулю. Плечо силы трения равно нулю.
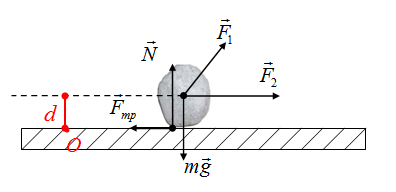
При решении задач выгодно точку О выбирать в точке пересечения нескольких сил. Тогда плечи всех этих сил будут нулевыми. Например, если точку О в предыдущем примере выбрать иначе, то плечи сил будут иными.
Плечи сил F1, F2 и силы тяжести равны нулю, так как точка О лежит с ними на одной прямой (или на самой силе). Плечо силы реакции опоры — это длина d1. Плечо силы трения — это длина d2.
Момент силы
Это векторная величина, определяется по формуле
Направление вектора момента силы определяется следующим образом. Представляем в какую сторону сила пытается повернуть (тащить) тело относительно точки О, если тело с точкой О закреплены осью. Если по часовой стрелки, то вектор имеет знак «+», если против часовой, тогда знак «-«.
Момент силы реакции опоры отрицательный, так как сила реакции опоры «поворачивает» тело против часовой стрелки
Момент силы тяжести положительный, так как сила тяжести «поворачивает» тело по часовой стрелки
Если точка О выбрана на теле
Момент силы реакции опоры и силы трения положительные, так как силы «поворачивают» тело по часовой стрелки
Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:

Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
Определение реакций для двухопорной балки
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
Как видишь, реакции опор найдены правильно.
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:


Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:


Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:
Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:
Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.
Реакции опор для плоской рамы
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции RA:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!
Плечо силы — кратчайшее расстояние между линией действия силы и связанной с ней точкой (полюсом или осью вращения) при создании силой момента.
Определяется длинной нормали (перпендикуляра) к линии усилия проведенной из рассматриваемой точки.
Обозначается: L, l или h. Измеряется в метрах [м].
Плечо силы – один из двух множителей определяющих момент силы.
Наш короткий видеоурок про момент и плечо силы с примерами:
Другие видео
О плече силы можно говорить только тогда, когда есть прямая связь между силой и точкой относительно которой возникает момент.
Порядок нахождения плеча силы
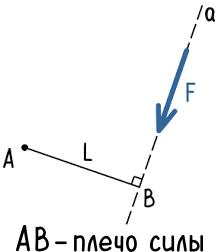
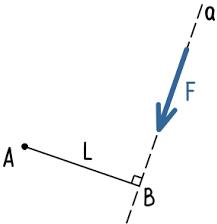
Рассмотрим порядок нахождения плеча силы F относительно точки A.
Для этого покажем прямую a, по направлению действия силы F
Из точки A опустим перпендикуляр к прямой a.
Длина этого перпендикуляра является плечом силы.
Примеры определения плеча силы
- Сила расположена перпендикулярно оси стержня и известно расстояние между точками A и B.
Плечо силы относительно точки A равно длине отрезка AB. - Сила расположена под определенным углом к оси стержня
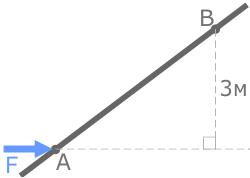
Плечо силы относительно точки B составляет AB×cos30° - Известно расстояние от точки до линии действия силы
Плечо силы относительно точки B равно 3м.
Примеры решения задач >
Момент силы >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Плечо силы — кратчайшее расстояние между линией действия силы и связанной с ней точкой (полюсом или осью вращения) при создании силой момента.
Определяется длинной нормали (перпендикуляра) к линии усилия проведенной из рассматриваемой точки.
Обозначается: L, l или h. Измеряется в метрах [м].
Плечо силы – один из двух множителей определяющих момент силы.
Порядок нахождения плеча силы
Рассмотрим порядок нахождения плеча силы F относительно точки A.
Для этого покажем прямую a, по направлению действия силы F
Из точки A опустим перпендикуляр к прямой a.
Длина этого перпендикуляра является плечом силы.
Примеры определения плеча силы
- Сила расположена перпендикулярно оси стержня и известно расстояние между точками A и B.
Плечо силы относительно точки A равно длине отрезка AB. - Сила расположена под определенным углом к оси стержня
Плечо силы относительно точки B составляет AB×cos30° - Известно расстояние от точки до линии действия силы
Плечо силы относительно точки B равно 3м.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Момент силы
О чем эта статья:
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
- Сила — это физическая векторная величина, является мерой действия тела на другое тело.
Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Плечо силы
Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.
Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.
Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.
То есть перпендикуляр, проведенный от точки опоры до линии, вдоль которой действует сила — это плечо силы.
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Рычаг
В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.
Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.
Хорошо, теперь давайте найдём плечо этой конструкции. Возьмём правую часть качелей. На качели действует сила тяжести правого качающегося, проведём перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.
Правило равновесия рычага
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.
F1, F2 — силы, действующие на рычаг
Момент силы
При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.
Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.
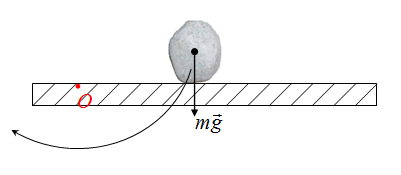
Момент силы — это произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.
Момент силы
M = Fl
M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]
Для примера представьте, что вы забыли, как открывать двери. Стоите перед дверью и раздумываете, как легче это сделать.
Для начала приложим силу к краю двери — туда, где самый длинный рычаг. Открылась!
А что если толкнуть дверь ближе к креплению — там, где плечо намного короче? Для этого придётся приложить силу большего значения.
Вывод: чтобы повернуть дверь, нужен крутящий момент определенного значения. Чем больше плечо силы, тем меньше значение силы, которую нужно приложить — и наоборот. Поэтому нам легче толкать дверь там, где плечо силы больше.
Похожая история с гаечным ключом. Чтобы закрутить гайку, нужно взяться за ручку подальше от гайки. За счет увеличения плеча мы уменьшаем значение силы, которую нужно приложить.
Расчёт момента силы
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.
Расстояние между точками A и B — 3 метра.
Момент силы относительно точки A:
Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.
Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!
Момент силы относительно точки B:
Если известно самое короткое расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).
Момент силы относительно точки B:
Правило моментов
Вернемся к нашим баранам качелям. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.
Это условие выполняется относительно любой точки.
Правило моментов
M1 + M2 +. + Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]
M’1 + M’2 +. + M’n — сумма моментов сил, поворачивающих рычаг против часовой стрелке [Н*м]
Давайте рассмотрим этот закон на примере задач.
Задача 1
К левому концу невесомого стержня прикреплен груз массой 3 кг.
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?
Решение:
Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом: — он вращает по часовой.
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг
Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг
Задача 2
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
Решение:
По правилу рычага:
где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:
Ответ: расстояние ОА равно 30 см
Задача 3
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
Решение:
По правилу рычага
Ответ: Масса груза равна 0,3 кг
Задача 4 — a.k.a самая сложная задачка
Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?
Решение:
Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Уточним, что 0,8 м — это расстояние от центра тяжести груза до опоры, т. е. перпендикуляр до оси вращения. Приравнивая моменты, получаем выражение для модуля силы тяжести
Ответ: модуль силы тяжести, действующей на груз равен 750 Н
I. Механика
Тестирование онлайн
Плечо силы
Плечо силы — это длина перпендикуляра из некоторой вымышленной точки О к силе. Вымышленный центр, точку О, будем выбирать произвольно, моменты каждой силы определяем относительно этой точки. Нельзя для определения моментов одних сил выбрать одну точку О, а для нахождения моментов других сил выбрать ее в другом месте!
На камень действуют сила тяжести, сила трения, сила реакции опоры, две дополнительные внешние силы F1 и F2
Выбираем точку О в произвольном месте, больше ее местоположение не изменяем. Тогда плечо силы тяжести — это длина перпендикуляра (отрезок d) на рисунке
Плечо силы реакции опоры определяется аналогично
Если перпендикуляр нет возможности построить, то вектор силы продлевается в необходимом направлении, после чего строим перпендикуляр к этой линии. Плечо силы F2
Осталась сила трения! Если точка О и сила лежат на одной линии, то плечо этой силы равно нулю. Плечо силы трения равно нулю.
При решении задач выгодно точку О выбирать в точке пересечения нескольких сил. Тогда плечи всех этих сил будут нулевыми. Например, если точку О в предыдущем примере выбрать иначе, то плечи сил будут иными.
Плечи сил F1, F2 и силы тяжести равны нулю, так как точка О лежит с ними на одной прямой (или на самой силе). Плечо силы реакции опоры — это длина d1. Плечо силы трения — это длина d2.
Момент силы
Это векторная величина, определяется по формуле
Направление вектора момента силы определяется следующим образом. Представляем в какую сторону сила пытается повернуть (тащить) тело относительно точки О, если тело с точкой О закреплены осью. Если по часовой стрелки, то вектор имеет знак «+», если против часовой, тогда знак «-«.
Момент силы реакции опоры отрицательный, так как сила реакции опоры «поворачивает» тело против часовой стрелки
Момент силы тяжести положительный, так как сила тяжести «поворачивает» тело по часовой стрелки
Если точка О выбрана на теле
Момент силы реакции опоры и силы трения положительные, так как силы «поворачивают» тело по часовой стрелке.