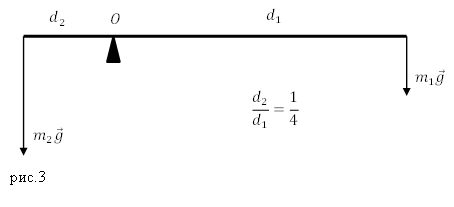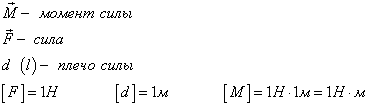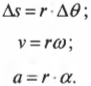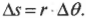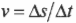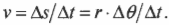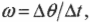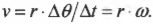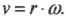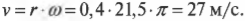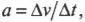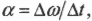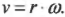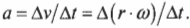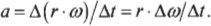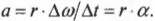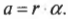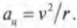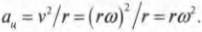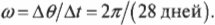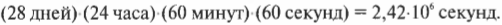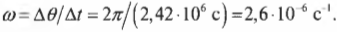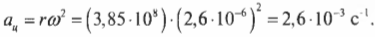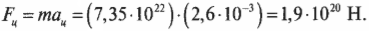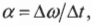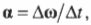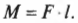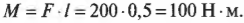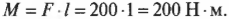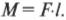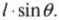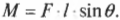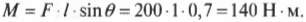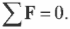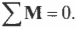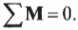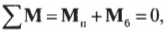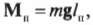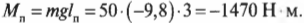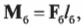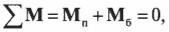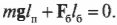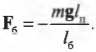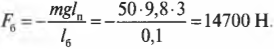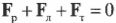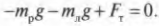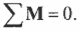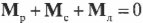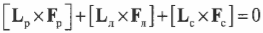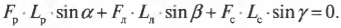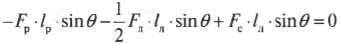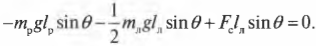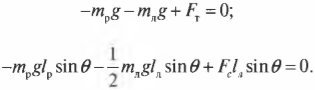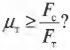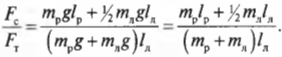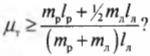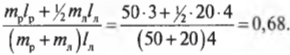I. Механика
Тестирование онлайн
Плечо силы
Плечо силы — это длина перпендикуляра из некоторой вымышленной точки О к силе. Вымышленный центр, точку О, будем выбирать произвольно, моменты каждой силы определяем относительно этой точки. Нельзя для определения моментов одних сил выбрать одну точку О, а для нахождения моментов других сил выбрать ее в другом месте!
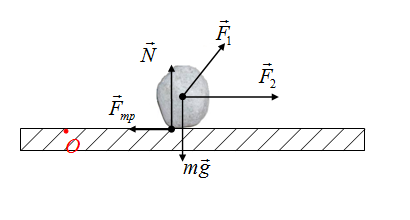
На камень действуют сила тяжести, сила трения, сила реакции опоры, две дополнительные внешние силы F1 и F2
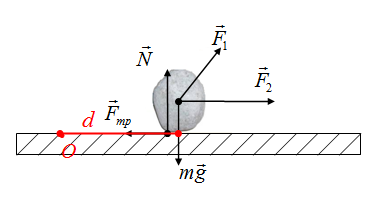
Выбираем точку О в произвольном месте, больше ее местоположение не изменяем. Тогда плечо силы тяжести — это длина перпендикуляра (отрезок d) на рисунке
Плечо силы реакции опоры определяется аналогично
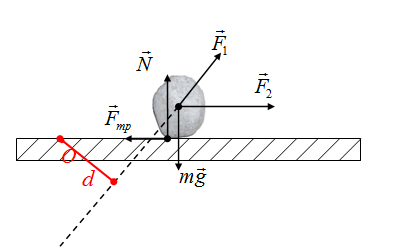
Если перпендикуляр нет возможности построить, то вектор силы продлевается в необходимом направлении, после чего строим перпендикуляр к этой линии. Плечо силы F2
Осталась сила трения! Если точка О и сила лежат на одной линии, то плечо этой силы равно нулю. Плечо силы трения равно нулю.
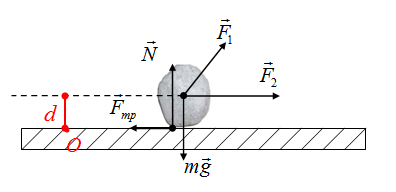
При решении задач выгодно точку О выбирать в точке пересечения нескольких сил. Тогда плечи всех этих сил будут нулевыми. Например, если точку О в предыдущем примере выбрать иначе, то плечи сил будут иными.
Плечи сил F1, F2 и силы тяжести равны нулю, так как точка О лежит с ними на одной прямой (или на самой силе). Плечо силы реакции опоры — это длина d1. Плечо силы трения — это длина d2.
Момент силы
Это векторная величина, определяется по формуле
Направление вектора момента силы определяется следующим образом. Представляем в какую сторону сила пытается повернуть (тащить) тело относительно точки О, если тело с точкой О закреплены осью. Если по часовой стрелки, то вектор имеет знак «+», если против часовой, тогда знак «-«.
Момент силы реакции опоры отрицательный, так как сила реакции опоры «поворачивает» тело против часовой стрелки
Момент силы тяжести положительный, так как сила тяжести «поворачивает» тело по часовой стрелки
Если точка О выбрана на теле
Момент силы реакции опоры и силы трения положительные, так как силы «поворачивают» тело по часовой стрелки
Определение и свойства момента силы
Момент силы относительно точки
Определение момента
Если выбрать прямоугольную систему координат Oxyz с центром в точке O , то момент силы будет иметь следующие компоненты:
(1.1) ;
(1.2) ;
(1.3) .
Здесь – координаты точки A в выбранной системе координат:
.
Компоненты представляют собой значения момента силы относительно осей , соответственно.
Определение плеча силы
Свойства
Если точку приложения силы переместить вдоль линии ее действия, то момент, при таком перемещении, не изменится.
Доказательство ⇓
Абсолютная величина момента силы относительно некоторой точки равна произведению абсолютного значения силы на плечо этой силы относительно выбранной точки.
Доказательство ⇓
Момент относительно точки O , от силы, линия действия которой проходит через эту точку, равен нулю.
Доказательство ⇓
Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:
.
Доказательство ⇓
Тоже самое относится и к силам, чьи линии продолжения пересекаются в одной точке. При этом в качестве точки приложения суммы сил берется точка пересечения линий их действия.
Если векторная сумма сил равна нулю:
,
то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
.
Доказательство ⇓
Момент силы является псевдовектором или, что то же самое, аксиальным вектором.
Это свойство следует из свойства векторного произведения. Поскольку векторы и являются истинными (или полярными) векторами, то их векторное произведение является псевдовектором. Это означает то, что мы можем определить только абсолютное значение и ось, вдоль которой направлено векторное произведение. Само же направление по этой оси мы задаем произвольным образом, используя правило правого винта. То есть мы мысленно откладываем векторы и из одного центра. Затем поворачиваем ручку из положения в положение . В результате правый винт смещается в направлении, перпендикулярном плоскости, в которой расположены векторы. Это направление мы и берем за направление векторного произведения.
Но если бы мы определили направление по правилу левого винта, то векторное произведение было бы направлено в противоположную сторону. При этом никакого противоречия не возникает. То есть фактически, аксиальные векторы могут иметь два взаимно противоположных направления. Чтобы не усложнять математические формулы, мы выбираем одно из них, применяя правило правого винта. По этой причине, псевдовекторы нельзя геометрически складывать с истинными векторами. Но их можно перемножать, используя скалярное или векторное произведение.
Момент силы относительно оси
Определение
Часто встречаются случаи, когда нам не нужно знать все компоненты момента силы относительно выбранной точки, а нужно знать только момент силы относительно выбранной оси.
Момент силы относительно оси – это проекция вектора момента силы относительно произвольной точки, принадлежащей этой оси, на направление оси.
Пусть – единичный вектор, направленный вдоль оси. И пусть O – произвольная точка, принадлежащая ей. Тогда момент силы относительно оси является скалярным произведением:
.
Такое определение возможно, поскольку для любых двух точек O и O′ , принадлежащих оси, проекции моментов относительно этих точек на ось равны. Покажем это.
Воспользуемся векторным уравнением :
;
.
Умножим это уравнение скалярно на единичный вектор , направленный вдоль оси:
.
Поскольку вектор параллелен оси, то . Отсюда
.
То есть проекции моментов на ось, относительно точек O и O′ , принадлежащих этой оси, равны.
Свойства
Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
Доказательство ⇓
Момент относительно оси от силы, параллельной этой оси равен нулю.
Доказательство ⇓
Доказательство свойств
Перемещение точки приложения силы вдоль линии ее действия
Все свойства ⇑ Если точку приложения силы переместить вдоль линии действия силы, то момент, при таком перемещении, не изменится.
Пусть сила приложена в точке A . Через точку A проведем прямую, параллельную вектору силы. Эта прямая является линией ее действия. Переместим точку A приложения силы в точку A′ , принадлежащую линии действия. Тогда
.
Вектор проведен через две точки линии действия. Поэтому его направление совпадает или противоположно направлению вектора силы . Тогда , где λ – параметр; . , если точка A′ смещена относительно A в направлении вектора . В противном случае .
Таким образом, вектор, проведенный из O в A′ , имеет вид:
.
Найдем момент силы, приложенной в точке A′ , применяя свойства векторного произведения:
.
Мы видим, что момент не изменился:
.
Абсолютная величина момента силы
Все свойства ⇑ Абсолютная величина момента силы относительно некоторой точки равна произведению абсолютного значения силы на плечо этой силы относительно выбранной точки.
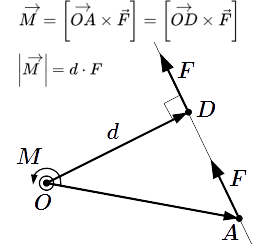
Абсолютное значение момента M относительно точки O равно произведению силы F на ее плечо d = |OD| .
Пусть мы имеем силу , приложенную в точке A . Рассмотрим момент этой силы относительно некоторой точки O . Заметим, что точки O , A и вектор лежат в одной плоскости. Изобразим ее на рисунке. Через точку A , в направлении вектора проводим прямую AB . Эта прямая называется линией действия силы . Через точку O опустим перпендикуляр OD к линии действия. И пусть D является точкой пересечения линии действия и перпендикуляра. Тогда – плечо силы относительно центра O . Обозначим его буквой . Воспользуемся предыдущим свойством ⇑, согласно которому точку приложения силы можно перемещать вдоль ее линии действия. Переместим ее в точку D . Момент силы:
.
Поскольку векторы и перпендикулярны, то по свойству векторного произведения, абсолютное значение момента:
,
где – абсолютное значение силы.
Заметим, что вектор момента перпендикулярен плоскости рисунка. Его направление определяется по правилу правого винта. Если мы будем вращать винт, проходящий через точку O перпендикулярно плоскости рисунка, в направлении силы F , то он будет перемещаться на нас. Поэтому вектор момента перпендикулярен плоскости рисунка и направлен на нас.
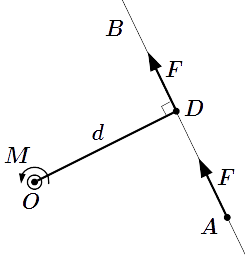
Момент относительно точки от силы, проходящей через эту точку
Все свойства ⇑ Момент относительно точки O , от силы, линия действия которой проходит через эту точку, равен нулю.
Пусть линия действия силы проходит через точку O . Тогда плечо этой силы относительно O равно нулю: . Согласно предыдущему свойству ⇑, абсолютное значение момента силы относительно выбранной точки равно нулю:
.
Момент суммы сил, приложенных в одной точке
Все свойства ⇑ Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:
.
Пусть силы приложены в одной точке A . Пусть – векторная сумма этих сил. Находим момент относительно некоторой точки O от векторной суммы , приложенной в точке A . Для этого применяем свойства векторного произведения:
.
Момент системы сил, векторная сумма которых равна нулю
Все свойства ⇑ Если векторная сумма сил равна нулю:
,
то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
.
Пусть силы приложены в точках , соответственно. И пусть точки O и C обозначают два центра, относительно которых мы будем вычислять моменты. Тогда имеют место следующие векторные уравнения:
.
Используем их при вычислении суммы моментов относительно точки O :
.
Здесь мы воспользовались тем, что по условию,
.
Момент относительно оси от силы, проходящей через эту ось
Все свойства ⇑ Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
В определении ⇑ указано, что момент силы относительно оси – это проекция вектора момента силы относительно произвольной точки, принадлежащей этой оси, на направление оси. В качестве такой точки возьмем точку пересечения линии действия силы с осью. Но, согласно доказанному выше ⇑, момент относительно этой точки равен нулю. Поэтому равна нулю и его проекция на эту ось.
Момент относительно оси от силы, параллельной этой оси
Все свойства ⇑ Момент относительно оси от силы, параллельной этой оси равен нулю.
Пусть O – произвольная точка на оси. Рассмотрим момент силы относительно этой точки. Согласно определению:
.
Согласно свойству векторного произведения, вектор момента перпендикулярен вектору силы . Поскольку вектор силы параллелен оси, то вектор момента ей перпендикулярен. Поэтому проекция момента относительно точки O на ось равна нулю.
Автор: Олег Одинцов . Опубликовано: 20-09-2019
Момент силы
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
- Сила — это физическая векторная величина, является мерой действия тела на другое тело.
Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Плечо силы
Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.
Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.
Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.
То есть перпендикуляр, проведенный от точки опоры до линии, вдоль которой действует сила —это плечо силы.
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Рычаг
В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.
Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.
Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.
Момент силы
При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.
Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.
Момент силы — это произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.
Момент силы
M = Fl
M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]
Вернемся к примеру с дверями. Вот мы приложили силу к краю двери — туда, где самый длинный рычаг. Получаем некоторое значение момента силы.
Теперь ту же силу приложим ближе к креплению двери, там, где плечо намного короче. По формуле получим момент меньшей величины.
На себе мы это ощущаем таким образом: нам легче толкать дверь там, где момент больше. То есть, чем больше момент, тем легче идет вращение.
То же самое можно сказать про гаечный ключ. Чтобы закрутить гайку, нужно взяться за ручку дальше гайки.
В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения плеча.
Расчет момента силы
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.
Расстояние между точками A и B — 3 метра.
Момент силы относительно точки A:
Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.
Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!
Момент силы относительно точки B:
Если известно самое короткое расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).
Момент силы относительно точки B:
Правило моментов
Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.
Это условие выполняется относительно любой точки.
Правило моментов
M1 + M2 +. + Mn = M’1 + M’2 +. + M’n
M1 + M2 +. + Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]
Давайте рассмотрим этот закон на примере задач.
Задача 1
К левому концу невесомого стержня прикреплен груз массой 3 кг.
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?
Решение:
Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг
Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг
Задача 2
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
Решение:
По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:
Ответ: расстояние ОА равно 30 см
Задача 3
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
Решение:
По правилу рычага m1g*l1=m2g*l2
Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг
Ответ: Масса груза равна 0,3 кг
Задача 4
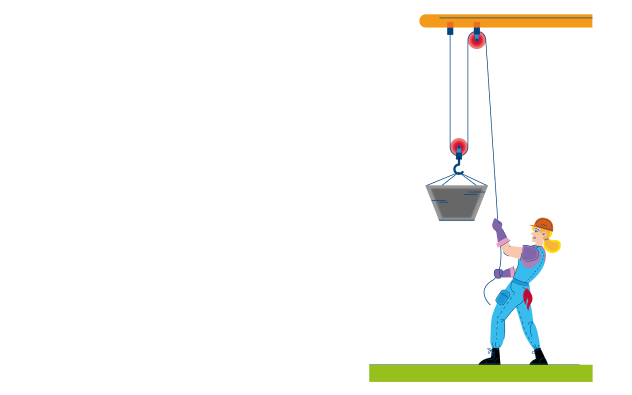
На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?
Решение:
Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.
Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н
Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно
Ответ: натяжение провода равно 400 Н
Задача 5 — a.k.a самая сложная задачка
Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?
Решение:
Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести
Ответ: модуль силы тяжести, действующей на груз равен 750 Н
http://1cov-edu.ru/mehanika/statika/moment-sily-opredelenie-i-svojstva/
http://skysmart.ru/articles/physics/moment-sily
Рассмотрим несколько задач на тему «вращательный момент» с пояснениями. Будем осуществлять расчет перпендикулярных частей сил и плеч сил в случаях, когда углы между силой и рычагом отличаются от прямого.
Это вторая часть статьи о моменте силы. Первая часть находится тут (откроется в новой вкладке).
Угол между силой и рычагом отличается от прямого
Рассмотрим рисунок 1. На рисунке 1а сила приложена к рукоятке ключа под прямым углом. На рисунках 1б и 1в углы между силой и рукояткой (рычагом) отличаются от прямого.
Рис. 1. Несколько способов приложения силы к рычагу под различными углами
Длина рычага является расстоянием между точкой приложения силы и осью вращения. Когда угол отличается от прямого, для вычисления момента силы нужно раскладывать на проекции либо силу, либо длину рычага (рукоятки).
Раскладываем силу
Разложим приложенную силу ( F ) на части. Одна часть будет располагаться перпендикулярно рукоятке, а другая – параллельно (см. рис. 2).
Рис. 2. Способ разложения силы, приложенной к рычагу под тупым (а) и острым (б) углами
Рукоятку вращает только перпендикулярная часть силы. На рисунке 2 она обозначена, как ( F_{1} ).
Параллельная рукоятке часть обозначена ( F_{2} ). Она не вращает рукоятку, а сдвигает ключ либо от гайки (рис. 2а), либо в сторону гайки (рис 2б).
Рукоятка ключа – это плечо для перпендикулярной части силы.
Момент силы для рисунка 2 считаем по формуле:
[ M = F_{1} cdot d ]
Наиболее выгодно прикладывать силу перпендикулярно рукоятке (см. рис 1а). В этом случае вращательный момент силы будет наибольшим.
В остальных случаях вращать рукоятку будет не вся сила целиком, а только лишь ее перпендикулярная часть.
Помним! Между силой и ее плечом угол прямой.
Задача 1
Угол между приложенной силой и рукояткой ключа равен 30 градусам. Определить часть вектора силы, вращающего гаечный ключ. С помощью этой части вектора силы рассчитать вращательный момент. Сила равна 20 Н. Длина рукоятки 20 см.
Рисунок.
Рис. 3. Раскладываем на проекции силу, приложенную к рычагу под острым углом
Решение:
- Проведем перпендикулярную ( F_{1} ) часть и параллельную рычагу ( F_{2} ) часть силы (рис. 3).
Примечание:
Чтобы разложить вектор силы на части, нужно нарисовать прямоугольник. Так, чтобы вектор, который мы раскладываем, оказался диагональю прямоугольника. Две стороны этого прямоугольника будут параллельны рукоятке, а другие две – перпендикулярны ей.
Тогда стороны прямоугольника обозначат проекции – перпендикулярную и продольную (параллельную).
- Вычислим перпендикулярную ( F_{1} ) часть силы:
[ F_{1} = F cdot sin(alpha)]
( sin(30^{o})=0,5)
( F_{1} = 20 cdot 0,5)
( F_{1} = 10 left(Hright))
- Рассчитаем теперь вращательный момент M этой силы:
[ M = F_{1} cdot d ]
( M = 10 cdot 0,2 )
( M = 2 left( H cdot text{м} right) )
Ответ: Вращательный момент равен ( 2 left( H cdot text{м} right) )
Раскладываем расстояние
Для подсчета вращательного момента, на проекции можно раскладывать не только силу.
На части можно разложить длину рукоятки, так, чтобы одна часть оказалась продольной силе, а другая – параллельной (рис. 4).
После выбираем часть длины, перпендикулярную силе. Эта сторона является плечом силы.
Рис. 4. Раскладываем на проекции длину рычага для приложенных под тупым (а) или острым (б) углом сил
На рисунке 4а перпендикулярно силе располагается ( d_{1} ), для этого случая момент силы считаем так:
[ M = Fcdot d_{1} ]
Из рисунка 4б выбираем перпендикулярную силе величину ( d_{2} ). Момент силы вычисляем, пользуясь формулой:
[ M = Fcdot d_{2} ]
Задача 2
Угол между приложенной силой и рукояткой ключа равен 30 градусам. Определить плечо вектора приложенной силы. С помощью этого плеча рассчитать вращательный момент. Сила равна 20 Н. Длина рукоятки 20 см.
Рис. 5. Для приложенной под острым углом силы раскладываем на проекции длину рычага
Решение:
- Проведем параллельную ( d_{1} ) и перпендикулярную силе ( d_{2} ) часть рычага (рис. 5).
Примечание:
Снова рисуем прямоугольник. Но теперь не сила, а рукоятка должна оказаться диагональю прямоугольника. Две стороны этого прямоугольника будут параллельны силе, а другие две – перпендикулярны ей.
В прямоугольнике выбираем сторону, перпендикулярную силе. Эта сторона является плечом силы.
О формулах разложения векторов на проекции подробно написано тут (откроется в новой вкладке).
- Вычислим перпендикулярную силе F часть длины ( d_{2} ) рычага – плечо силы F:
[ d_{2} = d cdot sin(alpha)]
( sin(30^{o})=0,5)
( d_{2} = 0,2 cdot 0,5)
( d_{2} = 0,1 left( text{м} right))
- Рассчитаем теперь с помощью найденного плеча ( d_{2} ) силы F вращательный момент M:
[ M = F cdot d_{2} ]
( M = 20 cdot 0,1 )
( M = 2 left( H cdot text{м} right) )
Ответ: Вращательный момент равен ( 2 left( H cdot text{м} right) )
Расчет момента силы с помощью формулы, содержащей угол между силой и рычагом
Вращательный момент можно рассчитать без прямого указания плеча силы, зная угол между силой и рычагом. Подробнее в первой части статьи (откроется в новом окне)
Задача 3
Угол между приложенной силой и рукояткой ключа равен 30 градусам. Не рассчитывая плеча силы найти вращательный момент. Сила равна 20 Н. Длина рукоятки 20 см.
Рис. 6. Рассчитаем момент приложенной под острым углом силы без разложения на проекции
Решение:
- Воспользуемся формулой для вычисления вращательного момента:
[ M = F cdot d cdot sin(alpha)]
( sin(30^{o})=0,5)
( M = 20 cdot 0,2 cdot 0,5)
( M = 2 left( H cdot text{м} right) )
Ответ: Вращательный момент равен ( 2 left( H cdot text{м} right) )
Как видно из задач 1 — 3, все три способа вычисления вращательного момента дают аналогичные результаты.
Формула плеча силы в физике
Формула плеча силы
Определение и формула плеча силы
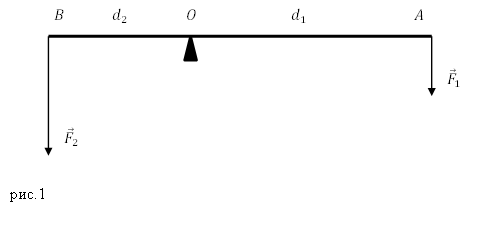
Рассмотрим рычаг с осью вращения находящийся в точке О. (рис.1). Силы ${overline{F}}_1$ и ${overline{F}}_2$, действующие на рычаг направлены в одну сторону.
Минимальное расстояние между точкой опоры (точка О) и прямой, вдоль которой действует на рычаг сила, называют плечом силы.
Для нахождения плеча силы следует из точки опоры опустить перпендикуляр к линии действия силы. Длинна данного перпендикуляра и станет плечом рассматриваемой силы. Так, на рис.1 расстояние $left|OAright|=d_1$- плечо силы $F_1$; $left|OAright|=d_2$- плечо силы $F_2$.
Рычаг находится в состоянии равновесия, если выполняется равенство:
[frac{F_1}{F_2}=frac{d_2}{d_1}left(1right).]
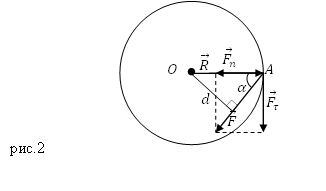
Предположим, что материальная точка движется по окружности (рис.2) под действием силы $overline{F}$ (сила действует в плоскости движения точки). В таком случае угловое ускорение ($varepsilon $) точки определяется тангенциальной составляющей ($F_{tau }$) силы $overline{F}$:
[mRvarepsilon =F_{tau }left(2right),]
где $m$ — масса материальной точки; $R$ — радиус траектории движения точки; $F_{tau }$ — проекция силы на направление скорости движения точки.
Если угол $alpha $ — это угол между вектором силы $overline{F}$ и радиус — вектором $overline{R}$, определяющим положение рассматриваемой материальной точки (Этот радиус- вектор проведен из точки О в точку А на рис.2), тогда:
[F_{tau }=F{sin alpha left(3right). }]
Расстояние $d$ между центром O и линией действия силы $overline{F}$ называют плечом силы. Из рис.2 следует, что:
[d=R{sin alpha left(4right). }]
Если на точку будет действовать сила ($overline{F}$), направленная по касательной к траектории ее движения, то плечо силы будет равно $d=R$, так как угол $alpha $ станет равен $frac{pi }{2}$.
Момент силы и плечо
Понятие плечо силы иногда используют, для записи величины момента силы ($overline{M}$), который равен:
[overline{M}=left[overline{r}overline{F}right]left(5right),]
где $overline{r}$ — радиус — вектор проведенный к точке продолжения силы$ overline{F}$. Модуль вектора момента силы равен:
[M=F{rsin alpha = }Fd left(6right).]
Построение плеча силы
И так, плечом силы называют длину перпендикуляра, который проводят из некоторой выбранной точки, иногда ее называют полюсом (выбираемой произвольно, но при рассмотрении одной задачи один раз). При рассмотрении задач точку О выбирают обычно на пересечении нескольких сил) к силе (рис.3 (а)). Если точка О будет лежать на одной прямой с силами или на самой силе, то плечи сил будут равны нулю.
Если перпендикуляр не получается построить, то вектор силы продлевают в нужном направлении, после этого строят перпендикуляр (рис.3 (б)).
Примеры задач с решением
Пример 1
Задание. Какова масса меньшего тела ($m_1$), если его уравновешивает тело массой $m_2={rm 2 }$кг? Тела находятся на невесомом рычаге (рис.3) отношение плеч рычага 1:4?
Решение. Основой решения задачи является правило равновесия рычага:
[frac{F_1}{F_2}=frac{d_2}{d_1}left(1.1right),]
где силы, действующие на концы рычага равны по модулю силам тяжести, которые действуют на тела, следовательно, формулу (1.1) перепишем в виде:
[frac{m_1g}{m_2g}=frac{d_2}{d_1}to frac{m_1}{m_2}=frac{d_2}{d_1}left(1.2right).]
Из выражения (1.2) получим искомую массу $m_1$:
[m_1=frac{m_2d_2}{d_1}.]
Вычислим искомую массу:
[m_1=2cdot frac{1}{4}=0,5 (кг).]
Ответ. $m_1=0,5 кг$
Пример 2
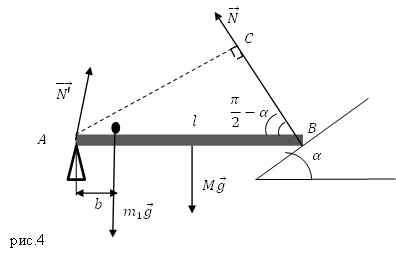
Задание. Однородный стержень длинной $l $и массой $M$ расположен горизонтально. Один конец стержня в точке А закреплён так, что может вращаться вокруг этой точки, другой конец опирается на наклонную плоскость, угол наклона которой к горизонту равен $alpha $. На стержне на расстоянии $b $от точки А лежит небольшой груз. Каковы плечи сил, действующих на стержень?
Решение. Изобразим на рис.4 силы, действующие на стержень. Это: сила тяжести: $Moverline{g}$, вес груза, расположенного на нем $overline{P}=m_1overline{g}$, сила реакции наклонной плоскости: $overline{N}$; сила реакции опоры в точке A: $overline{N}’$.
Плечи сил будем искать относительно точки A. Плечо силы $overline{N’}$ будет равно нулю, так как сила приложена к стержню в точке А:
[d_{N’}=0 left(2.1right).]
Плечо другой силы реакции опоры ($overline{N}$) равно длине перпендикуляра AC:
[d_N=l{sin (90-alpha ) }=l{cos alpha left(2.2right). }]
Плечо силы $Moverline{g}$ из рис.4 , так как сила тяжести приложена к центру масс стержня, который для однородного стержня находится на его середине:
[d_{Mg}=frac{l}{2}left(2.3right).]
Плечо силы $m_1overline{g},$ учитывая, что груз маленький и принимая его за материальную точку, равно:
[d_{m_1g}=b.]
Ответ. $d_{N’}=0;; d_N=l{sin (90-alpha ) }=l{cos alpha left(мright), }d_{Mg}=frac{l}{2}, d_{m_1g}=b$
Читать дальше: формула полезной мощности.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
I. Механика
Тестирование онлайн
Плечо силы
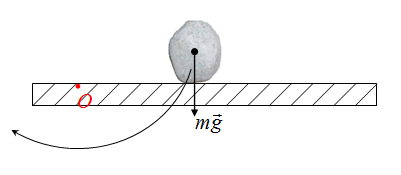
Плечо силы — это длина перпендикуляра из некоторой вымышленной точки О к силе. Вымышленный центр, точку О, будем выбирать произвольно, моменты каждой силы определяем относительно этой точки. Нельзя для определения моментов одних сил выбрать одну точку О, а для нахождения моментов других сил выбрать ее в другом месте!
На камень действуют сила тяжести, сила трения, сила реакции опоры, две дополнительные внешние силы F1 и F2
Выбираем точку О в произвольном месте, больше ее местоположение не изменяем. Тогда плечо силы тяжести — это длина перпендикуляра (отрезок d) на рисунке
Плечо силы реакции опоры определяется аналогично
Если перпендикуляр нет возможности построить, то вектор силы продлевается в необходимом направлении, после чего строим перпендикуляр к этой линии. Плечо силы F2
Плечо силы F1
Осталась сила трения! Если точка О и сила лежат на одной линии, то плечо этой силы равно нулю. Плечо силы трения равно нулю.
При решении задач выгодно точку О выбирать в точке пересечения нескольких сил. Тогда плечи всех этих сил будут нулевыми. Например, если точку О в предыдущем примере выбрать иначе, то плечи сил будут иными.
Плечи сил F1, F2 и силы тяжести равны нулю, так как точка О лежит с ними на одной прямой (или на самой силе). Плечо силы реакции опоры — это длина d1. Плечо силы трения — это длина d2.
Момент силы
Это векторная величина, определяется по формуле
Направление вектора момента силы определяется следующим образом. Представляем в какую сторону сила пытается повернуть (тащить) тело относительно точки О, если тело с точкой О закреплены осью. Если по часовой стрелки, то вектор имеет знак «+», если против часовой, тогда знак «-«.
Момент силы реакции опоры отрицательный, так как сила реакции опоры «поворачивает» тело против часовой стрелки
Момент силы тяжести положительный, так как сила тяжести «поворачивает» тело по часовой стрелки
Если точка О выбрана на теле
Момент силы реакции опоры и силы трения положительные, так как силы «поворачивают» тело по часовой стрелки
В этой главе…
- Переходим от поступательного движения к вращательному движению
- Вычисляем тангенциальную скорость и тангенциальное ускорение
- Выясняем связь между угловым ускорением и угловой скоростью
- Разбираемся с моментом силы
- Поддерживаем вращательное движение
Эта и следующая главы посвящены вращательному движению объектов самой разной природы: от космических станций до пращи. Именно такое движение стало причиной того, что наша планета имеет круглую форму. Если вам известны основные свойства прямолинейного движения и законы Ньютона (они подробно описываются в двух первых частях этой книги), то вы сможете быстро овладеть основами вращательного движения. Даже если вы позабыли некоторые сведения из прежних глав, не беда, ведь к ним всегда можно вернуться в случае необходимости. В этой главе представлены основные понятия вращательного движения: угловая скорость угловое ускорение, тангенциальное ускорение, момент силы и т.п. Однако довольно слов, приступим к делу!
Содержание
- Переходим от прямолинейного движения к вращательному
- Разбираемся с параметрами вращательного движения
- Вычисляем линейную скорость вращательного движения
- Вычисляем тангенциальное ускорение
- Вычисляем центростремительное ускорение
- Используем векторы для изучения вращательного движения
- Определяем направление угловой скорости
- Определяем направление углового ускорения
- Поднимаем грузы: момент силы
- Знакомимся с формулой момента силы
- Разбираемся с направлением приложенной силы и плечом силы
- Размышляем над тем, как создается момент силы
- Определяем направление момента силы
- Уравновешиваем моменты сил
- Простой пример: вешаем рекламный плакат
- Более сложный пример: учитываем силу трения при расчете равновесия
Переходим от прямолинейного движения к вращательному
Для такого перехода нужно изменить уравнения, которые использовались ранее для описания прямолинейного движения. В главе 7 уже упоминались некоторые эквиваленты (или аналоги) из мира прямолинейного и вращательного движения.
Вот как выглядят основные формулы прямолинейного движения, которые подробно описываются в главе 3:
- ( v=Delta{s}/Delta{t} ), где ( v ) — это скорость, ( Delta{s} ) — перемещение, a ( Delta{t} ) — время перемещения;
- ( a=Delta{v}/Delta{t} ), где ( a ) — это ускорение, ( Delta{v} ) — изменение скорости, a ( Delta{t} ) — время изменения скорости;
- ( Delta{s}=v_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 ), где ( v_0 ) — это начальная скорость, ( t_0 ) — это начальный момент времени, a ( t_1 ) — это конечный момент времени;
- ( v^2_1-v^2_0=2aDelta{s} ), где ( v_1 ) — это конечная скорость.
По аналогии можно легко вывести основные формулы вращательного движения:
- ( omega=Delta{theta}/Delta{t} ), где ( omega ) — угловая скорость, ( Delta{theta} ) — угол поворота, ( Delta{t} ) — время поворота на угол ( Delta{theta} );
- ( alpha=Delta{omega}/Delta{t} ), где ( alpha ) — угловое ускорение, ( Delta{omega} ) — изменение угловой скорости, ( Delta{t} ) — время изменения угловой скорости;
- ( theta=omega_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 ), где ( omega_0 ) — это начальная скорость;
- ( omega^2_1-w^2_0=2as ), где ( omega_1 ) — это конечная скорость.
Разбираемся с параметрами вращательного движения
В физике движение принято разделять на поступательное и вращательное. При поступательном движении любая прямая, связанная с движущимся объектом, остается параллельной самой себе. При вращательном движении все точки тела движутся по окружностям. Тангенциальным движением называется часть вращательного движения, происходящего по касательной к окружности вращения, а радиальным (или нормальным) движением — часть вращательного движения, происходящего перпендикулярно (по нормали) к касательной, т.е. вдоль радиуса окружности.
Параметры прямолинейного поступательного и вращательного движений можно связать следующими формулами:
Допустим, колеса мотоцикла вращаются с угловой скоростью ( omega ), равной 21,5( 21,5pi ) радиан в секунду. С какой скоростью едет мотоцикл? Чтобы дать ответ на этот вопрос, достаточно воспользоваться простой формулой связи линейной и угловой скорости.
Вычисляем линейную скорость вращательного движения
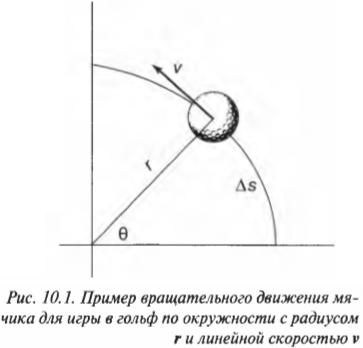
Скорость тангенциального движения материальной точки принято называть линейной скоростью вращательного движения. На рис. 10.1 приведен пример вращения мячика для игры в гольф по окружности с радиусом ( mathbf{r} ) и линейной скоростью ( mathbf{v} ). Скорость ( mathbf{v} ) является векторной величиной, т.е. обладает величиной и направлением (подробнее о векторах рассказывается в главе 4), перпендикулярным радиус-вектору ( mathbf{r} ).
Угловая скорость связана с линейной скоростью соотношением ( v=romega ), которое легко интуитивно понять. При одинаковой угловой скорости, чем дальше материальная точка от центра окружности вращения, тем больше ее линейная скорость.
Попробуем получить уже упомянутую выше формулу связи линейной и угловой скорости ( v=romega ). Длина окружности ( L ) радиуса ( r ) выражается известной формулой ( L=2pi r ), а полный угол, который охватывает окружность, равен ( 2pi ) радиан. Соответственно, длина дуги окружности длиной ( Delta s ), охватывающая угол ( Deltatheta ), равна:
Из формулы прямолинейного движения
путем подстановки выражения для ( Delta s ) получим:
Поскольку:
где ( omega ) — угловая скорость, ( Delta{theta} )— угол поворота, ( Delta{t} ) — время поворота на угол ( Delta{theta} ), то:
Теперь можно легко и просто дать ответ на вопрос, поставленный в конце предыдущего раздела, т.е. определить скорость мотоцикла по угловой скорости вращения его колес. Итак, колеса мотоцикла вращаются с угловой скоростью ( omega ), равной 21,5( pi ) радиан в секунду. Пусть радиус колеса ( r ) равен 40 см, тогда достаточно использовать следующую формулу:
Подставляя в нее значения, получим:
Итак, скорость мотоцикла равна 27 м/с или 97 км/ч.
Вычисляем тангенциальное ускорение
Тангенциальным ускорением называется скорость изменения величины линейной скорости вращательного движения. Эта характеристика вращательного движения очень похожа на линейное ускорение прямолинейного движения (см. главу 3). Например, точки на колесе мотоцикла в момент старта имеют нулевую линейную скорость, а спустя некоторое время после разгона ускоряются до некоторой ненулевой линейной скорости. Как определить это тангенциальное ускорение точки колеса? Переформулируем вопрос: как связать линейное ускорение
где ( a ) — это ускорение, ( Delta v ) — изменение скорости, a ( Delta t ) — время изменения скорости, с угловым ускорением
где ( Deltaomega ) — изменение угловой скорости, ( Delta t ) — время изменения угловой скорости?
Как мы уже знаем, линейная и угловая скорости связаны равенством
Подставим это выражение в предыдущую формулу линейного ускорения:
Поскольку радиус остается постоянным, то его можно вынести за скобки:
Поскольку угловое ускорение ( alpha=Deltaomega/Delta t ), то:
Итак, получаем следующую формулу связи между линейным и угловым ускорением:
Иначе говоря, тангенциальное ускорение равно произведению радиуса на угловое ускорение.
Вычисляем центростремительное ускорение
Центростремительнным ускорением называется ускорение, необходимое для удержания объекта на круговой орбите вращательного движения. Как связаны угловая скорость и центростремительное ускорение? Формула для центростремительного ускорения уже приводилась ранее (см. главу 7):
Теперь, используя известную формулу связи линейной и угловой скорости ( v=romega ), получим:
По этой формуле можно определить величину центростремительного ускорения по известной угловой скорости и радиусу. Например, для вычисления центростремительного ускорения Луны, вращающейся вокруг Земли, удобно использовать именно эту формулу.
Луна делает полный оборот вокруг Земли за 28 дней, т.е. за 28 дней Луна проходит ( 2pi ) радиан. Отсюда получаем угловую скорость Луны:
Чтобы получить значение угловой скорости в привычных единицах, следует преобразовать дни в секунды:
После подстановки этого значения в предыдущую формулу получим:
Средний радиус орбиты Луны равен 3,85·108 м. Подставляя эти значения угловой скорости и радиуса в формулу центростремительного ускорения, получим:
Зная это ускорение и массу Луны, которая равна 7,35·1022 кг, можно определить центростремительную силу, необходимую для удержания Луны на ее орбите:
Используем векторы для изучения вращательного движения
В предыдущих разделах этой главы угловая скорость и угловое ускорение рассматривались как скаляры, т.е. как параметры, характеризующиеся только величиной. Однако эти параметры вращательного движения, на самом деле, являются векторами, т.е. они обладают величиной и направлением (см. главу 4). В этом разделе рассматривается величина и направление некоторых параметров вращательного движения.
Определяем направление угловой скорости
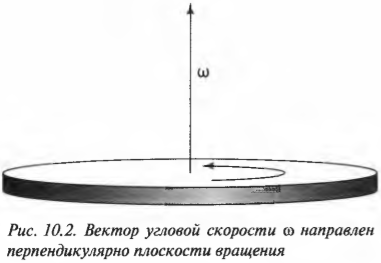
Как нам уже известно, вращающееся колесо мотоцикла имеет не только угловую скорость, но и угловое ускорение. Что можно сказать о направлении вектора угловой скорости? Оно не совпадает с направлением линейной тангенциальной скорости, а… перпендикулярно плоскости колеса!
Эта новость всегда приводит к некоторому замешательству среди новичков: угловая скорость ( omega ), оказывается, направлена вдоль оси вращающегося колеса (рис. 10.2). Во вращающемся колесе единственной неподвижной точкой является его центр. Поэтому начало вектора угловой скорости принято располагать в центре окружности вращения.
Для определения направления вектора угловой скорости ( omega ) часто используют правило правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление тангенциальной скорости, то вытянутый большой палец укажет направление вектора угловой скорости ( omega ).
Теперь угловую скорость можно использовать так же, как и остальные векторные характеристики движения. Направление вектора угловой скорости можно найти по правилу правой руки, а величину — по приведенной ранее формуле. То, что вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, часто вызывает некоторые трудности у начинающих, но к этому можно быстро привыкнуть.
Определяем направление углового ускорения
Если вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, то куда направлен вектор углового ускорения в случае замедления или ускорения вращения объекта? Как известно (см. предыдущие разделы), угловое ускорение определяется формулой:
где ( alpha ) — угловое ускорение, ( Deltaomega ) — изменение угловой скорости, ( Delta t )— время изменения угловой скорости.
В векторной форме оно имеет следующий вид:
где ( mathbf{alpha} ) — вектор углового ускорения, а ( Deltamathbf{omega} ) — изменение вектора угловой скорости. Отсюда ясно, что направление вектора углового ускорения совпадает с направлением изменения вектора угловой скорости.
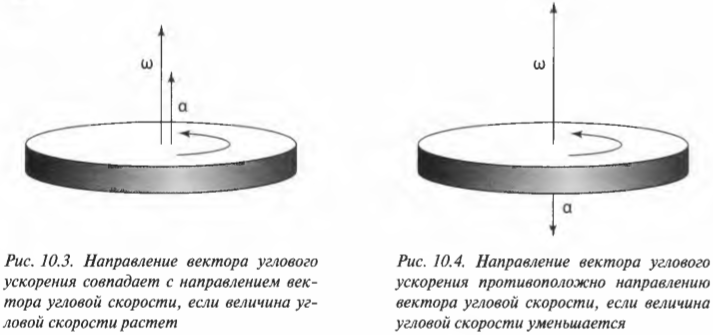
Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление вектора углового ускорения совпадает с направлением вектора угловой скорости, как показано на рис. 10.3.
А если величина угловой скорости падает, то направление вектора углового ускорения противоположно направлению вектора угловой скорости, как показано на рис. 10.4.
Поднимаем грузы: момент силы
В физике большое значение имеет не только время, но и место приложения силы. Всем когда-либо приходилось пользоваться рычагом для перемещения тяжелых грузов. Чем длиннее рычаг, тем легче сдвинуть груз. На языке физики применение силы с помощью рычага характеризуется понятием момент силы.
Приложение момента силы неразрывно связано с вращательным движением объектов. Если приложить силу к краю карусели, то карусель начнет вращательное движение. Чем дальше точка приложения силы, тем легче раскрутить карусель до заданной угловой скорости (параметры вращательного движения описываются в главе 1 1 ).
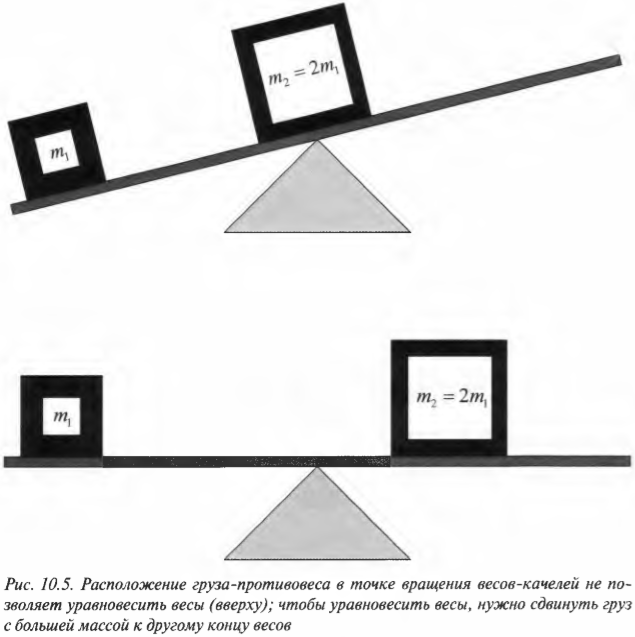
В верхней части рис. 10.5 показаны весы-качели с грузом массы ( m_1 ) на одном конце и грузом большей массы ( m_2=2m_1 ) посередине. Чтобы уравновесить весы-качели, нужно сместить груз с большей массой ( m_2 ) к другому концу весов, как показано в нижней части рис. 10.5. Как известно из опыта, размещение груза в точке вращения весов не приводит к уравновешиванию весов. Чтобы уравновесить весы, нужно сдвинуть груз с большей массой ( m_2=2m_1 ) к другому концу весов на расстояние вдвое меньшее, чем расстояние от точки вращения до второго груза с массой ( m_1 ).
Знакомимся с формулой момента силы
Для уравновешивания весов важно не только, какая сила используется, но и где она прикладывается. Расстояние от точки приложения силы до точки вращения называется плечом силы.
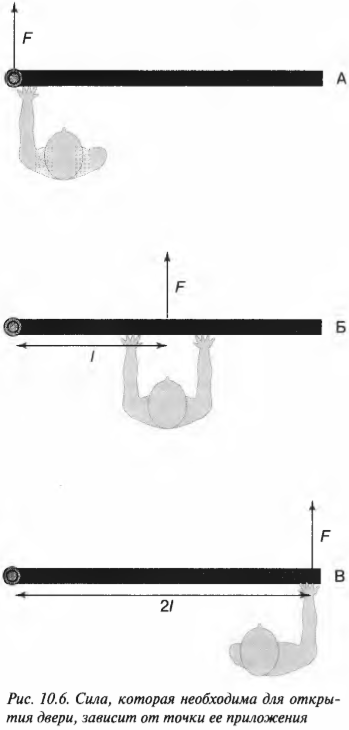
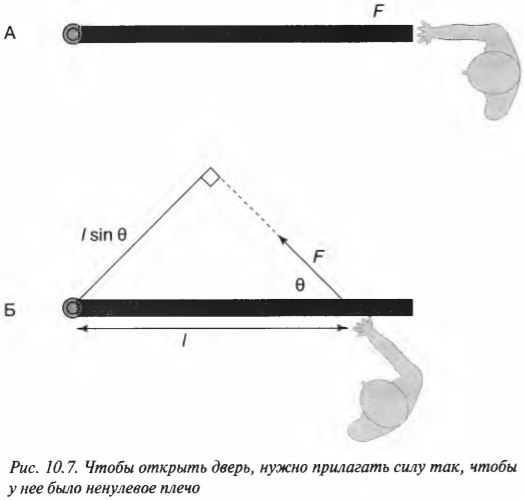
Предположим, что нам нужно открыть дверь, схематически показанную на рис. 10.6. Как известно из опыта, дверь практически невозможно открыть, если прилагать силу вблизи петель (см. схему А на рис. 10.6). Однако, если приложить силу посередине двери, то открыть ее будет гораздо проще (см. схему Б на рис. 10.6). Наконец, прилагая силу у противоположного края двери по отношению к расположению петель, ее можно открыть с еще меньшим усилием (см. схему В на рис. 10.6).
На рис. 10.6 расстояние от мест расположения петель до точки приложения силы и есть плечо силы. Моментом силы называется произведение прилагаемой силы ( F ) на плечо силы ( l ):
Момент силы в системе СИ измеряется в Н·м, а в системе СГС — в дин·см (подробнее эти системы единиц измерения описываются в главе 2).
Вернемся к примеру на рис. 10.6, где требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н. В случае А (см. рис. 10.6) плечо силы равно нулю и произведение этого плеча на силу любой величины (включая и силу 200 Н) даст нулевой момент силы. В случае Б (см. рис. 10.6) плечо силы равно половине ширины двери, т.е. плечо силы ( l ) равно 0,5 м и момент силы будет равен:
В случае В (см. рис. 10.6) плечо силы равно ширине двери, т.е. плечо силы ( l ) равно 1 м и момент силы будет равен:
Итак, увеличение вдвое длины плеча при той же силе дает нам такое же увеличение момента силы. До сих пор сила прилагалась перпендикулярно к линии, соединяющей точку приложения силы и точку вращения. А что будет с моментом силы, если дверь будет немного приоткрыта и направление силы уже будет не перпендикулярным?
Разбираемся с направлением приложенной силы и плечом силы
Допустим, что сила приложена не перпендикулярно к поверхности двери, а параллельно, как показано на схеме А на рис. 10.7. Как известно из опыта, таким образом дверь открыть невозможно. Дело в том, что у такой силы нет проекции, которая бы могла вызвать вращательное движение. Точнее говоря, у такой силы нет ненулевого плеча для создания вращательного момента силы.
Размышляем над тем, как создается момент силы
Момент силы из предыдущего примера требуется создавать всегда для открытия двери независимо от того, какую дверь приходится открывать: легкую калитку изгороди или массивную дверь банковского сейфа. Как вычислить необходимый момент силы? Сначала нужно определить плечо сил, а потом умножить его на величину силы.
Однако не всегда все так просто. Посмотрите на схему Б на рис. 10.7. Как видите, сила прилагается под некоторым углом ( theta ). Как в таком случае определить плечо силы? Если бы угол ( theta ) был прямым, то мы могли бы воспользоваться уже известно нам формулой:
Однако в данном случае угол ( theta ) не является прямым.
В таком случае нужно просто помнить следующее правило: плечом силы называется длина перпендикуляра, опущенного из предполагаемой точки вращения на прямую, относительно которой действует сила.
Попробуем применить это правило определения плеча силы для схемы Б на рис. 10.7. Нужно продлить линию, вдоль которой действует сила, а потом опустить на нее перпендикуляр из точки вращения двери. Из полученного прямоугольного треугольника легко определить искомое плечо силы:
Если угол ( theta ) равен нулю, то никакого момента силы не возникает (см. схему А на рис. 10.7).
Итак, получаем для момента силы для схемы Б на рис. 10.7:
Например, если требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н, приложенной под углом ( theta ) = 45°, то создаваемый момент этой силы будет равен:
Как видите, этот момент силы 140 Н·м меньше, чем момент силы 200 Н·м, созданный под прямым углом на схеме В на рис. 10.6.
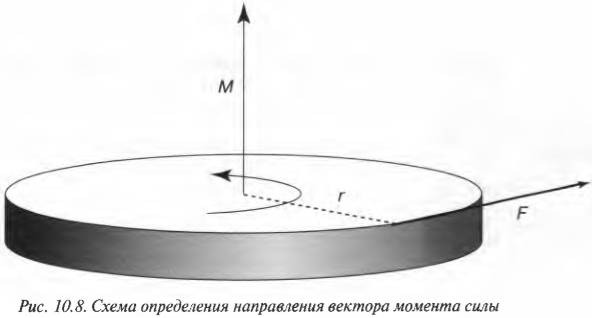
Определяем направление момента силы
Учитывая все приведенные выше сведения о моменте силы, у читателя вполне может возникнуть подозрение, что момент силы обладает направлением. И это действительно так. Момент силы является векторной величиной, направление которой определяется по правилу правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление силы, то вытянутый большой палец укажет направление вектора момента силы.
На рис. 10.8 показан пример силы ( mathbf{F} ) с плечом ( mathbf{l} ) и соответствующего вектора момента сил ( mathbf{M} ).
Уравновешиваем моменты сил
В жизни нам часто приходится сталкиваться с равновесными состояниями. Как равновесное механическое состояние определяется с точки зрения физики? Обычно физики подразумевают под равновесным состоянием объекта то, что он не испытывает никакого ускорения (но может двигаться с постоянной скоростью).
Для поступательного движения равновесное состояние означает, что сумма всех сил, действующих на объект равна нулю:
Иначе говоря, результирующая действующая сила равна нулю.
Вращательное движение также может быть равновесным, если такое движение происходит без углового ускорения, т.е. с постоянной угловой скоростью.
Для вращательного движения равновесное состояние означает, что сумма всех моментов сил, действующих на объект, равна нулю:
Как видите, это условие равновесного вращательного движения аналогично условию равновесного поступательного движения. Условия равновесного вращательного движения удобно использовать для определения момента силы, необходимого для уравновешивания неравномерно вращающегося объекта.
Простой пример: вешаем рекламный плакат
Предположим, что у входа в магазин нужно повесить большой и тяжелый рекламный плакат, как показано на рис. 10.9. Хозяин магазина пытался сделать это и раньше, но у него ничего не выходило, поскольку он использовал очень непрочный болт.
Попробуем определить силу, с которой болт должен удерживать всю конструкцию, показанную на рис. 10.9. Пусть плакат имеет массу 50 кг и висит на шесте 3 м от точки опоры шеста, а массу шеста в данном примере будем считать пренебрежимо малой. Болт находится в 10 см от точки опоры шеста.
Согласно условиям равновесия, сумма всех моментов сил должна быть равна нулю:
Иначе говоря:
где ( mathbf{M_п} ) — это момент силы со стороны плаката, а ( mathbf{M_б} ) — это момент силы со стороны болта.
Чему равны упомянутые моменты? Момент силы со стороны плаката можно легко определить по формуле:
где ( m ) = 50 кг — это масса плаката, ( mathbf{g} ) — ускорение свободного падения под действием силы гравитационного притяжения (силы тяжести), ( mmathbf{g} ) — сила тяжести плаката, а ( l_п ) = 3 м — это плечо силы тяжести плаката.
Подставляя значения, получим:
Обратите внимание, что здесь перед ускорением свободного падения под действием силы гравитационного притяжения стоит знак “минус”. Это значит, что вектор ускорения свободного падения направлен вниз, т.е. в сторону, противоположную выбранному направлению оси координат.
Момент силы со стороны болта определяется формулой:
где ( mathbf{F_б} ) — это искомая сила, с которой болт должен удерживать всю конструкцию, а ( l_б ) = 0,1 м — это ее плечо.
Подставляя полученные выражения для моментов сил в формулу:
получим, что:
Отсюда с помощью простых алгебраических преобразований получим искомую силу:
Как видите сила, с которой болт должен удерживать всю конструкцию, направлена противоположно вектору ускорения свободного падения, т.е. вверх.
Подставляя значения, получим искомый ответ:
Более сложный пример: учитываем силу трения при расчете равновесия
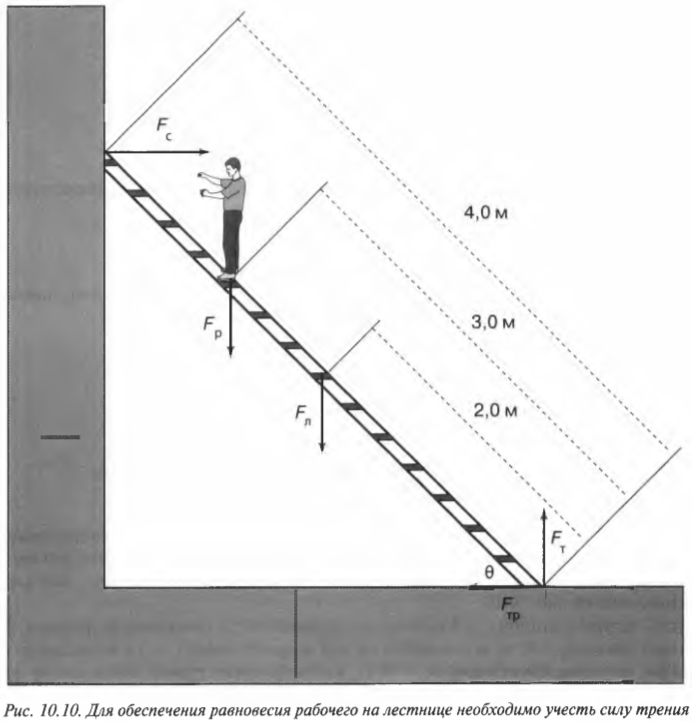
Рассмотрим теперь другую более сложную задачу, в которой для расчета равновесия системы объектов нужно учесть силу трения. Предположим, что работник магазина решил использовать переносную лестницу для монтажа рекламного плаката, как схематически показано на рис. 10.10.
Пусть лестница длиной ( l_л ) = 4 м стоит под углом ( theta ) = 45° к поверхности тротуара, работник имеет массу ( m_р ) = 45 кг и находится на ней на расстоянии ( l_р ) = 3 м от нижнего конца лестницы, лестница имеет массу (m_л ) = 20 кг, а коэффициент трения покоя между поверхностью тротуара и концами лестницы равен ( mu_п ) = 0,7. Вопрос: будет ли такая система объектов находиться в состоянии равновесия? Попросту говоря, достаточной ли будет сила трения, чтобы лестница вместе с рабочим не соскользнула и упала?
Итак, для ответа на этот вопрос нам нужно учесть следующие силы, действующие на лестницу:
- ( mathbf{F_с} ) — нормальная сила со стороны стены;
- ( mathbf{F_р} ) — вес рабочего;
- ( mathbf{F_л} ) — вес лестницы;
- ( mathbf{F_{тр}} ) — сила трения между поверхностью тротуара и концами лестницы;
- ( mathbf{F_т} ) — нормальная сила со стороны тротуара.
Согласно условиям равновесного поступательного движения, сумма всех сил, действующих на лестницу, должна быть равна нулю:
Это значит, что сумма всех сил вдоль горизонтальной оси, а именно нормальной силы со стороны стены ( mathbf{F_с} ) и силы трения между поверхностью тротуара и концами лестницы ( mathbf{F_{тр}} ), должна быть равна нулю, то есть:
или
Перефразируя поставленный выше вопрос о достаточности силы трения, получим: выполняется ли условие
Кроме того, сумма всех сил вдоль вертикальной оси, а именно веса рабочего ( mathbf{F_р} ), веса лестницы ( mathbf{F_л} ) и нормальной силы со стороны тротуара ( mathbf{F_т} ), должна быть равна нулю, то есть:
или
Согласно условиям равновесного вращательного движения, также необходимо равенство нулю всех моментов сил, действующих на лестницу:
Пусть предполагаемой точкой вращения является нижний конец лестницы, тогда должна быть равна нулю сумма моментов сил, создаваемых весом рабочего ( mathbf{M_р=[L_р!times! F_р]} ), весом лестницы ( mathbf{M_л=[L_л!times!F_л]} ) и нормальной силой со стороны стены ( mathbf{M_с=[L_с!times! F_с]} ):
или
или
Поскольку ( L_р=l_р ), ( L_л=l_л/2 ) (центр тяжести лестницы находится посередине лестницы), ( L_с=l_л ), ( alpha=360^{circ}-theta ), ( beta=360^{circ}-theta ) и ( gamma=theta ), то получим:
или
Таким образом, мы получили систему из двух уравнений с двумя неизвестными сил ( mathbf{F_с} ) и ( mathbf{F_т} ):
Зададимся вопросом: соблюдается ли условие
Из системы двух уравнений получим:
Итак, остается выяснить, соблюдается ли условие:
После подстановки значений получим:
Поскольку ( mu_т ) = 0,7, то упомянутое условие соблюдается, и лестница с рабочим не упадет.
Глава 10. Вращаем объекты: момент силы
3.5 (69.52%) 42 votes