Download Article
Download Article
A pentagon is a polygon with five straight sides. Almost all problems you’ll find in math class will cover regular pentagons, with five equal sides. There are two common ways to find the area, depending on how much information you have.
-
1
Start with the side length and apothem. This method works for regular pentagons, with five equal sides. Besides the side length, you’ll need the «apothem» of the pentagon. The apothem is the line from the center of the pentagon to a side, intersecting the side at a 90º right angle.[1]
- A regular pentagon can be divided into five triangles.[2]
- Where the height of the triangle is known as the apothem.[3]
- Then, using the apothem, the area of a regular pentagon will be ½ x apothem x 5.[4]
- Don’t confuse the apothem with the radius, which touches a corner (vertex) instead of a midpoint. If you only know the side length and radius, skip down to the next method instead.
- We’ll use an example pentagon with side length 3 units and apothem 2 units.
- A regular pentagon can be divided into five triangles.[2]
-
2
Divide the pentagon into five triangles. Draw five lines from the center of the pentagon, leading to each vertex (corner). You now have five triangles.[5]
Advertisement
-
3
Calculate the area of a triangle. Each triangle has a base equal to the side of the pentagon. It also has a height equal to the pentagon’s apothem. (Remember, the height of a triangle runs from a vertex to the opposite side, at a right angle.) To find the area of any triangle, just calculate ½ x base x height.[6]
- In our example, area of triangle = ½ x 3 x 2 = 3 square units.
-
4
Multiply by five to find the total area. We’ve divided the pentagon into five equal triangles. To find the total area, just multiply the area of one triangle by five.[7]
- In our example, A(total pentagon) = 5 x A(triangle) = 5 x 3 = 15 square units.
Advertisement
-
1
Start with just the side length. This method only works for regular pentagons, which have five sides of equal length.
- In this example, we’ll use a pentagon with side length 7 units.
-
2
Divide the pentagon into five triangles. Draw a line from the center of the pentagon to any vertex. Repeat this for every vertex. You now have five triangles, each the same size.[8]
-
3
Divide a triangle in half. Draw a line from the center of the pentagon to the base of one triangle. This line should hit the base at a 90º right angle, dividing the triangle into two equal, smaller triangles.[9]
-
4
Label one of the smaller triangles. We can already label one sides and one angle of the smaller triangle:
- The base of the triangle is ½ the side of the pentagon. In our example, this is ½ x 7 = 3.5 units.
- The angle at the pentagon’s center is always 36º. (Starting with a full 360º center, you could divide it into 10 of these smaller triangles. 360 ÷ 10 = 36, so the angle at one triangle is 36º.)
-
5
Calculate the height of the triangle. The height of this triangle is the side at right angles to the pentagon’s edge, leading to the center. We can use beginning trigonometry to find the length of this side:[10]
- In a right-angle triangle, the tangent of an angle equals the length of the opposite side, divided by the length of the adjacent side.
- The side opposite the 36º angle is the base of the triangle (half the pentagon’s side). The side adjacent to the 36º angle is the height of the triangle.
- tan(36º) = opposite / adjacent
- In our example, tan(36º) = 3.5 / height
- height x tan(36º) = 3.5
- height = 3.5 / tan(36º)
- height = (about) 4.8 units.
-
6
Find the area of the triangle. A triangle’s area equals ½ the base x the height. (A = ½bh.) Now that you know the height, plug in these values to find the area of your small triangle.
- In our example, Area of small triangle = ½bh = ½(3.5)(4.8) = 8.4 square units.
-
7
Multiply to find the area of the pentagon. One of these smaller triangles covers 1/10 of the pentagon’s area. To find the total area, multiply the area of the smaller triangle by 10.
- In our example, the area of the whole pentagon = 8.4 x 10 = 84 square units.
Advertisement
-
1
Use the perimeter and apothem. The apothem is a line from the center of a pentagon, that hits a side at a right angle. If you are given its length, you can use this easy formula
- Area of a regular pentagon = pa/2, where p = the perimeter and a = the apothem.[11]
- If you don’t know the perimeter, calculate it from the side length: p = 5s, where s is the side length.
- Area of a regular pentagon = pa/2, where p = the perimeter and a = the apothem.[11]
-
2
Use the side length. If you only know the side length, use the following formula:[12]
- Area of a regular pentagon = (5s2) / (4tan(36º)), where s = side length.
- tan(36º) = √(5-2√5).[13]
So if your calculator doesn’t have a «tan» function, use the formula Area = (5s2) / (4√(5-2√5)).
-
3
Choose a formula that uses radius only. You can even find the area if you only know the radius. Use this formula:[14]
- Area of a regular pentagon = (5/2)r2sin(72º), where r is the radius.
Advertisement
Add New Question
-
Question
How do I find the perimeter of a pentagon when I’m only given the apothem?
The perimeter of a regular pentagon is the apothem multiplied by 7.267.
-
Question
What would be the length of a side of a regular pentagon with a perimeter of 12.5?
Each side of a regular pentagon is one-fifth of the perimeter. So in this case, each side measures 12.5 / 5 = 2.5.
-
Question
I am struggling to find the length of one side of a pentagon; two sides are 0.9 meters, 2 other sides at 0.53 meters each.
There is no formula available for finding a side of an irregular pentagon.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Irregular pentagons, or pentagons with unequal sides, are more difficult to study. The best approach is usually to divide the pentagon into triangles, and add up the area of each triangle. You may also need to draw a larger shape around the pentagon, calculate its area, and subtract the area of the extra space.
-
The examples given here use rounded values to make the math simpler. If you measure a real polygon with the given side length, you’ll get slightly different results for the other lengths and area.
-
If possible, use both a geometric method and a formula method, and compare results to confirm that you have the right answer. You may get slightly different answers if you enter the formula all at once (since you won’t round along the way), but they should be very close.
Show More Tips
Advertisement
References
About This Article
Article SummaryX
It’s easiest to find the area of a regular pentagon if you know the length of a side and the apothem. The apothem is a line that intersects one of the sides from the center of the pentagon at a 90° angle. For example, let’s say you have a pentagon with a side length of 3 units and an apothem of 2 units. You can now divide the pentagon into 5 triangles, each with a base width of 3 (equal to the length of one side of the pentagon) and a height of 2 (equal to the apothem). To find the area of the pentagon, all you need to do is find the area of one of the triangles and multiply the result by 5. Use the formula ½ x base x height to find the area of each triangle. In this example, ½ x 3 x 2 = 3, so each triangle has an area of 3 square units. Multiply 3 x 5 to get 15 square units, or the area of the entire pentagon. You can also use the formula Area = Pa/2, where P is the perimeter of the pentagon and a is the apothem. In the example above, the perimeter would be 3 x 5 = 15, and the apothem is 2. (15 x 2)/2 = 30/2, which is equal to 15. If you only know the side length of the pentagon, you can still figure out the area, but you’ll need to do a bit of trigonometry. Start by dividing the pentagon into 5 equal triangles, starting from a point at the center of the pentagon. The base of each triangle will be equal to the length of a side of the pentagon. Now, divide one of the triangles in half by drawing a vertical line from the vertex to the middle of the base to create two right triangles. You know that the base of the smaller triangle is ½ of the side length of the pentagon. So, if you have a pentagon with a side length of 7 units, the base of the smaller right triangle is 3.5 units. When you’re working with a regular pentagon, the angle at the top of this triangle will always be 36°. To find the height of the triangle, use the formula tan36° = b (base)/h (height) and solve for h. In our example, tan36° = 3.5/h. Multiply tan36° by h, then divide 3.5 by tan36° to find the height, which is approximately 4.8 units. Now you can plug the height into the formula for the area of a triangle, 1/2 x b x h, to find the area of the triangle. Plug in the base of the larger triangle for the b variable and the height you just found for the h variable to get ½ x 7 x 4.8 = 16.8 square units. Then, multiply the area of the larger triangle by 5 to get the full area of the pentagon, or 84 square units. Alternatively, you can plug the base width of the smaller triangle into the formula for the area of a triangle, then multiply the result by 10. Either way, you’ll get the same answer. You can also calculate the area from only the side length using the formula 5s2/4tan36°, where s is the length of one side of the pentagon. If you don’t have a calculator with a tangent function, don’t worry. Tan36° = √(5-2√5), so you can plug that into your calculations in place of tan36°. You can also figure out the area of a pentagon using only the radius, or r, which is the distance from the center of the pentagon to one of the corners, or vertices. To do this, use the formula 5/2 x r^2 x sin72°. For more on finding the area of a regular pentagon, including using formulas if you only know the length of a side or the radius, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 806,136 times.
Reader Success Stories
-
Abraham Edgar
Jun 6, 2016
«In method 2, finding the value of the angle helped me.»
Did this article help you?
Загрузить PDF
Загрузить PDF
Пятиугольник — это многоугольник, у которого пять углов. В подавляющем большинстве задач вы столкнетесь с правильным пятиугольником, у которого все стороны равны. Есть два основных способа найти площадь пятиугольника (в зависимости от известных вам величин).
-
1
Даны сторона и апофема. Этот метод применим к правильным пятиугольникам, у которых все стороны равны. Апофема — это отрезок, соединяющий центр пятиугольника и середину любой из его сторон; апофема всегда перпендикулярна стороне пятиугольника.
- Не путайте апофему с радиусом описанной окружности. Такой радиус — это отрезок, соединяющий центр пятиугольника с его вершиной (а не серединой стороны). Если вам дана сторона и радиус описанной окружности, перейдите к следующей главе.
- Например, дан пятиугольник со стороной 3 см и апофемой 2 см.
-
2
Разделите пятиугольник на пять равных треугольников. Для этого соедините центр пятиугольника с каждой из его вершин.
-
3
Вычислите площадь треугольника. Основание каждого треугольника — это сторона пятиугольника, а высота каждого треугольника — это апофема пятиугольника. Для вычисления площади треугольника перемножьте половину основания и высоту, то есть площадь = ½ х основание х высоту.
- В нашем примере площадь треугольника = ½ х 3 х 2 = 3 квадратных сантиметра.
-
4
Умножьте найденную площадь треугольника на 5, чтобы вычислить площадь пятиугольника. Это верно, так как мы разделили пятиугольник на пять равных треугольников.
- В нашем примере площадь пятиугольника = 5 х площадь треугольника = 5 х 3 = 15 квадратных сантиметров.
Реклама
-
1
Если дана сторона. Этот метод применим к правильным пятиугольникам, у которых все стороны равны.
- Например, дан пятиугольник со стороной 7 см.
-
2
Разделите пятиугольник на пять равных треугольников. Для этого соедините центр пятиугольника с каждой из его вершин.
-
3
Разделите треугольник пополам. Для этого из вершины треугольника, которая лежит в центре пятиугольника, опустите перпендикуляр к противоположной стороне треугольника, которая равна стороне пятиугольника. Вы получите два равных прямоугольных треугольника.
-
4
Дайте обозначения одному из прямоугольных треугольников.
- Основание прямоугольного треугольника — это половина стороны пятиугольника. В нашем примере основание равно ½ х 7 = 3,5 см.
- Угол вокруг центра пятиугольника равен 360˚. Разделив пятиугольник на пять равных треугольников, а потом разделив каждый треугольник пополам, вы поделите угол вокруг центра пятиугольника на 10 равных частей, то есть угол прямоугольного треугольника, противолежащий основанию, равен 360°/10 = 36˚.
-
5
Вычислите высоту треугольника. Высота прямоугольного треугольника равна его катету, отличному от основания. Используйте тригонометрические функции, чтобы найти высоту треугольника.[1]
- В прямоугольном треугольнике тангенс угла равен отношению противолежащей стороны к прилежащей стороне.
- В нашем примере для угла в 36˚ противолежащей стороной является основание, а прилежащей — высота.
- tg 36˚ = противолежащая сторона/прилежащая сторона
- В нашем примере tg 36˚ = 3,5/высота
- Высота х tg 36˚ = 3,5
- Высота = 3,5/tg 36˚
- Высота = 4,8 см (примерно)
-
6
Найдите площадь треугольника. Площадь треугольника = ½ х основание х высота (А = ½bh). Зная основание и высоту, вы можете найти площадь прямоугольного треугольника.
- В нашем примере площадь прямоугольного треугольника = ½bh = ½(3,5)(4,8) = 8,4 квадратных сантиметров.
-
7
Умножьте найденную площадь прямоугольного треугольника на 10, чтобы вычислить площадь пятиугольника. Это верно, так как мы разделили пятиугольник на десять равных прямоугольных треугольников.
- В нашем примере площадь пятиугольника равна 8,4 х 10 = 84 квадратных сантиметра.
Реклама
-
1
Даны периметр и апофема. Апофема — это отрезок, соединяющий центр пятиугольника и середину любой из его сторон; апофема всегда перпендикулярна стороне пятиугольника.
- A = ра/2, где р — периметр, а — апофема. [2]
- Если дана сторона, вычислите периметр правильного пятиугольника по формуле: p = 5s, где s — сторона пятиугольника.
- A = ра/2, где р — периметр, а — апофема. [2]
-
2
Дана сторона. Если дана только сторона пятиугольника, используйте следующую формулу:[3]
- А = (5s2) / (4tg36˚), где s — сторона пятиугольника.
- tg36˚ = √(5-2√5).[4]
Если на калькуляторе нет функции тангенса, используйте следующую формулу: А = (5s2) / (4√(5-2√5)).
-
3
Дан радиус описанной окружности. В этом случае для вычисления площади пятиугольника используйте следующую формулу:[5]
- A = (5/2)r2sin72˚, где r — радиус описанной окружности.
Реклама
Советы
- Сложнее работать с неправильным пятиугольником (это пятиугольник, стороны которого имеют разную длину). В этом случае разделите пятиугольник на треугольники, найдите их площади и сложите значения площадей. Вы также можете обрисовать пятиугольник правильной фигурой, вычислить ее площадь, а затем вычесть площадь дополнительного пространства.
- Формулы, полученные геометрическим путем, аналогичны формулам, которые описаны в этой статье. Подумайте, сможете ли вы вывести эти формулы. Формулу, включающую радиус описанной окружности, вывести труднее (намек: рассматривайте удвоенный угол при центре пятиугольника).
- В приведенных в этой статье примерах используются округленные значения, чтобы упростить вычисления. Если вы работаете с реальным многоугольником, то вы получите другие результаты для других длин и площадей.
- Если возможно, вычислите площадь пятиугольника, используя оба описанных метода. Затем сравните результаты, чтобы подтвердить правильность ответа.
Реклама
Об этой статье
Эту страницу просматривали 235 588 раз.
Была ли эта статья полезной?
Пятиугольник, виды, свойства и формулы.
Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.
Пятиугольник, выпуклый и невыпуклый пятиугольник
Правильный многоугольник
Свойства правильного пятиугольника
Построение правильного пятиугольника
Формулы правильного пятиугольника
Правильный пятиугольник в природе, технике и культуре
Пятиугольник, шестиугольник, семиугольник, восьмиугольник
Пятиугольник, выпуклый и невыпуклый пятиугольник:
Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.
Пятиугольник – фигура, состоящая из пяти углов (вершин), которые образуются пятью отрезками (сторонами).
Пятиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый пятиугольник – это пятиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый пятиугольник
Сумма внутренних углов любого выпуклого шестиугольника равна 540°.
Невыпуклый пятиугольник – это пятиугольник, у которого одна часть его точек лежат по одну сторону, а другая часть – по другую от любой прямой, проходящей через две его соседние вершины.
Рис. 2. Невыпуклый пятиугольник
Звёздчатый пятиугольник (пентаграмма) – пятиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого пятиугольника могут пересекаться между собой.
Правильный многоугольник:
Правильный пятиугольник (пентагон) – это правильный многоугольник с пятью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный пятиугольник – это пятиугольник, у которого все стороны равны, а все внутренние углы равны 108°.
Рис. 3. Правильный пятиугольник
Правильный пятиугольник имеет 5 сторон, 5 углов и 5 вершин.
Углы правильного семиугольника образуют семь равнобедренных треугольников.
Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны.
Свойства правильного пятиугольника:
1. Все стороны правильного пятиугольника равны между собой.
a1 = a2 = a3 = a4= a5.
2. Все углы равны между собой и каждый угол равен 108°.
α1 = α2 = α3 = α4 = α5 = 108°.
Рис. 4. Правильный пятиугольник
3. Сумма внутренних углов правильного пятиугольника равна 540°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного пятиугольника O.
Рис. 5. Правильный пятиугольник
5. Количество диагоналей правильного пятиугольника равно 5.
Рис. 6. Правильный пятиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр пятиугольника O.
Рис. 7. Правильный пятиугольник
7. Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
Рис. 8. Правильный пятиугольник
8. Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
a / c ≈ 5 / 8 ≈ 0,618.
Рис. 9. Правильный пятиугольник
Построение правильного пятиугольника:
Метод построения правильного пятиугольника вписыванием его в заданную окружность:
1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O.
2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
4. Постройте точку C посередине между O и B.
5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
9. Постройте правильный пятиугольник AEGHF.
Формулы правильного пятиугольника:
Пусть a – сторона пятиугольника, r – радиус окружности, вписанной в пятиугольник, R – радиус описанной окружности пятиугольника, S – площадь пятиугольника, h – высота пятиугольника, d – диагональ пятиугольника, Ф – отношение золотого сечения.
Формулы площади правильного пятиугольника:
Формулы высоты правильного пятиугольника:
Формулы стороны правильного пятиугольника:
Формулы диагонали правильного пятиугольника:
Формулы радиуса окружности, вписанной в правильный пятиугольник:
Формулы радиуса окружности, описанной вокруг правильного пятиугольника:
Правильный пятиугольник в природе, технике и культуре:
Пентасимметрию можно наблюдать в некоторых фруктах (например, у мушмулы германской), у иглокожих (например, у морских звёзд) и у некоторых растений.
Исследования формирования водяного льда на ровной поверхности меди при температурах 100-140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.
Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.
Паркет, тротуарная плитка, мозайки и т.п. может выкладываться элементами, которые имеют вид пятиугольников.
Государственный знак качества СССР имеет форму пятиугольника с выпуклыми сторонами.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Пятиугольник
Шестиугольник
Семиугольник
Восьмиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
9 666
Площадь правильного пятиугольника
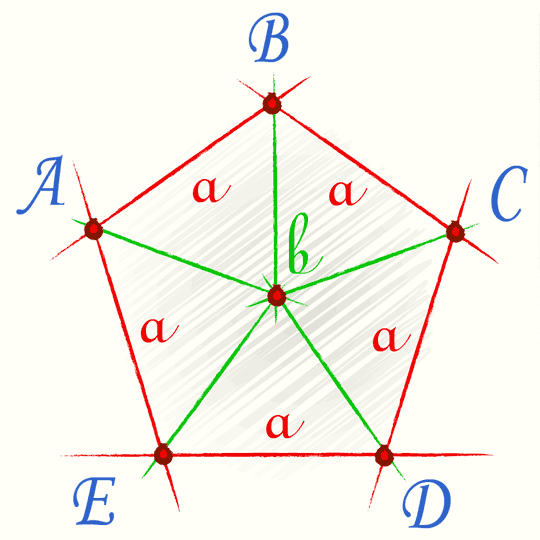
Нарисуем правильный пятиугольник.
Площадь правильного пятиугольника
Как мы видим он состоит из пяти равных равнобедренных треугольников с основанием a и бедрами b.
Если мы знаем только размер стороны a правильного пятиугольника, то размер b легко находится по формуле
радиуса описанной окружности правильного пятиугольника.
Таким образом получаем следующий вывод формулы:
[ b = frac{a}{2 sin(π/5)} ]
[ S_{равнобедр.треуг} = frac{a sqrt{b^2-frac{a^2}{4}}}{2}]
[ S_{равнобедр.треуг} = frac{1}{2} a sqrt{Big(frac{a}{2 sin(π/5)}Big)^2-frac{a^2}{4}}]
[ S = 5 S_{равнобедр.треуг} ]
[ S = frac{5}{2} a sqrt{Big(frac{a}{2 sin(π/5)}Big)^2-frac{a^2}{4}} ]
Вычислить, найти площадь правильного пятиугольника по формуле (5)
Площадь правильного пятиугольника |
стр. 321 |
|---|
Площадь правильного пятиугольника — это число, характеризующее правильный пятиугольник в единицах измерения площади.
Правильный пятиугольник (пентагон) — это пятиугольник, у которого все стороны и углы равны.
Обозначения[править]
Введём обозначения:
a — длина стороны;
n — число сторон, n = 5;
r — радиус вписанной окружности;
R — радиус описанной окружности;
α — половинный центральный угол, α = π/5;
P5 — периметр правильного пятиугольника;
SΔ — площадь равнобедренного треугольника с основанием, равным стороне, и боковыми сторонами, равными радиусу описанной окружности;
S5 — площадь правильного пятиугольника.
Формулы[править]
Применима формула для площади правильного n-угольника при n=5:
Используя значения тригонометрических функций углов для угла α=π/5:
где 



Другие многоугольники[править]
- Площадь равностороннего треугольника;
- Площадь квадрата;
- Площадь правильного пятиугольника;
- Площадь правильного шестиугольника;
- Площадь правильного восьмиугольника;
- Площадь правильного десятиугольника;
- Площадь правильного двенадцатиугольника;
- Площадь правильного шестнадцатиугольника;
- Площадь правильного двадцатиугольника;
- Площадь правильного n-угольника.