Площадь боковой поверхности додекаэдра Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Длина ребра додекаэдра: 10 метр —> 10 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
1720.47740058897 Квадратный метр —> Конверсия не требуется
12 Площадь боковой поверхности додекаэдра Калькуляторы
8 Площадь додекаэдра Калькуляторы
Площадь боковой поверхности додекаэдра формула
Площадь боковой поверхности додекаэдра = 5/2*sqrt(25+(10*sqrt(5)))*Длина ребра додекаэдра^2
LSA = 5/2*sqrt(25+(10*sqrt(5)))*le^2
Математические характеристики додекаэдра

Радиус описанной сферы додекаэдра
где a — длина стороны.
Сфера может быть вписана внутрь додекаэдра.
Радиус вписанной сферы додекаэдра
Площадь поверхности додекаэдра.
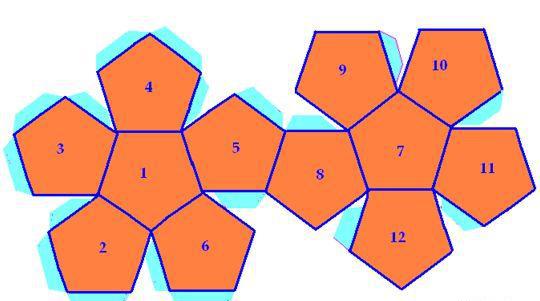
Для наглядности площадь поверхности додекаэдра можно представить в виде площади развёртки.
Площадь поверхности можно определить как площадь одной из сторон додекаэдра (это площадь правильного пятиугольника) умноженной на 12. Либо воспользоваться формулой:
Объем додекаэдра определяется по следующей формуле:
Правильные многогранники
Существует всего пять правильных многогранников:
- Тетраэдр
- Куб (Гексаэдр)
- Октаэдр
- Икосаэдр
- Додекаэдр
Если какое-то из этих названий звучит для тебя как древний эльфийский язык, обязательно прочитай эту статью!
Давай посмотрим, как они выглядят, и разберем основные формулы – площади поверхности, объема, радиусов вписанной и описанной сферы.
А также решим задачу №8.
О том, как рисовать пространственные фигуры на плоскости, можно прочитать в нашей статье: «Изображение пространственных фигур. Визуальный гид».
Поехали!
Правильные многогранники — подробнее
Многогранник называется правильным, если:
- он выпуклый;
- все его грани являются правильными многоугольниками;
- в каждой его вершине сходится одинаковое число его ребер.
Пять правильных многогранников
Тетраэдр
Тетраэдр состоит из четырёх равносторонних треугольников.
Фигура имеет 4 грани, 4 вершины и 6 ребер(a).
Площадь поверхности тетраэдра:
( displaystyle S={{a}^{2}}sqrt{3})
Объем тетраэдра:
( displaystyle V=frac{{{a}^{3}}}{12}sqrt{2})
Радиус описанной вокруг тетраэдра сферы:
( displaystyle R=frac{a}{4}sqrt{6})
Радиус вписанной в тетраэдр сферы:
( displaystyle R=frac{a}{12}sqrt{6})
Куб (Гексаэдр)
Куб состоит из шести квадратов.
Фигура имеет 6 граней, 8 вершин и 12 ребер (a).
Площадь поверхности куба:
( displaystyle S=6{{a}^{2}})
Объем куба:
( displaystyle V={{a}^{3}})
Радиус описанной вокруг куба сферы:
( displaystyle R=frac{a}{2}sqrt{3})
Радиус вписанной в куб сферы:
( displaystyle r=frac{a}{2})
Октаэдр
Октаэдр составлен из восьми равносторонних треугольников.
Фигура имеет 8 граней, 6 вершин и 12 ребер (a).
Площадь поверхности октаэдра:
( displaystyle S=2{{a}^{2}}sqrt{3})
Объем октаэдра:
( displaystyle V=frac{{{a}^{3}}}{3}sqrt{2})
Радиус описанной вокруг октаэдра сферы:
( displaystyle R=frac{a}{2}sqrt{2})
Радиус вписанной в октаэдр сферы:
( displaystyle r=frac{a}{6}sqrt{6})
Икосаэдр
Икосаэдр составлен из двадцати равносторонних треугольников.
Фигура имеет 20 граней, 12 вершин и 30 ребер (a).
Площадь поверхности икосаэдра:
( displaystyle S=5{{a}^{2}}sqrt{3})
Объем икосаэдра:
( displaystyle V=frac{5{{a}^{3}}}{12}left( 3+sqrt{5} right))
Радиус описанной вокруг икосаэдра сферы:
( displaystyle R=frac{a}{4}sqrt{2left( 5+sqrt{5} right)})
Радиус вписанной в икосаэдр сферы:
( displaystyle r=frac{a}{4sqrt{3}}left( 3+sqrt{5} right))
Додекаэдр
Додекаэдр составлен из двенадцати равносторонних пятиугольников.
Фигура имеет 12 граней, 20 вершин и 30 ребер (a).
Площадь поверхности додекаэдра:
( displaystyle S=3{{a}^{2}}sqrt{5left( 5+2sqrt{5} right)})
Объем додекаэдра:
( displaystyle V=frac{{{a}^{3}}}{4}left( 15+7sqrt{5} right))
Радиус описанной вокруг додекаэдра сферы:
( displaystyle R=frac{a}{4}left( 1+sqrt{5} right)sqrt{3})
Радиус вписанной в додекаэдр сферы:
( displaystyle r=frac{a}{4}sqrt{10+frac{22}{sqrt{5}}})
Решение задачи №8 на тему «Правильные многогранники»
Задача:
В кубе ( displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) с ребром ( displaystyle sqrt{12}) найдите ( displaystyle A{{C}_{1}}).
Решение:
( displaystyle d=asqrt{3}),
где ( displaystyle d) – диагональ куба,( displaystyle a) – сторона куба.( displaystyle A{{C}_{1}}) – это и есть диагональ куба.
Тогда ( displaystyle A{{C}_{1}}=asqrt{3}=sqrt{12}cdot sqrt{3}=sqrt{36}=6).
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Додекаэдр – это объемная геометрическая фигура, которая имеет 12 граней. Это основная его характеристика, поскольку количество вершин и число ребер могут изменяться. Рассмотрим в статье свойства этой фигуры, ее использование в настоящее время, а также некоторые интересные исторические факты, связанные с ней.
Общие понятия о фигуре
Додекаэдр – это слово взято из языка древних греков, которое буквально означает «фигура с 12-ю гранями». Его грани представляют собой многоугольники. Учитывая свойства пространства, а также определение додекаэдра, можно сказать, что его многоугольники могут иметь 11 сторон и меньше. Если грани фигуры образованы правильными пентагонами (многоугольник, имеющий 5 сторон и 5 вершин), то такой додекаэдр называется правильным, он входит в число 5-ти платоновских объектов.
Геометрические свойства правильного додекаэдра
Рассмотрев вопрос о том, что такое додекаэдр, можно перейти к характеристике основных свойств правильной объемной фигуры, то есть образованной одинаковыми пятиугольниками.
Поскольку рассматриваемая фигура является объемной, выпуклой и состоит из многоугольников (пентагонов), то для нее справедливо правило Эйлера, которое устанавливает однозначную зависимость между числом граней, ребер и вершин. Оно записывается в виде: Г + В = Р + 2, где Г – количество граней, В – вершин, Р – ребер. Зная, что правильный додекаэдр – это двенадцатигранник, число вершин которого составляет 20, то, используя правило Эйлера, получаем: Р = Г + В — 2 = 30 ребер. Углы между соседними гранями этой платоновской фигуры являются одинаковыми, они равны 116,57o.
Математические формулы для правильного додекаэдра
Ниже приведем основные формулы додекаэдра, который состоит из правильных пятиугольников. Эти формулы позволяют вычислить площадь его поверхности, объем, а также определить радиусы сфер, которые можно вписать в фигуру или описать вокруг нее:
- Площадь поверхности додекаэдра, которая представляет собой произведение 12-ти площадей пятиугольников со стороной «a», выражается следующей формулой: S = 3*√(25 + 10*√5)*a2. Для приблизительных расчетов можно пользоваться выражением: S = 20,65*a2.
- Объем правильного додекаэдра, как и его суммарная площадь граней, однозначно определяется из знания стороны пятиугольника. Эта величина выражается следующей формулой: V = 1/4*(15 + 7*√5)*a3, что приблизительно равно: V = 7,66*a3.
- Радиус вписанной окружности, которая касается внутренней стороны граней фигуры в их центре, определяется так: R1 = 1/4*a*√((50 + 22*√5)/5), или приблизительно R1 = 1,11*a.
- Описанную окружность проводят через 20 вершин правильного додекаэдра. Ее радиус определяется формулой: R2 = √6/4*a*√(3 + √5), или приблизительно R2 = 1,40*a. Приведенные цифры говорят, что радиус внутренней сферы, вписанной в додекаэдр, составляет 79 % от такового для описанной сферы.
Симметрия правильного додекаэдра
Как видно из рисунка выше, додекаэдр – это достаточно симметричная фигура. Для описания этих свойств в кристаллографии вводят понятия об элементах симметрии, главными из которых являются поворотные оси и плоскости отражения.
Идея использования этих элементов проста: если установить ось внутри рассматриваемого кристалла, а затем повернуть его вокруг этой оси на некоторый угол, то кристалл полностью совпадет сам с собой. То же самое относится к плоскости, только операцией симметрии здесь является не поворот фигуры, а ее отражение.
Для додекаэдра характерны следующие элементы симметрии:
- 6 осей пятого порядка (то есть поворот фигуры осуществляется на угол 360/5 = 72o), которые проходят через центры расположенных напротив друг друга пятиугольников;
- 15 осей второго порядка (симметричный угол поворота равен 360/2 = 180o), которые соединяют середины противоположных ребер октаэдра;
- 15 плоскостей отражения, проходящих через расположенные напротив ребра фигуры;
- 10 осей третьего порядка (операция симметрии осуществляется при повороте на угол 360/3 = 120o), которые проходят через противоположные вершины додекаэдра.
Современное использование додекаэдра
В настоящее время геометрические объекты в форме додекаэдра находят применение в некоторых сферах деятельности человека:
- Игральные кости для настольных игр. Так как додекаэдр – это платоновская фигура, обладающая высокой симметрией, то объекты этой формы можно использовать в играх, где продолжение событий имеет вероятностный характер. Игральные кости в своем большинстве изготавливают кубической формы, поскольку их сделать проще всего, однако современные игры становятся все сложнее и разнообразнее, а значит, требуют костей с большим количеством возможностей. Кости в форме додекаэдра применяются в ролевой настольной игре Dungeons and Dragons. Особенностью этих костей является то, что сумма цифр, расположенных на противоположных гранях, всегда равна 13.
- Источники звука. Современные звуковые колонки часто изготавливают в форме додекаэдра, поскольку они распространяют звук во всех направлениях и защищают его от окружающего шума.
Историческая справка
Как выше было сказано, додекаэдр – это одно из пяти платоновых тел, которые характеризуются тем, что образованы одинаковыми правильными многогранниками. Остальными четырьмя платоновыми телами являются тетраэдр, октаэдр, куб и икосаэдр.
Упоминания о додекаэдре относятся еще к вавилонской цивилизации. Однако первое подробное изучение его геометрических свойств сделали древнегреческие философы. Так, Пифагор в качестве эмблемы своей школы использовал пятиконечную звезду, построенную на вершинах пентагона (грани додекаэдра).
Платон подробно охарактеризовал правильные объемные фигуры. Философ считал, что они представляют главные стихии: тетраэдр – это огонь; куб – земля; октаэдр – воздух; икосаэдр – вода. Поскольку додекаэдру не досталась никакая стихия, то Платон предположил, что он описывает развитие всей Вселенной.
Мысли Платона многие могут посчитать примитивными и псевдонаучными, однако вот что любопытно: современные исследования наблюдаемой Вселенной показывают, что приходящее на Землю космическое излучение обладает анизотропией (зависимостью от направления), и симметрия этой анизотропии хорошо согласуется с геометрическими свойствами додекаэдра.
Додекаэдр и сакральная геометрия
Священная геометрия представляет собой совокупность псевдонаучных (религиозных) знаний, которые приписывают различным геометрическим фигурам и символам определенное сакральное значение.
Значение многогранника додекаэдра в сакральной геометрии заключается в совершенности его формы, которую наделяют способностью приводить окружающие тела в гармонию и равномерно распределять энергию между ними. Додекаэдр считается идеальной фигурой для практики медитации, поскольку он играет роль проводника сознания в иную реальность. Ему приписывают способность снимать стресс у человека, восстанавливать память, улучшать внимание и концентрационные способности.
Римский додекаэдр
В середине XVIII века в результате некоторых археологических раскопок на территории Европы был найден странный предмет: он имел форму додекаэдра, сделанного из бронзы, его размеры составляли несколько сантиметров, и он был пустым внутри. Однако любопытно следующее: в каждой его грани было сделано отверстие, причем диаметр всех отверстий был различным. В настоящее время найдено более 100 таких объектов в результате раскопок во Франции, Италии, Германии и других стран Европы. Все эти предметы датируются II-III веком нашей эры и относятся к эпохе господства Римской Империи.
Как римляне использовали эти предметы — не известно, поскольку не найдено ни одного письменного источника, который бы содержал точное объяснение их назначения. Лишь в некоторых трудах Плутарха можно встретить упоминание, что эти объекты служили для понимания характеристик 12-ти знаков Зодиака. Современное объяснение тайны римских додекаэдров имеет несколько версий:
- предметы использовались в качестве подсвечников (внутри них найдены остатки воска);
- они применялись как игральные кости;
- додекаэдры могли служить календарем, который указывал на время посадки сельскохозяйственных культур;
- могли они применяться в качестве основы для крепления римского военного штандарта.
Существуют и другие версии использования римских додекаэдров, тем не менее ни одна из них не имеет точных доказательств. Известно лишь одно: древние римляне высоко ценили эти предметы, поскольку в раскопках они часто обнаруживаются в тайниках вместе с золотом и драгоценностями.
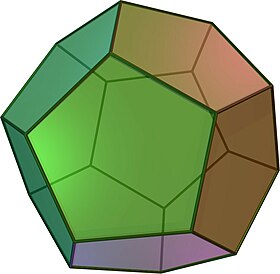
| Regular dodecahedron | |
|---|---|
 (Click here for rotating model) |
|
| Type | Platonic solid |
| Elements | F = 12, E = 30 V = 20 (χ = 2) |
| Faces by sides | 12{5} |
| Conway notation | D |
| Schläfli symbols | {5,3} |
| Face configuration | V3.3.3.3.3 |
| Wythoff symbol | 3 | 2 5 |
| Coxeter diagram | |
| Symmetry | Ih, H3, [5,3], (*532) |
| Rotation group | I, [5,3]+, (532) |
| References | U23, C26, W5 |
| Properties | regular, convex |
| Dihedral angle | 116.56505° = arccos(−1⁄√5) |
 5.5.5 (Vertex figure) |
 Regular icosahedron (dual polyhedron) |
 Net |
Animation of a net of a regular (pentagonal) dodecahedron being folded
3D model of a regular dodecahedron
Crystal structure of Co20L12 dodecahedron reported by Kai Wu, Jonathan Nitschke and co-workers at University of Cambridge in Nat. Synth. 2023, DOI:10.1038/s44160-023-00276-9 [1]
A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular, which is composed of 12 regular pentagonal faces, three meeting at each vertex. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges, and 160 diagonals (60 face diagonals, 100 space diagonals).[2] It is represented by the Schläfli symbol {5,3}.
Dimensions[edit]
If the edge length of a regular dodecahedron is 
(sequence A179296 in the OEIS)
and the radius of an inscribed sphere (tangent to each of the regular dodecahedron’s faces) is
while the midradius, which touches the middle of each edge, is
These quantities may also be expressed as
where ϕ is the golden ratio.
Note that, given a regular dodecahedron of edge length one, ru is the radius of a circumscribing sphere about a cube of edge length ϕ, and ri is the apothem of a regular pentagon of edge length ϕ.
Surface area and volume[edit]
The surface area A and the volume V of a regular dodecahedron of edge length a are:
Additionally, the surface area and volume of a regular dodecahedron are related to the golden ratio. A dodecahedron with an edge length of one unit has the properties:[3]
Two-dimensional symmetry projections[edit]
The regular dodecahedron has two high orthogonal projections, centered, on vertices and pentagonal faces, correspond to the A2 and H2 Coxeter planes. The edge-center projection has two orthogonal lines of reflection.
| Centered by | Vertex | Face | Edge |
|---|---|---|---|
| Image | 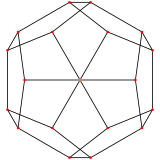
|

|

|
| Projective symmetry |
[[3]] = [6] | [[5]] = [10] | [2] |
In perspective projection, viewed on top of a pentagonal face, the regular dodecahedron can be seen as a linear-edged Schlegel diagram, or stereographic projection as a spherical polyhedron. These projections are also used in showing the four-dimensional 120-cell, a regular 4-dimensional polytope, constructed from 120 dodecahedra, projecting it down to 3-dimensions.
| Projection | Orthogonal projection | Perspective projection | |
|---|---|---|---|
| Schlegel diagram | Stereographic projection | ||
| Regular dodecahedron | 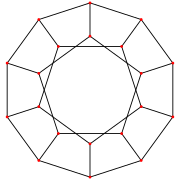
|
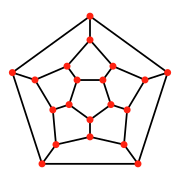
|

|
| Dodecaplex (120-cell) |

|

|

|
Spherical tiling[edit]
The regular dodecahedron can also be represented as a spherical tiling.

|

|
| Orthographic projection | Stereographic projection |
|---|
Cartesian coordinates[edit]
| Vertex coordinates: | |
| The orange vertices lie at (±1, ±1, ±1) and form a cube (dotted lines). | |
| The green vertices lie at (0, ±ϕ, ±1/ϕ) and form a rectangle on the yz-plane. | |
| The blue vertices lie at (±1/ϕ, 0, ±ϕ) and form a rectangle on the xz-plane. | |
| The pink vertices lie at (±ϕ, ±1/ϕ, 0) and form a rectangle on the xy-plane. | |
| The distance between adjacent vertices is 2/ϕ, and the distance from the origin to any vertex is √3. ϕ = 1 + √5/2 is the golden ratio. |
The following Cartesian coordinates define the 20 vertices of a regular dodecahedron centered at the origin and suitably scaled and oriented:[4]
- (±1, ±1, ±1)
- (0, ±ϕ, ±1/ϕ)
- (±1/ϕ, 0, ±ϕ)
- (±ϕ, ±1/ϕ, 0)
where ϕ = 1 + √5/2 is the golden ratio (also written τ) ≈ 1.618. The edge length is 2/ϕ = √5 − 1. The circumradius is √3.
Facet-defining equations[edit]
Similar to the symmetry of the vertex coordinates, the equations of the twelve facets of the regular dodecahedron also display symmetry in their coefficients:
- x ± ϕy = ±ϕ2
- y ± ϕz = ±ϕ2
- z ± ϕx = ±ϕ2
Properties[edit]
- The dihedral angle of a regular dodecahedron is 2 arctan(ϕ) or approximately 116.565° (where again ϕ = 1 + √5/2, the golden ratio). OEIS: A137218 Note that the tangent of the dihedral angle is exactly −2.
- If the original regular dodecahedron has edge length 1, its dual icosahedron has edge length ϕ.
- If the five Platonic solids are built with same volume, the regular dodecahedron has the shortest edges.
- It has 43,380 nets.
- The map-coloring number of a regular dodecahedron’s faces is 4.
- The distance between the vertices on the same face not connected by an edge is ϕ times the edge length.
- If two edges share a common vertex, then the midpoints of those edges form a 36-72-72 golden triangle with the body center.
As a configuration[edit]
This configuration matrix represents the dodecahedron. The rows and columns correspond to vertices, edges, and faces. The diagonal numbers say how many of each element occur in the whole dodecahedron. The nondiagonal numbers say how many of the column’s element occur in or at the row’s element.[5][6]

Here is the configuration expanded with k-face elements and k-figures. The diagonal element counts are the ratio of the full Coxeter group H3, order 120, divided by the order of the subgroup with mirror removal.
| H3 | k-face | fk | f0 | f1 | f2 | k-fig | Notes | |
|---|---|---|---|---|---|---|---|---|
| A2 | ( ) | f0 | 20 | 3 | 3 | {3} | H3/A2 = 120/6 = 20 | |
| A1A1 | { } | f1 | 2 | 30 | 2 | { } | H3/A1A1 = 120/4 = 30 | |
| H2 | {5} | f2 | 5 | 5 | 12 | ( ) | H3/H2 = 120/10 = 12 |
Geometric relations[edit]
The regular dodecahedron is the third in an infinite set of truncated trapezohedra which can be constructed by truncating the two axial vertices of a pentagonal trapezohedron.
The stellations of the regular dodecahedron make up three of the four Kepler–Poinsot polyhedra.
A rectified regular dodecahedron forms an icosidodecahedron.
The regular dodecahedron has icosahedral symmetry Ih, Coxeter group [5,3], order 120, with an abstract group structure of A5 × Z2.
Relation to the regular icosahedron[edit]
The dodecahedron and icosahedron are dual polyhedra. A regular dodecahedron has 12 faces and 20 vertices, whereas a regular icosahedron has 20 faces and 12 vertices. Both have 30 edges.
When a regular dodecahedron is inscribed in a sphere, it occupies more of the sphere’s volume (66.49%) than an icosahedron inscribed in the same sphere (60.55%).
A regular dodecahedron with edge length 1 has more than three and a half times the volume of an icosahedron with the same length edges (7.663… compared with 2.181…), which ratio is approximately 3.51246117975, or in exact terms: 3/5(3ϕ + 1) or (1.8ϕ + 0.6).
Relation to the nested cube[edit]
A cube can be embedded within a regular dodecahedron, affixed to eight of its equidistant vertices, in five different positions.[7] In fact, five cubes may overlap and interlock inside the regular dodecahedron to result in the compound of five cubes.
The ratio of the edge of a regular dodecahedron to the edge of a cube embedded inside such a regular dodecahedron is 1 : ϕ, or (ϕ − 1) : 1.
The ratio of a regular dodecahedron’s volume to the volume of a cube embedded inside such a regular dodecahedron is 1 : 2/2 + ϕ, or 1 + ϕ/2 : 1, or (5 + √5) : 4.
For example, an embedded cube with a volume of 64 (and edge length of 4), will nest within a regular dodecahedron of volume 64 + 32ϕ (and edge length of 4ϕ − 4).
Thus, the difference in volume between the encompassing regular dodecahedron and the enclosed cube is always one half the volume of the cube times ϕ.
From these ratios are derived simple formulas for the volume of a regular dodecahedron with edge length a in terms of the golden mean:
- V = (aϕ)3 · 1/4(5 + √5)
- V = 1/4(14ϕ +
a3
Relation to the regular tetrahedron[edit]
Five tetrahedra inscribed in a dodecahedron. Five opposing tetrahedra (not shown) can also be inscribed.
As two opposing tetrahedra can be inscribed in a cube, and five cubes can be inscribed in a dodecahedron, ten tetrahedra in five cubes can be inscribed in a dodecahedron: two opposing sets of five, with each set covering all 20 vertices and each vertex in two tetrahedra (one from each set, but not the opposing pair).
Just as a tetrahedron can be inscribed in a cube, so a cube can be inscribed in a dodecahedron. By reciprocation, this leads to an octahedron circumscribed about an icosahedron. In fact, each of the twelve vertices of the icosahedron divides an edge of the octahedron according to the «golden section». Given the icosahedron, the circumscribed octahedron can be chosen in five ways, giving a compound of five octahedra, which comes under our definition of stellated icosahedron. (The reciprocal compound, of five cubes whose vertices belong to a dodecahedron, is a stellated triacontahedron.) Another stellated icosahedron can at once be deduced, by stellating each octahedron into a stella octangula, thus forming a compound of ten tetrahedra. Further, we can choose one tetrahedron from each stella octangula, so as to derive a compound of five tetrahedra, which still has all the rotation symmetry of the icosahedron (i.e. the icosahedral group), although it has lost the reflections. By reflecting this figure in any plane of symmetry of the icosahedron, we obtain the complementary set of five tetrahedra. These two sets of five tetrahedra are enantiomorphous, i.e. not directly congruent, but related like a pair of shoes. [Such] a figure which possesses no plane of symmetry (so that it is enantiomorphous to its mirror-image) is said to be chiral.[8]
Relation to the golden rectangle[edit]
Golden rectangles of ratio (ϕ + 1) : 1 and ϕ : 1 also fit perfectly within a regular dodecahedron.[9] In proportion to this golden rectangle, an enclosed cube’s edge is ϕ, when the long length of the rectangle is ϕ + 1 (or ϕ2) and the short length is 1 (the edge shared with the regular dodecahedron).
In addition, the center of each face of the regular dodecahedron form three intersecting golden rectangles.[10]
Relation to the 6-cube and rhombic triacontahedron[edit]
Projection of 6-demicube into regular dodecahedral envelope
It can be projected to 3D from the 6-dimensional 6-demicube using the same basis vectors that form the hull of the rhombic triacontahedron from the 6-cube. Shown here including the inner 12 vertices, which are not connected by the outer hull edges of 6D norm length √2, form a regular icosahedron.
The 3D projection basis vectors [u,v,w] used are:
- u = (1, ϕ, 0, −1, ϕ, 0)
- v = (ϕ, 0, 1, ϕ, 0, −1)
- w = (0, 1, ϕ, 0, −1, ϕ)
History and uses[edit]
Omnidirectional sound source
Regular dodecahedral objects have found some practical applications, and have also played a role in the visual arts and in philosophy.
Iamblichus states that Hippasus, a Pythagorean, perished in the sea, because he boasted that he first divulged «the sphere with the twelve pentagons.»[11] In Theaetetus, a dialogue of Plato, Plato hypothesized that the classical elements were made of the five uniform regular solids; these later became known as the platonic solids. Of the fifth Platonic solid, the dodecahedron, Plato obscurely remarked, «…the god used [it] for arranging the constellations on the whole heaven». Timaeus (c. 360 BC), as a personage of Plato’s dialogue, associates the other four platonic solids with the four classical elements, adding that there is a fifth solid pattern which, though commonly associated with the regular dodecahedron, is never directly mentioned as such; «this God used in the delineation of the universe.»[12] Aristotle also postulated that the heavens were made of a fifth element, which he called aithêr (aether in Latin, ether in American English).
Theaetetus gave a mathematical description of all five and may have been responsible for the first known proof that no other convex regular polyhedra exist.
Euclid completely mathematically described the Platonic solids in the Elements, the last book (Book XIII) of which is devoted to their properties. Propositions 13–17 in Book XIII describe the construction of the tetrahedron, octahedron, cube, icosahedron, and dodecahedron in that order. For each solid Euclid finds the ratio of the diameter of the circumscribed sphere to the edge length. In Proposition 18 he argues that there are no further convex regular polyhedra.
Regular dodecahedra have been used as dice and probably also as divinatory devices. During the Hellenistic era, small, hollow bronze Roman dodecahedra were made and have been found in various Roman ruins in Europe. Their purpose is not certain.
In 20th-century art, dodecahedra appear in the work of M. C. Escher, such as his lithographs Reptiles (1943) and Gravitation (1952). In Salvador Dalí’s painting The Sacrament of the Last Supper (1955), the room is a hollow regular dodecahedron. Gerard Caris based his entire artistic oeuvre on the regular dodecahedron and the pentagon, which is presented as a new art movement coined as Pentagonism.
A climbing wall consisting of three dodecahedral pieces
In modern role-playing games, the regular dodecahedron is often used as a twelve-sided die, one of the more common polyhedral dice.
Immersive Media Company, a former Canadian digital imaging company, made the Dodeca 2360 camera, the world’s first 360° full-motion camera which captures high-resolution video from every direction simultaneously at more than 100 million pixels per second or 30 frames per second.[promotion?] It is based on regular dodecahedron.[citation needed]
The Megaminx twisty puzzle, alongside its larger and smaller order analogues, is in the shape of a regular dodecahedron.
In the children’s novel The Phantom Tollbooth, the regular dodecahedron appears as a character in the land of Mathematics. Each of his faces wears a different expression – e.g. happy, angry, sad – which he swivels to the front as required to match his mood.
In nature and supramolecules[edit]
The fossil coccolithophore Braarudosphaera bigelowii (see figure), a unicellular coastal phytoplanktonic alga, has a calcium carbonate shell with a regular dodecahedral structure about 10 micrometers across.[13]
Some quasicrystals and cages have dodecahedral shape (see figure). Some regular crystals such as garnet and diamond are also said to exhibit «dodecahedral» habit, but this statement actually refers to the rhombic dodecahedron shape.[14] [1]
Shape of the universe[edit]
Various models have been proposed for the global geometry of the universe. In addition to the primitive geometries, these proposals include the Poincaré dodecahedral space, a positively curved space consisting of a regular dodecahedron whose opposite faces correspond (with a small twist). This was proposed by Jean-Pierre Luminet and colleagues in 2003,[15][16] and an optimal orientation on the sky for the model was estimated in 2008.[17]
In Bertrand Russell’s 1954 short story «The Mathematician’s Nightmare: The Vision of Professor Squarepunt,» the number 5 said: «I am the number of fingers on a hand. I make pentagons and pentagrams. And but for me dodecahedra could not exist; and, as everyone knows, the universe is a dodecahedron. So, but for me, there could be no universe.»
Space filling with cube and bilunabirotunda[edit]
Regular dodecahedra fill space with cubes and bilunabirotundas (Johnson solid 91), in the ratio of 1 to 1 to 3.[18][19] The dodecahedra alone make a lattice of edge-to-edge pyritohedra. The bilunabirotundas fill the rhombic gaps. Each cube meets six bilunabirotundas in three orientations.
Related polyhedra and tilings[edit]
The regular dodecahedron is topologically related to a series of tilings by vertex figure n3.
*n32 symmetry mutation of regular tilings: {n,3}
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spherical | Euclidean | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||

|

|

|

|

|

|

|

|

|

|

|

|
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞,3} | {12i,3} | {9i,3} | {6i,3} | {3i,3} |
The regular dodecahedron can be transformed by a truncation sequence into its dual, the icosahedron:
| Family of uniform icosahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [5,3], (*532) | [5,3]+, (532) | ||||||

|

|

|

|

|

|

|

|
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duals to uniform polyhedra | |||||||

|

|

|

|

|
|||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
| Uniform octahedral polyhedra | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) |
|||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||
| Duals to uniform polyhedra | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
The regular dodecahedron is a member of a sequence of otherwise non-uniform polyhedra and tilings, composed of pentagons with face configurations (V3.3.3.3.n). (For n > 6, the sequence consists of tilings of the hyperbolic plane.) These face-transitive figures have (n32) rotational symmetry.
n32 symmetry mutations of snub tilings: 3.3.3.3.n
|
||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry n32 |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| Snub figures |

|

|

|

|

|

|

|

|
| Config. | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| Gyro figures |

|

|

|

|

|

|

|

|
| Config. | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3.3.3.3.8 | V3.3.3.3.∞ |
Vertex arrangement[edit]
The regular dodecahedron shares its vertex arrangement with four nonconvex uniform polyhedra and three uniform polyhedron compounds.
Five cubes fit within, with their edges as diagonals of the regular dodecahedron’s faces, and together these make up the regular polyhedral compound of five cubes. Since two tetrahedra can fit on alternate cube vertices, five and ten tetrahedra can also fit in a regular dodecahedron.
Stellations[edit]
The 3 stellations of the regular dodecahedron are all regular (nonconvex) polyhedra: (Kepler–Poinsot polyhedra)
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| Stellation |  Regular dodecahedron |
 Small stellated dodecahedron |
 Great dodecahedron |
 Great stellated dodecahedron |
| Facet diagram | 
|

|

|

|
Dodecahedral graph[edit]
| Regular dodecahedron graph | |
|---|---|
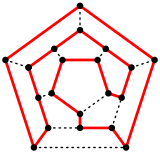
A Hamiltonian cycle in a dodecahedron. |
|
| Vertices | 20 |
| Edges | 30 |
| Radius | 5 |
| Diameter | 5 |
| Girth | 5 |
| Automorphisms | 120 (A5 × Z2)[20] |
| Chromatic number | 3 |
| Properties | Hamiltonian, regular, symmetric, distance-regular, distance-transitive, 3-vertex-connected, planar graph |
| Table of graphs and parameters |
The skeleton of the dodecahedron (the vertices and edges) form a graph. It is one of 5 Platonic graphs, each a skeleton of its Platonic solid.
This graph can also be constructed as the generalized Petersen graph G(10,2). The high degree of symmetry of the polygon is replicated in the properties of this graph, which is distance-transitive, distance-regular, and symmetric. The automorphism group has order 120. The vertices can be colored with 3 colors, as can the edges, and the diameter is 5.[21]
The dodecahedral graph is Hamiltonian – there is a cycle containing all the vertices. Indeed, this name derives from a mathematical game invented in 1857 by William Rowan Hamilton, the icosian game. The game’s object was to find a Hamiltonian cycle along the edges of a dodecahedron.

|
See also[edit]
- 120-cell, a regular polychoron (4D polytope whose surface consists of 120 dodecahedral cells)
- Braarudosphaera bigelowii − A dodecahedron shaped coccolithophore (a unicellular phytoplankton algae).
- Dodecahedrane (molecule)
- Pentakis dodecahedron
- Snub dodecahedron
- Truncated dodecahedron
References[edit]
- ^ a b Kai Wu, Jonathan Nitschke and co-workers «Systematic construction of progressively larger capsules from a fivefold linking pyrrole-based subcomponent», Nature Synthesis, 2023, DOI: https://doi.org/10.1038/s44160-023-00276-9.
- ^ Sutton, Daud (2002), Platonic & Archimedean Solids, Wooden Books, Bloomsbury Publishing USA, p. 55, ISBN 9780802713865.
- ^ Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number (First trade paperback ed.). New York City: Broadway Books. pp. 70–1. ISBN 0-7679-0816-3.
- ^ Weisstein, Eric W. «Icosahedral group». MathWorld.
- ^ Coxeter, H.S.M. (1973) [1948]. «§1.8 Configurations». Regular Polytopes (3rd ed.). New York: Dover.
- ^ Coxeter, H.S.M. (1991). Regular Complex Polytopes (2nd ed.). Cambridge: Cambridge University Press. p. 117.
- ^ http://mathworld.wolfram.com/images/eps-gif/DodecahedronCube_700.gif[bare URL image file]
- ^ Coxeter, H.S.M.; du Val, Patrick; Flather, H.T.; Petrie, J.F. (1938). The Fifty-Nine Icosahedra. Vol. 6. University of Toronto Studies (Mathematical Series). p. 4.
- ^ Knott, Ron (26 September 2016). «The Golden Geometry of Solids or Phi in 3 dimensions». Ron Knott’s Mathematics Pages. Retrieved 2022-03-19.
- ^ http://www.toshen.com/images/dodecahedronwithgoldrectang.gif[bare URL image file]
- ^ Florian Cajori, A History of Mathematics (1893)
- ^ Plato, Timaeus, Jowett translation [line 1317–8]; the Greek word translated as delineation is diazographein, painting in semblance of life.
- ^ Hagino, K., Onuma, R., Kawachi, M. and Horiguchi, T. (2013) «Discovery of an endosymbiotic nitrogen-fixing cyanobacterium UCYN-A in Braarudosphaera bigelowii (Prymnesiophyceae)». PLoS One, 8(12): e81749. doi:10.1371/journal.pone.0081749.
- ^ Dodecahedral Crystal Habit Archived 12 April 2009 at the Wayback Machine
- ^ Dumé, Belle (Oct 8, 2003). «Is The Universe A Dodecahedron?». PhysicsWorld. Archived from the original on 2012-04-25.
- ^ Luminet, Jean-Pierre; Jeff Weeks; Alain Riazuelo; Roland Lehoucq; Jean-Phillipe Uzan (2003-10-09). «Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background». Nature. 425 (6958): 593–5. arXiv:astro-ph/0310253. Bibcode:2003Natur.425..593L. doi:10.1038/nature01944. PMID 14534579. S2CID 4380713.
- ^ Roukema, Boudewijn; Zbigniew Buliński; Agnieszka Szaniewska; Nicolas E. Gaudin (2008). «A test of the Poincaré dodecahedral space topology hypothesis with the WMAP CMB data». Astronomy and Astrophysics. 482 (3): 747. arXiv:0801.0006. Bibcode:2008A&A…482..747L. doi:10.1051/0004-6361:20078777. S2CID 1616362.
- ^ «Dodecahedron and Bilunabirotunda – Wolfram Demonstrations Project».
- ^ http://www.lcv.ne.jp/~hhase/memo/m09_08b.html
- ^ Frucht, Roberto (1936–1937), «Die gruppe des Petersen’schen Graphen und der Kantensysteme der regulären Polyeder», Comment. Math. Helv., 9: 217–223, doi:10.1007/bf01258190, S2CID 121791222
- ^ Weisstein, Eric W. «Dodecahedral Graph». MathWorld.
External links[edit]
- Weisstein, Eric W. «Regular Dodecahedron». MathWorld.
- Klitzing, Richard. «3D convex uniform polyhedra o3o5x – doe».
- Editable printable net of a dodecahedron with interactive 3D view
- The Uniform Polyhedra
- Origami Polyhedra – Models made with Modular Origami
- Dodecahedron – 3-d model that works in your browser
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- VRML#Regular dodecahedron
- K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- Dodecahedron 3D Visualization
- Stella: Polyhedron Navigator: Software used to create some of the images on this page.
- How to make a dodecahedron from a Styrofoam cube
- The Greek, Indian, and Chinese Elements – Seven Element Theory
Fundamental convex regular and uniform polytopes in dimensions 2–10 |
|||||
|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn |
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon |
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | |
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell |
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | ||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | |
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | |
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | |
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | ||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | ||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope |
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds |


























 a3
a3





