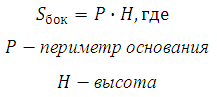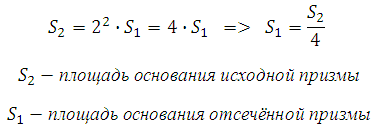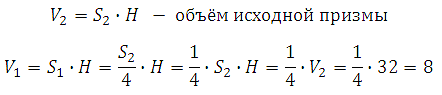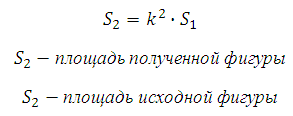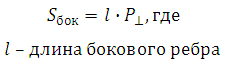Как найти площадь боковой поверхности исходной призмы - Исправление недочетов и поиск решений вместе с Examum.ru

Задача 1. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна а площадь поверхности равна

Решение: + показать

Задача 2. В правильной четырёхугольной призме известно, что Найдите угол между диагоналями и Ответ дайте в градусах.

Решение: + показать

Задача 3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и боковое ребро равно Найдите объем призмы.

Решение: + показать

Задача 4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и высота призмы равна Найдите площадь ее поверхности.

Решение: + показать

Задача 5. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и Площадь ее поверхности равна . Найдите высоту призмы.

Решение: + показать

Задача 6. Площадь поверхности правильной треугольной призмы равна Какой будет площадь поверхности призмы, если все ее ребра увеличить в два раза?

Решение: + показать

Задача 7. В правильной треугольной призме , все ребра которой равны найдите угол между прямыми и . Ответ дайте в градусах.

Решение: + показать

Задача 8. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными и и боковым ребром, равным

Решение: + показать

Задача 9. Гранью параллелепипеда является ромб со стороной и острым углом $60^{circ}.$ Одно из ребер параллелепипеда составляет с этой гранью угол в $60^{circ}$ и равно Найдите объем параллелепипеда.

Решение: + показать

Задача 10. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна а высота —

Решение: + показать

Задача 11. Найдите объем правильной шестиугольной призмы, стороны основания которой равны а боковые ребра равны

Решение: + показать

Задача 12. В правильной шестиугольной призме все ребра равны . Найдите расстояние между точками и .

Решение: + показать

Задача 13. В правильной шестиугольной призме все ребра равны Найдите угол . Ответ дайте в градусах.

Решение: + показать

Задача 14. В правильной шестиугольной призме , все ребра которой равны найдите угол между прямыми и . Ответ дайте в градусах.

Решение: + показать

Задача 15. В правильной шестиугольной призме все ребра равны Найдите тангенс угла

Решение: + показать

Задача 16. В сосуд, имеющий форму правильной треугольной призмы, налили см воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки см до отметки см. Найдите объем детали. Ответ выразите в см

Решение: + показать

Задача 17. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в раза больше, чем у первого? Ответ выразите в сантиметрах.

Решение: + показать

Задача 18. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 26, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.

Решение: + показать

Задача 19. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен Найдите объем исходной призмы.

Решение: + показать

Задача 20. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.

Задача 21. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами а боковые ребра равны и наклонены к плоскости основания под углом $30^{circ}.$

Решение: + показать

Задача 22. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно и отстоит от других боковых ребер на и Найдите площадь боковой поверхности этой призмы.

Решение: + показать

Задача 23. В правильной треугольной призме стороны оснований равны боковые рёбра равны Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер , и и точку

Решение: + показать

Задача 24. В правильной треугольной призме стороны оснований равны боковые рёбра равны Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер и

Решение: + показать

Задача 25. Объём куба равен Построено сечение проходящее через середины рёбер и и параллельное ребру Найдите объём треугольной призмы

Решение: + показать

Задача 26. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна а боковое ребро равно

Решение: + показать

Задача 27. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна а боковое ребро равно

Решение: + показать

Задача 28. Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы площадь основания которой равна а боковое ребро равно

Решение: + показать

Задача 29. Найдите объём многогранника, вершинами которого являются точки правильной шестиугольной призмы площадь основания которой равна а боковое ребро равно

Решение: + показать

Вы можете пройти тест «Призма»

Источник

Задание 8. Математика ЕГЭ. Найти площадь боковой поверхности призмы

Задание. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 79. Найдите площадь боковой поверхности исходной призмы.

Решение:

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту.

S_бок = P·h

Площадь боковой поверхности исходной треугольной призмы равна:

S₁ = P₁·h

Площадь боковой поверхности отсеченной треугольной призмы равна:

S₂ = P₂·h, по условию задачи S₂= 79.

Так как в основании треугольной призмы проведена средняя линия, то в основании получаем подобные треугольники с коэффициентом подобия 1:2. Тогда отношения периметров подобных треугольников равно:

P₂: P₁ = 1:2

P₁ = 2·P₂

S₁ = 2P₂·h = 2·S₂

S₁ = 2·79 = 158

Ответ: 158.

Источник

Версия для печати и копирования в MS Word

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 20. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 10. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 43. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 22. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 47. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 3. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 19. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 33. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 13. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 34. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 27. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 40. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 6. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 31. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 46. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 29. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 41. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 1. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 15. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 7. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 37. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 48. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 18. Найдите площадь боковой поверхности исходной призмы.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 2. Найдите площадь боковой поверхности исходной призмы.

Источник

Здравствуйте! Очередная порция задачек с призмами, рассматриваются треугольные призмы. Объединил несколько заданий схожих по одному «признаку» – у них через среднюю линию основания проходит сечение. Вопросы стоят о вычислении площади поверхности или объёма либо исходной призмы, либо отсечённой. Что важно здесь помнить?

Это свойство подобия фигур касающееся площади, в частности про треугольник уже речь была в одной из статей, посмотрите (п.2). Но даже, если вы вдруг забудете это, представленные задачи будут интуитивно понятны и решите вы их в одно действие.

77111. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 6, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.

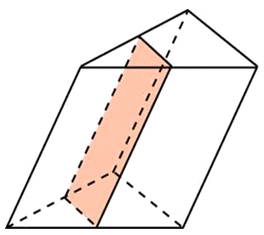
Сказано, что плоскость проходит через среднюю линию основания, то есть через точки, которые являются серединами соседних сторон треугольника. При чём она проходит параллельно боковому ребру – это означает, что указанная плоскость также проходит через середины соответствующих соседних сторон другого основания.

Без каких-либо вычислений понятно, что площадь боковой поверхности отсечённой призмы будет в два раза меньше, чем у исходной.

Посмотрите!

Высота у призм общая. Указанная плоскость разрезает две соседние боковые грани пополам.

Рассмотрим третью грань (параллельную плоскости сечения) – её площадь поверхности также в два раза меньше, так как средняя линия треугольника в два раза меньше параллельной ей стороны треугольника.

Учитывая, что высота остаётся неизменной (общая для обеих призм), можем сделать вывод, что площадь боковой поверхности (сумма площадей всех трёх граней) отсечённой призмы будет в два раза меньше.

Ответ: 3

76147. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 20. Найдите площадь боковой поверхности исходной призмы.

Задача обратная предыдущей. Формула для площади боковой поверхности призмы:

Значит для отсечённой призмы:

Высота у пирамид общая, поэтому площадь боковой поверхности исходной призмы зависит от периметра. Поскольку получившиеся треугольники в основании призмы подобны, и их соответствующие стороны относятся как 1:2, значит периметр основания исходной призмы вдвое больше периметра основания отсечённой.

А это означает, что и площадь боковой поверхности так же больше в 2 раза и равна 40.

Ответ: 40

27106. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.

Известно, что объём призмы равен произведению площади основания и высоты. Высота для указанных призм общая, значит изменение объёма зависит только от изменения площади поверхности.

Рассмотрим треугольники лежащие в основаниях призм – они подобны. Если рассматривать основание исходной призмы относительно основания отсечённой, то коэффициент подобия будет равен 2. Что это нам даёт?

Мы знаем, что пощади подобных фигур соотносятся как квадрат коэффициента подобия, значит:

Основание отсечённой призмы в 4 раза меньше.

Таким образом, и её объём будет в 4 раза меньше, то есть 8.

Формально можно расписать так:

Ответ: 8

74745. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 7. Найдите объем исходной призмы.

Задача обратная предыдущей. Объём призмы равен произведению площади основания на высоту:

Высота общая, значит объём меняется в зависимости от изменения площади основания.

Треугольник лежащий в основании исходной призмы, как уже сказано, подобен треугольнику лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию.

Площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть:

Таким образом, площадь основания исходной призмы больше площади основания отсечённой призмы в 4 раза.

Следовательно объем исходной призмы будет в 4 раза больше объема отсечённой призмы. Таким образом, искомый объём равен 28.

Ответ: 28

Ещё три задачи про площадь поверхности призмы

245356. Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза?

Увеличим все рёбра призмы в три раза. Что получается?

Получается, что каждая грань полученной призмы и соответствующая ей грань исходной призмы являются подобными фигурами. При чём коэффициент подобия равен 3. Мы, что площади подобных фигур пропорциональны квадрату коэффициента подобия, то есть:

Это означает, что площадь каждой отдельной грани нашей призмы увеличится в 9 раз. Так как площадь поверхности всей призмы это сумма площадей всех граней, то разумеется, что и вся площадь поверхности призмы также увеличится в 9 раз.

Ответ: 54

*На самом деле не важно о каком теле идёт речь (о призме, пирамиде, кубе, параллелепипеде), суть одна.

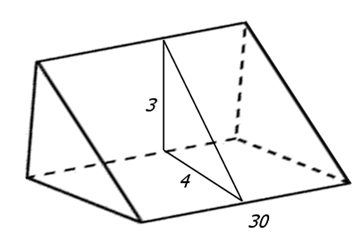
В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 30 и отстоит от других боковых ребер на 3 и 4. Найдите площадь боковой поверхности этой призмы.

На момент написания статьи эта задача из открытого банка заданий ЕГЭ удалена, но мы её рассмотрим, так вернуться может туда в любой момент, а значит и быть на экзамене в будущие годы.

Для вычисления боковой поверхности призмы воспользуемся формулой:

В данном случае боковое ребро это общее ребро перпендикулярных друг другу граней, оно равно 30. Перпендикулярным сечением призмы является прямоугольный треугольник с катетами 3 и 4. По теореме Пифагора найдём его гипотенузу и сможем вычислить периметр:

Таким образом:

Второй путь решения!

Указанная выше формула для кого-то может быть не понятна. В чём её смысл и что она выражает?

Посмотрите на каждую отдельную грань (положив призму на бок) – это параллелограммы. При чём основания этих параллелограммов равны и равны они боковому ребру, то есть 30. Высоты у них будут разные.

Две нам известны 3 и 4, третья не известна. Но её мы можем найти. Разрежем призму перпендикулярно боковым рёбрам, сечением разреза будет прямоугольный треугольник с катетами 3 и 4, найдём гипотенузу:

Получается, что площадь боковой поверхности равна сумме площадей трёх параллелограммов:

Ответ: 360

72605. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 6, а высота 2.

Призма правильная, значит гранями являются равные по площади прямоугольники. Так как призма шестиугольная, то имеем 6 таких прямоугольников. Площадь боковой поверхности равна сумме площадей всех боковых граней:

Ответ: 72

27068. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.

Посмотреть решение

27107. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

Посмотреть решение

27153. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.

Посмотреть решение

27150. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.

Посмотреть решение

27057. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота 10.

Посмотреть решение

На этом всё, всего доброго!

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

Площадь боковой грани треугольной призмы равен сумме трех прямоугольников. При отсечении от нее части плоскостью, проходящей через среднюю линию основания два из этих прямоугольников разделится пополам, что видно по рисунку. Площадь третьего прямоугольника и площадь сечения (тоже прямоугольник, на рисунке выделен цветом) также относятся как 2:1, так как средняя линия треугольника равна половине основания. Это ширина отсеченного прямоугольника, а высоты всех перечисленных прямоугольников одинаковы. Вывод: площадь боковой поверхности отсечённой треугольной призмы равен половине площади боковой поверхности исходной призмы, то есть 24/2=12. Ответ: 12.

Знаете ответ?

Смотрите также:

ЕГЭ Базовая математика, Как решить задачу про монеты в обменнике?

ЕГЭ Базовая математика, Как решить задачу про насосы?

ЕГЭ Базовая математика, Как решить задачу про квартиру Саши?

ЕГЭ Базовая математика, Как найти корень уравнения с логарифмом log0.2?

ЕГЭ Базовая математика, Как определить объём нового конуса?

Какие итоги ЕГЭ-2022 по математике, какой средний балл?

Какие задания, решение и ответы по математике ЕГЭ 2022?

ЕГЭ Базмат, Как правильно решить пример на разность квадратов?

ЕГЭ Базмат, Как правильно решить задачу про квартиру с комнатами?

ЕГЭ Базмат, Как определить градусную меру угла в задаче с диаметром?

Источник