В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.
Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.
-
Формула площади правильной пирамиды
- 1. Общая формула
- 2. Площадь правильной треугольной пирамиды
- 3. Площадь правильной четырехугольной пирамиды
- 4. Площадь правильной шестиугольной пирамиды
Формула площади правильной пирамиды
1. Общая формула
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.
Sполн. = Sбок. + Sосн.
Боковой гранью правильной пирамиды является равнобедренный треугольник.
Площадь треугольника вычисляется по формулам:
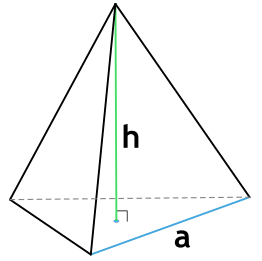
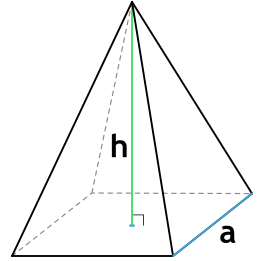
1. Через длину основания (a) и высоту (h):
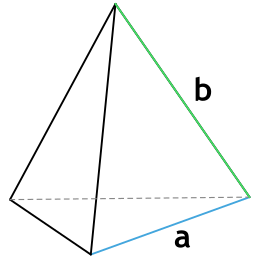
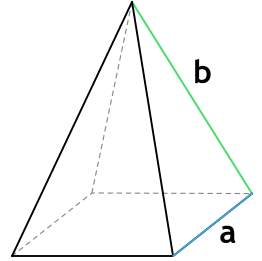
2. Через основание (a) и боковую сторону (b):
Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.
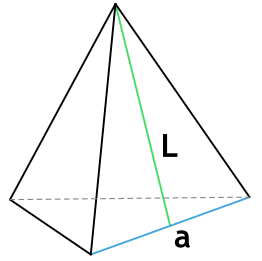
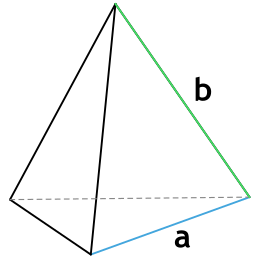
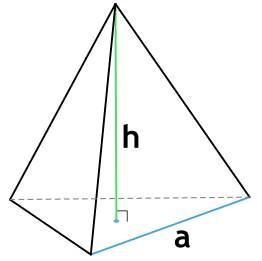
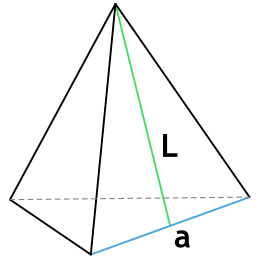
2. Площадь правильной треугольной пирамиды
Основание: равносторонний треугольник.
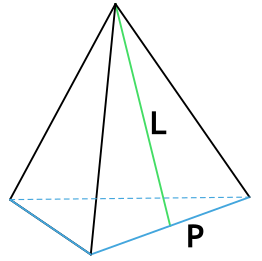
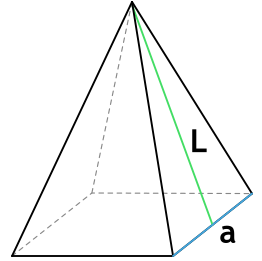
L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.
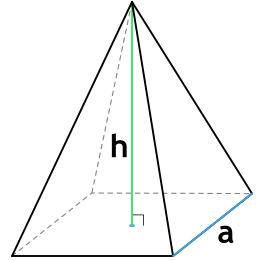
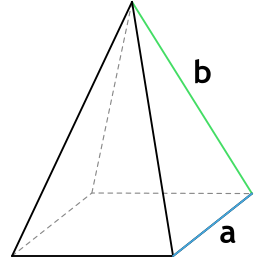
3. Площадь правильной четырехугольной пирамиды
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 2aL |
 |
|
| полная | Sполн. = a2 + 2aL |
 |
microexcel.ru
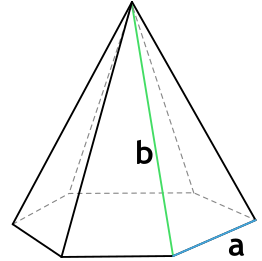
4. Площадь правильной шестиугольной пирамиды
Основание: правильный шестиугольник
Полная площадь боковой поверхности пирамиды состоит из суммы площадей его боковых граней.
В четырехугольной пирамиде различается два вида граней – четырехугольник в основании и треугольники с общей вершиной, которой образуют боковую поверхность.
Для начала потребуется рассчитать площадь боковых граней. Для этого можно использовать формулы площади треугольника, а можно также воспользоваться формулой площади поверхности четырехугольной пирамиды (только в случае, если многогранник правильный). Если пирамида правильная и в ней известна длина ребра a основания и проведенной к нему апофемы h, то:
Если по условиям даны длина ребра c правильной пирамиды и длина стороны основания a, то можно найти значение по следующей формуле:
Если же дана длина ребра в основании и противолежащий ей острый угол у вершины, то можно рассчитать площадь боковой поверхности по соотношению квадрата стороны a к удвоенному косинусу половины угла α:
Рассмотрим пример расчета площади поверхности четырехугольной пирамиды через боковое ребро и сторону основания.
Задача: пусть дана правильная четырехугольная пирамида. Длина ребра b = 7 см, длина стороны основания a = 4 см. Подставим заданные значения в формулу:
Мы показали расчеты площади одной боковой грани для правильной пирамиды. Соответственно. Чтобы найти площадь всей поверхности необходимо умножить результат на количество граней, то есть на 4. Если пирамида произвольная и ее грани не равны между собой, то рассчитать площадь необходимо для каждой отдельной стороны. Если в основании лежит прямоугольник или параллелограмм, то стоит вспомнить их свойства. Стороны у этих фигур попарно параллельны, а соответственно грани пирамиды будут также попарно одинаковы.
Формула площади основания четырехугольной пирамиды напрямую зависит от того, какой четырехугольник лежит в основании. Если пирамида правильная, то площадь основания рассчитывается по формуле площади квадрата, если в основании лежит ромб, то потребуется вспомнить, как находится площадь ромба. Ели же в основании лежит прямоугольник, то найти его площадь будет довольно просто. Достаточно знать длины сторон основания. Рассмотрим пример расчета площади основания четырехугольной пирамиды.
Задача: Пусть дана пирамида, в основании которой лежит прямоугольник со сторонами a = 3 см, b = 5 см. К каждой из сторон из вершины пирамиды опущена апофема. h-a=4 см,h-b=6 см. Вершина пирамиды лежит на одной линии с точкой пересечения диагоналей. Найдите полную площадь пирамиды.
Формула площади четырехугольной пирамиды состоит из суммы площадей всех граней и площади основания. Для начала найдем площадь основания:
Теперь рассмотрим грани пирамиды. Они попарно одинаковы, потому что высота пирамиды пересекает точку пересечения диагоналей. То есть, в нашей пирамиде есть два треугольника с основанием a и высотой h-a, а также два треугольника с основанием b и высотой h-b. Теперь найдем площадь треугольника по известной формуле:
Теперь выполним пример расчета площади четырехугольной пирамиды. В нашей пирамиде с прямоугольником в основании, формула будет выглядеть так:
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Формула для вычисления площади боковой поверхности правильной чутырехугольной пирамиды
Через сторону и боковую грань $S=2 a sqrt{b^{2}-frac{a^{2}}{4}}$, где:
a — сторона основания
b — боковая грань
Через стороны и высоту $S=frac{4 cdot a}{2} sqrt{h^{2}+left(frac{a}{2 cdot operatorname{tg}left(45^{circ}right)}right)^{2}}$, где:
a — сторона основания
h — высота

{S_{полн} = dfrac{1}{2}PL + S}
На странице вы найдете онлайн-калькуляторы, которые помогут найти площадь полной и боковой поверхности правильной пирамиды, а также треугольной, четырехугольной и шестиугольной пирамиды. Кроме того приводятся формулы, по которым вы можете произвести расчет самостоятельно.
- калькулятор площади поверхности пирамиды
- формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
- формула площади полной поверхности правильной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и боковую грань
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной пирамиды через периметр и апофему
- формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- примеры задач
Познакомьтесь с важными понятиями, которые необходимо знать для расчета площади поверхности пирамиды.
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.
Площадь полной поверхности пирамиды — это сумма площадей боковых граней и площади основания.
Площадь боковой поверхности пирамиды — это совокупная площадь всех боковых граней пирамиды.
Апофема — перпендикуляр, опущенный из вершины пирамиды на ребро основания.
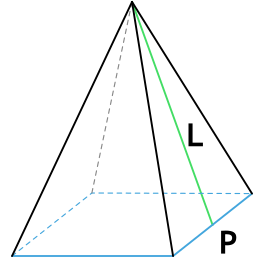
Формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
{S_{полн} = dfrac{1}{2}PL+S}
P — периметр основания пирамиды
L — апофема пирамиды
S — площадь основания пирамиды
Формула площади полной поверхности правильной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{na}{2} {Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} + sqrt{h^2+ Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
n — число сторон основания
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{a^2 sqrt{3}+6aL}{4}}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{a^2 sqrt{3}+6a sqrt{b^2 — dfrac{a^2}{4}}}{4}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{3a}{2} {Bigg( dfrac{a}{2 tg ( 60°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{полн} = 2a {Bigg( dfrac{a}{2 tg ( 45°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{полн} = a^2+2aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3asqrt{b^2-dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{полн} = 3a {Bigg( dfrac{a}{2 tg ( 30°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2} Bigg)}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной пирамиды через периметр и апофему
{S_{бок} = dfrac{1}{2}PL}
P — периметр основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{na}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( dfrac{180°}{n})} Bigg) ^2} }
a — сторона основания пирамиды
h — высота пирамиды
n — число сторон основания
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{бок} = dfrac{3}{2}aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{бок} = dfrac{3a sqrt{b^2 — dfrac{a^2}{4}}}{2}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{3a}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
{S_{бок} =dfrac{1}{2}PL}
P — периметр основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{бок} = 2aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 2a sqrt{b^2 — dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{бок} = 3aL}
a — сторона основания пирамиды
L — апофема пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 3asqrt{b^2-dfrac{a^2}{4}}}
a — сторона основания пирамиды
b — боковая грань пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{бок} = 3a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2}}
a — сторона основания пирамиды
h — высота пирамиды
Примеры задач на нахождение площади поверхности пирамиды
Задача 1
Стороны основания правильной четырехугольной пирамиды равны 60см, боковые ребра равны 78см. Найдите площадь поверхности этой пирамиды.
Решение
Так как пирамида правильная четырехугольная, то воспользуемся соответствующей формулой площади поверхности через сторону основания и боковую грань.
S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}} = 60^2 + 2 cdot 60 sqrt{78^2- dfrac{60^2}{4}} = 3600 + 120 sqrt{6084- dfrac{3600}{4}} = 3600 + 120 sqrt{6084 — 900} = 3600 + 120 sqrt{5184} = 3600 + 120 cdot 72 = 3600 + 8640 = 12240 : см²
Ответ: 12240 см²
Проверим полученный ответ с помощью калькулятора .
Задача 2
Найти площадь боковой поверхности правильной треугольной пирамиды со стороной 6см и апофемой 10см.
Решение
Из условия мы знаем апофему и сторону правильной треугольной пирамиды, поэтому нам потребуется эта формула.
S_{бок} = dfrac{3}{2}aL = dfrac{3}{2} cdot 6 cdot 10 = dfrac{3}{2} cdot 60 = 90 : см²
Ответ: 90 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найти площадь боковой поверхности правильной четырехугольной пирамиды сторона основания 6см и высота 4см.
Решение
Подставим значения в формулу и произведем расчет.
S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} = 2 cdot 6 sqrt{4^2+ Bigg( dfrac{6}{2 tg ( 45°)} Bigg) ^2} = 60 : см²
Ответ: 60 см²
Проверка .
Типичными геометрическими задачами на плоскости и в трехмерном пространстве являются проблемы определения площадей поверхностей разных фигур. В данной статье приведем формулу площади боковой поверхности правильной пирамиды четырехугольной.
Что собой представляет пирамида?
Приведем строгое геометрическое определение пирамиды. Предположим, что имеется некоторый многоугольник с n сторонами и с n углами. Выберем произвольную точку пространства, которая не будет находиться в плоскости указанного n-угольника, и соединим ее с каждой вершиной многоугольника. Мы получим фигуру, имеющую некоторый объем, которая называется n-угольной пирамидой. Для примера покажем на рисунке ниже, как выглядит пятиугольная пирамида.
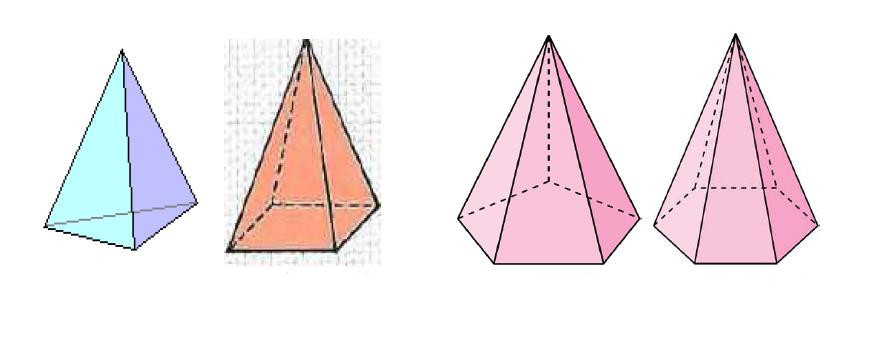
Два важных элемента любой пирамиды — это ее основание (n-угольник) и вершина. Эти элементы соединены друг с другом n треугольниками, которые в общем случае не равны друг другу. Перпендикуляр, опущенный из вершины к основанию, называется высотой фигуры. Если он пересекает основание в геометрическом центре (совпадает с центром масс многоугольника), то такую пирамиду называют прямой. Если помимо этого условия основание является правильным многоугольником, то и вся пирамида называется правильной. Рисунок ниже показывает, как выглядят правильные пирамиды с треугольным, четырехугольным, пятиугольным и шестиугольным основаниями.
Поверхность пирамиды
Прежде чем переходить к вопросу о площади боковой поверхности правильной пирамиды четырехугольной, следует подробнее остановиться на понятии самой поверхности.
Как было сказано выше и показано на рисунках, любая пирамида образована набором граней или сторон. Одна сторона является основанием, и n сторон представляют собой треугольники. Поверхность всей фигуры — это сумма площадей каждой ее стороны.
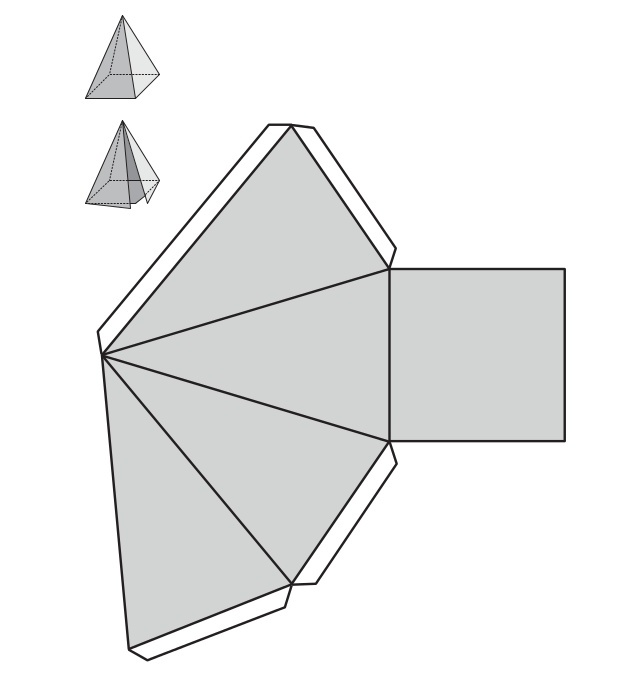
Поверхность удобно изучать на примере развертки фигуры. Развертка для правильной четырехугольной пирамиды приведена на рисунки ниже.
Видим, что площадь ее поверхности равна сумме четырех площадей одинаковых равнобедренных треугольников и площади квадрата.
Общую площадь всех треугольников, которые образуют боковые стороны фигуры, принято называть площадью боковой поверхности. Далее покажем, как ее рассчитать для четырехугольной пирамиды правильной.
Площадь боковой поверхности четырехугольной правильной пирамиды
Чтобы вычислить площадь боковой поверхности указанной фигуры, снова обратимся к приведенной выше развертке. Предположим, что нам известна сторона квадратного основания. Обозначим ее символом a. Видно, что каждый из четырех одинаковых треугольников, имеет основание длиной a. Чтобы вычислить их суммарную площадь, необходимо знать эту величину для одного треугольника. Из курса геометрии известно, что треугольника площадь St равна произведению основания на высоту, которое следует поделить пополам. То есть:
St = 1/2*hb*a.
Где hb — высота равнобедренного треугольника, проведенная к основанию a. Для пирамиды эта высота является апотемой. Теперь остается умножить полученное выражение на 4, чтобы получить площадь Sb поверхности боковой для рассматриваемой пирамиды:
Sb = 4*St = 2*hb*a.
Эта формула содержит два параметра: апотему и сторону основания. Если последняя в большинстве условий задач известна, то первую приходится вычислять, зная другие величины. Приведем формулы для расчета апотемы hb для двух случаев:
- когда известна длина бокового ребра;
- когда известна высота пирамиды.
Если обозначить длину ребра бокового (сторона равнобедренного треугольника) символом L, тогда апотема hb определиться по формуле:
hb = √(L2 — a2/4).
Это выражения является результатом применения теоремы Пифагора для треугольника боковой поверхности.
Если известна высота h пирамиды, тогда апотему hb можно рассчитать так:
hb = √(h2 + a2/4).
Получить это выражение также не сложно, если рассмотреть внутри пирамиды прямоугольный треугольник, образованный катетами h и a/2 и гипотенузой hb.
Покажем, как применять эти формулы, решив две интересные задачи.
Задача с известной площадью поверхности
Известно, что площадь боковой поверхности четырехугольной пирамиды правильной равна 108 см2. Необходимо вычислить значение длины ее апотемы hb, если высота пирамиды равна 7 см.
Запишем формулу площади Sb поверхности боковой через высоту. Имеем:
Sb = 2*√(h2 + a2/4) *a.
Здесь мы просто подставили соответствующую формулу апотемы в выражение для Sb. Возведем обе части равенства в квадрат:
Sb2 = 4*a2*h2 + a4.
Чтобы найти значение a, сделаем замену переменных:
a2 = t;
t2 + 4*h2*t — Sb2 = 0.
Подставляем теперь известные значения и решаем квадратное уравнение:
t2 + 196*t — 11664 = 0.
t ≈ 47,8355.
Мы выписали только положительный корень этого уравнения. Тогда стороны основания пирамиды будет равна:
a = √t = √47,8355 ≈ 6,916 см.
Чтобы получить длину апотемы, достаточно воспользоваться формулой:
hb = √(h2 + a2/4) = √(72 + 6,9162/4) ≈ 7,808 см.
Боковая поверхность пирамиды Хеопса
Определим значение площади поверхности боковой для самой большой египетской пирамиды. Известно, что в ее основании лежит квадрат с длиной стороны 230,363 метра. Высота сооружения изначально составляла 146,5 метра. Подставим эти цифры в соответствующую формулу для Sb, получим:
Sb = 2*√(h2 + a2/4) *a = 2*√(146,52+230,3632/4)*230,363 ≈ 85860 м2.
Найденное значение немного больше площади 17 футбольных полей.