Как найти площадь боковых граней прямоугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Площадь поверхности прямоугольного параллелепипеда

4.6

Средняя оценка: 4.6

Всего получено оценок: 495.

4.6

Средняя оценка: 4.6

Всего получено оценок: 495.

В 5 классе в курсе математики изучается тема прямоугольного параллелепипеда. Сегодня мы поговорим о формулах для нахождения площади боковой поверхности и площади полной поверхности этой фигуры, которые наиболее часто вызывают затруднения у учеников.

Материал подготовлен совместно с учителем первой категории Камушковой Натальей Владимировной.

Опыт работы учителем математики — 27 лет.

Определения

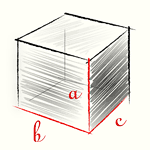
Параллелепипед – это фигура в пространстве, которая состоит из шести четырехугольников.

Каждый четырехугольник – это грань параллелепипеда. Среди граней различают четыре боковые и два основания. Если в основании фигуры находится прямоугольник, то многогранник называется прямоугольным параллелепипедом.

Стороны граней – это ребра. У параллелепипеда всего 12 ребер.

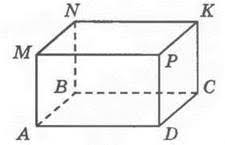
Параллелепипед имеет 8 вершин, для их обозначения используют заглавные латинские буквы.

Если две грани не имеют общего ребра, то они называются противоположными. Так как каждая грань прямоугольного параллелепипеда – это прямоугольник, у которого противоположные стороны равны, то и противоположные грани прямоугольного параллелепипеда также равны.

Длина ребер определяет основные характеристики прямоугольного параллелепипеда: площадь, периметр, объем.

Рис. 1. Прямоугольный параллелепипед

Примеры таких фигур мы часто встречаем в нашей жизни: кирпич, коробка, системный блок компьютера.

Математическая фигура – прямоугольный параллелепипед активно используется в искусстве, архитектуре и прочих областях.

Различают несколько видов параллелепипедов, с основанием в виде квадрата, параллелограмма или прямоугольника.

Формула для нахождения площади

Для того, чтобы найти площадь боковой поверхности прямоугольного параллелепипеда, необходимо вычислить по отдельности площадь каждой боковой грани, а затем просуммировать получившиеся значения.

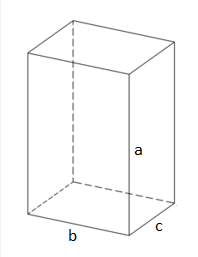
$S = ab$;

$S = ac$; где a, b, c – стороны фигуры.

Рис. 2. Прямоугольный параллелепипед

А так как противоположные грани равны, то есть $AMPD = BNKC$, $AMNB = DPKC$, их сумма и будет площадью боковой поверхности многоугольника.

$S= 2(ab + ac)$

Соответственно, чтобы вычислить площадь полной поверхности прямоугольного параллелепипеда необходимо сложить площадь боковой поверхности и две площади основания. В итоге получится формула площади прямоугольного параллелепипеда.

$S = 2(ab + ac) + 2 bc = 2(ab + ac + bc)$

Иногда для уточнения возле знака площади пишут краткое обозначение например, S п.п. – площадь полной поверхности, либо S б.п. – площадь боковой поверхности. Это помогает во время выполнения задания не перепутать нужные данные.

Пример задания

Найти площадь полной поверхности прямоугольного параллелепипеда, если длина и ширина основания 4 см и 3 см соответственно, а высота равна 2 см.

Рис. 3. Прямоугольный параллелепипед со сторонами a, b, c

Решение:

S п.п. = 2(ab + ac + bc)

S п.п. = 2(4*3 + 4*2 + 3*2) = 52 см²

Таким образом, S п.п. = 52 см².

Для площади поверхности прямоугольного параллелепипеда используют те же единицы измерения, в которых были приведены длины ребер. Если длины ребер прямоугольного параллелепипеда даны в разных единицах измерения, то их нужно перевести в одинаковые.

Что мы узнали?

Мы познакомились с элементами прямоугольного параллелепипеда: грани, ребра, основание. А также ознакомились с формулами для нахождения площади его боковой и полной поверхности, которые можно использовать для решения заданий.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Марина Яговцева

8/10
Розочка Ангелиночка

10/10
Слава Сироткин

10/10
Тома Зимина

7/10
Artem Sevastanov

10/10
Влад Чибиряев

10/10
Александр Селезнев

10/10
Акрам Сафарбеков

10/10
Вера Машковцева

10/10
Александр Семёнов

9/10

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 495.

А какая ваша оценка?

Источник

Площадь поверхности параллелепипеда

Содержание:

Что такое площадь поверхности параллелепипеда
Формула нахождения полной площади
Вычисление площади боковой поверхности прямоугольного параллелепипеда
Примеры решения задач

Что такое площадь поверхности параллелепипеда

Определение

Параллелепипед — четырехугольная призма, основаниями которой являются параллелограммы. Частный случай этой геометрической фигуры — прямой параллелепипед, у которого все грани являются прямоугольниками.

В общем случае площадь — это численное значение, характеризующее размер двумерной геометрической фигуры.

Параллелепипед может существовать только в трех измерениях, поэтому для него вводится понятие площади поверхности. В геометрическом смысле площадь поверхности объемной фигуры является совокупностью площадей ее граней.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Формула нахождения полной площади

В задачах чаще всего имеется дело с прямоугольным параллелепипедом. Для него полная площадь поверхности вычисляется следующим образом:

(S=2cdot(acdot b+acdot c+bcdot c))

где a, b и c — длины ребер, исходящих из любой вершины параллелепипеда.

Рассмотрим то, как данная формула выводится. Как уже упоминалось выше, площадь поверхности объемной фигуры является совокупностью площадей ее граней. Для наглядности возьмем параллелепипед ABCDA₁B₁C₁D₁.

Параллелепипед

Рисунок 1

Полная площадь его поверхности равняется сумме площадей всех граней: (S_{пар}=S_{AA_1D_1D}+S_{DD_1C_1C}+S_{CC_1B_1B}+S_{BB_1A_1A}+S_{ABCD}+S_{A_1B_1C_1D_1})

Согласно свойствам параллелепипеда, его противоположные грани равны между собой. Следовательно, нет необходимости вычислять площадь всех шести граней, можно ограничиться тремя, а затем их сумму умножить на 2:

(S_{пар}=2cdotleft(S_{AA_1D_1D}+S_{BB_1A_1A}+S_{ABCD}right))

Грани прямого параллелепипеда являются прямоугольниками. Площадь данной фигуры равняется произведению ее сторон:

(S_▭=acdot b)

У выбранных нами для расчета площади граней есть три общие стороны: AB, AD и AA₁. Для удобства обозначим их как a, b и c соответственно.

Параллелепипед 2

Рисунок 2

Таким образом:

(S_{ABCD}=acdot b)

(S_{AA_1D_1D}=acdot c)

(S_{BB_1A_1A}=bcdot c)

Подставим данные значения в обозначенную выше формулу площади параллелепипеда:

(S_{пар}=2cdotleft(acdot b+acdot c+bcdot cright))

Вычисление площади боковой поверхности прямоугольного параллелепипеда

Кроме полной площади поверхности, в расчетах иногда необходимо вычислить площадь боковой поверхности, то есть совокупность площадей боковых граней, без учета оснований.

Для этого есть три взаимосвязанные формулы:

(S_{бок}=P_{осн}cdot h,) где (P_{осн}) — периметр основания параллелепипеда; h — высота. На рисунке выше она равняется стороне, обозначенной как c.
(S_{бок}=2cdot acdot c+2cdot bcdot c), где a, b и c — длины ребер, исходящих из любой вершины параллелепипеда.
(S_{бок}=2cdot ccdot(a+b).)

Примеры решения задач

Задача

Вычислить полную площадь поверхности прямоугольного параллелепипеда ABCDA₁B₁C₁D₁.

Диагональ

Рисунок 3

Дано: AB = 3, A₁B = 6, AD = 5.

Решение

Для расчета полной площади необходимо знать длины трех сторон. В данном случае нам понадобится вычислить длину стороны AA₁. Так как длина диагонали A₁B известна, сделать это нетрудно.

Воспользуемся теоремой Пифагора:

(A_1B=sqrt{{AA_1}^2+{AB}^2})

Соответственно, ({AA_1}=sqrt{{A_1B}^2-{AB}^2}=sqrt{6^2-3^2}=sqrt{36-9}=sqrt{25}=5)

Подставим известные значения в формулу расчета площади поверхности:

(S=2cdot(acdot b+acdot c+bcdot c))

(S=2cdot(ABcdot AD+ABcdot AA_1+ADcdot AA_1)=2cdot(3cdot5+3cdot5+5cdot5)=2cdot(15+15+25)=2cdot55=110)

Ответ: S=110.

Задача 2

Вычислить длину стороны прямого параллелепипеда ABCDA₁B₁C₁D₁.

Задача 2

Рисунок 4

Дано: S_пов=96, S_бок=60, b=6.

Решение

Так как нам известна одна из сторон основания — b а в основании параллелепипеда лежит прямоугольник, найти вторую сторону проще всего будет через площадь этого основания:

(S=acdot b)

Отличие площади боковой поверхности от полной в том, что в ней не учитываются нижняя и верхняя грани фигуры. Следовательно, их разность будет равняться двум площадям основания. Вычислим это значение:

(S_{пов}-S_{бок}=2cdot acdot b+2cdot acdot c+2cdot bcdot c-2cdot acdot c-2cdot bcdot c=2cdot acdot b)

Преобразуем выражение так, чтобы вычислить длину неизвестной стороны:

(2cdot acdot b=S_{пов}-S_{бок})

(a=frac{S_{пов}-S_{бок}}{2cdot b}=frac{96-60}{2cdot6}=frac{36}{12}=3)

Ответ: a=3.

Насколько полезной была для вас статья?

Рейтинг: 4.00 (Голосов: 7)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Формулы объёма и площади поверхности. Многогранники.

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Куб		диагональ
Параллелепипед	$V=S_text{OCH}h, h -$ высота
Прямоугольный параллелепипед		$d=sqrt{a^2+b^2+c^2}$
Призма	$V=S_text{OCH}h$	$S = 2S_text{OCH}+$
Пирамида	$V=frac{1}{3}S_text{OCH}h$	$S = S_text{OCH}+$

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Решение:

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб

Очевидно, их 6, поскольку у куба 6 граней.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Разберем задачи, где требуется найти площадь поверхности многогранника.

Мы рассмотрим призмы и пирамиды. Начнем с призмы.

Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.

Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.

Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Многогранник на рисунке – это прямая призма с высотой 12.

$P_text{OCH}=8+6+6+2+2+4=28.$

Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:

(больший квадрат), (маленький прямоугольник), $S_text{OCH}=36+8=44$

Подставим все данные в формулу: и найдем площадь поверхности многогранника:

Ответ: 424.

Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Решение.

Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:

$P_text{OCH}=4+5+2+1+2+4=18.$

Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:

(большой прямоугольник), $S_text{OCH}=16+2=18$ (маленький прямоугольник).

Найдем площадь полной поверхности:

Ответ: 54

Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Покажем еще один способ решения задачи.

Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.

И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:

Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.

Ответ: 42

Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.

Решение.

Пусть АВ = 5 см, ВС = 3 см, тогда $angle{ABC}=120^{circ}$

Из по теореме косинусов найдем ребро АС:

$AC^2=AB^2+BC^2-2cdot ABcdot BC cdot cos120^{circ}$

$AC^2=25+9-2cdot5cdot3cdotleft(-frac{1}{2}right)=47, ~AC = 7$

Отрезок АС – большая сторона , следовательно, большая боковая грань призмы.

Поэтому или откуда h=5.

Ответ: 75

Теперь две задачи на площадь боковой поверхности пирамиды.

Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.

Решение.

Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.

Проведем , тогда (по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.

– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.

Из прямоугольного получим:

$AK=sqrt{AB^2-BK^2}=sqrt{13^2-5^2}=sqrt{169-25}=sqrt{144}=12.$

Из прямоугольного имеем:

$DK=sqrt{DA^2+AK^2}=sqrt{9^2+12^2}=sqrt{81+144}=sqrt{225}=15.$

(по двум катетам), тогда $S_{ADB}=S_{ADC},$ следовательно

$=2S_{ADB}+S_{BDC},$ $=2cdotfrac{1}{2}cdot13cdot9+frac{1}{2}cdot10cdot15=117+75=192.$

Ответ: 192

Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.

Решение:

Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.

Площадь поверхности пирамиды равна

где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.

Значит, полупериметр основания .

Апофему найдем по теореме Пифагора:

$h=sqrt{37^2-12^2}=sqrt{(37-12)(37+12)}=sqrt{25cdot49}=5cdot7=35$

Ответ: 2256

Как решать задачи на нахождение объема многогранника сложной формы?

Покажем два способа.

Первый способ

1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.

Второй способ.

1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.

Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

1) Достроим составной многогранник до параллелепипеда.

2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:

3) Найдем объем лишней части, то есть маленького параллелепипеда.

Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем

4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:

Ответ: 220.

Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.

Объем призмы равен $V=S_{OCH}cdot h$ , а так как призма прямая, то ее боковое ребро является и высотой, то есть h=6.

Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания

$S_{OCH}=frac{1}{2}cdot ab=frac{1}{2}cdot6cdot7=21.$

Ответ: 126

Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.

Решение.

Объем призмы равен $V = S_{OCH}cdot h$

Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.

Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.

Объем воды не изменился, Так как высота воды h_2 должна быть в 81 раз меньше, чем h_1. Она равна (см).

Ответ: 4

Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды ABDA_1.

Решение.
Опустим из вершины A_1 высоту A_1H Н на основание ABCD.

$=S_{ABCD}cdot A_1H$

$=frac{1}{3}S_{ABD}cdot A_1H$

Диагональ основания делит его на два равных треугольника, следовательно, $S_{ABD}=frac{1}{2}S_{ABCD}.$

Имеем:

$ABDA_1=frac{1}{3}S_{ABD}cdot A_1H=frac{1}{3}cdotfrac{1}{2}S_{ABCD}cdot A_1H=frac{1}{6}V_{ABCDA_1B_1C_1D_1}=frac{1}{6}cdot21=3,5.$

Ответ: 3,5

Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна

Решение.
По формуле объема пирамиды, .

В основании пирамиды лежит правильный треугольник. Его площадь равна $S_{OCH}=frac{a^2sqrt{3}}{4}.$

$S_{OCH}=frac{8^2sqrt{3}}{4}=frac{64sqrt{3}}{4}=16sqrt{3}.$

Объем пирамиды $V=frac{1}{3}cdot16sqrt{3}cdot6sqrt{3}=16cdot6=96.$

Ответ: 96

Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.

Решение.

По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.

Пусть AD=x, тогда $S_{OCH}=x^2.$

Так как точки М и К – середины АD и DС соответственно, то $DM=DK=frac{x}{2}.$

$S_{MDK}=frac{1}{2}MDcdot DK=frac{1}{2}cdotfrac{x}{2}cdotfrac{x}{2}=frac{1}{8}x^2.$

Площадь треугольника MDK, лежащего в основании новой призмы, составляет $frac{1}{8}$ часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: $V=S_{OCH}cdot h$ , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен 32:8=4.

Ответ: 4

Докажем полезную теорему.

Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.

Доказательство:

Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.

$S=P_{perp}cdot l.$

Больше задач на формулы объема и площади поверхности здесь.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

{S_{полн} = 2(ab+bc+ac)}

Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер — это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.

В дополнение на сайте можно найти объем параллелепипеда.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.

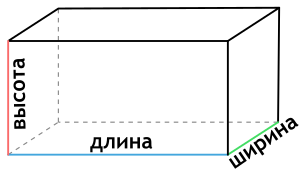
Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота — это ребра прямоугольного параллелепипеда.

Содержание:

калькулятор площади поверхности прямоугольного параллелепипеда
формула площади поверхности прямоугольного параллелепипеда
формула площади боковой поверхности прямоугольного параллелепипеда
примеры задач

Формула площади поверхности прямоугольного параллелепипеда

{S_{полн} = 2(ab+bc+ac)}

a — длина прямоугольного параллелепипеда

b — ширина прямоугольного параллелепипеда

c — высота прямоугольного параллелепипеда

Формула площади боковой поверхности прямоугольного параллелепипеда

{S_{бок} = 2(ac+bc)}

a — длина прямоугольного параллелепипеда

b — ширина прямоугольного параллелепипеда

c — высота прямоугольного параллелепипеда

Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда

Задача 1

Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.

Решение

Для нахождения площади поверхности воспользуемся первой формулой. Подставим в нее значения длины, ширины и высоты параллелепипеда и произведем вычисления.

S_{полн} = 2(ab+bc+ac) = 2(2 cdot 4 + 4 cdot 5 + 2 cdot 5) = 2(8 + 20 + 10) = 2(38) = 76 : см^2

Ответ: 76 см²

Проверим ответ с помощью калькулятора .

Задача 2

Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3см 5см и 6см.

Решение

Задача аналогична предыдущей, поэтому повторим действия, подставив новые значения измерений параллелепипеда.

S_{полн} = 2(ab+bc+ac) = 2(3 cdot 5 + 5 cdot 6 + 3 cdot 6) = 2(15 + 30 + 18) = 2(63) = 126 : см^2

Ответ: 126 см²

Для проверки ответа используем калькулятор .

Задача 3

Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 9м 24м 11м.

Решение

Еще одна типовая задача. Для ее решения также воспользуемся первой формулой.

S_{полн} = 2(ab+bc+ac) = 2(9 cdot 24 + 24 cdot 11 + 9 cdot 11) = 2(216 + 264 + 99) = 2(579) = 1158 : см^2

Ответ: 1158 см²

Проверка .

Задача 4

Найдите площадь боковой поверхности прямоугольного параллелепипеда у которого a=4см, b=5см, c=7см.

Решение

В этой задаче нам необхожимо найти площадь боковой поверхности. Поэтому мы будем использовать для ее решения вторую формулу.

S_{бок} = 2(ac+bc) = 2(4 cdot 7 + 5 cdot 7) = 2(28 + 35) = 2(63) = 126 : см^2

Ответ: 126 см²

Как всегда ответ можно проверить с помощью калькулятора .

Источник

Ребра прямоугольного параллелепипеда равны 3 см, 4 см и 5 см.
а) Найдите площадь его основания и площадь боковой поверхности, то есть сумму площадей боковых граней.
б) Найдите площадь полной поверхности прямоугольного параллелепипеда.
Объясните, почему в задании «а» могут получиться три разных ответа.

reshalka.com

Математика 5 класс Никольский. Номер №506

Решение

Три разных ответа возможны из−за трех способов построения прямоугольного параллелепипеда.
Решение 1.

1) 5 * 4 = 20

(

)

− площадь основания;
2) 3 * 4 = 12

(

)

− площадь первой грани;
3) 3 * 5 = 15

(

)

− площадь второй грани;
4) (12 + 15) * 2 = 54

(

)

− площадь боковой поверхности.
Ответ:
20

− площадь основания;
54

(

)

− площадь боковой поверхности.

Решение 2.

1) 5 * 3 = 15

(

)

− площадь основания;
2) 3 * 4 = 12

(

)

− площадь первой грани;
3) 4 * 5 = 20

(

)

− площадь второй грани;
4) (12 + 20) * 2 = 64

(

)

− площадь боковой поверхности.
Ответ:
15

− площадь основания;
64

(

)

− площадь боковой поверхности.

Решение 3.

1) 3 * 4 = 12

(

)

− площадь основания;
2) 5 * 4 = 20

(

)

− площадь первой грани;
3) 3 * 5 = 15

(

)

− площадь второй грани;
4) (20 + 15) * 2 = 70

(

)

− площадь боковой поверхности.
Ответ:
12

− площадь основания;
70

(

)

− площадь боковой поверхности.

Источник