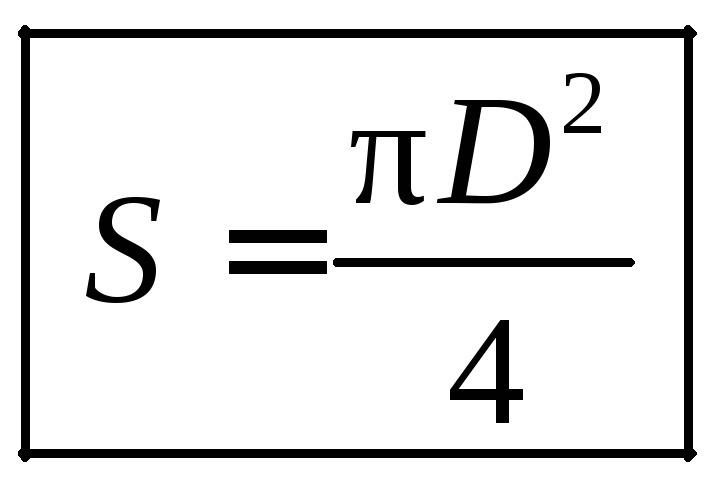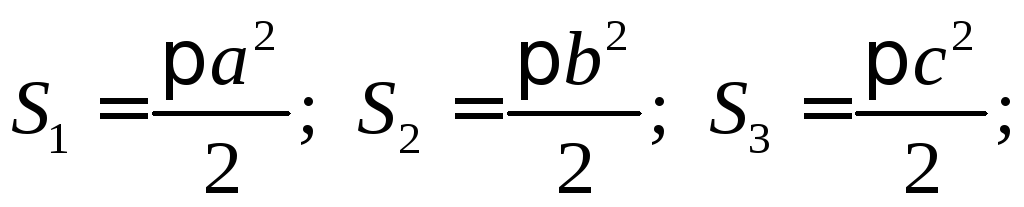Как найти площадь чечевицы - Исправление недочетов и поиск решений вместе с Examum.ru

Домашнее задание: изучить материал
пункта 110; решить задачи №№ 1109 (в,
г), 1106, 1104 (а), 1105 (а).

Урок 6 Площадь круга

Цели:вывести формулу площади круга и научить
учащихся применять ее при решении задач.

Ход урока

I. Изучение нового материала (лекция).

Провести в форме лекции доказательство
площади круга.

1. Дать определение
понятия «круг».

2. Вывести формулу
площади круга (рис. 314).

3. Записать в
тетрадях:для вычисления площади S
круга радиуса R применяется формула
.

4. В течение веков усилия многих математиков
были направлены на решение задачи,
получившей название задача о квадратурекруга: построить при помощи циркуля
и линейки квадрат, площадь которого
равна площади данного круга. Только в
конце XIX века было доказано, что такое
построение невозможно.

II. Закрепление изученного материала
(решение задач).

1. Решить задачу.
На здании МГУ установлены часы с круговым
циферблатом, имеющим диаметр примерно
8,8 м. Найдите площадь циферблата этих
часов и сравните с площадью вашей
классной комнаты.

Ответ: 60,8 м².

2. Решить задачу
№ 1118 (самостоятельно).

3. Решить задачу
№ 1119 на доске и в тетрадях.

Решение

С= 41 м;C= 2πR;D= 2R(диаметрD);

2R=D=;D=≈
13,06 (м) ≈ 13,1 м.

S_круга=πR²;
так какR=,
тоS_круга=π ∙=π ∙;

S=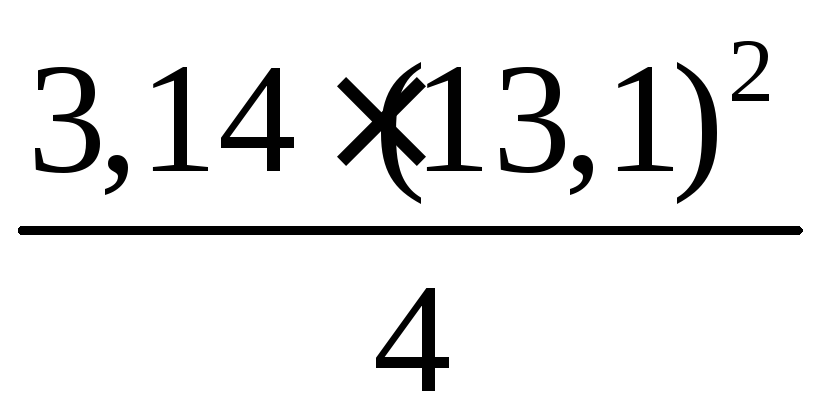≈ 133,84 (м²).

Ответ: ≈ 13,06 м;
133,84 м².

4. Решить задачу
№ 1125 на доске и в тетрадях.

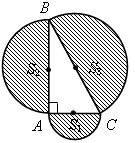
На сторонах произвольного прямоугольного
треугольника АВС,как на диаметрах,
построены полукруги. Докажите, что сумма
площадей полукругов, построенных на
катетах, равна площади полукруга,
построенного на гипотенузе.

Решение

Пусть АС= 2а,АВ= 2b,ВС= 2с, тогда радиусы соответствующих
кругов равныа,b,с.

По теореме Пифагора а²+b²=с², поэтому.

5. Решить задачу
№ 1116 (а) на доске и в тетрадях.

Решение

Центр окружности, описанной около
прямоугольного треугольника, лежит на
середине гипотенузы, а радиус описанной
окружности равен половине гипотенузы.

По теореме Пифагора находим: с²=а²+b²; тогда

R=.

Значит, S_круга=πR²
=.

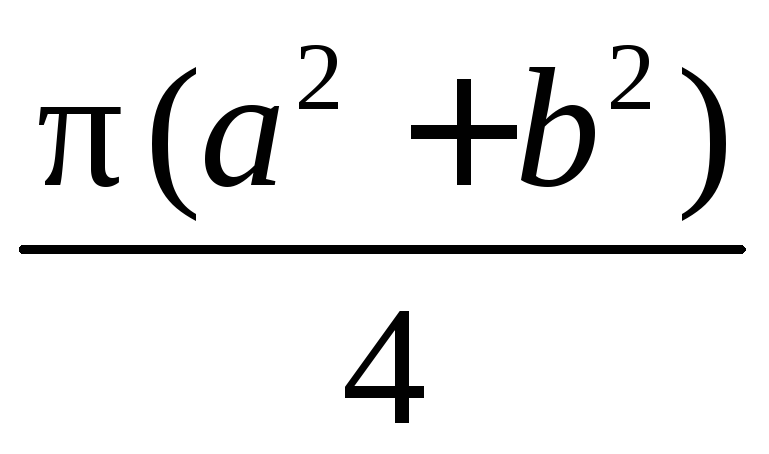
Ответ:.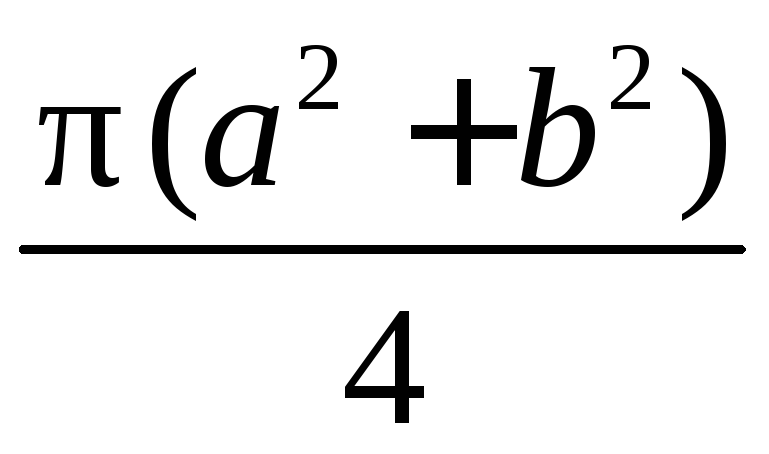

III. Итоги урока.

Домашнее задание: повторить материал
пунктов 105–110; изучить материал пункта
111; решить задачи №№ 1114, 1115, 1117 (а).

Урок 7
Площадь
кругового сектора

Цели:ввести понятие кругового сектора,
вывести формулу для вычисления площади
кругового сектора; научить применять
знания при решении задач.

Ход урока

I. Проверка изученного материала.

1. Формула длины
окружности. Выражение радиуса окружности
через длину окружности.

2. Формулы площади
круга, радиуса круга через площадь
круга, формула площади круга, выраженная
через диаметр круга.

3. Формула длины
дуги окружности.

4. Устно решить задачу
№ 1115.

II. Объяснение нового материала.

1. Ввести понятие
кругового сектора и понятие дуги
сектора
(рис. 315).

2. Вывести формулу
для вычисления площадиSкругового
сектора радиусаR, ограниченного
дугой с градусной мерой.

Так как площадь всего круга равна πR²,
то площадь кругового сектора, ограниченного
дугой в 1°, равна.

Поэтому площадь Sвыражается формулой

S=∙

3. Ввести понятие
кругового сегмента и познакомить
учащихся с нахождением площади кругового
сегмента, используя таблицу «Круговой
сегмент».

III. закрепление
изученного материала (решение задач).

1. Решить задачу.

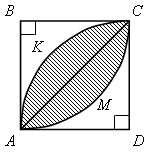
АВСD– квадрат со стороной
1 дм. Найдите площадь «чечевицы»,
заштрихованной на рисунке.

Решение

Так как сторона квадрата равна 1 дм,
то площадь квадрата АВСDравна 1 дм².

Площадь сектора DАKСравна∙ =
=
∙
90° =(дм²).

Площадь треугольника АСDравнадм².

Площадь сегмента АKСравна(дм²).

Площадь «чечевицы»: 2 ∙
≈
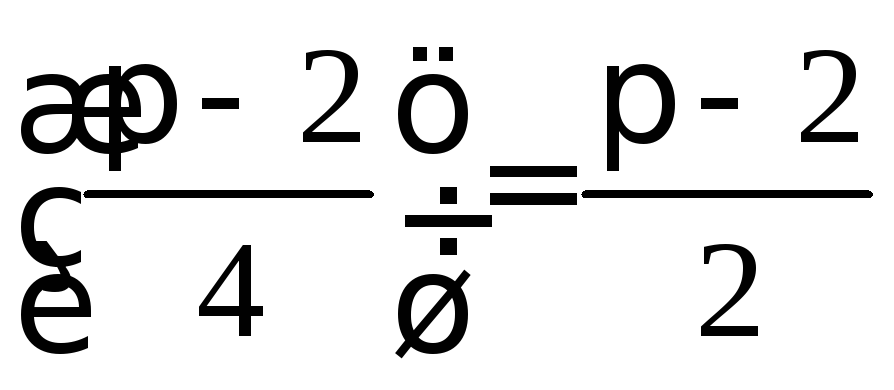
0,7 (дм²).

Ответ:≈
0,7 дм².

2. Решить задачу
№ 1126 (самостоятельно).

Решение

R= 10 см;S_круга=πR²= 100π (см²).

l== 60°;S_{сектора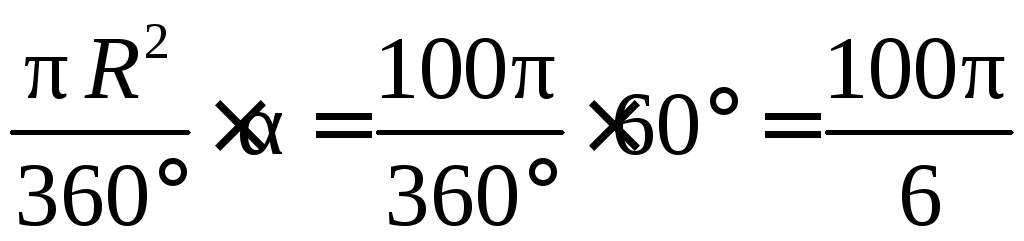}=(см²).

S=S_круга–S_{сектора}= 100π –≈
262 (cм²).

Ответ: ≈ 262 см².

3. Решить задачу
№ 1127.

Решение

 = 72°, S_{сектора}=S. Найти:R.

S=;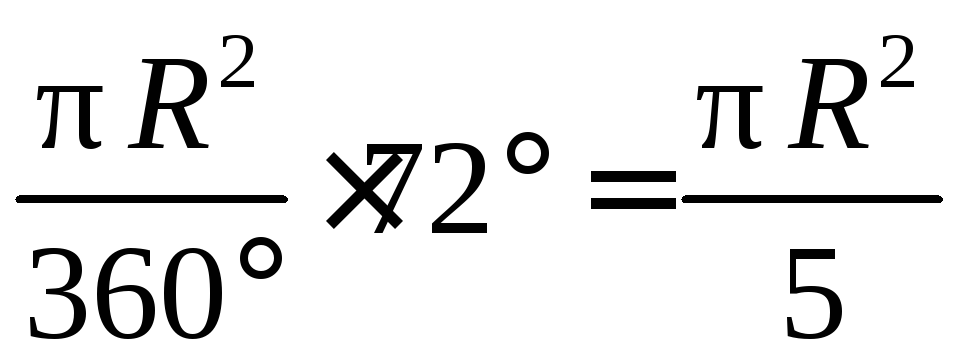
5S=πR²;R²=;R=.

Ответ:.

4. Вывести формулу
площади кольца, ограниченного двумя
окружностями с общим центром и радиусамиR₁иR₂, гдеR₁<R₂.

Решение

;S_кольца=S₂–S₁=.

5. Решить задачу
№ 1120.

Решение

R₁= 1,5 cм,R₂= 2,5 см.

S_кольца=π (2,5²
– 1,5²) = π (2,5 – 1,5)
(2,5 + 1,5) = π ∙1 ∙
4 = 4π (см²).

Ответ: 4π
см².

6. Решить задачу
№ 1122 на доске и в тетрадях.

Решение

R₁= 3 м,R₂= 3 + 1 = 4 (м);

S_{дорожки}=π
= π (4² – 3²)
= π (4 – 3) (4 + 3) = 7π (м²).

На 1 м²дорожки требуется 0,8 дм³песка; тогда 0,8 ∙ 7π= 5,6π(дм³) ≈
≈ 17,6 дм³.

Ответ: ≈ 17,6 дм³.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

урок 38

Название предмета: Геометрия
Класс: 9
УМК (название учебника, автор, год издания): Геометрия 7 – 9. учебник для 7 – 9 классов средней школы, Л.С. Атанасян и др., 2013 г.
Уровень обучения: базовый
Тема урока: Площадь кругового сектора (Слайд 1)
Общее количество часов, отведенное на изучение темы: 1 час
Место урока в системе уроков: третий урок по теме «Длина окружности и площадь круга», комбинированный урок
Цели и задачи урока: ввести понятие кругового сектора, вывести формулу для вычисления площади кругового сектора; научить применять знания при решении задач. (Слайд 2)
Планируемые результаты: обучающиеся научатся применять знания о круговом секторе при решении задач.
Техническое обеспечение урока: мел, доска, проектор, экран, транспортир
Дополнительное методическое и дидактическое обеспечение урока (возможны ссылки на интернет-ресурсы)
Содержание урока

I. Организационный момент
Приветственное слово учителя:
Начинается урок,
Он пойдёт ребятам впрок.
Постарайтесь всё понять -
И внимательно считать.
- Здравствуйте, ребята! Сегодня на уроке мы познакомимся с понятием «круговой сектор», выведем формулу для вычисления площади кругового сектора, научимся применять полученные знания при решении задач.
II. Проверка изученного материала (Устный опрос) (Слайд 3)
1. Формула длины окружности. Выражение радиуса окружности через длину окружности.
2. Формулы площади круга, радиуса круга через площадь круга, формула площади круга, выраженная через диаметр круга.
3. Формула длины дуги окружности.
4. Устно решить задачу № 1115.
III. Объяснение нового материала. (Обучающиеся конспектируют)
1. Ввести понятие кругового сектора и понятие дуги сектора
(рис. 315 учебника). (Слайд 4)
Определение: Круговым сектором или просто сектором называется часть круга, ограниченная дугой двумя радиусами, соединяющими концы дуги с центром круга. Дуга, которая ограничивает сектор, называется дугой сектора. На рисунке 315 изображены два сектора с дугами ALB и AMB.
2. Вывести формулу для вычисления площади S кругового сектора радиуса R, ограниченного дугой с градусной мерой. (Слайд 5)
Так как площадь всего круга равна πR2, то площадь кругового сектора, ограниченного дугой в 1°, равна .
Поэтому площадь S выражается формулой

2. Ввести понятие кругового сегмента и познакомить учащихся с нахождением площади кругового сегмента, используя таблицу «Круговой сегмент». (Слайд 6)

Круговой сегмент - часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L - длина дуги сегмента
c- хорда
R- радиус
a- угол сегмента
h- высота
Площадь кругового сегмента: Sсегм= Sсект−Sтреуг, (Слайд 7) или
Площадь сегмента круга, окружности, если угол в градусах

Площадь сегмента круга, окружности, если угол в радианах:
(Слайд 8)
IV. закрепление изученного материала (решение задач оформляется учителем на доске, ученики записывают в тетрадях).
1. Решить задачу. (Слайд 9)
АВСD – квадрат со стороной 1 дм. Найдите площадь «чечевицы», заштрихованной на рисунке.
Решение
Так как сторона квадрата равна 1 дм, то площадь квадрата АВСD равна 1 дм2.

Площадь сектора DАKС равна ∙  =
= ∙ 90° = (дм2).
Площадь треугольника АСD равна дм2.
Площадь сегмента АKС равна (дм2).
Площадь «чечевицы»: 2 ∙ ≈ 0,7 (дм2).
Ответ: ≈ 0,7 дм2.
2. Решить задачу № 1126 (самостоятельно). (Слайд 10)
Решение
R = 10 см; Sкруга = πR2 = 100π (см2).
l = 60°; Sсектора = (см2).
S = Sкруга – Sсектора = 100π –≈ 262 (cм2).
Ответ: ≈ 262 см2.
3. Решить задачу № 1127(один из учеников выполняет у доски, класс работает над задачей в тетрадях).
Решение
Sсектора = S. Найти: R.
S =; 5S = πR2; R2 =; R =.
Ответ: .
4. Вывести формулу площади кольца, ограниченного двумя окружностями с общим центром и радиусами R1 и R2, где R1 < R2. (Слайд 11)
Решение
; Sкольца = S2 – S1 = .

5. Решить задачу № 1120.
Решение
R1 = 1,5 cм, R2 = 2,5 см.
Sкольца = π (2,52 – 1,52) = π (2,5 – 1,5) (2,5 + 1,5) = π ∙ 1 ∙ 4 = 4π (см2).
Ответ: 4π см2.

V. Подготовка к ОГЭ (Слайд 12)
Задача. Найдите площадь S закрашенного сектора, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S/π

В первую очередь нам потребуется формула площади круга:
S = πR2
где R — радиус нашего круга. Эту формулу надо знать наизусть. Без нее задачи B5 на площадь круга не решаются вообще.
Но есть и другая проблема. Давайте внимательно посмотрим на рисунок. Для вычисления площади круга (а затем — и сектора) нам надо знать радиус.
Ну и где же здесь радиус? Если мы проведем горизонтальную ось, то получим непонятное число на отрезке [2; 3]. Конечно, можно сказать, что это число ближе к x = 3, но чему именно равно это число, нам неизвестно. А следовательно, использовать эту примерную оценку для решения задачи мы не можем. Надо действовать как-то иначе.
(Слайд 13) Например, давайте пройдемся по нашей окружности и отметим на ней те точки, которые лежат в узлах координатной сетки. Таких точек будет 4 штуки:

Что дают нам эти точки? А дело в том, что мы можем точно указать, на сколько клеток эти точки отстоят от центра окружности. Например, рассмотрим точку A и центр окружности O:

Мы видим, что точка A отстоит от точки O на 2 клетки по горизонтали и на 2 клетки по вертикали. Получаем прямоугольный треугольник с катетами 2 и 2. Кроме того, гипотенуза нашего прямоугольного треугольника как раз и является радиусом круга, площадь сектора в котором нам и требуется найти.
По теореме Пифагора получаем:
R2 = 22 + 22 = 4 + 4 = 8
Теперь мы знаем квадрат радиуса круга: R2 = 8. Следовательно, зная радиус, мы можем найти площадь всего круга. Достаточно просто подставить найденный радиус в формулу площади. Получим:
S = πR2 = π · 8 = 8π
Следующий шаг — мы должны понять, какую часть площади круга занимает закрашенный сектор. Для этого давайте схематично разделим исходный круг на 8 равных частей, как пиццу. На полученной разметке закрасим те кусочки, которые входят в состав искомого сектора. Получится вот такая картинка:

Получается, что закрашенных кусочков k = 3. При этом всего кусков было n = 8. Поскольку площади всех секторов, возникающих при «разрезании» исходного круга, одинаковы, можно найти площадь каждого из них, разделив общую площадь на 8. Затем надо умножить полученное число на 3, поскольку в искомом секторе содержится 3 таких одинаковых кусочка. Подставляем все в формулу:

Но это еще не все! В данной задаче нас просят указать величину S/π. Подставляем и получаем:
3π/π = 3
Вот мы и нашли ответ. Площадь сектора, деленная на π, равна 3. Как видите, ничего сложного в этой задаче нет. Все, что от нас требуется — правильно выбирать точки на окружности (надо, чтобы они лежали в узлах координатной стеки), а затем подставлять полученные числа в теорему Пифагора.Конец формы
IV. Итоги урока. (Слайд 14)
Домашнее задание: выучить материал пунктов 110–112; повторить материал пунктов 105–109; ответить на вопросы 1–12 на с. 290; решить задачи № 1121, 1128, 1124.

Автор(ы): Дроженко Н. А.

Скачать: Геометрия 9кл — урок 38.docx

Конспект

Название предмета: геометрия
Класс: 9
УМК (название учебника, автор, год издания): Геометрия, 7-9: учебник для общеобразовательных учреждений/ (Л.С. Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.) – 18-е изд.- М.: Просвещение, 2012 г.
Уровень обучения базовый
Тема урока: Площадь круга и кругового сектора.
Общее количество часов, отведенное на изучение темы: 1
Место урока в системе уроков по теме: 7 урок в системе уроков по теме: Длина окружности и площадь круга (12 ч)
Цель урока: знакомство с формулами площади круга и кругового сектора и их применение при решении задач.
Задачи урока:
Образовательная: ввести формулу, выражающую площадь круга и кругового сектора; закрепить знание формул при решении задач.
Развивающая: - формирование познавательной самостоятельности учащихся, развитие памяти, математической речи, любознательности.
Воспитательная: - воспитание внимания, самоконтроля, интереса к предмету.
Планируемые результаты: выводить формулы для вычисления площади круга и площади кругового сектора. Применять эти формулы при решении задач.
Техническое обеспечение урока: компьютер, мультимедийный проектор, презентация к уроку в формате PowerPoint.
Содержание урока:

I. Организационный момент.
Проверка готовности учащихся к уроку.
II. Актуализация знаний учащихся (повторение теоретического материала):
1. Запишите, какие формулы используются для вычисления длины окружности; длины дуги окружности?
2. Чему равно значение числа π?
III. Проверка домашнего задания.
№1106
1) Что означает один оборот колеса с математической точки зрения?
2) Чему равно расстояние, пройденное автомобилем, если колесо автомобиля
сделало один оборот?

Ответ: 0,63 м.
№1111
Что нужно знать для вычисления длины дуги?
2) Каким образом можно вычислить радиус камня?
Ответ: ≈ 59,189 (см)

IV. Изучение нового материала.
Как называется геометрическая фигура ограниченная окружностью? (круг) Вспомните формулу для вычисления площади правильных многоугольников. S= Pr.
Начертите окружность и впишите в неё сначала треугольник, затем квадрат, пятиугольник, шестиугольник, восьмиугольник и сделайте вывод: какой многоугольник больше похож на окружность. (Чем больше сторон у правильного вписанного многоугольника, тем многоугольник становится похожим на окружность)
Т.о. за периметр можно взять длину окружности (периметр сумма всех сторон). Затем запишем формулу длины окружности С = R, и подставим в формулу площади правильного многоугольника S=.
Итак, площадь круга S = R2
Начертим круг и проведем два радиуса. Получим сектор MОN.
Круговым сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющимися концы дуги с центром круга.
Необходимо найти его площадь.
Как вы думаете, от чего будет зависеть площадь сектора?
Итак, мы с вами выяснили, что площадь круга зависит от радиуса круга.
Тогда, если площадь круга S =R 2 , а градусная мера окружности 360o , то чему будет равна площадь сектора, ограниченная дугой в 1o? 5o? 60o? ?

Мы получаем формулу площади сектора: S =

V. Закрепление изученного материала (решение задач)
№ 1
Диаметр основания Царь-колокола, находящегося в московском Кремле, равен 6,6 м. Найдите площадь основания колокола.
№ 2
Длина окружности цирковой арены равна 41 м. Найдите диаметр и площадь арены.
№ 3
Из круга, радиус которого 7 см, вырезан сектор с дугой в 600.
Найдите площадь оставшейся части круга.
VI. Самостоятельная работа.
1 вариант
1. Начертить окружность произвольным радиусом, измерить её радиус и вычислить площадь круга.
2. Провести два радиуса ОM и ОN, измерить градусную меру угла MОN и вычислить площадь сектора MОN.
2 2 вариант
1. Начертить окружность произвольным радиусом, измерить её радиус и вычислить площадь круга.
2. Провести два радиуса ОК и ОР, измерить градусную меру угла КОР и вычислить площадь сектора КОР.
Обсуждение результатов самостоятельной работы
VII. Домашнее задание.
с. 288 – 289 п. 111; 112, № 1114; 1120.
VIII. Рефлексия. Итоги урока.
По какой формуле вычисляются площадь круга?
По какой формуле вычисляется площадь кругового сектора?
Что сегодня нового было на уроке?
Что было самым трудным для тебя на уроке?
Что тебе удалось на уроке?
Над чем ещё нужно поработать?

Автор(ы): Жакупова Г. Е.

Скачать: Геометрия 9кл — Конспект.doc

Конспект 1

Название предмета геометрия

Класс 9

УМК (название учебника, автор, год издания) Геометрия 7-9, Л.С. Атанасян, 2011 г.

Уровень обучения (базовый, углубленный, профильный) базовый

Тема урока: Площадь круга и кругового сектора

Общее количество часов, отведенное на изучение темы 12 часов

Место урока в системе уроков по теме номер 7

Цель урока - Дать представление о выводе формулы площади круга и на её основе получить формулу площади кругового сектора. Показать применение формул к решению задач.

Задачи урока вывести формулы площади круга и кругового сектора, способствовать формированию умения применять полученные формулы для решения задач. Развивать логическое мышление учащихся, математическую речь и навыки самостоятельной работы. Воспитывать умение высказывать свое мнение, формировать способность к позитивному сотрудничеству.

Планируемые результаты:
– знают формулы площади круга, кругового сектора и площади кольца;
– умеют изображать геометрический рисунок по условию задачи, связанный с площадью круга, кругового сектора и кольца;
– умеют применять формулы площади круга, кругового сектора и площади кольца для решения несложных задач.
Техническое обеспечение урока конспект урока, учебник, доска, проектор, компьютер, сигнальные карточки.
Дополнительное методическое и дидактическое обеспечение урока (возможны ссылки на интернет-ресурсы):
Геометрия. 9 класс: Поурочные планы (по учебнику Л.С. Атанасяна и др. «Геометрия. 7-9 классы») / Авт.-сост. Т.Л. Афанасьева, Л.А. Тапилина. – Волгоград: Учитель
Н.Ф. Гаврилова. Поурочные разработки по геометрии: 9 класс. – М.: ВАКО, 2011
Геометрия 7-9 классы: Задачи на готовых чертежах. Составитель: М.Р. Рыбникова. – Луганск: Янтарь, Учебная книга, 2003.

Содержание урока.
Ход урока
I. Организационный этап
Цель: создать благоприятный психологический настрой на работу.
II. Актуализация знаний учащихся
1. Проверка домашнего задания.
Цель: проверить готовность класса к уроку.
Обсудить решение задач, вызвавших наибольшие затруднения у учащихся.
2. Индивидуальная работа по карточкам ( предложить 7 ученикам).Работают под копирку. После того как работа будет выполнена, один экземпляр сдать учителю, а второй оставить себе, затем выполнить самопроверку по готовым решениям.
Цель: проверить степень усвоения темы «Длина окружности. Длина дуги окружности» отдельными учащимися.
Карточка 1
1)Длина окружности равна 15. Найдите радиус этой окружности.
2) Найдите длины дуг, на которые разбивают окружность два радиуса, если угол между ними равен 720, а радиус окружности равен 6 дм.
Карточка 2
1) Найдите длину окружности, радиус которой равен 5.
2) На окружности с центром О отмечены точки A и B так, что угол AOB равен 1220. Длина меньшей дуги AB равна 61. Найдите длину большей дуги AB.
Карточка 3
1)Длины сторон прямоугольника равны 6 и 8. Найдите длину окружности, описанной около этого прямоугольника.
2) Радиус окружности равен 6. Найдите длину дуги окружности, соответствующую вписанному углу этой окружности, если вписанный угол равен 340.
Карточка 4
1) Найдите длину окружности, в которую вписан квадрат со стороной 5 см.
2) В окружность вписан правильный треугольник с площадью 12 см2. Найдите длину этой окружности.

Карточка 5
1) Найдите длину дуги окружности радиуса 9 м, если градусная мера дуги равна 1200.
2) Длина хорды окружности равна 88, а расстояние от центра окружности до этой хорды равна 33. Найдите диаметр окружности.
Карточка 6
1) Длина дуги окружности равна 3, а её радиус равен 8. Найдите градусную меру этой дуги.
2) Периметр квадрата, вписанного в окружность равен 48 см. Найдите длину этой окружности.
Карточка 7
1) Найдите радиус окружности, если длина дуги окружности равна 6, а её градусная мера равна 600.
2) Найдите длину окружности, вписанной в квадрат, если периметр квадрата равен 48см.
3. Задачи на готовых чертежах: (для остальных учащихся) Работают самостоятельно, правильность решения проверить по готовым ответам, затем обсудить решения задач, вызвавших наибольшие затруднения у учащихся.
Цель: способствовать совершенствованию навыков решения задач на готовых чертежах по теме «Длина окружности. Длина дуги окружности».
1. Рис.1 ABCD – квадрат. SABCD = 16.
Найти длину окружности.
2. Рис.2 KM –диаметр окружности. MH = 9, LH = 6.
Найти длину полуокружности KLM.
3. Рис.3 ∆ ABC - правильный. Длина дуги AB = 4.
Найти: S∆ABC.
4. Рис.4 PR – диаметр окружности, О – центр окружности, дуги PN, NG и GR равны по 4. Углы PEN и GFR прямые.
Найти длину отрезка NG.

Рис. 1 Рис. 2

Рис.3 Рис.4
Ответы к задачам на готовых чертежах:
1. 4 R;
2. 6,5;
3. 27;
4. 12.

III. Сообщение темы урока и целеполагание.
Цель: сообщить тему урока и организовать постановку цели учебной деятельности, выбор способа и средств реализации.
IV. Изучение нового материала
Ввести понятие круга.
Определение. Кругом называется часть плоскости, ограниченная окружностью.
Если круг с центром О имеет радиус, равный R, то он содержит точку О и все точки плоскости, находящиеся на расстоянии, не превосходящем R.
Вывод формулы площади круга. (В виде лекции по рисунку 314 учебника)
Цель: дать представление о выводе формулы площади круга.
План лекции:
Рассмотреть: правильный n-угольник с площадью Sn;
Окружность, описанную около этого n-угольника и окружность, вписанную в этот n-угольник и сравнить площади кругов, увеличивая количество сторон правильного n-угольника неограниченно.
Так как r = R cos , то при n R cos = R 1 = R. При неограниченном увеличении сторон многоугольника вписанная в него окружность стремится к описанной окружности, поэтому площадь вписанного круга будет стремиться к площади описанного круга при n n будет также стремиться к площади описанного круга.
Sn = Pn rn ; Pn –периметр многоугольника; rn - радиус вписанной окружности;
Учитывая, что rn Pn 2R, Sn S при n , то S = 2 = .
Итак, формула для вычисления площади круга радиуса R:
S = .
Ввести понятие кругового сектора.
Определение. Круговым сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Вывод формулы площади кругового сектора предложить для самостоятельного решения учащимся (обсудить различные способы решения и записать один из них).
Цель: способствовать формированию умения самостоятельного приобретения знаний.
Возможные наводящие вопросы:
1. Чему равна градусная мера окружности?
2. Как найти площадь кругового сектора, ограниченного дугой в 10.
3. Как найти площадь кругового сектора, ограниченного дугой α0.
Sкруг.сект. = .
V. Закрепление изученного материала
Цель: способствовать формированию умения применять полученные знания для решения задач.
1. Вывести формулу площади кольца, ограниченного двумя окружностями с общим центром и радиусами R1 и R2, где R1 R2.
Решение
S1 = R12 ; S2 = R22; Sкольца = S2 – S1 = R22 - R12 = (R22 – R12).
Sкольца = (R22 – R12).
2. №1116(в)
Дано: ∆ABC-равнобедренный, AC-основание = a, BH - высота = h, w(O,R) - окружность, описанная около треугольника.
Найти площадь круга.
Решение

О – центр описанной окружности, О є ВН, точка О разобьёт высоту, проведённую к основанию равнобедренного треугольника на два отрезка. Пусть ВО = x, OH = h – x. BO = AO = OC = R = x, так как О – центр описанной окружности.
Рассмотрим ∆АОН с прямым углом Н и применим теорему Пифагора.
АО =х; АН = ; OH =h – x.
x2 = (h – x)2 + ;
x2 = h2 – 2hx + x2 +;
2hx = h2 + ;
x = ;
R2 = ;
Sкруга = .
Наводящие вопросы:
1. Где расположен центр окружности, описанной около треугольника (в точке пересечения серединных перпендикуляров).
2. Можно ли считать заданную высоту серединным перпендикуляром? (да, так как высота, проведенная к основанию равнобедренного треугольника, является и его медианой).
3. Какой треугольник нужно выбрать для решения задачи ? (АОН или НОС, так как в них обозначены все элементы для теоремы Пифагора с одной неизвестной величиной).
VI. Самостоятельная работа
Цель: способствовать совершенствованию навыков решения задач с применением формул площади круга и кругового сектора.
Для менее подготовленных учеников - №1119, 1120,1126
Для более подготовленных учеников - №1116(б), 1126, 1121
VII. Подведение итога урока
Цель: организовать рефлексию и самооценку собственной деятельности.
- какую цель мы ставили?
- достигли ли цели?
- чему вы научились?
- оцените свою деятельность на этом уроке (с помощью сигнальных карточек).
Домашнее задание:
Для менее подготовленных учеников – 1114,1116(а),1122
Для более подготовленных учеников – 1117(б), 1127 и дополнительная задача
Постройте круг, площадь которого в 4 раза больше площади данного круга. Во сколько раз длина окружности, ограничивающая первый круг, меньше длины окружности, ограничивающей второй круг?

Могу всё сам

Могу частично самостоятельно и частично с помощью учителя

Могу с помощью учителя

Затрудняюсь в выполнении заданий
Сигнальные карточки

Автор(ы): Гончарова Н. Н.

Скачать: Геометрия 9кл — Конспект 1.docx

Конспект 2

 
Название предмета  геометрия
Класс 9
УМК (название учебника, автор, год издания) Геометрия 7-9, Л.С. Атанасян, 2011 г.
Уровень обучения (базовый, углубленный, профильный) базовый
Тема урока Площадь круга и кругового сектора
Общее количество часов, отведенное на изучение темы  12 часов
Место урока в системе уроков по теме номер 8
Цель урока - Совершенствовать навыки решения задач с использованием формул площади круга и кругового сектора, длины окружности и длины дуги окружности.
Задачи урока - Способствовать совершенствованию навыков решения задач с применением формул длины окружности и длины дуги окружности, площади круга и кругового сектора. Развивать логическое мышление учащихся, математическую речь и навыки самостоятельной работы. Воспитывать умение высказывать свое мнение, формировать способность к позитивному сотрудничеству.
Планируемые результаты:
– знают формулы длины окружности, длины дуги окружности, площади круга, кругового сектора и площади кольца; формулы для вычисления стороны правильного многоугольника; 
– умеют изображать геометрический рисунок по условию задачи, связанный с площадью круга, кругового сектора и кольца;
– умеют применять изученные формулы для решения задач.
Техническое обеспечение урока конспект урока, учебник, доска, проектор, компьютер, сигнальные карточки.
Дополнительное методическое и дидактическое обеспечение урока (возможны ссылки на интернет-ресурсы):
Геометрия. 9 класс: Поурочные планы (по учебнику Л.С. Атанасяна и др. «Геометрия. 7-9 классы») / Авт.-сост. Т.Л. Афанасьева, Л.А. Тапилина. – Волгоград: Учитель
Н.Ф. Гаврилова. Поурочные разработки по геометрии: 9 класс. – М.: ВАКО, 2011
Геометрия 7-9 классы: Задачи на готовых чертежах. Составитель: М.Р. Рыбникова. – Луганск: Янтарь, Учебная книга, 2003. 

Содержание урока
I. Организационный момент
Цель: создать благоприятный психологический настрой на работу.
II. Актуализация знаний учащихся
Цель: проверить готовность класса к работе (умение выводить формулы площади круга, кругового сектора и кольца, умение находить ошибки в решении задачи и объяснять их, знание формул по изучаемой теме).
1.  Проверка домашнего задания.
а) Вызвать 3-х учащихся к доске для выведения формул площади: а) круга, б) кругового сектора, в) кольца.
б) На доске подготовлено решение домашних задач с ошибками. Задание учащимся – найти ошибки.
2. Фронтальная работа с классом.
- какая формула используется для вычисления:
длины окружности;
длины дуги окружности;
площади круга;
площади кругового сектора;
стороны правильного n-угольника;
радиуса вписанной в правильный n-угольник окружности;
площади правильного n-угольника?
- чему равен угол правильного  n-угольника?
- чему равна сумма внешних углов правильного n-угольника?
- где расположен центр окружности, описанной около треугольника?
- где расположен центр окружности, вписанной в треугольник?
- чему равен угол, вписанный в окружность?
Заслушать ответы учеников, работавших у доски.
III. Сообщение темы урока и целеполагание.
Цель: сообщить тему урока и организовать постановку цели учебной деятельности, выбор способа и средств реализации.
IV. Решение задач на готовых чертежах (самостоятельно под копирку, после того, как один экземпляр сдали учителю, самопроверка, затем обсудить решение задач, вызвавших наибольшие затруднения у учащихся).
Цель: совершенствовать навыки решения задач на готовых чертежах на применение формул площади круга и кругового сектора.







Рис.1                                                                                          Рис.2                                                            





ри.



    Рис.3                                                                                  Рис.4





                                                                        Рис.5           Рис.6

Найдите площади заштрихованных фигур:
Рис.1     Дано: R = 12;
Рис.2     Дано: R1 = 13, R2 = 11;
Рис.3     Дано: R1 = 15, R2 = 4, R3 = 7;
Рис.4     Дано: R = 4;
Рис.5     Дано: R2 = 3;
Рис.6     Дано: R = 5, CB = 8, угол ACB = 900.
Ответы к задачам на готовых чертежах:
Рис.1              48;
Рис.2              48;
Рис.3              160;
Рис.4               +8;
Рис.5             27;
Рис.6              25 - 24.
V. Тест 
Цель: проверить степень усвоения материала по темам «Длина окружности и длина дуги окружности», «Площадь круга и кругового сектора».
I Вариант
1. Длина окружности равна 5. Найдите площадь ограниченного ею круга.
а) 6,25;                     б) 2,5;             в) 25.
2. Длина дуги окружности равна 4, а радиус равен 6. Найдите градусную меру этой дуги.
а) 1600                       б) 1500               в) 1200.
3. Найдите площадь кругового сектора радиуса 4, если его центральный угол равен 150.
а)                                б) 2                в) .
4. Сторона правильного треугольника равна 36. Найдите радиус окружности, описанной около этого треугольника.
а) 36                             б) 6                     в) 72.
5. Площадь круга равна . Найдите длину его окружности.
а) 50                       б) 25                      в) 50.
6. К окружности с центром в точке О проведены касательная AB секущая AO. Найдите радиус окружности, если  AB = 21,  AO = 75












а) 78;            б) 25;         в) 72.

7. Найдите площадь сектора круга радиуса 24, длина дуги которого равна3.
а) 45                      б) 36                       в) 36.
8. Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны  и .
а) 88                      б) 88                        в) 16.
9. В треугольнике ABC AB =18, угол C = 450.  Найдите радиус описанной около треугольника ABC окружности.
а) 9                     б) 9                        в) 18.
10. Площадь сектора круга радиуса 22 равна 165. Найдите длину его дуги.
а) 15                       б) 15                  в) 121.
II Вариант
1. Длина окружности равна 3. Найдите площадь ограниченного ею круга.
а) 9;                      б) 1,5;                в) 2,25. 
2. Длина дуги окружности равна 7, а радиус равен 12. Найдите градусную меру этой дуги.
а) 1400                     б) 1050             в) 1200. 
3. Найдите площадь кругового сектора радиуса 13, если его центральный угол равен 400.
а)                        б)                  в) .
4. Сторона правильного треугольника равна 26. Найдите радиус окружности, описанной около этого треугольника.
а) 26                            б) 13                       в) 52.
5. Площадь круга равна. Найдите длину его окружности. 
а) 22                     б) 11                           в) 22.
6. Отрезок AB = 18 касается окружности радиуса 80 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD









а) 4            б) 2            в) 6.
7. Найдите площадь сектора круга радиуса 16, длина дуги которого равна 1.
а) 8                          б) 64                        в) 8.
8. Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны  и .
а) 16                          б) 32                      в) 32.
9. В треугольнике ABC AB =3, угол C = 300.  Найдите радиус описанной около треугольника ABC окружности.
а) 6                               б) 3                          в) 3.
10. Площадь сектора круга радиуса 25 равна 175. Найдите длину его дуги.
а) 14         б) 14             в) 125.
Ответы к тесту
Номер задания
1
2
3
4
5
6
7
8
9
10
Вариант I 
а
в
в
а
в
б
в
б
а
а
Вариант II
в
б
б
а
в
б
в
в
в
б

V. Подведение итога урока
Цель: организовать рефлексию и самооценку собственной деятельности.
- какую цель мы ставили?
- достигли ли цели?
- чему вы научились?
- оцените свою деятельность на этом уроке (с помощью сигнальных карточек).
Домашнее задание:
Для менее подготовленных учеников – 1123,1117(а),1124
Для более подготовленных учеников – 1124, 1125 и дополнительная задача
Окружности с радиусами 8см и 24см касаются друг друга внешне, AB их общая касательная. Найдите площадь фигуры, заключенной между этими окружностями и их общей касательной AB (A и B – точки касания).

Могу всё сам


















Могу частично самостоятельно и частично с помощью учителя












Могу с помощью учителя

Автор(ы): Гончарова Н. Н.

Скачать: Геометрия 9кл — Конспект 2.docx

Решение задач по теме «Площадь кругового сектора»

Автор(ы): Лесничая О. В.

Скачать: Геометрия 9кл — Решение задач по теме «Площадь кругового сектора».docx

Источник

Настоящий стандарт распространяется на стальные горячекатаные с односторонним ромбическим и чечевичным рифлением листы общего назначения.

— Площадь поверхности рассчитана с 2-х сторон.
— Площадь поверхности расчетная (в ГОСТ данные о площади отсутствуют).

Толщина основания листа, мм:

Вид рифления:

Выбор отображения общей массы:

Площадь листа (S), м²:

Масса 1 м², кг:
0

Площадь поверхности 1 т, м²:
0

Масса общая, кг:
0

Площадь поверхности общая, м²:
0

1. Толщина листов с односторонним ромбическим и чечевичным рифлением определяется по толщине основания листа S в миллиметрах.

2. Для листов, прокатанных на станах полистной прокатки, в средней части ширины листа допускается толщина основания на 0,2 мм выше плюсового предельного отклонения.

3. Ширина основания рифлей b, угол при вершине рифлей φ, диагонали ромба t1 + t2, угол расположения рифлей на плоскости листа φ1, расстояние между рифлями t, длина рифлей l, радиус закругления рифлей R на готовых листах не контролируются и даны для расчетов при изготовлении инструмента.

4. Масса 1 м2 листа определена по номинальным размерам листов, высоте рифлей, равной 0,2 толщины листа, малой диагонали ромба, равной 27,5 мм, большей диагонали ромба, равной 65 мм. Плотность стали — 7,85 г/см3.

Источник

Предлагаем Вашему вниманию статью, посвященную динамике посевных площадей, валовых сборов и урожайности чечевицы в России. Здесь представлены как общие по стране показатели (за 2001-2019 гг.), так и статистика по регионам (ТОП-20 регионов с наибольшими размерами площадей и сборов за 2019 год, урожайность в ключевых регионах выращивания в 2019 году).

Важно! Под заказ возможна подготовка и предоставление комплексного маркетингового исследования российского рынка чечевицы. Подробнее — по ссылке: Обзор российского рынка чечевицы.

Все готовые исследования рынка зерна публикуются в базе готовых исследований по ссылке База готовых исследований. Зерно.

Посевные площади чечевицы в 2001-2019 гг.

В 2019 году, по данным Росстата, посевные площади чечевицы составили 137,1 тыс. га, что на 49,5% (на 134,3 тыс. га) меньше, чем в 2018 году.

За 5 лет они выросли на 399,6% (на 109,6 тыс. га), за 10 лет — на 1 233,9% (на 126,8 тыс. га), к 2001 году — на 2 223,4% (на 131,2 тыс. га).

Посевные площади чечевицы по федеральным округам России в 2019 году:

В 2019 году, по отношению к 2018 году, произошло сокращение площадей выращивания чечевицы во всех федеральных округах страны.

В 2019 году в Сибирском ФО размеры площадей составили 62,5 тыс. га (45,6% всех посевов чечевицы в России), в Приволжском ФО — 58,8 тыс. га (42,9%), в Южном ФО — 8,5 тыс. га (6,2%), в Северо-Кавказском ФО — 3,1 тыс. га (2,2%), в Центральном ФО — 3,1 тыс. га (2,2%), в Уральском ФО — 1,1 тыс. га (0,8%), в Северо-Западном ФО — 0,02 тыс. га (0,01%).

Рейтинг регионов по размеру площадей чечевицы (ТОП-20) в 2019 году:

1. Лидером по посевным площадям чечевицы в 2019 году является Алтайский край, где посевные площади составили 49,4 тыс. га (36,1% в общих площадях). По отношению к предыдущему году, они сократились на 38,5% (на 30,9 тыс. га).

2. Саратовская область (в 2019 году засеяно 40,0 тыс. га, 29,2% от общих по РФ размеров).

3. Омская область (11,4 тыс. га, 8,3%).

4. Пензенская область (6,1 тыс. га, 4,4%).

5. Оренбургская область (5,5 тыс. га, 4,0%).

6. Республика Крым (4,0 тыс. га, 2,9%).

7. Самарская область (3,2 тыс. га, 2,3%).

8. Волгоградская область (3,1 тыс. га, 2,3%).

9. Ставропольский край (3,0 тыс. га, 2,2%).

10. Республика Башкортостан (2,1 тыс. га, 1,5%).

11. Новосибирская область (1,7 тыс. га, 1,2%).

12. Республика Татарстан (1,2 тыс. га, 0,9%).

13. Курская область (1,1 тыс. га, 0,8%).

14. Орловская область (1,1 тыс. га, 0,8%).

15. Ростовская область (1,1 тыс. га, 0,8%).

16. Челябинская область (1,0 тыс. га, 0,7%).

17. Ульяновская область (0,7 тыс. га, 0,5%).

18. Рязанская область (0,5 тыс. га, 0,3%).

19. Краснодарский край (0,4 тыс. га, 0,3%).

20. Тульская область (0,2 тыс. га, 0,1%).

Посевные площади чечевицы в других регионах составили 0,3 тыс. га (0,3% от общих размеров площадей).

Отметим, что статистика посевных площадей, валовых сборов и урожайности чечевицы в России по регионам РФ представлена в динамике 2001-2019 гг. в формате Excel по ссылке: Чечевица. Посевные площади, валовые сборы и урожайность по регионам РФ в 2001-2019 гг.

Валовые сборы чечевицы в 2001-2019 гг.

В 2019 году, по данным Росстата, валовые сборы чечевицы в хозяйствах всех категорий составили 116,6 тыс. тонн, что на 40,1% (на 78,1 тыс. тонн) меньше, чем в 2018 году.

За 5 лет сборы выросли на 477,2% (на 96,4 тыс. тонн), за 10 лет — на 1 523,1% (на 109,4 тыс. тонн), к 2001 году — на 2 280,0% (на 111,7 тыс. тонн).

Валовые сборы чечевицы по федеральным округам России в 2019 году:

Сибирский ФО в 2019 году находится на первом месте по валовым сборам чечевицы — 54,7 тыс. тонн (46,9% в общих сборах чечевицы в России), в Приволжском ФО собрали — 46,9 тыс. тонн (40,2%), в Южном ФО — 5,9 тыс. тонн (5,1%), в Центральном ФО — 5,7 тыс. тонн (4,9%), в Северо-Кавказском ФО — 2,7 тыс. тонн (2,3%), в Уральском ФО — 0,7 тыс. тонн (0,6%), в Северо-Западном ФО — 0,02 тыс. тонн (0,02%).

Рейтинг регионов по валовым сборам чечевицы (ТОП-20) в 2019 году:

1. Алтайский край в 2019 году лидирует в рейтинге регионов России по валовым сборам чечевицы — 41,8 тыс. тонн (35,9% в общем объеме сборов). За год сборы сократились на 42,8% (на 31,3 тыс. тонн).

2. Саратовская область (сборы составили 29,4 тыс. тонн, доля в общем объеме сборов — 25,2%).

3. Омская область (11,3 тыс. тонн, 9,7%).

4. Пензенская область (5,3 тыс. тонн, 4,5%).

5. Оренбургская область (4,9 тыс. тонн, 4,2%).

6. Самарская область (3,2 тыс. тонн, 2,8%).

7. Республика Крым (2,7 тыс. тонн, 2,3%).

8. Курская область (2,7 тыс. тонн, 2,3%).

9. Ставропольский край (2,6 тыс. тонн, 2,2%).

10. Республика Башкортостан (2,6 тыс. тонн, 2,2%).

11. Волгоградская область (2,1 тыс. тонн, 1,8%).

12. Орловская область (1,9 тыс. тонн, 1,7%).

13. Новосибирская область (1,6 тыс. тонн, 1,4%).

14. Республика Татарстан (1,1 тыс. тонн, 1,0%).

15. Ростовская область (0,6 тыс. тонн, 0,5%).

16. Челябинская область (0,6 тыс. тонн, 0,5%).

17. Рязанская область (0,6 тыс. тонн, 0,5%).

18. Краснодарский край (0,5 тыс. тонн, 0,4%).

19. Ульяновская область (0,5 тыс. тонн, 0,4%).

20. Тульская область (0,3 тыс. тонн, 0,3%).

Валовые сборы чечевицы в других регионах составили 0,3 тыс. тонн (0,3% в общем объеме сборов).

Урожайность чечевицы в России в 2001-2019 гг.

Средняя урожайность чечевицы в России в 2019 году составила 9,0 ц/га убранной площади, что на 13,9% (на 1,1 ц/га) больше, чем 2018 году. За 5 лет (к 2014 году), урожайность чечевицы выросла на 13,9% (на 1,1 ц/га), за 10 лет — на 28,7% (на 2,0 ц/га), к 2001 году — на 8,4% (на 0,7 ц/га).

Анализ среднегодовых показателей за длительный период позволяет в значительной степени исключить влияние природно-климатических факторов и определить вклад использования передовых технологий в изменение урожайности чечевицы в России.

Среднегодовая урожайность чечевицы в России в 2001-2010 гг. находилась на отметках в 7,7 ц/га, в 2011-2019 гг. — возросла до 8,9 ц/га.

Урожайность чечевицы по ключевым регионам-производителям (ТОП-20 регионов-производителей) в 2019 году:

1. Алтайский край. Урожайность чечевицы в 2019 году в регионе составила 8,6 ц/га.

2. Саратовская область — 8,2 ц/га.

3. Омская область — 10,3 ц/га.

4. Пензенская область — 9,3 ц/га.

5. Оренбургская область — 9,7 ц/га.

6. Самарская область — 10,2 ц/га.

7. Республика Крым — 7,8 ц/га.

8. Курская область — 23,6 ц/га.

9. Ставропольский край — 9,0 ц/га.

10. Республика Башкортостан — 12,5 ц/га.

11. Волгоградская область — 6,6 ц/га.

12. Орловская область — 19,5 ц/га.

13. Новосибирская область — 9,6 ц/га.

14. Республика Татарстан — 9,6 ц/га.

15. Ростовская область — 6,8 ц/га.

16. Челябинская область — 6,2 ц/га.

17. Рязанская область — 14,8 ц/га.

18. Краснодарский край — 13,0 ц/га.

19. Ульяновская область — 6,9 ц/га.

20. Тульская область — 17,2 ц/га.

В других регионах РФ урожайность чечевицы составила 11,6 ц/га, в среднем по РФ — 9,0 ц/га.

Источник: Экспертно-аналитический центр агробизнеса «АБ-Центр» www.ab-centre.ru. При частичном или полном использовании материалов, активная гиперссылка на данную статью обязательна.

Источник

Загрузить PDF

Вам дана задача, в которой требуется найти площадь четырехугольника, а вы даже не знаете, что такое четырехугольник? Не волнуйтесь, эта статья вам поможет! Четырехугольник — это любая фигура с четырьмя сторонами. Для вычисления площади четырехугольника нужно определить тип четырехугольника, который вам дан, и воспользоваться соответствующей формулой.

1
Определение параллелограмма. Параллелограмм — это четырехугольник, у которого противоположные стороны равны и параллельны друг другу. Квадраты, прямоугольники и ромбы — это параллелограммы.
- Квадрат — это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
- Прямоугольник — это параллелограмм, у которого все стороны пересекаются под прямым углом.
- Ромб — это параллелограмм, у которого все стороны равны.
2
Площадь прямоугольника. Чтобы вычислить площадь прямоугольника, нужно знать его ширину (короткая сторона; представьте ее как высоту) и длину (длинная сторона; представьте ее как сторону, к которой проведена высота). Площадь прямоугольника равна произведению длины на ширину.
- ‘Площадь = длина х высота, или S = a х h.
- Пример: если длина прямоугольника равна 10 см, а ширина равна 5 см, то площадь этого прямоугольника: S = 10 х 5 = 50 квадратных сантиметров.
- Не забывайте, что площадь измеряется в квадратных единицах (квадратных метрах, квадратных сантиметрах и так далее).
3
Площадь квадрата. Квадрат — это частный случай прямоугольника, поэтому используйте ту же формулу, что и для нахождения площади прямоугольника. Но в квадрате все стороны равны, поэтому площадь квадрата равна любой из его сторон, возведенной в квадрат (то есть умноженной саму на себя).^[1]
- Площадь = сторона х сторона, или S = a².
- Пример: если сторона квадрата равна 4 см (a = 4), то площадь этого квадрата: S = a² = 4 х 4 = 16 квадратных сантиметров.
4
Площадь ромба равна произведению его диагоналей, разделенной на два. Диагонали — это отрезки, соединяющие противоположные вершины ромба.^[2]
- Площадь = (диагональ1 х диагональ2)/2, или S = (d₁ × d₂)/2
- Пример: если диагонали ромба равны 6 см и 8 см, то площадь этого ромба: S = (6 х 8)/2 = 24 квадратных сантиметров.
5
Площадь ромба также можно найти, если умножить его сторону на высоту, опущенную на эту сторону. Но не путайте высоту со смежной стороной. Высота — это прямая, опущенная из любой вершины ромба на противоположную сторону, и пересекающая противоположную сторону под прямым углом.
- Пример: если длина ромба равна 10 см, а его высота равна 3 см, то площадь такого ромба равна 10 х 3 = 30 квадратных сантиметров.
6
Формулы для вычисления площадей ромба и прямоугольника применимы к квадратам, так как квадрат — это частный случай как прямоугольника, так и ромба.
- Площадь = сторона х высоту, или S = a × h
- Площадь = (диагональ1 × диагональ2)/2, или S = (d₁ × d₂)/2
- Пример: если сторона квадрата равна 4 см, то его площадь равна 4 х 4 = 16 квадратных сантиметров.
- Пример: диагонали квадрата равны по 10 см. Вы можете найти площадь этого квадрата по формуле: (10 х 10)/2 = 100/2 = 50 квадратных сантиметров.
Реклама

1
Определение трапеции. Трапеция — это четырехугольник, у которого две противоположные стороны параллельны друг другу. Каждая из четырех сторон трапеции может быть разной длины.
- Есть два способа вычисления площади трапеции (в зависимости от данных значений).
2
Найдите высоту трапеции. Высота трапеции — отрезок, соединяющий параллельные стороны (основания) и пересекающий их под прямым углом (высота не равна боковым сторонам). Вот как найти высоту трапеции:^[3]
- Из точки пересечения меньшего основания и боковой стороны проведите перпендикуляр к большему основанию. Этот перпендикуляр и есть высота трапеции.
- Чтобы вычислить высоту, используйте тригонометрию. Например, если вы знаете боковую сторону и прилегающий к ней угол, то высота равна произведению боковой стороны на синус прилегающего угла.
3
Найдите площадь трапеции, используя высоту. Если вы знаете высоту трапеции и оба основания, используйте следующую формулу для вычисления площади трапеции:
- Площадь = (основание1 + основание2)/2 × высота, или S = (a+b)/2 × h
- Пример: если высота трапеции равна 2 см, а основания трапеции равны 7 см и 11 см, то площадь этой трапеции: S = (a+b)/2 * h = (7 + 11)/2 * 2 = 18 квадратных сантиметров.
- Если высота трапеции равна 10, а основания трапеции равны 7 и 9, то площадь этой трапеции: S = (a+b)/2 * h = (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80.
4
Найдите площадь трапеции, используя среднюю линию. Средняя линия — это отрезок, параллельный основаниям и делящий боковые стороны пополам. Средняя линия равна среднему значению от обоих оснований (a и b): средняя линия = (a+b)/2.
- Площадь = средняя линия х высота, или S = m × h
- По сути, здесь вы используете формулу для нахождения площади трапеции по двум основаниям, но вместо (a+b)/2 подставлена m (средняя линия).
- Пример: если средняя линия трапеции равна 9 см, то площадь этой трапеции: S = m*h = 9 х 2 = 18 квадратных сантиметров (вы получили тот же ответ, что и в предыдущем шаге).
Реклама

1
Определение дельтоида. Дельтоид — это четырехугольник с двумя парами сторон одинаковой длины.
- Есть два способа вычисления площади дельтоида (в зависимости от данных значений).
2
Найдите площадь дельтоида, используя формулу для нахождения площади ромба (с использованием диагоналей), так как ромб — это частный случай дельтоида, у которого все стороны равны. Напомним, что диагональ — отрезок, соединяющий противоположные вершины.
- Площадь = (диагональ1 х диагональ2)/2, или S = (d₁ × d₂)/2
- Пример: если диагонали дельтоида равны 19 см и 5 см, то площадь этого дельтоида: S = (19 х 5)/2 = 47,5 квадратных сантиметров.
- Если вы не знаете длины диагоналей и не можете их измерить, используйте тригонометрию, чтобы вычислить их. Прочтите эту статью, чтобы узнать больше информации.
3
Найдите площадь дельтоида, используя неравные стороны и угол между ними. Если вы знаете неравные стороны и угол между этими сторонами (θ), то площадь дельтоида вычисляется с помощью тригонометрии по формуле:^[4]
- Площадь = (сторона1 х сторона2) х sin (угол), или S = (a × b) × sin(θ), где θ — угол между неравными сторонами.
- Пример: Если стороны дельтоида равны 4 см и 6 см, а угол между ними равен 120 градусам, то площадь дельтоида равна (6 х 4) х sin120 = 24 х 0,866 = 20,78 квадратных сантиметров.
- Обратите внимание, что вы должны использовать две неравные стороны и угол между ними; если вы используете две равные стороны и угол между ними, вы получите неправильный ответ.
Реклама

1
Если вам дан четырехугольник произвольной формы, то даже для таких четырехугольников существуют формулы для вычисления их площадей. Обратите внимание, что такие формулы требуют знания тригонометрии.
- Во-первых, найдите длины всех четырех сторон. Обозначим их через a, b, c, d (а напротив с, а b напротив d).
- Пример: дан четырехугольник произвольной формы со сторонами 12 см, 9 см, 5 см и 14 см.
2
Найдите угол А между сторонами а и d и угол С между сторонами b и с (вы можете найти любые два противолежащих угла).
- Пример: в нашем четырехугольнике А = 80 градусов и C = 110 градусов.
3
Представьте, что существует отрезок, соединяющий вершины, образованные сторонами а и b и сторонами с и d. Этот отрезок разделит четырехугольник на два треугольника. Так как площадь треугольника равна 1/2absinC, где C — угол между сторонами a и b, вы можете найти площади двух треугольников и сложить их, чтобы вычислить площадь квадрата.
- Площадь = 0,5 х сторона1 х сторона4 х sin(угол между стороной1 и стороной4) + 0,5 х сторона2 х сторона3 х sin(угол между стороной2 и стороной3), или
- Площадь = 0,5 a × d × sin A + 0,5 × b × c × sin C
- Пример: вы нашли стороны и углы, поэтому просто подставьте их в формулу.
  
  = 0,5 (12 × 14) × sin (80) + 0,5 × (9 × 5) × sin (110)
  
  = 84 × sin (80) + 22,5 × sin (110)
  
  = 84 × 0,984 + 22,5 × 0,939
  
  = 82,66 + 21,13 = 103,79 квадратных сантиметров.
- Обратите внимание, что если вы пытаетесь найти площадь параллелограмма (у которого противоположные углы равны), то формула примет вид: площадь = 0.5*(ad + bc) * sin A
Реклама

Советы

Этот калькулятор для вычисления площади треугольника пригодится вам при вычислении площади четырехугольника произвольной формы.^[5]
Чтобы получить дополнительную информацию, прочитайте статьи по вычислению площади квадрата, площади прямоугольника, площади ромба, площади трапеции и площади дельтоида.

Об этой статье

Эту страницу просматривали 441 078 раз.

Была ли эта статья полезной?

Источник