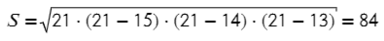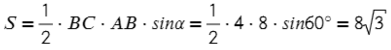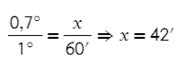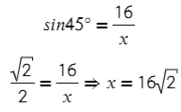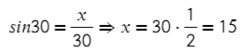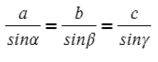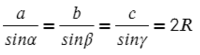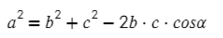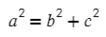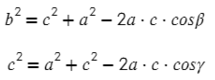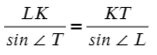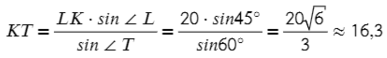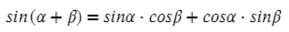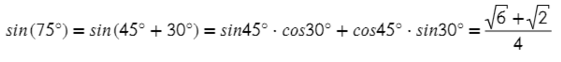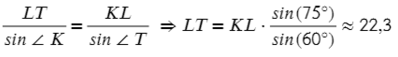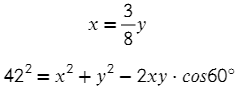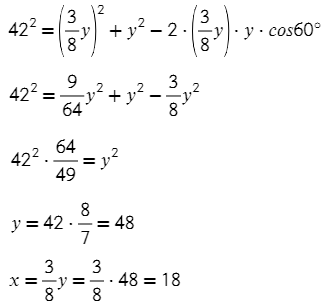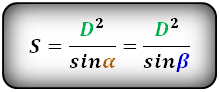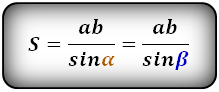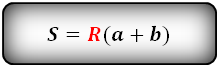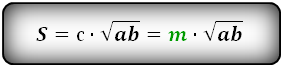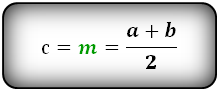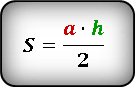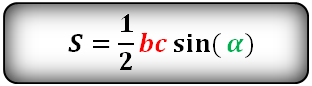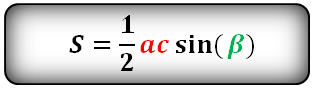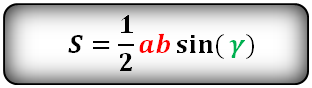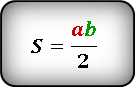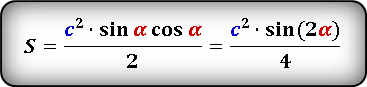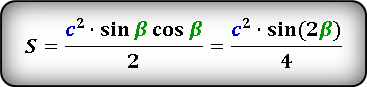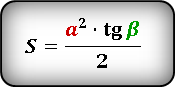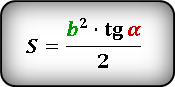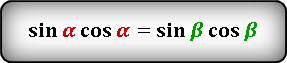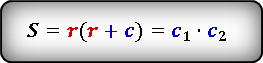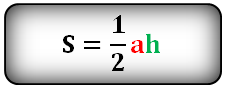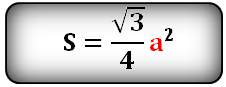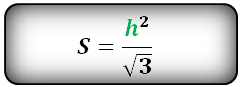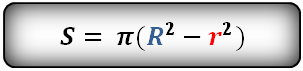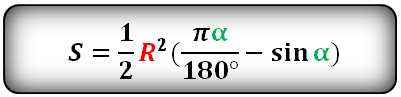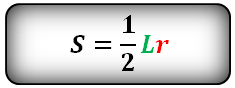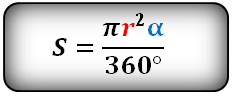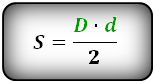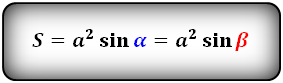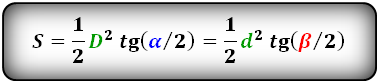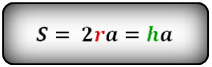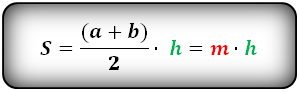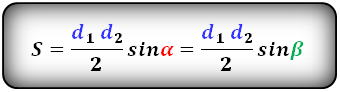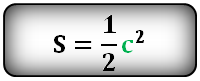Как найти площадь через синус или косинус - Исправление недочетов и поиск решений вместе с Examum.ru

I. Площадь треугольника через синус

Если в задаче даны длины двух сторон треугольника и угол между ними, то можно применить формулу площади треугольника через синус.

Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По таблице синусов синус угла в 30° равен 0.5

Площадь треугольника будет равна 3 кв. см.

Калькулятор нахождения площади треугольника через синус

Сторона a=	Сторона b=	Угол γ °
Ответ: Площадь треугольника = 3.000

Также могут быть и другие условия. Если дана длина одной стороны и углы, то для начала нужно вычислить недостающий угол. Т.к. сумма всех углов треугольника равняется 180°, то:

Площадь будет равна половине квадрата стороны, умноженной на дробь. В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:

Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол: $alpha={180^circ}-({60^circ}+{60^circ})$
Подставляем данные в формулу $S= {1/2} * {3^2} * {{ sin{60^circ} * sin{60^circ} } / { sin{60^circ} }}={1/2} * 9 * {{ 0.86 * 0.86 } / { 0.86 }}=3.87$
Получаем, что площадь треугольника равняется 3,87 кв. см.

II. Площадь треугольника через косинус

Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти не известные стороны, а уже потом использовать формулу Герона.
По теореме косинусов квадрат неизвестной стороны треугольника равняется сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла, находящегося между ними.
${c^2}={a^2}+{b^2}-2*a*b*cos{gamma}$
Из теоремы выводим формулы для поиска длины неизвестной стороны:

Зная как найти недостающую сторону, имея две стороны и угол между ними можно легко посчитать площадь. Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.

Пример расчета формулы площади треугольника через косинус
Дан треугольник с известными сторонами a = 3, b = 4, и углом γ= 45°. Для начала найдем недостающую сторону с. По таблице косинусов косинус 45°=0,7. Для этого подставим данные в уравнение, выведенное из теоремы косинусов. $c=sqrt{ {3^2}+{4^2}-2*3*4*cos{45^circ} }=sqrt{ 9+16-2*3*4*0.7 }=sqrt{ 25-16.97 }=2.83$
Теперь используя формулу, найдем площадь треугольника по трем сторонам:

Калькулятор нахождения площади треугольника через косинус

Сторона a=	Сторона b=	Угол γ °
Ответ: Площадь треугольника = 4.243

Источник

Формулы площади треугольника

Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
Формула площади треугольника по трем сторонам

Формула Герона

S = √

p

(

p — a

)(

p — b

)(

p — c

)
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон, умноженного на синус угла между ними.
Формула площади треугольника по трем сторонам и радиусу описанной окружности
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

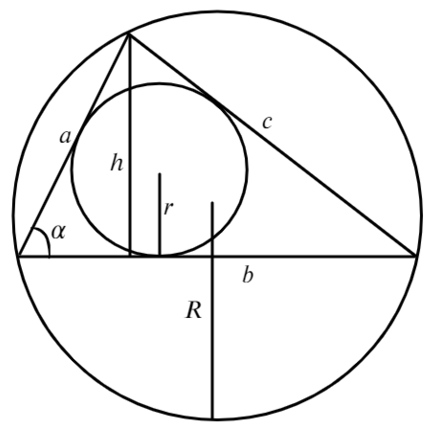
где S — площадь треугольника,

a, b, c

— длины сторон треугольника,

— высота треугольника,

— угол между сторонами

— радиус вписанной окружности,
R — радиус описанной окружности,

— полупериметр треугольника.

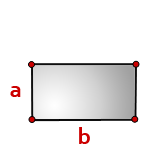
Формула площади прямоугольника

Площадь прямоугольника

где S — Площадь прямоугольника,

a, b

— длины сторон прямоугольника.

Формулы площади параллелограмма

Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
Формула площади параллелограмма по диагоналям и углу между ними Площадь параллелограмма равна половине произведения длин его диагоналей, умноженному на синус угла между ними.
S = 1/2
d1 · d2 · sin

γ
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон, умноженному на синус угла между ними.

где S — Площадь параллелограмма,

a, b

— длины сторон параллелограмма,

— длина высоты параллелограмма,

— угол между сторонами параллелограмма,

γ —

угол между диагоналями параллелограмма,

d1, d2 — длины диагоналей параллелограмма.

Формулы площади ромба

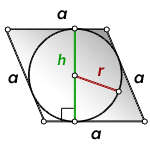
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.

где S — Площадь ромба,

— длина стороны ромба,

— длина высоты ромба,

— угол между сторонами ромба,

₁,

₂ — длины диагоналей.

Формулы площади трапеции

Формула Герона для трапеции

S =
a

+

b
√(

p — a

)(

p — b

)(

p — a — c

)(

p — a — d

)

4|

a

—

b

|
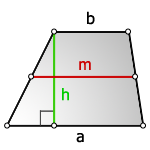
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высоту
где S — Площадь трапеции,
a, b

— длины основ трапеции,

c, d

— длины боковых сторон трапеции,

p

=

a

+

b

+

c

+

d
— полупериметр трапеции.

2

Источник

Площадь треугольников.

Свойства треугольников.

Тригонометрия в прямоугольных треугольниках.

Что такое синус/косинус.

Таблицы Брадиса. Как пользоваться.

Теорема синусов и косинусов.

Геометрия — это искусство хорошо рассуждать на плохо выполненных чертежах.

Г. Абель

С основными свойствами разобрались, теперь рассмотрим формулы и их приминение.

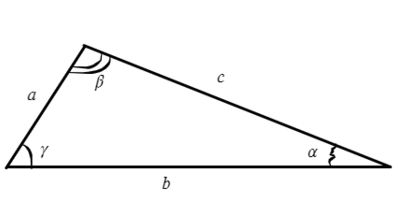
Площадь произвольного треугольника

Нет, это не кривая пентаграмма, нужны на этом рисунке только обозначения. Рассмотрим формулы школьной программы.

Высоту умножаем на ту сторону, на которую приходит высота:
В эту формулу подставляем угол между сторонами a и b:

Удобно использовать эту формулу, когда известны все стороны треугольника, p — полупериметр (половина суммы длин всех сторон):

Данная формула отлично помогает найти радиус вписанной окружности для любого треугольника, если известна площадь:

А эта формула помогает найти радиус описанной окружности для любого треугольника:

А зачем такое количество формул? К каждой задаче будут предоставлять разное дано, удобно знать и применять все формулы, чтобы максимально быстро решать задачи.

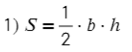
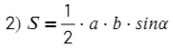
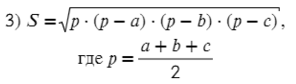
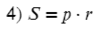
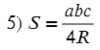
Полезные формулы для прямоугольного и равностороннего треугольника:

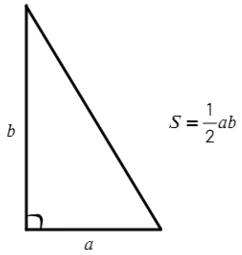
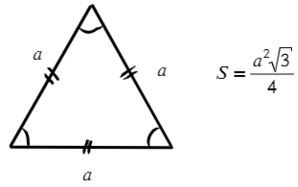
В данном случае получается, что один катет «b» — высота треугольника, а катет «а» — основание.

Эту формулу можно вывести большим количеством способов, самый простой через формулу №2

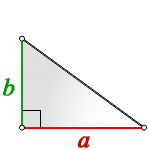
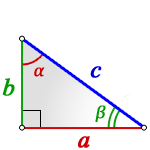
Задача №1. Дано на рисунке:

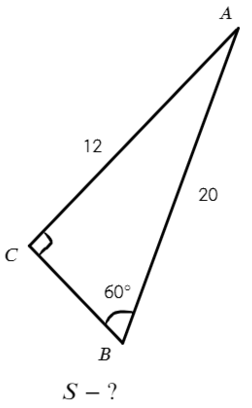
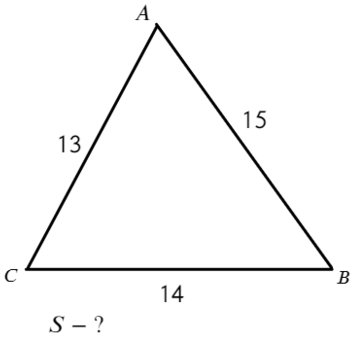
Оттолкнемся от вопроса: нужно найти площадь. Помимо 5 формул для произвольного треугольника, нам подойдет формула нахождения площади через полупроизведение катетов.

Вариантов здесь много (можно через т. Пифагора), но самый быстрый — найти ∠А = 180°− 90° − 60° = 30°, тогда площадь найдем по (2) формуле: S = ½absinα

Ответ: 60

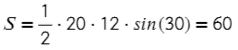
Задача №2. Дано на рисунке:

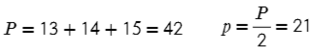
Снова оттолкнемся от вопроса: нужно найти площадь. Дан обычный треугольник, значит, наш выбор ограничен первыми 5−ью формулами. В первой нужна высота, во второй угол, а в третьей полупериметр, но мы же знаем все стороны! Для начала найдем периметр и полупериметр:

Теперь можно подставить все числа в формулу площади:

Главное — правильно определиться с формулой.

Ответ: 84

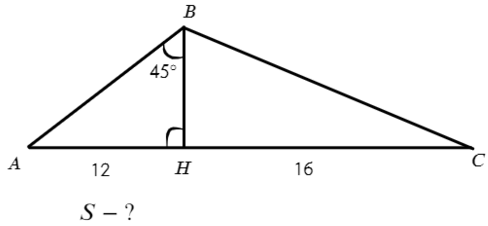
Задача №3. Дано на рисунке:

В ΔABH: ∠A = 180°− 90° − 45° = 45°, значит, ∠A = ∠B => BH = AH = 12.

Тогда площадь можно найти по формуле (1) S=½bh. Высота AH = 12, основание AC = 16+12 = 28. => S = ½×12×28 = 168

Ответ: 168.

Задача №4. Дано на рисунке:

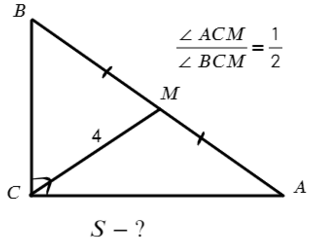
Оттолкнемся от отношения, которое нам дано. Мы знаем, что сумма данных углов равна 90°, если ∠ACM = х и ∠ВCM = 2х, тогда 2х+х = 90°

∠ACM = х = 30° => ∠ВCM = 60°. А что у нас равно 4-ем? Да, медиана! А медиана, проведенная из прямого угла, равна половине гипотенузы (2−ое свойство). Тогда отметим равные углы:

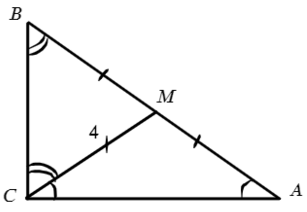
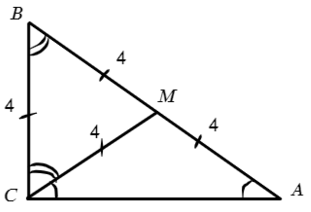
В ΔBCM получается ∠ВCM = ∠СВM = 60°, тогда ∠СМВ = 60° и ΔBCM — правильный:

Площадь найдем по (2) формуле: S = ½absinα:

Ответ: 8√3

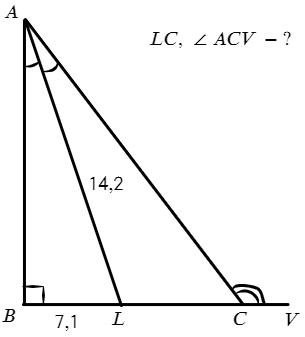
Задача №5. Дано на рисунке:

В дано есть только стороны, а найти нужно угол. Как это сделать? Вот стороны 14,2 и 7,1 во сколько раз отличаются? Да, в 2 раза, а значит угол ∠BAL = 30° (против угла в 30° лежит катет, который в два раза меньше гипотенузы).

Значит, ∠A = 60° => ∠ACB = 180° − 90° − 60° = 30°, а ∠ACB — смежный с ∠ACV => ∠ACV = 180° − 30° = 150°.

Что касается LC: внимательно рассмотрим ΔALC, можно даже лупой воспользоваться. Что видишь? ∠LAC = ∠ACL = 30° => ΔALC — равнобедренный, LC = AL = 14,2.

Ответ: 14,2 и 150°

Тригонометрия в прямоугольных треугольниках

В прямоугольном треугольнике три стороны: 2 катета и гипотенуза.

Катеты меньшие стороны треугольника. Гипотенуза большая сторона, которая лежит напротив угла в 90°.

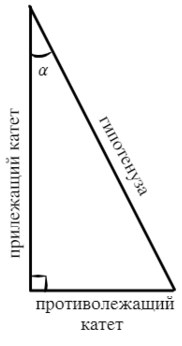
Относительно угла α:

Катет, который составляет угол, называют прилежащим. Катет, который находится напротив угла, называют противолежащим. Логично? Замечательно!

Тригонометрические функции (синус, косинус…) задают связь между углом и длинами сторон.

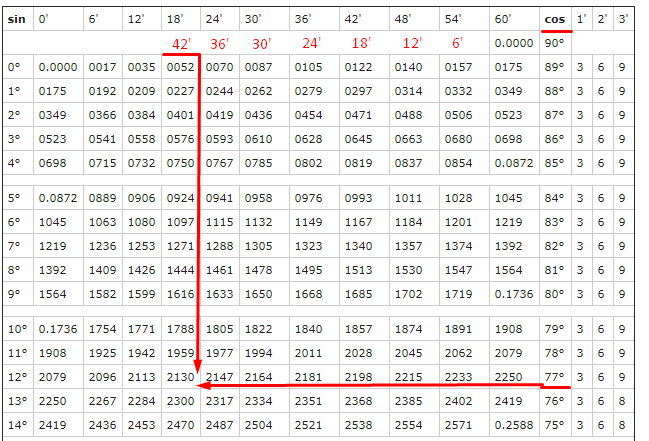
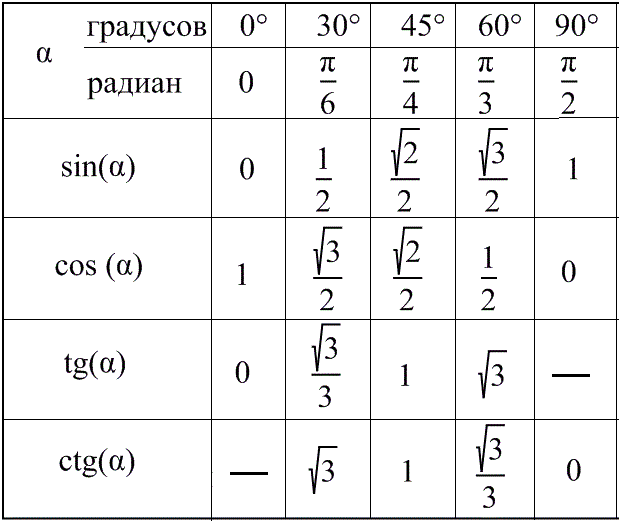
Но хорошо бы знать какие-то значения тригонометрических функций при определенных углах. Все значения вместе образуют таблицу Брадиса. С ее помощью можно вычислить почти любое значение тригонометрической функции при заданом угле. Но как с ней работать?

Найдем sin(10°). Для этого выберем столбец sin и в нем найдем 10°. Ближайшее значение — это то, что нам нужно — 0,1736.

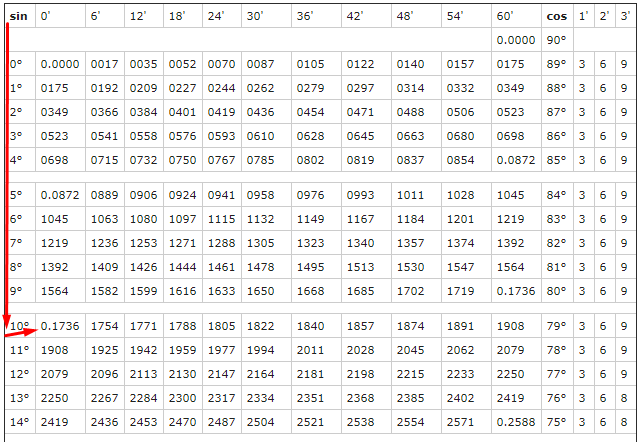
А что за столбец 0′; 6′; 12′ и т.д. Это минуты! Не те, которых мы ждем в конце урока, а градусные минуты.

Из общего: и те, и другие минуты измеряются в промежутке от 0 до 60.

Градусные минуты делят один градус на 60 минут (1°=60′), нужны они для большей точности задания угла.

p.s. Есть еще и градусные секунды, и в одной градусной минуте 60 градусных секунд, знакомо? 1° = 60′ = 3600».

Найдем cos(77,7°)

Семь десятых градуса нужно перевести в минуты. Можно через пропорцию:

Теперь в таблице нужно найти 77°42′ для косинуса. Для синуса минуты прописаны, а для косинуса нет. Но мы же люди не гордые, сами напишем, но в обратном порядке. На пересечении 77° и 42′ получаем наше значение:

Но чтобы не загромождать таблицу 0, его в начале пишут только в первых строчках, поэтому ответ cos(77,7°) = 0,213.

В задачах же таким обилием углов похвастаться нельзя, достаточно знать значения для 30°; 45°; 60°; 90°.

Искусство решать геометрические задачи чем-то напоминает трюки иллюзионистов — иногда,

даже зная решение задачи, трудно понять, как можно было до него додуматься.

И.Д. Новиков

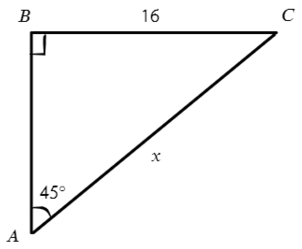
Задача №6. Дано на рисунке:

В этой задаче известен противолежащий катет относительно угла в 45°, а найти нужно гипотенузу. Смотрим, где у нас есть противполежащий катет и гипотенуза? Это синус!

Смотрим в таблице, чему равен синус 45°, и подставляем в отношение:

Ответ: 16√2

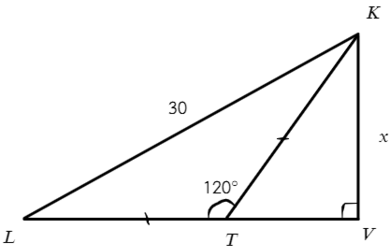
Задача №7. Дано на рисунке:

Мы разобрались с тригонометрическими функциями в прямоугольных треугольниках, значит, и в этой задаче нужно перейти к прямоугольному треугольнику.

В ΔLTK — равнобедренный : ∠L = ∠LKT = (180° − 120°)/2 = 30°

Отлично, в прямоугольном ΔLVK: ∠L = 30° и известна гипотенуза, а нам нужно найти противолежащий катет, чем воспользуемся? Опять синусом!

Ответ: 15

Теорема синусов и теорема косинусов

Сразу возникает вопрос, а теорема тангенсов тоже есть? Конечно, есть, но она очень редко используется.

Для любого треугольника можно записать такое соотношение, это будет теорема синусов:

Запомни, что сторона относится к синусу противолежащего угла.

Следствие из теорма синусов гласит, что любое соотношение равно двум радиусам описанной окружности:

Для любого треугольника можно записать такое соотношение, это будет теорема косинусов:

А что будет, если α = 90°, а cos(90) = 0? Получится:

Теорема Пифагора, вот так просто можно запомнить теорему косинусов. Начать как теорему Пифагора, а затем вычесть удвоенное произведение на косинус угла между ними.

Можно записать и для других сторон в этом же треугольнике:

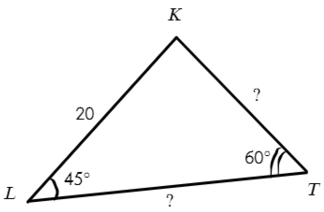
Задача №8. Дано на рисунке:

Запишем теорему синусов для двух отношений:

Выразим отсюда KT:

∠K = 180° − 60° − 45° = 75°. Чтобы найти синус угла 75°, советую посмотреть эту статью, нужно воспользовать формулой суммы синусов:

Тогда представим 75° в виде двух табличных значений:

Аналогично выразим LT:

Ответ: 16,3 и 22,3

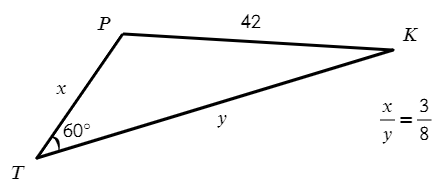
Задача №9. Дано на рисунке:

Найти нужно x и y. Запишем теорему косинусов для этого треугольника:

Икс выразим через игрек:

Ответ: 48; 18

Отлично, поздравляю тебя с Elementary по геометрии!

Что нужно знать:

Вертикальные, смежные, соответственные, накрест лежащие углы.
Равенство и подобие треугольников.
Что такое медиана, биссектриса, высота.
Свойства треугольников.
Площадь треугольников.
Синус/косинус в треугольнике.
Теорему синусов и косинусов.

Задачи для закрепления по треугольникам

Нашел опечатку, или что-то непонятно — напиши.

Группа с полезной информацией и легким математическим юмором.

Источник

Математика

Тема 6: Соотношения между сторонами и углами треугольника. Скалярное произведение векторов

Урок 2: Теорема о площади треугольника. Теорема синусов. Теорема косинусов

Видео
Тренажер
Теория

Заметили ошибку?

Тема 31.

Терема о площади треугольника. Теорема синусов. Теорема косинусов.

Теорема

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Доказательство

Пусть в треугольнике АВС

АВ=c, ВС=a, СА=b

S — площадь треугольника.

Докажем, что S=12absin⁡C

Введем систему координат с началом в точке C так, чтобы точка В лежала на положительной полуоси Cx, а точка А имела положительную ординату. Площадь данного треугольника можно вычислить по формуле S=12ah, где h — высота треугольника. Но h равна ординате точки А, то есть h = b sin⁡ C. Следовательно, S=12absin⁡C

Теорема

Стороны треугольника пропорциональны синусам противолежащих углов.

Доказательство

Пусть в треугольнике АВС

АВ = c, ВС = a, СА = b

Докажем, что

asin⁡A=bsin⁡B=csin⁡C

По теореме о площади треугольника

S=12absin⁡C,S=12bcsin⁡A, S=12acsin⁡B

Из первых двух равенств получим

12absin⁡C = 12bcsin⁡A, откуда

asin⁡A=csin⁡C

Аналогично, asinA=bsinB

Итак, asin⁡A=bsin⁡B=csin⁡C

Заметим, что отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности. Следовательно, для любого треугольника АВС со сторонами АВ = с, ВС = а, СА = bимеют место равенства

asin⁡A=bsin⁡B=csin⁡C=2R

где R — радиус описанной окружности.

Теорема

Квадрат стороны треугольника равен сумме квадратов других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Доказательство

Пусть в треугольнике АВС

АВ = c, ВС = a, СА = b

Докажем, например, что

a² = b² + c² — 2bc cos⁡ A

Введем систему координат с началом в точке A так, как показано на рисунке. Тогда точка В имеет координаты (c;0), а точка С имеет координаты b cos⁡ A; b sin⁡ A. По формуле расстояния между двумя точками, получим:

BC2=a2=bcos⁡A-c2+b2sin2A

a2=b2cos2A+b2sin2A-2bccos⁡A+c2

a2=b2cos2A+sin2A-2bccos⁡A+c2

a2=b2+c2-2bccos⁡A

Найти площадь ∆ABC, если BC = 3 см, AB=182 см, ∠B = 45°.

По теореме о площади треугольника

S=12BC∙AB∙sin⁡B

S=12∙3∙182∙sin⁡45°

S=12∙3∙182∙22

S = 27 см²

Ответ: 27 см²

Заметили ошибку?

Расскажите нам об ошибке, и мы ее исправим.

Источник

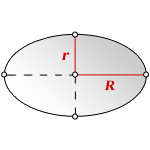
R — большая полуось

r — малая полуось

π ≈ 3.14

Формула площади эллипса, через полуоси:

Калькулятор, вычислить площадь элипса:

1. Формула площади равнобедренной трапеции через стороны и угол

а — нижнее основание

b — верхнее основание

с — равные боковые стороны

α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S ):

Формула площади равнобедренной трапеции через стороны и угол, (S ):

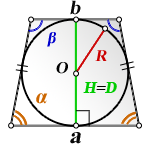
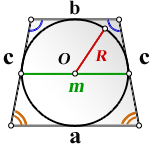
2. Формулы площади равнобедренной трапеции если в нее вписана окружность

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α, β — углы трапеции

а — нижнее основание

b — верхнее основание

Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):

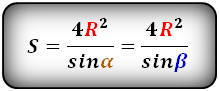
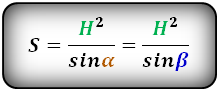
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

R — радиус вписанной окружности

m — средняя линия

O — центр вписанной окружности

c — боковые стороны

а — нижнее основание

b — верхнее основание

Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию (S ):

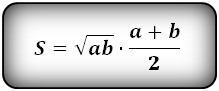
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α, β — углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

c — боковая сторона

m — средняя линия трапеции

α, β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

a — нижнее основание

b — верхнее основание

h — высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S ):

Треугольник это плоская фигура, которая имеет три стороны и три угла. Сумма всех трех углов, равна 180 градусов.
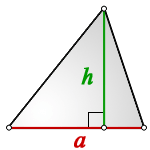
Высота треугольника это — опущенный перпендикуляр из вершины угла на противоположенную сторону или ее продолжение, которую в этом случае, называют основанием.

Что бы найти площадь треугольника,

для этого надо основание умножить на высоту и разделить на два

1. Площадь разностороннего треугольника

h — высота треугольника

a — основание

Формула площади треугольника (S):

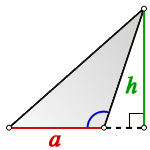
2. Площадь треугольника с тупым углом

h — высота треугольника

a — основание

Формула площади треугольника с тупым углом (S):

Формулы для треугольника:

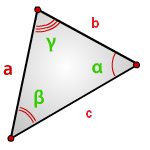
Зная у треугольника

две стороны и синус угла между ними, находим по формуле, его площадь

a, b, c — стороны треугольника

α, β, γ — углы

Формулы площади треугольника, через две стороны и угол между ними, (S):

Калькулятор — вычислить, найти площадь треугольника:

Формулы для треугольника:

Сторона произвольного треугольника

Стороны равнобедренного треугольника

Стороны прямоугольного треугольника

Высота произвольного треугольника

Высота прямоугольного треугольника

Высота, медиана, биссектриса равнобедренного треугольника

Высота=медиана=биссектриса равностороннего треугольника

Биссектриса произвольного треугольника

Биссектриса прямоугольного треугольника

Медиана произвольного треугольника

Медиана прямоугольного треугольника

Все разделы по геометрии

Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется — гипотенуза

1. Если известны только катеты

a, b — катеты треугольника

Формула площади треугольника через катеты ( S ) :

2. Если известны острый угол и гипотенуза или катет

c — гипотенуза

a, b — катеты

α, β — острые углы

Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :

Формулы площади прямоугольного треугольника через катет и угол ( S ) :

Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если

то справедливы следующие тождества:

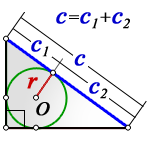
3. Если известны радиус вписанной окружности и гипотенуза

c — гипотенуза

c₁, c₂ — отрезки полученные делением гипотенузы, точкой касания окружности

r — радиус вписанной окружности

О — центр вписанной окружности

Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :

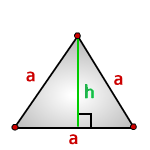
Если вы знаете сторону или высоту

вы можете найти площадь равностороннего треугольника

a — сторона треугольника

h — высота

Площадь треугольника через сторону a и высоту h, (S):

Площадь треугольника только через сторону a, (S):

Калькулятор для расчета площади равностороннего треугольника

Площадь треугольника только через высоту h, (S):

Калькулятор для расчета площади равностороннего треугольника

a — сторона треугольника

h — высота

Формулы для треугольника:

Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).
Радиус круга — отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга — отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса

Зная диаметр

или радиус круга или длину окружности, можно найти его площадь.

r — радиус круга

D — диаметр круга

π ≈ 3.14

Формула площади круга, (S):

Решения задач

на тему: Площадь круга

Калькулятор для расчета площади круга через радиус

Калькулятор для расчета площади круга через диаметр

L — длина окружности

О — центр круга

π ≈ 3.14

Формула площади круга если известна длина окружности, (S):

Решения задач

на тему: Площадь круга

Калькулятор для расчета площади круга через длину

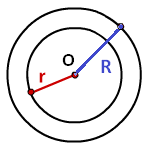
Площадь кольца равна — число π, умноженное на разницу квадратов, радиуса внешней окружности и радиуса внутренней окружности

R — радиус внешней окружности

r — радиус внутренней окружности

π ≈ 3.14

Формула площади кольца (S):

Калькулятор — вычислить, найти площадь кольца

R — радиус внешней окружности

r — радиус внутренней окружности

α — угол сектора AOB, в градусах

π ≈ 3.14

Формула площади сектора кольца (S):

R — радиус круга

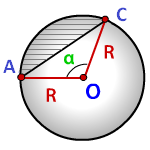
α — угол сегмента в градусах

π ≈ 3.14

Формула площади сегмента круга (S), отсекаемая хордой AC:

Калькулятор для расчета длины дуги окружности :

Формулы для окружности и круга:

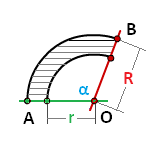
Найти площадь сектора круга если даны радиус и длина дуги или радиус и центральный угол

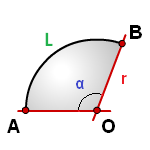
r — радиус круга

L — длина дуги AB

α — угол сектора круга AOB в градусах

π ≈ 3.14

Формула площади сектора круга (S), через длину дуги (L):

Формула площади сектора круга (S), через угол (α):

Формулы для окружности и круга:

Вычислить площадь ромба, зная: (диагонали) или (сторону и угол между ними) или (диагональ и угол между сторонами)

a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

β — тупой угол

Формулы площади ромба через диагонали и углы между сторонами ( S ):

a — сторона ромба

h — высота

r — радиус вписанной окружности

Формула площади ромба через высоту или радиус вписанной окружности ( S ):

1. Формула площади трапеции через основания и высоту

a — нижнее основание

b — верхнее основание

m — средняя линия

h — высота трапеции

Формула площади трапеции, (S ):

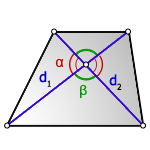
2. Формула площади трапеции через диагонали и угол между ними

d₁, d₂ — диагонали трапеции

α, β — углы между диагоналями

Формула площади трапеции, (S ):

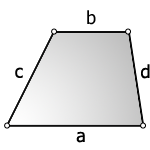
3. Формула площади трапеции через четыре стороны

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

Формула площади трапеции, (S ):

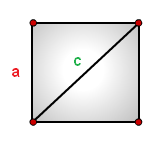
Зная сторону

или диагональ квадрата, можно найти его площадь

a — сторона квадрата

c — диагональ

Формула площади квадрата через сторону a, (S):

Калькулятор — вычислить, найти площадь квадрата:

Формула площади квадрата через диагональ c, (S):

Зная длину

и ширину прямоугольника, можно вычислить его площадь

b — длина прямоугольника

a — ширина прямоугольника

Формула площади прямоугольника, (S):

Калькулятор — вычислить, найти площадь прямоугольника:

a — сторона многоугольника

n — количество сторон

Формула площади правильного многоугольника, (S):

Калькулятор — вычислить, найти площадь правильного многоугольника

Источник

I. Площадь треугольника через синус

II. Площадь треугольника через косинус

Формулы площади треугольника

Формула Герона

Формула площади прямоугольника

Формулы площади параллелограмма

Формулы площади ромба

Формулы площади трапеции

Площадь произвольного треугольника

Тригонометрия в прямоугольных треугольниках

Теорема синусов и теорема косинусов

Что нужно знать:

Задачи для закрепления по треугольникам

Нашел опечатку, или что-то непонятно — напиши.

Группа с полезной информацией и легким математическим юмором.

Математика

Урок 2: Теорема о площади треугольника. Теорема синусов. Теорема косинусов

Заметили ошибку?

1. Площадь разностороннего треугольника

2. Площадь треугольника с тупым углом