Как найти площадь четырехугольника 4 класс впр - Исправление недочетов и поиск решений вместе с Examum.ru

Альфашкола
Уроки по математике
Готовимся к ВПР
ВПР 4 класс: нахождение периметра и площади фигур

ВПР 4 класс: нахождение периметра и площади фигур — онлайн урок

К сожалению, информация по данному уроку пока отсутствует.

ВПР 4 класс: нахождение периметра и площади фигур

Давай повторим определения, которые ты уже знаешь и которые мы будем использовать в нашем уроке.

Прямоугольник – это четырехугольник, у которого равны все углы. Они также являются прямыми и составляют 90°.

Квадрат – это четырёхугольник, у которого равны все углы и стороны.

Периметр – это сумма длин всех сторон многоугольника. Общепринятое обозначение – заглавная латинская буква P.

Чтобы найти площадь прямоугольника надо его длину умножить на ширину.

Теперь установи соответствие между картинкой и правильным ответом.

Для продолжения урока кликните на кнопку ниже:

Отзывы:

Спасибо! Ребенок занимался с интересом!

Спасибо за урок !любые сложные задания больше не пугают меня

прекрасно объяснила задания и указала верный путь решения столь поистине трудных задач.

Похожие уроки

Источник

Формулы вычисления площади произвольного четырёхугольника

В школьных математических заданиях часто требуется определить площадь четырёхугольника. Все довольно просто, если задан частный случай фигуры — квадрат, ромб, прямоугольник, трапеция, параллелограмм, ромбоид. В случае же произвольного четырёхугольника все несколько сложнее, но также вполне доступно для среднего школьника. Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры.

Определения и соглашения

В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.

Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
Угол между сторонами a и b будем обозначать следующей записью (a,b).

Нахождение площади четырёхугольника различными способами и методами

Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).

Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.

Теперь пусть даны стороны и противолежащие углы четырёхугольника.

Пусть a, b, c, d известные стороны многоугольника; p — его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).

На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.

Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.

Подставим полученные данные в нашу формулу, получим: S = rad((40 — 18)*(40 — 23)*(40 — 22)*(40 — 17) — 18*23*22*17*0,97) = rad(22*17*18*23 — 18*23*22*17*1/4) = rad((22*17*18*23*(1 — 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.

Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.

Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:

Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:

S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.

Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.

Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:

S = rad((65 — 26)*(65 — 35)*(65 — 39)*(65 — 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.

Заключение

Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов — квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:

S = 1/2*d1*d2*sin(d1,d2);
S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
S = ((a + b+ c + d)/2)*r

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра.

Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.

Видео

Разобраться в этой теме вам поможет видео.

Калькулятор расчета площади четырехугольника

В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.

Расчет площади

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.

1. Через диагонали и угол между ними

Формула расчета

2. По всем сторонам (формула Брахмагупты)

Примечание: Если вокруг четырехугольника можно описать окружность.

Формула расчета

p – полупериметр четырехугольника, равняется:

Площади четырехугольников

В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:

которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.

Формулы для площадей четырехугольников

a и b – смежные стороны

d – диагональ,
φ – любой из четырёх углов между диагоналями

Получается из верхней формулы подстановкой d=2R

R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

a – сторона,
h_a – высота, опущенная на эту сторону

a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

a – сторона,
h_a – высота, опущенная на эту сторону

a – сторона,
φ – любой из четырёх углов ромба

r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

a и b – основания,
h – высота

φ – любой из четырёх углов между ними

a и b – основания,
c и d – боковые стороны

a и b – неравные стороны,
φ – угол между ними

a и b – неравные стороны,
φ₁ – угол между сторонами, равными a ,
φ₂ – угол между сторонами, равными b .

a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,

Формулу называют «Формула Брахмагупты»

Четырехугольник	Рисунок	Формула площади	Обозначения
Прямоугольник		S = ab


Параллелограмм


Квадрат		S = a 2
	S = 4r 2


Ромб




Трапеция
	S = m h


Дельтоид		S = ab sin φ



Произвольный выпуклый четырёхугольник
Вписанный четырёхугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Получается из верхней формулы подстановкой d = 2R

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Прямоугольник



Параллелограмм



Квадрат
	S = a 2 где a – сторона квадрата
	S = 4r 2


Ромб





Трапеция




Дельтоид

	где a и b – неравные стороны, φ₁ – угол между сторонами, равными a , φ₂ – угол между сторонами, равными b .


Произвольный выпуклый четырёхугольник

Вписанный четырёхугольник

Прямоугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

Параллелограмм

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Квадрат

где
a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

Ромб

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

Трапеция

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны ,

Дельтоид

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
φ₁ – угол между сторонами, равными a ,
φ₂ – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности

Произвольный выпуклый четырёхугольник

φ – любой из четырёх углов между ними

Вписанный четырёхугольник

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Вывод формул для площадей четырехугольников

Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле

Доказательство . В соответствии с рисунком 1 справедливо равенство:

что и требовалось доказать.

Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле

где a – сторона параллелограмма, а h_a – высота высота высота , опущенная на эту сторону (рис. 2).

Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

что и требовалось доказать.

Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

то, в силу утверждения 2, справедлива формула

что и требовалось доказать.

Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).

что и требовалось доказать.

Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).

Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому

что и требовалось доказать.

Утверждение 6 . Площадь трапеции трапеции можно найти по формуле

где a и b – основания, а c и d – боковые стороны трапеции ,

(рис.6).

Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.

Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:

где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).

Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.

Если r – радиус вписанной в дельтоид окружности, то

источники:

Калькулятор расчета площади четырехугольника

http://www.resolventa.ru/spr/planimetry/sqf.htm

Источник

Загрузить PDF

Вам дана задача, в которой требуется найти площадь четырехугольника, а вы даже не знаете, что такое четырехугольник? Не волнуйтесь, эта статья вам поможет! Четырехугольник — это любая фигура с четырьмя сторонами. Для вычисления площади четырехугольника нужно определить тип четырехугольника, который вам дан, и воспользоваться соответствующей формулой.

1
Определение параллелограмма. Параллелограмм — это четырехугольник, у которого противоположные стороны равны и параллельны друг другу. Квадраты, прямоугольники и ромбы — это параллелограммы.
- Квадрат — это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
- Прямоугольник — это параллелограмм, у которого все стороны пересекаются под прямым углом.
- Ромб — это параллелограмм, у которого все стороны равны.
2
Площадь прямоугольника. Чтобы вычислить площадь прямоугольника, нужно знать его ширину (короткая сторона; представьте ее как высоту) и длину (длинная сторона; представьте ее как сторону, к которой проведена высота). Площадь прямоугольника равна произведению длины на ширину.
- ‘Площадь = длина х высота, или S = a х h.
- Пример: если длина прямоугольника равна 10 см, а ширина равна 5 см, то площадь этого прямоугольника: S = 10 х 5 = 50 квадратных сантиметров.
- Не забывайте, что площадь измеряется в квадратных единицах (квадратных метрах, квадратных сантиметрах и так далее).
3
Площадь квадрата. Квадрат — это частный случай прямоугольника, поэтому используйте ту же формулу, что и для нахождения площади прямоугольника. Но в квадрате все стороны равны, поэтому площадь квадрата равна любой из его сторон, возведенной в квадрат (то есть умноженной саму на себя).^[1]
- Площадь = сторона х сторона, или S = a².
- Пример: если сторона квадрата равна 4 см (a = 4), то площадь этого квадрата: S = a² = 4 х 4 = 16 квадратных сантиметров.
4
Площадь ромба равна произведению его диагоналей, разделенной на два. Диагонали — это отрезки, соединяющие противоположные вершины ромба.^[2]
- Площадь = (диагональ1 х диагональ2)/2, или S = (d₁ × d₂)/2
- Пример: если диагонали ромба равны 6 см и 8 см, то площадь этого ромба: S = (6 х 8)/2 = 24 квадратных сантиметров.
5
Площадь ромба также можно найти, если умножить его сторону на высоту, опущенную на эту сторону. Но не путайте высоту со смежной стороной. Высота — это прямая, опущенная из любой вершины ромба на противоположную сторону, и пересекающая противоположную сторону под прямым углом.
- Пример: если длина ромба равна 10 см, а его высота равна 3 см, то площадь такого ромба равна 10 х 3 = 30 квадратных сантиметров.
6
Формулы для вычисления площадей ромба и прямоугольника применимы к квадратам, так как квадрат — это частный случай как прямоугольника, так и ромба.
- Площадь = сторона х высоту, или S = a × h
- Площадь = (диагональ1 × диагональ2)/2, или S = (d₁ × d₂)/2
- Пример: если сторона квадрата равна 4 см, то его площадь равна 4 х 4 = 16 квадратных сантиметров.
- Пример: диагонали квадрата равны по 10 см. Вы можете найти площадь этого квадрата по формуле: (10 х 10)/2 = 100/2 = 50 квадратных сантиметров.
Реклама

1
Определение трапеции. Трапеция — это четырехугольник, у которого две противоположные стороны параллельны друг другу. Каждая из четырех сторон трапеции может быть разной длины.
- Есть два способа вычисления площади трапеции (в зависимости от данных значений).
2
Найдите высоту трапеции. Высота трапеции — отрезок, соединяющий параллельные стороны (основания) и пересекающий их под прямым углом (высота не равна боковым сторонам). Вот как найти высоту трапеции:^[3]
- Из точки пересечения меньшего основания и боковой стороны проведите перпендикуляр к большему основанию. Этот перпендикуляр и есть высота трапеции.
- Чтобы вычислить высоту, используйте тригонометрию. Например, если вы знаете боковую сторону и прилегающий к ней угол, то высота равна произведению боковой стороны на синус прилегающего угла.
3
Найдите площадь трапеции, используя высоту. Если вы знаете высоту трапеции и оба основания, используйте следующую формулу для вычисления площади трапеции:
- Площадь = (основание1 + основание2)/2 × высота, или S = (a+b)/2 × h
- Пример: если высота трапеции равна 2 см, а основания трапеции равны 7 см и 11 см, то площадь этой трапеции: S = (a+b)/2 * h = (7 + 11)/2 * 2 = 18 квадратных сантиметров.
- Если высота трапеции равна 10, а основания трапеции равны 7 и 9, то площадь этой трапеции: S = (a+b)/2 * h = (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80.
4
Найдите площадь трапеции, используя среднюю линию. Средняя линия — это отрезок, параллельный основаниям и делящий боковые стороны пополам. Средняя линия равна среднему значению от обоих оснований (a и b): средняя линия = (a+b)/2.
- Площадь = средняя линия х высота, или S = m × h
- По сути, здесь вы используете формулу для нахождения площади трапеции по двум основаниям, но вместо (a+b)/2 подставлена m (средняя линия).
- Пример: если средняя линия трапеции равна 9 см, то площадь этой трапеции: S = m*h = 9 х 2 = 18 квадратных сантиметров (вы получили тот же ответ, что и в предыдущем шаге).
Реклама

1
Определение дельтоида. Дельтоид — это четырехугольник с двумя парами сторон одинаковой длины.
- Есть два способа вычисления площади дельтоида (в зависимости от данных значений).
2
Найдите площадь дельтоида, используя формулу для нахождения площади ромба (с использованием диагоналей), так как ромб — это частный случай дельтоида, у которого все стороны равны. Напомним, что диагональ — отрезок, соединяющий противоположные вершины.
- Площадь = (диагональ1 х диагональ2)/2, или S = (d₁ × d₂)/2
- Пример: если диагонали дельтоида равны 19 см и 5 см, то площадь этого дельтоида: S = (19 х 5)/2 = 47,5 квадратных сантиметров.
- Если вы не знаете длины диагоналей и не можете их измерить, используйте тригонометрию, чтобы вычислить их. Прочтите эту статью, чтобы узнать больше информации.
3
Найдите площадь дельтоида, используя неравные стороны и угол между ними. Если вы знаете неравные стороны и угол между этими сторонами (θ), то площадь дельтоида вычисляется с помощью тригонометрии по формуле:^[4]
- Площадь = (сторона1 х сторона2) х sin (угол), или S = (a × b) × sin(θ), где θ — угол между неравными сторонами.
- Пример: Если стороны дельтоида равны 4 см и 6 см, а угол между ними равен 120 градусам, то площадь дельтоида равна (6 х 4) х sin120 = 24 х 0,866 = 20,78 квадратных сантиметров.
- Обратите внимание, что вы должны использовать две неравные стороны и угол между ними; если вы используете две равные стороны и угол между ними, вы получите неправильный ответ.
Реклама

1
Если вам дан четырехугольник произвольной формы, то даже для таких четырехугольников существуют формулы для вычисления их площадей. Обратите внимание, что такие формулы требуют знания тригонометрии.
- Во-первых, найдите длины всех четырех сторон. Обозначим их через a, b, c, d (а напротив с, а b напротив d).
- Пример: дан четырехугольник произвольной формы со сторонами 12 см, 9 см, 5 см и 14 см.
2
Найдите угол А между сторонами а и d и угол С между сторонами b и с (вы можете найти любые два противолежащих угла).
- Пример: в нашем четырехугольнике А = 80 градусов и C = 110 градусов.
3
Представьте, что существует отрезок, соединяющий вершины, образованные сторонами а и b и сторонами с и d. Этот отрезок разделит четырехугольник на два треугольника. Так как площадь треугольника равна 1/2absinC, где C — угол между сторонами a и b, вы можете найти площади двух треугольников и сложить их, чтобы вычислить площадь квадрата.
- Площадь = 0,5 х сторона1 х сторона4 х sin(угол между стороной1 и стороной4) + 0,5 х сторона2 х сторона3 х sin(угол между стороной2 и стороной3), или
- Площадь = 0,5 a × d × sin A + 0,5 × b × c × sin C
- Пример: вы нашли стороны и углы, поэтому просто подставьте их в формулу.
  
  = 0,5 (12 × 14) × sin (80) + 0,5 × (9 × 5) × sin (110)
  
  = 84 × sin (80) + 22,5 × sin (110)
  
  = 84 × 0,984 + 22,5 × 0,939
  
  = 82,66 + 21,13 = 103,79 квадратных сантиметров.
- Обратите внимание, что если вы пытаетесь найти площадь параллелограмма (у которого противоположные углы равны), то формула примет вид: площадь = 0.5*(ad + bc) * sin A
Реклама

Советы

Этот калькулятор для вычисления площади треугольника пригодится вам при вычислении площади четырехугольника произвольной формы.^[5]
Чтобы получить дополнительную информацию, прочитайте статьи по вычислению площади квадрата, площади прямоугольника, площади ромба, площади трапеции и площади дельтоида.

Об этой статье

Эту страницу просматривали 441 078 раз.

Была ли эта статья полезной?

Источник

решение:

Чтобы найти площадь данного четырехугольника, можем найти сначала площадь квадрата и четырех прямоугольных треугольников.

1)если посмотреть на рисунок видно, что квадрат со сторонами 5 и 5 см, находим его площадь:

S = a^2

S = 5^2

S = 25 (см^2)

2) смотрим на рисунок и видим, что у нас есть треугольники с катетами равными:

2 и 3 (см)
2 и 2 (см)
3 и 3 (см)
2 и 3 (см)

Найдем их площади:

S1 = 1/2 * 2 * 3 = 3 (см^2)

S2 = 1/2 * 2 * 2 = 2 (см^2)

S3 = 1/2 * 3 * 3 = 4,5 (см^2)

S4 = S1 = 3 (см^2)

3)чтобы найти площадь заданного четырехугольника, надо из площади квадрата отнять площади четырех прямоугольных треугольников:

S = 25 — (3 + 2 + 4,5 + 3)

S = 25 — 12,5

S = 12,5 (см^2)

Ответ: площадь заданного четырехугольника равна 12,5 см^2

Источник

Образцы вариантов ВПР 2023 года, демоверсии всероссийской проверочной работы для 4 класса по Математике.

Приобрести задания и ответы ВПР по Математике 4 класс

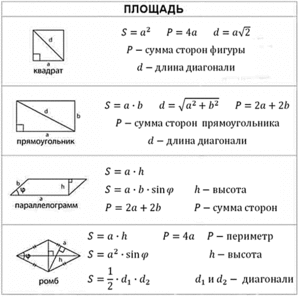
1. На клетчатом поле со стороной клетки 1 см изображён прямоугольник.

Найди площадь этого прямоугольника. Ответ дайте в квадратных сантиметрах.

2. Ниже на клетчатом поле со стороной клетки 1 см изображён прямоугольник.

Найди площадь этого прямоугольника. Ответ дайте в квадратных сантиметрах.

3. На клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди периметр этого прямоугольника. Ответ дайте в сантиметрах.

4. Ниже на клетчатом поле со стороной клетки 1 см изображён прямоугольник. Ответ укажите в см².

Найди площадь этого прямоугольника.

5. На клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди периметр этого прямоугольника. В ответе укажите число.

6. Ниже на клетчатом поле со стороной клетки 1 см изображён прямоугольник.

Найди площадь этого прямоугольника. В ответ впишите только число.

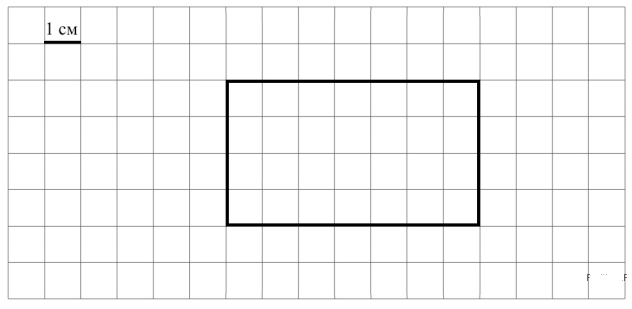
7. На клетчатом поле со стороной клетки 1 см изображён прямоугольник.

Найди периметр этого прямоугольника.

8. На рисунке изображена фигура.

Найди её площадь, если сторона одной клетки равна 1 см.

9. На рисунке изображена фигура.

Найди её площадь, если сторона одной клетки равна 1 см.

10. На рисунке изображена фигура.

Найди её площадь, если сторона одной клетки равна 1 см.

11. На рисунке изображена фигура.

Найди её площадь, если сторона одной клетки равна 1 см.

12. На рисунке изображён прямоугольник.

Найди его периметр, если сторона одной клетки равна 1 см.

13. На рисунке изображён прямоугольник.

Найди его периметр, если сторона одной клетки равна 1 см.

14. На рисунке изображён прямоугольник. Найди его периметр, если сторона одной клетки равна 1 см. Ответ запишите в сантиметрах.

15. На рисунке изображён прямоугольник.

Найди его периметр, если сторона одной клетки равна 1 см.

16. На рисунке изображён четырёхугольник.

Найди площадь данного на рисунке четырёхугольника.

17. На клетчатом поле со стороной клетки 1 см изображена геометрическая фигура. Найди периметр этой фигуры.

18. На рисунке изображён прямоугольник.

Найди его площадь.

19. На рисунке ниже изображена фигура.

Найди площадь этой фигуры, если сторона клетки  — 1 см.

20. На рисунке ниже изображена фигура.

Найди площадь этой фигуры, если сторона клетки  — 1 см.

21. На рисунке ниже изображена фигура.

Найди площадь этой фигуры, если сторона клетки  — 1 см. В ответе запишите только число.

22. Найди периметр этого прямоугольника, если сторона клетки  — 1 см. В ответе укажите число.

23. Найди периметр этого прямоугольника, если сторона клетки  — 1 см.

24. Найди периметр этого прямоугольника, если сторона клетки  — 1 см.
В ответе укажите число.

25. На рисунке ниже изображена фигура. Найди периметр этой фигуры. В ответе укажите число.

26. На рисунке ниже изображена фигура.

Найди периметр этой фигуры. Ответ дайте в метрах

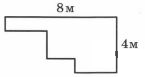
27. На рисунке изображён прямоугольник.

Найди площадь прямоугольника, если сторона клетки равна 1 см.

28. На рисунке изображён план игровой площадки.

Найди площадь игровой площадки, если длина одной клетки соответствует 1 м.

29. На рисунке изображён план коридора.

Найди площадь коридора, если длина одной клетки соответствует 1 м.

30. На рисунке внизу представлен эскиз крышки журнального столика. Найди площадь крышки столика, если длина одной клетки соответствует 1 дм. В ответе укажите число.

31. На изготовление витража понадобилось стекло прямоугольной формы.

Найди площадь этого стекла, если длина одной клетки соответствует 1 дм.

32. Для окна беседки в детском саду приготовили оргстекло прямоугольной формы. Найди площадь этого стекла, если длина одной клетки соответствует 1 дм.

Ответ запишите в квадратных дециметрах.

33. На рисунке дан чертёж кафельной плитки.

Найди площадь такой плитки, если сторона клетки  — 1 см.

34. На клетчатом поле со стороной клетки 1 см изображён прямоугольник. Ответ дайте в кв. см.

Найди площадь этого прямоугольника.

В ответе писать единицы измерения не нужно.

35. На клеточном поле со стороной клетки 1 см изображён квадрат.

Найди периметр этого квадрата.

В ответе писать единицы измерения не нужно.

36. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди площадь этой фигуры. Ответ дай в кв. см.

В ответе писать единицы измерения не нужно.

37. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди площадь этой фигуры. Ответ дай в кв. см.

В ответе писать единицы измерения не нужно.

38. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди площадь этой фигуры. Ответ дай в кв. см.

В ответе писать единицы измерения не нужно.

39. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди площадь этой фигуры. Ответ дай в кв. см.

40. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди площадь этой фигуры. Ответ дай в кв. см.

41. На клетчатой бумаге нарисован квадрат, а ниже  — некоторая фигура. Площадь квадрата равна 32 кв. см.

Найди площадь этой фигуры. Ответ дай в кв. см.

42. На клетчатой бумаге нарисован квадрат, а ниже  — некоторая фигура. Площадь квадрата равна 72 кв. см.

Найди площадь этой фигуры. Ответ дай в кв. см.

43. На клетчатой бумаге нарисован квадрат, а ниже  — некоторая фигура. Площадь квадрата равна 27 кв. см.

Найди площадь этой фигуры. Ответ дай в кв. см.

44. На клетчатой бумаге нарисован квадрат, а ниже  — некоторая фигура. Площадь квадрата равна 48 кв. см.

Найди площадь этой фигуры. Ответ дай в кв. см.

45. На клетчатой бумаге нарисован квадрат, а ниже  — некоторая фигура. Площадь квадрата равна 32 кв. см.

Найди площадь этой фигуры. Ответ дай в кв. см.

46. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди периметр этой фигуры. Ответ дай в сантиметрах.

47. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди периметр этой фигуры. Ответ дай в сантиметрах.

48. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди периметр этой фигуры. Ответ дай в сантиметрах.

49. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди периметр этой фигуры. Ответ дай в сантиметрах.

50. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди периметр этой фигуры. Ответ дай в сантиметрах.

51. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди площадь этой фигуры. Ответ дай в кв. см.

В ответе писать единицы измерения не нужно.

52. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди площадь этой фигуры. Ответ дай в кв. см.

В ответе писать единицы измерения не нужно.

53. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди площадь этой фигуры. Ответ дай в кв. см.

В ответе писать единицы измерения не нужно.

54. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди площадь этой фигуры. Ответ дай в кв. см.

В ответе писать единицы измерения не нужно.

55. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди площадь этой фигуры. Ответ дай в кв. см.

В ответе писать единицы измерения не нужно.

56. На клетчатом поле со стороной квадратной клетки 1 см изображена фигура.

Найди площадь этой фигуры. Ответ дай в квадратных сантиметрах.

В ответе писать единицы измерения не нужно.

57. На клеточном поле со стороной клетки 1 см изображён прямоугольник. Найди периметр этого прямоугольника. В ответе укажите число.

58. На клетчатом поле со стороной квадратной клетки 1 см изображена фигура.

Найди периметр этой фигуры.

59. На клеточном поле со стороной клетки 1 см изображён прямоугольник.

Найди площадь этого прямоугольника.

60. Ниже на клетчатом поле со стороной клетки 1 см изображён прямоугольник.

Найди площадь этого прямоугольника.

61. На клеточном поле со стороной клетки 1 см изображён прямоугольник.

Найди площадь этого прямоугольника.

62. На клеточном поле со стороной клетки 1 см изображён прямоугольник.

Найди площадь этого прямоугольника.

63. Ниже на клетчатом поле со стороной клетки 1 см изображён прямоугольник.

Найди площадь этого прямоугольника.

64. На клеточном поле со стороной клетки 1 см изображён прямоугольник.

Найди площадь этого прямоугольника.

65. На клетчатом поле со стороной клетки 1 см изображён прямоугольник.

Найди периметр этого прямоугольника.

66. На клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди периметр этого прямоугольника.

67. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см. Найди площадь этой фигуры. Ответ дай в квадратных сантиметрах.

68. Тип 5.1 № 2688

На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди площадь этой фигуры. Ответ дай в квадратных сантиметрах

69. Ниже на клетчатом поле со стороной клетки 1 см изображён прямоугольник.

Найди площадь этого прямоугольника.

70. Ниже на клетчатом поле со стороной клетки 1 см изображена фигура.

Найди площадь этой фигуры.

71. Ниже на клетчатом поле со стороной клетки 1 см изображена фигура.

Найди площадь этой фигуры.

72. На клетчатом поле со стороной клетки 1 см изображена фигура. Найди периметр этой фигуры.

73. На клетчатом поле со стороной клетки 1 см изображена фигура. Найди периметр этой фигуры.

74. На клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди площадь этого прямоугольника.

75. На клетчатом поле со стороной клетки 1 см изображена фигура. Найди периметр этой фигуры.

76. На клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди периметр этого прямоугольника.

77. На клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди площадь этого прямоугольника.

78. Ниже на клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди площадь этого прямоугольника.

79. Ниже на клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди площадь этого прямоугольника.

80. Ниже на клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди периметр этого прямоугольника. Ответ дайте в сантиметрах.

81. Ниже на клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди периметр этого прямоугольника.

82. На клетчатом поле со стороной квадратной клетки 1 см изображена фигура. Найди периметр этой фигуры.

83. Ниже на клетчатом поле со стороной клетки 1 см изображён прямоугольник.

Найди площадь этого прямоугольника.

84. Ниже на клетчатом поле со стороной клетки 1 см изображена фигура.

Найди периметр этой фигуры.

85. Ниже на клетчатом поле со стороной клетки 1 см изображена фигура.

Найди периметр этой фигуры.

86. Ниже на клетчатом поле со стороной клетки 1 см изображена фигура.

Найди периметр этой фигуры.

87. На клеточном поле со стороной клетки 1 см изображён квадрат.

Найди площадь этого квадрата. Ответ дайте в см².

88. На клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди периметр этого прямоугольника.

89. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди площадь этой фигуры. Ответ дай в кв. см.

В ответе писать единицы измерения не нужно.

90. На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

На клетчатой бумаге нарисована фигура. Сторона клетки равна 1 см.

Найди площадь этой фигуры. Ответ дай в кв. см.

В ответе писать единицы измерения не нужно.

91. На клетчатом поле со стороной квадратной клетки 1 см изображена фигура. Найди периметр этой фигуры.

92. На клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди периметр этого прямоугольника.

93. На клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди периметр этого прямоугольника.

94. На клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди периметр этого прямоугольника.

95. Ниже на клетчатом поле со стороной клетки 1 см изображена фигура. Найди периметр этой фигуры.

96. На клеточном поле со стороной клетки 1 см изображён прямоугольник. Найди площадь этого прямоугольника.

Источник