Как найти площадь четырехугольной наклонной призмы - Исправление недочетов и поиск решений вместе с Examum.ru

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.

Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.

Формула площади правильной призмы
- 1. Общая формула
- 2. Площадь правильной треугольной призмы
- 3. Площадь правильной четырехугольной призмы
- 4. Площадь правильной шестиугольной призмы
Примеры задач

Формула площади правильной призмы

1. Общая формула

Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.

S_полн. = S_бок. + 2S_осн.

Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.

S_бок. = P_осн. ⋅ h

Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.

2. Площадь правильной треугольной призмы

Основание: равносторонний треугольник.


Площадь	Формула
основание
боковая поверхность	S_бок. = 3ah
полная

microexcel.ru

3. Площадь правильной четырехугольной призмы

Основание: квадрат.


Площадь	Формула
основание	S_осн. = a²
боковая поверхность	S_бок. = 4ah
полная	S_полн. = 2a² + 4ah

microexcel.ru

Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a². А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a².

4. Площадь правильной шестиугольной призмы

Основание: правильный шестиугольник


Площадь	Формула
основание
боковая поверхность	S_бок. = 6ah
полная

microexcel.ru

Примеры задач

Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.

Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:

Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см². Найдите ее высоту, если известно, что сторона основания равна 5 см.

Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:

Источник

Многогранник, две грани которого равные -угольники, лежащие в параллельных плоскостях, а остальные граней – параллелограммы, называют -угольной призмой.

Два -угольника называют основаниями призмы, а параллелограммы – боковыми гранями. Стороны граней называют ребрами призмы, а концы ребер – вершинами призмы.

На рисунке 9.41 изображена пятиугольная призма, на рисунке 9.42 – треугольная, а на рисунке 9.43 – четырехугольная.

На рисунке 9.42 треугольники и – основания призмы , параллелограммы , , – боковые грани, отрезки , , – боковые ребра, отрезки , , , , , – ребра оснований, точки , , , , , – вершины призмы.

Если грани призмы не имеют общего ребра, то их называют противоположными, если грани имеют общее ребро, то – смежными. На рисунке 9.43 грани и , и , а также и являются противоположными, а, например, грани и – смежными.

Две вершины призмы, не принадлежащие одной грани, называют противоположными. Например, на рисунке 9.43 вершины и – противоположные.

Диагональю призмы называют отрезок, соединяющий две противоположные вершины (например, диагональ на рисунке 9.41).

Треугольная призма не имеет противоположных граней, не имеет противоположных вершин и не имеет диагоналей.

Прямой призмой называют призму, боковые ребра которой перпендикулярны плоскостям ее оснований (рис. 9.42). Боковые грани прямой призмы – прямоугольники.

Наклонной призмой называют призму, боковые ребра которой являются наклонными к плоскостям ее оснований (рис. 9.41 и 9.43). Боковые грани наклонной призмы – параллелограммы (некоторые боковые грани могут быть и прямоугольниками).

Высотой призмы называют перпендикуляр, заключенный между основаниями призмы. Высота прямой призмы равна длине ее бокового ребра (рис. 9.42), высота наклонной призмы – не равна (рис. 9.41 и 9.43).

Диагональным сечением призмы называют сечение, содержащее диагональ призмы. На рисунке 9.44 построены диагональные сечения и четырехугольной призмы .

Параллелепипедом называют призму, основание которой – параллелограмм (рис. 9.44).

Прямым параллелепипедом называют параллелепипед, боковые ребра которого перпендикулярны плоскостям его оснований (рис. 9.45).

Прямоугольным параллелепипедом называют прямой параллелепипед, основанием которого является прямоугольник. На рисунке 9.46 изображен прямоугольный параллелепипед.

Свойство диагонали прямоугольного параллелепипеда: квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений:

, (9.1)

где , , – длины ребер, выходящих из одной вершины, – диагональ параллелепипеда.

Объем прямоугольного параллелепипеда находят по формуле:

. (9.2)

Кубом называют прямоугольный параллелепипед с равными ребрами. Все грани куба – квадраты (рис. 9.47).

Объем куба с ребром находят по формуле:

. (9.3)

Площадь поверхности куба с ребром находят по формуле:

$LaTeX formula: S_{n.}=6a^2$ . (9.4)

Диагональ куба с ребром а находят по формуле:

. (9.5)

Объем прямой призмы высоты и периметром основания находят по формуле:

$LaTeX formula: V=S_{o.} cdot h$ . (9.6)

Площадь поверхности прямой призмы находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.7)

Площадь боковой поверхности прямой призмы высоты и периметром основания находят по формуле:

$LaTeX formula: S_{delta .}=P_{o.} cdot h$ . (9.8)

Объем наклонной призмы можно вычислить по формуле:

$LaTeX formula: V=S_{o.} cdot h$ . (9.9)

Площадь поверхности наклонной призмы можно вычислить по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ , (9.10)

а также по формулам:

$LaTeX formula: V=S_{c.} cdot l$ , (9.9.1)

$LaTeX formula: S_{delta.}=P_{c.} cdot l$ , (9.10.1)

где сечение, перпендикулярное ребру (рис. 9.48).

Правильной призмой называют прямую призму, основанием которой является правильный многоугольник.

Пример 1. Найдите объем и площадь поверхности куба, зная, что его диагональ см.

Решение. Согласно формуле 9.5 и см. По формуле 9.3 $LaTeX formula: V=(2sqrt{3})^2=24sqrt{3}$ ( $LaTeX formula: _{CM}\^3$ ), а по формуле 9.4 $LaTeX formula: S_{n.}=6 cdot (2sqrt{3})^2=72$ ( $LaTeX formula: _{CM}\^2$ ).

Ответ: $LaTeX formula: _{CM}\^3$ ; $LaTeX formula: _{CM}\^2$ .

Пример 2. Найдите объем прямоугольного параллелепипеда, диагональ которого равна , а его измерения относятся как .

Решение. Согласно условию задачи запишем измерения параллелепипеда: , , .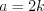

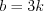
Согласно свойству диагонали прямоугольного параллелепипеда 9.1, получим: , , откуда . Тогда , , .

Зная три измерения параллелепипеда, по формуле 9.2 найдем его объем: .

Ответ: .

Пример 3. В основании прямой призмы лежит прямоугольный треугольник с катетами см и см. Высота призмы равна см. Найдите площадь поверхности и объем призмы.

Решение. 1. Площадь треугольника с катетами и найдем по формуле $LaTeX formula: S=frac{1}{2}ab$ . Получим: $LaTeX formula: S=frac{1}{2} cdot 10 cdot 8=40$ ( $LaTeX formula: _{CM}\^2$ ).

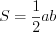
2. Гипотенузу найдем по теореме Пифагора: (см).

3. Площадь боковой поверхности призмы найдем по формуле 9.8 : $LaTeX formula: S_{delta .}=(10+8+2sqrt{41}) cdot 8=16(9+sqrt{41})$ ( $LaTeX formula: _{CM}\^2$ ).

4. Согласно формуле 9.7 , найдем площадь полной поверхности призмы:

$LaTeX formula: S_{n.}=2 cdot 40+16(9+sqrt{41})=16(14+sqrt{41})$ ( $LaTeX formula: _{CM}\^2$ ).

5. Объем призмы найдем по формуле 9.6 :

( $LaTeX formula: _{CM}\^3$ ).

Ответ: $LaTeX formula: _{CM}\^2$ ; $LaTeX formula: _{CM}\^3$ .

Пример 4. Объем наклонной треугольной призмы равен , а боковое ребро . Правильный треугольник – сечение, перпендикулярное боковому ребру (рис. 9.49). Найдите площадь боковой поверхности этой призмы.

Решение. 1. Согласно формуле 9.9.1 запишем: $LaTeX formula: 270=S_{c.} cdot 10$ , откуда $LaTeX formula: S_{c.}=27$ .

2. Площадь правильного треугольника со стороной находят по формуле $LaTeX formula: S=frac{sqrt{3}a^2}{4}$ . Тогда $LaTeX formula: 27=frac{sqrt{3}a^2}{4}$ , $LaTeX formula: a^2=9cdot 4cdot sqrt{3}$ , .

3. Найдем периметр треугольника : .

4. Согласно формуле 9.10.1 , найдем площадь боковой поверхности призмы: $LaTeX formula: S_{delta.}=18sqrt[4]{3} cdot 10=180sqrt[4]{3}$ .

Ответ: .

Пример 5. Диагональ прямоугольного параллелепипеда равна см, а диагонали его боковых граней равны см и см. Определите объем параллелепипеда.

Решение. Рассмотрим прямоугольный параллелепипед (рис. 9.50), где , и его измерения; см – диагональ.

Согласно свойству 9.1 . Рассмотрим треугольник . Так как см, то . Рассмотрим треугольник . Так как см, то .

Запишем и решим систему уравнений $LaTeX formula: begin{cases} a^2+b^2+c^2=36, \ b^2+c^2=16, \ a^2+c^2=25 . end{cases}$

Из второго уравнения системы выразим и получим: . Из третьего уравнения выразим и получим: .

Подставим полученные значения и в первое уравнение системы и найдем значение :

, , см.

Зная , определим значения и :

, см; , см.

Согласно формуле 9.2 найдем объем параллелепипеда: ( $LaTeX formula: _{CM}\^3$ ).

Ответ: $LaTeX formula: _{CM}\^3$ .

Пример 6. Определите объем правильной четырехугольной призмы, если ее диагональ образует с плоскостью боковой грани угол $LaTeX formula: 30^{circ}$ , а сторона основания равна .

Решение. Согласно условию задачи основанием призмы является квадрат со стороной (рис. 9.51).

Так как отрезок является проекцией диагонали призмы на грань , то угол является углом наклона диагонали призмы к плоскости боковой грани и $LaTeX formula: angle AB_1D=30^{circ}$ .

Рассмотрим треугольник . По свойству катета лежащего против угла $LaTeX formula: 30^{circ}$ запишем .

Так как согласно свойству 9.1 диагонали прямоугольного параллелепипеда , то , , .

Найдем объем призмы по формуле 9.9 :

Ответ: .

Пример 7. Найдите объем правильной шестиугольной призмы (рис. 9.52), зная, что большая диагональ призмы равна и образует с плоскостью основания призмы угол $LaTeX formula: 30^{circ}$ .

Решение. Рассмотрим большее диагональное сечение призмы и прямоугольный треугольник . Поскольку диагональ призмы и образует с плоскостью основания угол $LaTeX formula: 30^{circ}$ , то катет , лежащий против угла $LaTeX formula: 30^{circ}$ , равен половине гипотенузы, следовательно, высота призмы .

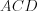
Из теоремы Пифагора: , , .

Так как в основании призмы лежит правильный шестиугольник со стороной , то и $LaTeX formula: a=frac{sqrt{3}}{2}$ .

По формуле $LaTeX formula: S=frac{3sqrt{3}a^2}{2}$ найдем площадь основания призмы: $LaTeX formula: S_{o.}=frac{9sqrt{3}}{8}$ .

По формуле 9.9 найдем объем призмы: $LaTeX formula: V=frac{9sqrt{3}}{8}$ .

Ответ: $LaTeX formula: frac{9sqrt{3}}{8}$ .

1. Треугольная призма не имеет диагоналей.

2. Различайте прямую и наклонную призму: у наклонной призмы – боковые грани параллелограммы, у прямой призмы – боковые грани прямоугольники.

3. Если основание призмы – параллелограмм (ромб, прямоугольник, квадрат), то такую призму называют параллелепипедом. Длины ребер, выходящих из одной вершины параллелепипеда, называют его измерениями.

Источник

Онлайн калькулятор площади боковой поверхности призмы быстро и точно вычислит площадь призмы по различным формулам. Расчет возможен для треугольной призмы, четырехугольной призмы и шестиугольной призмы.
Сделав расчет площади призмы на этом калькуляторы Вы не только получите ответ но еще и детальное пошаговое решение с выводом формул в общем виде.

Правильная призма — это прямая призма, основанием которой является правильный многоугольник, а боковые грани перпендикулярны основаниям.

Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.

Источник

ВИДЕОУРОК

Призма называется наклонной, если её боковые рёбра не
перпендикулярны к плоскости основания.

Если в наклонной призме боковое ребро образует одинаковые
углы со сторонами основания, которые выходят из его одного конца, то проекция
ребра на плоскость основания будет биссектрисою соответственного угла основания.

Если в наклонной призме две смежные боковые грани образуют
одинаковые двугранные углы с основанием, то проекция на основание бокового
ребра, которое принадлежит линии пересечения двух граней указанных двугранных углов,
будет биссектрисою угла основания.

Поверхность наклонной призмы.

Боковою поверхностью наклонной призмы называется сумма
площадей всех её боковых граней.

Полною поверхностью наклонной призмы называется сумма её боковой
поверхности и площадей оснований.

S_п = S_б + 2S_осн.

Боковая поверхность наклонной призмы равна произведению
периметра перпендикулярного сечения на боковое ребро.

S_б = P_пер × AA₁,

где P_пер – периметр сечения, перпендикулярного к боковому
ребру.

ЗАДАЧА:

В наклонной призме проведено сечение,
перпендикулярное боковым рёбрам и пересекающее все боковые рёбра. Найдите площадь
боковой поверхности призмы, если периметр сечения равен р,
а боковое ребра равно l.

РЕШЕНИЕ:

Пусть в наклонной призме
проведено сечение, перпендикулярное боковым рёбрам, и пересекающее все боковые
рёбра (сечение KLM). Плоскость
проведенного сечения разбивает призму на две части.

Применим к одной из них параллельное
перемещение, которое совмещает основания призмы. При этом получим прямую
призму, основанием которой будет сечение данной призмы, а боковые ребра равны l. Эта
призма имеет туже самую боковую поверхность, что и данная. Таким образом, площадь
боковой поверхности данной призмы равна рl.

ЗАДАЧА:

В наклонной треугольной призме боковые
рёбра равны 8
см; стороны перпендикулярного сечения относятся как

9 : 10 : 17,

а его площадь равна 144
см². Найдите
боковую поверхность этой призмы.

РЕШЕНИЕ:

Пусть дана призма АС₁;

АА₁ = ВВ₁ =
СС₁ =
8 см,

А₂В₂С₂ – перпендикулярное сечение призмы, притом

А₂В₂ : В₂С₂ : С₂ А₂ = 9 : 10 : 17 і

Необходимо определить боковую
поверхность призмы:

S_бок = (А₂В₂ + В₂С₂ + С₂ А₂) × АА₁.

По условию задачи

АА₁ =
8 см, а

А₂В₂ : В₂С₂ : С₂ А₂ = 9 : 10 : 17.

Обозначим:

А₂В₂ = 9х, В₂С₂ = 10х, С₂А₂ = 17х.

Тогда по формуле Герона площадь
перпендикулярного сечения будет равно:

а по условию она равна 144
см²,
то есть

36х² =
144, откуда х = 2 см.

В таком случае

А₂В₂ + В₂С₂ + С₂ А₂

= 36х = 72 см,

то есть

S_бок = 72 × 8 см² = 576 см².

ОТВЕТ: 576 см²

Задания к уроку 3

Задание 1
Задание 2
Задание 3

Другие уроки:

Урок 1. Прямые и плоскости в пространстве
Урок 2. Прямая призма
Урок 4. Правильная призма
Урок 5. Параллелепипед
Урок 6. Прямругольный параллелепипед
Урок 7. Куб
Урок 8. Пирамида
Урок 9. Правильная пирамида
Урок 10. Усечённая пирамида
Урок 11. Цилиндр
Урок 12. Вписанная и описанная призмы
Урок 13. Конус
Урок 14. Усечённый конус
Урок 15. Вписанная и описанная пирамиды
Урок 16. Сфера и шар
Урок 17. Комбинация тел

Источник

Вы здесь:

Главная
Правильная четырехугольная призма

Правильная четырехугольная призма

Четырехугольная призма — это многогранник, две грани которого являются равными квадратами, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими квадратами.

Правильная четырехугольная призма — это четырехугольная призма у которой основания квадраты, а боковые грани прямоугольники.

Данное геометрическое тело по своим свойствам и характеристикам соответствует — параллелепипеду.

Основания призмы являются равными квадратами.

Боковые грани призмы являются прямоугольниками.

Боковые рёбра призмы параллельны и равны.

Размеры призмы можно выразить через длину стороны a и высоту h.

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

Формула площади поверхности четырехугольной призмы:

Объём призмы равен произведению её высоты на площадь основания.

Формула объема правильной четырехугольной призмы:

Правильная четырехугольная призма может быть вписана в цилиндр.

Формула радиуса цилиндра вписанной четырехугольной призмы:

Двойственным многогранником прямой призмы является бипирамида.

Исторически понятие «призма» возникло из латыни и означало — нечто отпиленное.

Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.