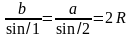Оглавление
Введение…………………………………………………………………………………….3
Глава
I.
Дельтоид — один из видов четырехугольников………………………………..4
1.1.
Определение дельтоида……………………………………………..……………4
1.2.
Признаки дельтоида………………………………………………………………5
1.3.
Свойства дельтоида……………………………………………………………….6
1.4.
Формулы для нахождения площади дельтоида………………………………….6
Глава II.
Задачи по теме «Дельтоид»………………………………………………….…8
Заключение……………………………………………………………………………….10
Библиографический список……………………………………………………………..11
Приложения………………………………………………………………………………12
Введение
В прошлом учебном году на уроках
геометрии нами изучалась тема «Четырехугольники». Мы узнали свойства
прямоугольника, параллелограмма, трапеции, ромба, квадрата. Возник вопрос: все
ли виды четырехугольников нам теперь известны. Работая с дополнительной
литературой, мы узнали о дельтоиде и решили подробнее рассмотреть эту
геометрическую фигуру.
Цель: изучить геометрическую
фигуру дельтоид.
Задачи:
— познакомиться с литературой
по данной теме;
—
сформулировать определения дельтоида, сравнить их;
—
найти и доказать свойства и признаки дельтоида;
—
рассмотреть формулы для нахождения площади дельтоида;
—
рассмотреть задачи, в которых используется фигура дельтоид.
Объект исследования: фигура
дельтоид.
Предмет исследования: определение,
свойства и признаки дельтоида, способы вычисления площади дельтоида.
Методы исследования: работа
с научной литературой, анализ и систематизация теоретического материала, доказательство
теорем, решение задач.
Глава
I.
Дельтоид – один из видов четырёхугольников.
1.1.
Определение дельтоида.
Анализируя
учебники геометрии и справочники по математике для школьников, мы не нашли
определений дельтоида. Но изучив дополнительные источники и пособия, выделили
четыре определения.
1)
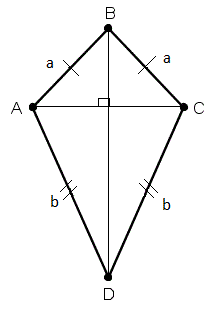
Дан четырёхугольник ABCD,
в котором AB=BC
и AD=DC.
Такой четырёхугольник называется дельтоидом [6, 4].
2)
Дельтоидом называется четырёхугольник,
который имеет две пары равных соседних сторон [8].
3)
Дельтоид — это выпуклый четырёхугольник,
состоящий из двух различных равнобедренных треугольников с общим основанием,
вершины которых лежат по разные стороны от этого основания [9].
4)
Четырёхугольник, симметричный относительно
одной из своих диагоналей, называется дельтоидом [2].
Учитывая,
что дельтоид может быть выпуклым или невыпуклым, утверждение 3 нельзя считать
определением дельтоида. Оно является определением выпуклого дельтоида.
Дельтоид
имеет две диагонали – главную и неглавную.
Главная
диагональ дельтоида – отрезок, который соединяет вершины двух неравных углов
дельтоида.
Неглавная
диагональ дельтоида – отрезок, который соединяет вершины двух равных углов
дельтоида.
Средняя линия дельтоида —
отрезок, соединяющий середы смежных сторон.
1.2.
Признаки дельтоида.
Первый признак
дельтоида: если в четырёхугольнике одна из двух
взаимно перпендикулярных диагоналей является биссектрисой, не равных
противоположных углов, а другая не является биссектрисой другой пары углов, то
такой четырёхугольник — дельтоид.
Доказательство:
|
Дано: Четырехугольник ABCD, AC (∠ AC Доказать: ABCD |
|
Доказательство:
1.
Точка O
– точка пересечения диагоналей АС и ВD,
AС
┴ BD.
Рассмотрим
∆ АОB
и ∆ АОD:
∆ AOB
и ∆ AOD
– прямоугольные треугольники, так как AC
┴ BD
по условию, АО – общая сторона, ∠ OAB
= ∠ OAD
по условию, тогда ∆ АОD = ∆ АОВ по катету
и прилежащему к нему острому углу, значит АB
= АD.
2. Точка O – точка пересечения
диагоналей, CO ┴ BD.
Рассмотрим
∆ СОB
и ∆ СОD:
∆ COB
и ∆ COD
– прямоугольные треугольники, так как AC
┴ BD
по условию, ОС — общая сторона, ∠ BCA
= ∠ DCA
по условию, тогда ∆ СОD = ∆ СОВ по
катету и прилежащему к нему острому углу, значит BС=DС.
3. Так как AB = AD,
BC
= DC,
то ABCD
– дельтоид по определению.
Второй
признак дельтоида: если в четырёхугольнике только одна
из диагоналей точкой пересечения с другой диагональю делится пополам и
перпендикулярна ей, то такой четырёхугольник дельтоид.
Доказательство:
|
Дано: Четырехугольник ABCD, Точка O BO Доказать: ABDC |
|
Доказательство:
1.
Рассмотрим ∆ АОB
и ∆ АОD:∆ AOB и ∆ AOD
– прямоугольные треугольники, так как AC
┴ BD
по условию, АО – общая сторона, BO
= OD
по условию, тогда ∆ АОD = ∆ АОВ по двум
катетам, значит АB = АD.
2.
Рассмотрим ∆ COB
и ∆ COD:∆
COB
и ∆ COD
– прямоугольные треугольники, так как AC
┴ BD
по условию, ОС – общая сторона, BO
= OD
по условию, тогда ∆ СОB = ∆ СОD
по двум катетам, значит BС = DC.
3.
Так как AB
= AD,
BC
= DC,
то ABCD
– дельтоид по определению.
1.3.
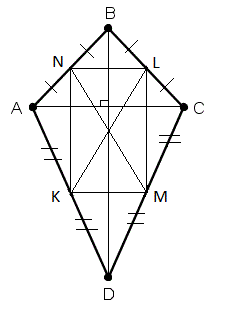
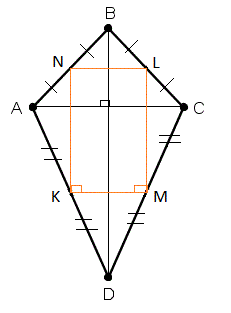
Свойства дельтоида (см. Приложение 1).
1.
Углы между сторонами разной длины равны.
2.
Неглавная диагональ делит дельтоид на два
равнобедренных треугольника.
3.
Главная диагональ делит дельтоид на два
равных треугольника.
4.
Главная диагональ является биссектрисой
углов.
5.
Точка пересечения диагоналей делит
неглавную диагональ на две равные части.
6.
Диагонали дельтоида (или их продолжения) взаимно
перпендикулярны.
7.
В дельтоид всегда можно вписать
окружность.
8.
Главная диагональ — ось симметрии.
9.
Для дельтоида параллелограммом Вариньона
является прямоугольник. (Параллелограмм Вариньона – четырехугольник, вершины
которого совпадают с серединами сторон произвольного четырёхугольника).
1.4.
Формулы для нахождения площади дельтоида.
Площадь дельтоида можно вычислить по
четырём формулам:
1) S
=
, где
— диагонали дельтоида
Доказательство:
2) S
= ab sin α , где a
и b
– неравные стороны, α – угол между ними
Доказательство:
3) S
=
sin
+
sin
, где a
и b
– неравные стороны, — угол между сторонами
равными a,
— угол между сторонами
равными b
Доказательство:
4) S
= (a+b)
r , где a
и b
– неравные стороны, r – радиус
вписанной окружности
Доказательство:
|
Докажем сначала, Если r – радиус вписанной в
|
|
Глава II.
Задачи по теме «Дельтоид».
Изучив
некоторые российские учебные пособия по математике, мы не встретили системы задач
про дельтоид. Есть задачи про равнобедренные треугольники с общим основанием, про
биссектрису угла, т.е. при решении образуется дельтоид, например №123, №142,
№172, №175, №247, учебника по геометрии 7-9 Л.С. Атанасяна. Тем не менее, мы обнаружили информацию и задачи в
иностранной учебной литературе (см. Приложение 2). Примеры некоторых
переведенных нами задач приведены ниже:
Задача
1.
|
Дано: ABCD AB = AD, FC = 8 см, Найти: |
|
Решение:
ABCD – дельтоид по
условию. Так как AC┴BD
по свойству дельтоида, то ∆ DEC
– прямоугольный треугольник, = CF∙CD
по теореме о пропорциональных отрезках в прямоугольном треугольнике, = 8 ∙ (8 + 2) = 80, EC
= 4 см.
= FD
∙ DC
по теореме о пропорциональных отрезках в прямоугольном треугольнике
= 2 ∙ (2 +

см,
=
,
=
= 50
Ответ: 50
Задача
2.
|
Дано: ∆ ABC, EC = 2AE, FE = DE, AF = 2 см, Найти: FB |
|
Решение:
Так как FE
= DE,
FB
= BD
по условию, то BDEF – дельтоид по
определению дельтоида
BE – биссектриса BDEF
по свойству дельтоида, AE = a
, EC
= 2a
, так как EC = 2AE
по условию
=
по свойству биссектрисы,
=
=
, 2х + 4 = х + 5, х = 1, FB
= BD
= 1 см
Ответ: 1 см
Задача
3.
|
Дано: ABCD AB = BC Найти: ED |
|
Решение:
1)
∆ ABC
– равнобедренный прямоугольный треугольник, AB
= BC
= 2 см по условию, значит
+
=
по теореме Пифагора, AC
= 4 см
2)
AC
┴ BD
по свойству дельтоида, значит, ∆ KCD
– прямоугольный треугольник,
AK = KC
= 2 см, так как BK – медиана
равнобедренного треугольника ABC
= CE
∙ CD
по теореме о пропорциональных отрезках в прямоугольном треугольнике
= 1 ∙ (1 + ED),
ED
= 3 см
Ответ: 3 см
Задача
4.
|
Дано: ABCD ∠ BAD = 100°, Найти: ∠ |
|
Решение:
∠ BAD
= ∠ BCD
= 100° по свойству дельтоида, ∠ BCE
= 100° — 80° = 20°
∠ BEC
= 90°, так как CE ┴ AB
по условию, ∠ EBC
+ ∠ BCE
+ ∠ BEC
= 180° по теореме о сумме углов треугольника, тогда ∠
EBC
= 180° — 20° — 90° = 70°.
BD – биссектриса ABCD
по свойству дельтоида, ∠ DBC
= ∠ ABD
= = 35° по определению
биссектрисы
Ответ: 35°
Заключение.
При
изучении темы «Четырёхугольники» дельтоид, как геометрическая фигура, не
рассматривается совершенно напрасно, т.к. эту фигуру мы часто встречаем в
окружающем мире. В своей исследовательской работе мы постарались восполнить
этот пробел школьной программы. Доказательства признаков и свойств дельтоида
доступны учащимся общеобразовательных школ, т.к. не являются особо сложными.
Содержание задач можно разнообразить, составив еще более сложные задачи, а так
же задачи на построение или комбинацию дельтоида с другими фигурами. Считаем,
что цели и задачи, поставленные нами в работе, достигнуты.
Библиографический список.
1.
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.
и др. Геометрия 7-9 классы: учеб. для общеобразоват.
организаций.-М.:Просвещение, 2013.-383с.
2.
Бутузов В.Ф., Дубровский В.Н., Кадомцев
С.Б. Геометрия. 9 класс [Электронный ресурс]: программный продукт
«1С»-учеб.электрон.изд.-ООО «1С-Паблишинг», 2009. — 1 электорн.опт.диск (CD—ROM)
3.
Киселев А.П. Геометрия / Под ред. Н.А.Глаголева.-М.:ФИЗМАТЛИТ,2013.-328с.
4.
Титаренко А.М., Роганин А.Н. Новейший
полный справочник школьника:5-11 классы.-М.:Эксмо, 2008.-304с.
5.
Цыпкин А.Г. Справочник по математике для
средней школы.-М.:Наука.Главная редакция физико-математической литературы,
1981.-400с.
6.
Шноль Д, Сгибнев А, Нетрусова Н. Система
открытых задач по геометрии: 8 класс – М.: Чистые пруды, 2009. – 32 с.: ил. –
(Библиотечка «Первого сентября», серия «Математика». Вып. 29).
7.
Энциклопедический словарь юного математика
/ Сост. А.П.Савин. -М.:Педагогика,1989.-352с.
8.
Математика для школы [Электронный
ресурс] -Режим доступа : http://math4school.ru/chetyrehugolniki.html
9.
Четырехугольники [Электронный ресурс]:
учебный центр «Резольвента» / Режим доступа: http://www.resolventa.ru/
10.
http://www.matematikkalesi.com/tr/
ПРИЛОЖЕНИЕ 1
Доказательства свойств дельтоида
1.
Углы между сторонами разной длины равны.
|
Дано: ABCD Доказать: ∠ BAD |
|
Доказательство:
1.
Рассмотрим ∆ ABC, AB
= BC
по определению дельтоида, тогда ∆ ABC
– равнобедренный, значит ∠ BAC
= ∠ BCA
2.
Рассмотрим ∆ ADC,
AD
= CD
по определению дельтоида, тогда ∆ ADC
– равнобедренный, значит ∠ DAC
= ∠ DCA
3.
Так как ∠ BAC
= ∠ BCA,
∠ DAC
= ∠ DCA,
то ∠ BAD
= ∠ BCD
2.
Неглавная диагональ делит дельтоид на два
равнобедренных треугольника.
|
Дано: ABCD Доказать: ∆ ABC ∆ ADC |
|
Доказательство
1.
Рассмотрим ∆ ABC, AB
= BC
по определению дельтоида, тогда ∆ ABC
– равнобедренный
2.
Рассмотрим ∆ ADC,
AD
= CD
по определению дельтоида, тогда ∆ ADC
– равнобедренный
3. Главная
диагональ делит дельтоид на два равных треугольника.
|
Дано: ABCD Доказать: ∆ ABD |
|
Доказательство:
AB
= BC
по определению дельтоида, AD
= CD
по определению дельтоида, BD
– общая сторона, тогда ∆ABD = ∆CBD
по третьему признаку равенства треугольников (по трём сторонам)
4. Главная
диагональ является биссектрисой углов.
|
Дано: ABCD Доказать: ∠ ABD |
|
Доказательство:
1.
AB
= BC
по определению дельтоида, AD
= CD
по определению дельтоида, BD
– общая сторона, тогда ∆ ABD = ∆ CBD
по третьему признаку равенства треугольников (по трём сторонам)
2.
Так как ∆ ABD
= ∆ CBD,
то ∠ ABD = ∠
CBD,
∠
ADB
= ∠ CDB
5.
Точка пересечения диагоналей делит
неглавную диагональ на две равные части.
|
Дано: ABCD Точка O Доказать: AO |
|
Доказательство:
1.
AB
= BC
по определению дельтоида, BO
– общая сторона, ∠ABO
= ∠CBO по свойству
дельтоида, тогда ∆ ABO = ∆ CBO
по первому признаку равенства треугольников (по двум сторонам и углу между
ними)
2.
Так как ∆ ABO
= ∆ CBO,
то AO
= OC
6.
Диагонали дельтоида (или их продолжения)
взаимно перпендикулярны.
|
Дано: ABCD Точка O Доказать: AC |
|
Доказательство:
1.
Рассмотрим ∆ ABC, AB
= BC
по определению дельтоида, тогда ∆ ABC
– равнобедренный
2.
BO
– биссектриса ∆ ABC, значит BO
– медиана и высота ∆ ABC
3.
Так как BO
— высота ∆ ABC, значит AC
┴ BD
ПРИЛОЖЕНИЕ 2
Муниципальное автономное общеобразовательное учреждение
«Средняя общеобразовательная школа № 7» города Когалыма
Исследовательская работа
Дельтоид
Автор: Полякова Анастасия ,
8 «И» МАОУ СОШ №7
Руководитель:
Ионга Ирина Николаевна,
учитель математики
г. Когалым, 2019
СОДЕРЖАНИЕ
1. Введение…………………………………………………………………………………3
2. Дельтоид…………………………………………………………………………………4
2.1 Определение дельтоида…………………………………………………………………………4
2.2 Признаки дельтоида………………………………………………………………..5
2.3 Свойства дельтоида…………………………………………………………………7
2.4 Формула площади дельтоида………………………………………………………7
3. Решение задач…………………………………………………………………………..8
4.Заключение……………………………………………………………………………..10
5. Список используемых источников…………………………………………..………10
ВВЕДЕНИЕ
В школе на уроках геометрии мы изучали различные четырехугольники. Узнав про дельтоид, я решила дополнительно изучить различные его свойства и признаки.
АКТУАЛЬНОСТЬ
Дельтоид – сложная, но интересная геометрическая фигура. Поискав информацию про дельтоид в различных школьных учебниках геометрии, я ничего не смогла найти. Именно поэтому будет очень интересно изучить эту геометрическую фигуру и научиться решать задачи, применяя ее свойства. Я считаю, что изучение дельтоида актуально для школьников, так как некоторые задачи в геометрии можно решить с помощбю его свойств.
Объект исследования: четырехугольник дельтоид
Цель: изучить дельтоид как геометрическую фигуру
Задачи:
— сформулировать определение дельтоида
— доказать признаки и рассмотреть свойства дельтоида
— рассмотреть формулу для нахождения площади дельтоида
— научиться решать задачи по теме «Дельтоид»
Объект исследования: дельтоид.
Предмет исследования: свойства и признаки дельтоида.
Метод исследования: изучение свойств, признаков дельтоида и задач про дельтоид.
ДЕЛЬТОИД
ОПРЕДЕЛЕНИЕ ДЕЛЬТОИДА
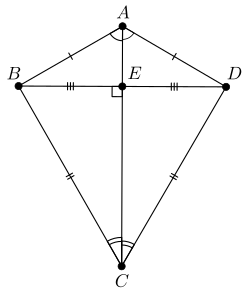
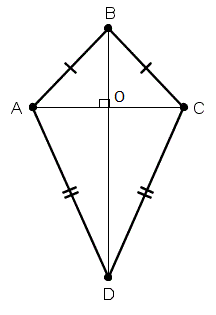
Дельтоид – это четырёхугольник, обладающий двумя парами сторон одинаковой длины, причем равными являются две пары смежных сторон.
Дельтоид бывает выпуклым и невыпуклым.
Дельтоид имеет две диагонали – главную и неглавную.
Дельтоид часто встречается в окружающем нас мире. Например, воздушный змей имеет форму дельтоида.
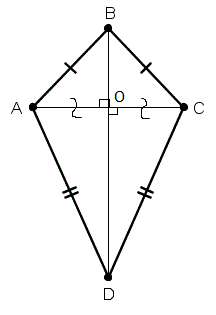
ПРИЗНАКИ ДЕЛЬТОИДА
Первый признак дельтоида: если в четырёхугольнике одна из двух взаимно перпендикулярных диагоналей является биссектрисой, не равных противоположных углов, а другая не является биссектрисой другой пары углов, то такой четырёхугольник – дельтоид.
Давайте докажем первый признак дельтоида.
Дано: ABCD – четырехугольник, AC ⊥ BD, AC – биссектриса, ∠BCO=∠OCD, ∠BAO=∠OAD
Доказать: ABCD – дельтоид
Решение.
Докажем, что BC=CD и BA=DA.
Рассмотрим △BCO и △DCO. Они равны по 2 признаку равенства треугольников (CO – общая, ∠BCO=∠OCD(по условию), ∠COD=∠COB(по условию)). Поэтому, BC=CD.
Рассмотрим △BAO и △DAO. Они равны по 2 признаку равенства треугольников (AO – общая, ∠BAO=∠DAO(по условию), ∠BOA=∠DOA(по условию)). Поэтому, BA=DA.
Из этого следует, что ABCD – дельтоид, чтд.
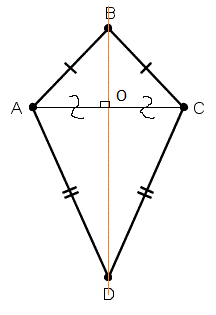
Второй признак дельтоида: если в четырёхугольнике только одна из диагоналей точкой пересечения с другой диагональю делится пополам и перпендикулярна ей, то такой четырёхугольник дельтоид.
Докажем второй признак дельтоида.
Дано: ABCD – четырехугольник, AC ⊥ BD, BO=OD
Доказать: ABCD – четырёхугольник
Решение.
Докажем, что BC=CD и BA=DA.
Рассмотрим △BCO и △DCO. Они равны по1 признаку равенства треугольников (CO – общая, BO=OD (по условию), ∠COD=∠COB(по условию)). Поэтому, BC=CD.
Рассмотрим △BAO и △DAO. Они равны по 1 признаку равенства треугольников (AO – общая, BO=∠OD(по условию), ∠BOA=∠DOA(по условию)). Поэтому, BA=DA.
Из этого следует, что ABCD – дельтоид, чтд.
СВОЙСТВА ДЕЛЬТОИДА
- Углы между сторонами неравной длины равны.
- Диагонали взаимно перпендикулярны.
- В любой выпуклый дельтоид можно вписать окружность; кроме того, если дельтоид не является ромбом, то существует ещё одна окружность, касающаяся продолжений всех четырёх сторон
- Для любого невыпуклого дельтоида можно построить окружность, касающуюся двух больших сторон и продолжений двух меньших сторон, и окружность, касающуюся двух меньших сторон и продолжений двух больших сторон.
- Точка пересечения диагоналей делит одну из них пополам.
- Другая диагональ является биссектрисой углов.
- Одна диагональ делит дельтоид на два равных треугольника.
- Другая диагональ делит дельтоид на два равнобедренных треугольника, если он выпуклый, и достраивает его равнобедренным треугольником до равнобедренного треугольника, если он невыпуклый.
ФОРМУЛА ПЛОЩАДИ ДЕЛЬТОИДА
Площадь дельтоида, можно найти по формуле: S = (a + b) r, где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности
РЕШЕНИЕ ЗАДАЧ
Я нашла в интернете несколько интересных задач про дельтоид. Давайте решим их.
Задача 1.
Дано: ABCD – дельтоид, AD=2AB, P=60см
Найти: AB, BC, CD, AD
Решение:
Так как ABCD – дельтоид, то AB=DC и AD=DC
Пусть AB – х, тогда AD – 2х
Составим уравнение:
х+х+2х+2х=60
6х=60
х=10
AB=BC=10
AD=CD=2AB=10*2=20
Ответ: 10,10,20,20
Задача 2.
Построить дельтоид по двум неравным сторонам и диагонали.
- Построим отрезок AC
- Построим серединный перпендикуляр к отрезку AC.
- Построим окружность с радиусом a и центром в точке A.
- Найдем точку B пересечения окружности и перпендикуляра с.
- Построим отрезки AB и BC.
- Построим окружность с радиусом b и центром в точке А.
- Найдем точку D пересечения окружности и перпендикуляра с.
- Построим отрезки AD и CD.
Задача 3.
Дано: ABCD – дельтоид, Р△ABD=15см, BD=6см, OC=4см
Найти: PABCD
Решение:
AD+AB= Р△ABD-BD=15-6=9см
DO=OB=6:2=3см
DC==
=
=5
PABCD=DA+AB+BC+DC
PABCD=9+5+5=19см
Ответ: 19 см
ЗАКЛЮЧЕНИЕ
Таким образом, было дано определение дельтоида, были рассмотрены его свойства и формула его площади. Были рассмотрены задачи на применение свойств дельтоида и задачи на нахождение его площади. Цель работы выполнена.
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
https://ru.wikipedia.org/wiki/%D0%94%D0%B5%D0%BB%D1%8C%D1%82%D0%BE%D0%B8%D0%B4
https://www.resolventa.ru/spr/planimetry/sqf.htm
Загрузить PDF
Загрузить PDF
Вам дана задача, в которой требуется найти площадь четырехугольника, а вы даже не знаете, что такое четырехугольник? Не волнуйтесь, эта статья вам поможет! Четырехугольник — это любая фигура с четырьмя сторонами. Для вычисления площади четырехугольника нужно определить тип четырехугольника, который вам дан, и воспользоваться соответствующей формулой.
-
1
Определение параллелограмма. Параллелограмм — это четырехугольник, у которого противоположные стороны равны и параллельны друг другу. Квадраты, прямоугольники и ромбы — это параллелограммы.
- Квадрат — это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
- Прямоугольник — это параллелограмм, у которого все стороны пересекаются под прямым углом.
- Ромб — это параллелограмм, у которого все стороны равны.
-
2
Площадь прямоугольника. Чтобы вычислить площадь прямоугольника, нужно знать его ширину (короткая сторона; представьте ее как высоту) и длину (длинная сторона; представьте ее как сторону, к которой проведена высота). Площадь прямоугольника равна произведению длины на ширину.
- ‘Площадь = длина х высота, или S = a х h.
- Пример: если длина прямоугольника равна 10 см, а ширина равна 5 см, то площадь этого прямоугольника: S = 10 х 5 = 50 квадратных сантиметров.
- Не забывайте, что площадь измеряется в квадратных единицах (квадратных метрах, квадратных сантиметрах и так далее).
-
3
Площадь квадрата. Квадрат — это частный случай прямоугольника, поэтому используйте ту же формулу, что и для нахождения площади прямоугольника. Но в квадрате все стороны равны, поэтому площадь квадрата равна любой из его сторон, возведенной в квадрат (то есть умноженной саму на себя).[1]
- Площадь = сторона х сторона, или S = a2.
- Пример: если сторона квадрата равна 4 см (a = 4), то площадь этого квадрата: S = a2 = 4 х 4 = 16 квадратных сантиметров.
-
4
Площадь ромба равна произведению его диагоналей, разделенной на два. Диагонали — это отрезки, соединяющие противоположные вершины ромба.[2]
- Площадь = (диагональ1 х диагональ2)/2, или S = (d1 × d2)/2
- Пример: если диагонали ромба равны 6 см и 8 см, то площадь этого ромба: S = (6 х 8)/2 = 24 квадратных сантиметров.
-
5
Площадь ромба также можно найти, если умножить его сторону на высоту, опущенную на эту сторону. Но не путайте высоту со смежной стороной. Высота — это прямая, опущенная из любой вершины ромба на противоположную сторону, и пересекающая противоположную сторону под прямым углом.
- Пример: если длина ромба равна 10 см, а его высота равна 3 см, то площадь такого ромба равна 10 х 3 = 30 квадратных сантиметров.
-
6
Формулы для вычисления площадей ромба и прямоугольника применимы к квадратам, так как квадрат — это частный случай как прямоугольника, так и ромба.
- Площадь = сторона х высоту, или S = a × h
- Площадь = (диагональ1 × диагональ2)/2, или S = (d1 × d2)/2
- Пример: если сторона квадрата равна 4 см, то его площадь равна 4 х 4 = 16 квадратных сантиметров.
- Пример: диагонали квадрата равны по 10 см. Вы можете найти площадь этого квадрата по формуле: (10 х 10)/2 = 100/2 = 50 квадратных сантиметров.
Реклама
-
1
Определение трапеции. Трапеция — это четырехугольник, у которого две противоположные стороны параллельны друг другу. Каждая из четырех сторон трапеции может быть разной длины.
- Есть два способа вычисления площади трапеции (в зависимости от данных значений).
-
2
Найдите высоту трапеции. Высота трапеции — отрезок, соединяющий параллельные стороны (основания) и пересекающий их под прямым углом (высота не равна боковым сторонам). Вот как найти высоту трапеции:[3]
- Из точки пересечения меньшего основания и боковой стороны проведите перпендикуляр к большему основанию. Этот перпендикуляр и есть высота трапеции.
- Чтобы вычислить высоту, используйте тригонометрию. Например, если вы знаете боковую сторону и прилегающий к ней угол, то высота равна произведению боковой стороны на синус прилегающего угла.
-
3
Найдите площадь трапеции, используя высоту. Если вы знаете высоту трапеции и оба основания, используйте следующую формулу для вычисления площади трапеции:
- Площадь = (основание1 + основание2)/2 × высота, или S = (a+b)/2 × h
- Пример: если высота трапеции равна 2 см, а основания трапеции равны 7 см и 11 см, то площадь этой трапеции: S = (a+b)/2 * h = (7 + 11)/2 * 2 = 18 квадратных сантиметров.
- Если высота трапеции равна 10, а основания трапеции равны 7 и 9, то площадь этой трапеции: S = (a+b)/2 * h = (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80.
-
4
Найдите площадь трапеции, используя среднюю линию. Средняя линия — это отрезок, параллельный основаниям и делящий боковые стороны пополам. Средняя линия равна среднему значению от обоих оснований (a и b): средняя линия = (a+b)/2.
- Площадь = средняя линия х высота, или S = m × h
- По сути, здесь вы используете формулу для нахождения площади трапеции по двум основаниям, но вместо (a+b)/2 подставлена m (средняя линия).
- Пример: если средняя линия трапеции равна 9 см, то площадь этой трапеции: S = m*h = 9 х 2 = 18 квадратных сантиметров (вы получили тот же ответ, что и в предыдущем шаге).
Реклама
-
1
Определение дельтоида. Дельтоид — это четырехугольник с двумя парами сторон одинаковой длины.
- Есть два способа вычисления площади дельтоида (в зависимости от данных значений).
-
2
Найдите площадь дельтоида, используя формулу для нахождения площади ромба (с использованием диагоналей), так как ромб — это частный случай дельтоида, у которого все стороны равны. Напомним, что диагональ — отрезок, соединяющий противоположные вершины.
- Площадь = (диагональ1 х диагональ2)/2, или S = (d1 × d2)/2
- Пример: если диагонали дельтоида равны 19 см и 5 см, то площадь этого дельтоида: S = (19 х 5)/2 = 47,5 квадратных сантиметров.
- Если вы не знаете длины диагоналей и не можете их измерить, используйте тригонометрию, чтобы вычислить их. Прочтите эту статью, чтобы узнать больше информации.
-
3
Найдите площадь дельтоида, используя неравные стороны и угол между ними. Если вы знаете неравные стороны и угол между этими сторонами (θ), то площадь дельтоида вычисляется с помощью тригонометрии по формуле:[4]
- Площадь = (сторона1 х сторона2) х sin (угол), или S = (a × b) × sin(θ), где θ — угол между неравными сторонами.
- Пример: Если стороны дельтоида равны 4 см и 6 см, а угол между ними равен 120 градусам, то площадь дельтоида равна (6 х 4) х sin120 = 24 х 0,866 = 20,78 квадратных сантиметров.
- Обратите внимание, что вы должны использовать две неравные стороны и угол между ними; если вы используете две равные стороны и угол между ними, вы получите неправильный ответ.
Реклама
-
1
Если вам дан четырехугольник произвольной формы, то даже для таких четырехугольников существуют формулы для вычисления их площадей. Обратите внимание, что такие формулы требуют знания тригонометрии.
- Во-первых, найдите длины всех четырех сторон. Обозначим их через a, b, c, d (а напротив с, а b напротив d).
- Пример: дан четырехугольник произвольной формы со сторонами 12 см, 9 см, 5 см и 14 см.
-
2
Найдите угол А между сторонами а и d и угол С между сторонами b и с (вы можете найти любые два противолежащих угла).
- Пример: в нашем четырехугольнике А = 80 градусов и C = 110 градусов.
-
3
Представьте, что существует отрезок, соединяющий вершины, образованные сторонами а и b и сторонами с и d. Этот отрезок разделит четырехугольник на два треугольника. Так как площадь треугольника равна 1/2absinC, где C — угол между сторонами a и b, вы можете найти площади двух треугольников и сложить их, чтобы вычислить площадь квадрата.
- Площадь = 0,5 х сторона1 х сторона4 х sin(угол между стороной1 и стороной4) + 0,5 х сторона2 х сторона3 х sin(угол между стороной2 и стороной3), или
- Площадь = 0,5 a × d × sin A + 0,5 × b × c × sin C
-
Пример: вы нашли стороны и углы, поэтому просто подставьте их в формулу.
-
- = 0,5 (12 × 14) × sin (80) + 0,5 × (9 × 5) × sin (110)
- = 84 × sin (80) + 22,5 × sin (110)
- = 84 × 0,984 + 22,5 × 0,939
- = 82,66 + 21,13 = 103,79 квадратных сантиметров.
-
- Обратите внимание, что если вы пытаетесь найти площадь параллелограмма (у которого противоположные углы равны), то формула примет вид: площадь = 0.5*(ad + bc) * sin A
Реклама
Советы
-
Этот калькулятор для вычисления площади треугольника пригодится вам при вычислении площади четырехугольника произвольной формы.[5]
- Чтобы получить дополнительную информацию, прочитайте статьи по вычислению площади квадрата, площади прямоугольника, площади ромба, площади трапеции и площади дельтоида.
Реклама
Об этой статье
Эту страницу просматривали 440 328 раз.
Была ли эта статья полезной?
Дельтоид
Материал из Большого Справочника
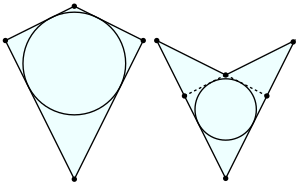
На чертеже слева дельтоид выпуклый, справа — невыпуклый.
Дельто́ид (от др.-греч. δελτοειδής — «дельтовидный», напоминающий заглавную букву дельта) — четырёхугольник, в котором есть две пары смежных равных сторон.
Свойства
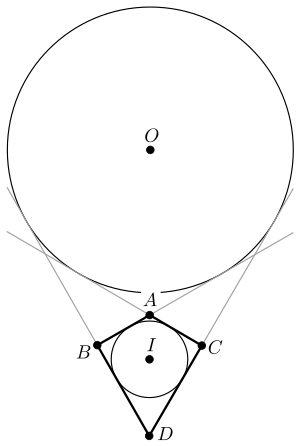
Вписанная и вневписанная окружности выпуклого дельтоида 
- Углы между сторонами неравной длины равны.
- Диагонали взаимно перпендикулярны.
- В любой выпуклый дельтоид можно вписать окружность; кроме того, если дельтоид не является ромбом, то существует ещё одна окружность, касающаяся продолжений всех четырёх сторон (см. рисунок).
- Для любого невыпуклого дельтоида можно построить окружность, касающуюся двух бо́льших сторон и продолжений двух меньших сторон, и окружность, касающуюся двух меньших сторон и продолжений двух бо́льших сторон.
- Точка пересечения диагоналей делит одну из них пополам.
- Другая диагональ является биссектрисой углов.
- Одна диагональ делит дельтоид на два равных треугольника.
- Другая диагональ делит дельтоид на два равнобедренных треугольника, если он выпуклый, и достраивает его равнобедренным треугольником до равнобедренного треугольника, если он невыпуклый.
Площадь дельтоида
- Здесь приведены формулы, свойственные именно дельтоиду. См. также формулы для площади произвольных четырёхугольников.
, где
и
— длины диагоналей.
, где
и
— длины неравных сторон, а
— угол между ними.
Частные случаи
- Если угол между неравными сторонами дельтоида прямой, то вокруг него можно описать окружность (вписанный дельтоид).
- Если пара противоположных сторон дельтоида равна, то такой дельтоид является ромбом.
- Если пара противоположных сторон и обе диагонали дельтоида равны, то дельтоид является квадратом. Квадратом является и вписанный дельтоид с равными диагоналями.
Разное
- Дельтоидами являются грани дельтоидального икоситетраэдра, дельтоидального гексеконтаэдра и трапецоэдра.
См. также
Муниципальное общеобразовательное учреждение
Малодубенская средняя общеобразовательная школа №7
Итоговый проект по геометрии
Тема: «Неизвестный дельтоид»
Обучающейся 9 класса
Романовой Ирины Александровны
Руководитель проекта:
учитель математики
Романова Людмила Геннадьевна
г.о. Орехово-Зуево
2019 г.
Оглавление
Введение 3
Определение. 4
Свойства. 4
Первое свойство. 4
Второе свойство. 4
Третье свойство. 5
Четвертое свойство. 5
Пятое свойство. 5
Признаки. 6
Первый признак. 6
Второй признак. 6
Площадь дельтоида. 7
Первая формула. 7
Вторая формула. 7
Третья формула. 8
Четвертая формула. 8
Окружность, вписанная в дельтоид. 9
Окружность, описанная около дельтоида. 9
Теорема 1. 9
Теорема 2. 10
Теорема 3. 10
Примеры решения задач. 11
Задача 1. 11
Задача 2. 11
Задача 3. 12
Задача 4. 12
Заключение. 13
Список используемой литературы. 14
Введение
Существуют различные виды классификаций четырехугольников, например, по параллельности сторон выделяют параллелограмм, у которого попарно параллельны все стороны, и трапецию — параллельны две стороны, по равенству сторон выделяют ромб и квадрат, по равенству всех углов – квадрат и прямоугольник и т.д., эти фигуры изучаются в школьной программе.
Изучая литературу, решая геометрические задачи, я обратила внимание на то, что четырехугольник, у которого диагонали перпендикулярны, но не является ромбом, обладает рядом интересных свойств. Этот четырехугольник – дельтоид.
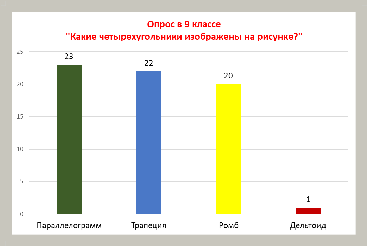
В своем классе я провела опрос по определению геометрических фигур: трапеция, параллелограмм, ромб и дельтоид. Участие приняли 25 человек. Результаты опроса отображены на диаграмме.
Поэтому целью моего проекта является: изучить дельтоид и рассмотреть применение его в окружающем мире.
Для выполнение этой цели были поставлены следующие задачи:
-
Дать определение дельтоида.
-
Изучить свойства и признаки дельтоида.
-
Рассмотреть задачи, которые решаются с дельтоидом.
-
Найти практическое применение.
Определение.
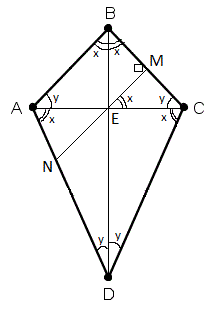
Дельтоид – четырехугольник, обладающий двумя парами смежных сторон одинаковой длины, диагонали пересекаются под прямым углом. Дельтоид иначе называют ромбоидом. Название дельтоид происходит от названия греческой буквы (дельта).
|
Выпуклый дельтоид |
Невыпуклый дельтоид |
Свойства.
Первое свойство.
У дельтоида одна пара противолежащих углов равна. (Углы, лежащие по разные стороны от главной диагонали равны.)
|
|
Дано: ABCD – дельтоид Доказать: /BAD = /BCD Решение:
Значит /BAC = /BCA
Значит /CAD = /ACD
/BCD = /BCA + /DCA Значит /BAD = /BCD |
Второе свойство.
Большая диагональ является биссектрисой.
|
|
Дано: ABCD – дельтоид Доказать: BD – биссектриса Док-во: 1) ∆BAD = ∆BCD (по 1 призн), т.к. AB = CB, AD = CD, /BAD = /BCD 2) /ABD = /CBD /ADB = /CDB 3) BD – биссектриса. |
Третье свойство.
Диагонали дельтоида пересекаются, и точкой пересечения меньшая диагональ делится пополам.
|
|
Дано: ABCD – дельтоид Доказать: AO=CO Док-во: 1) т.к. ∆BAD = ∆BCD (аналогично в 1 свойству) 2) AO – высота ∆BAD, CO – высота ∆BCD (диагонали BD┴AC) 3) высоты равных треугольников тоже равны AO=CO |
Четвертое свойство.
Осью симметрии дельтоида является большая диагональ.
|
|
Дано: ABCD – дельтоид Доказать: BD – ось симметрии Док-во: 1) рассмотрим симметрию относительно BD. 2) точка D перейдет в саму себя. 3) точка A перейдет в точку C, т.к. AO = OC и BD|AC 4) точка B перейдет в саму себя 5) точка C перейдет в точку A, т.к. AO = OC и BD|AC 6) ∆BAD перейдет в ∆BCD 7) BADC — BCDA |
Пятое свойство.
Параллелограммом Вариньона, построенный в серединах сторон дельтоида, является прямоугольник.
|
|
Дано: ABCD – дельтоид Найти: определить вид четырехугольника KLMN Решение: 1) рассмотрим ∆BAD, KN — средняя линия, KN||BD, KN=12BD. 2) рассмотрим ∆BCD, LM — средняя линия, LM||BD, LM=12BD. 3) KN||LM, KN=LM. 4) так как BD|AC, то KN|NL, LM|KM. 5) KLMN- прямоугольник |
Признаки. Первый признак.
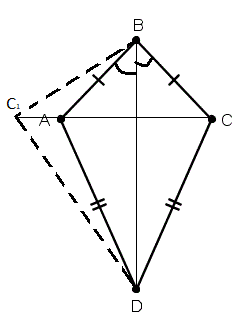
Теорема 1. Если одна из диагоналей четырехугольника является биссектрисой одного из его углов и делит периметр четырехугольника пополам, то четырехугольник есть дельтоид.
|
|
Дано: ABCD — четырехугольник BD — биссектриса /ABD PBCD=PBAD Доказать: ABCD — дельтоид |
Доказательство: (от противного)
-
Предположим, что A и C – не симметричны, относительно BD.
-
Построим C1, симметричную точке C (C1 = A).
-
Так как периметры равны, т.е. PBCD=PBAC=PBC1D, то приходим к противоречию. Значит A-C1
-
ABCD – дельтоид.
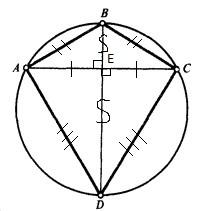
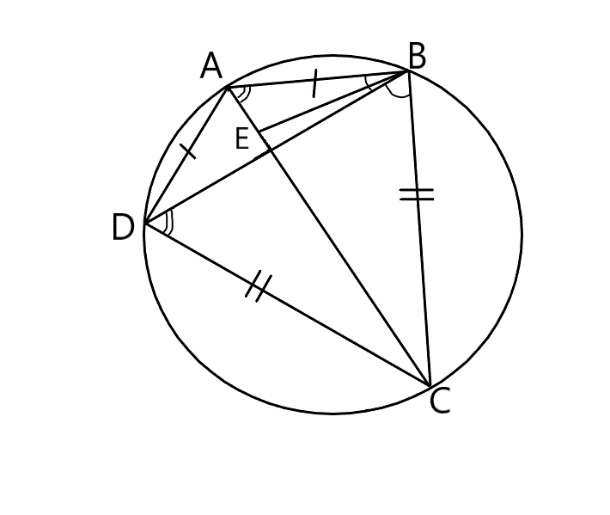
Второй признак.
Теорема 2. Если у четырехугольна, вписанного в окружность, ось симметрии совпадает с диагональю, то он является дельтоидом.
|
|
Дано: ABCD — четырехугольник Окружность (O, R) – описанная BD – диагональ = ось симметрии Доказать: ABCD — дельтоид |
Доказательство:
-
Т.к. BD — ось симметрии, то A-C, значит AC-BD
-
∆ABE = ∆CBE (по 1 признаку: AE=CE, BE – общая, /BEA=/BEC=90), значит AB=BC
-
∆AED = ∆CED (по 1 признаку: AE=CE, DE – общая, /AED=/CED=90), значит AD=CD
-
ABCD – дельтоид
Площадь дельтоида. Первая формула.
S= 1/2d1d2
|
|
BD=d1, AC=d2. S=SABO+SCBO+SADO+SCDO SABO= 1/2AO*BO SCBO= 1/2BO*CO SADO= 1/2AO*DO SCDO= 1/2CO*DO S= 1/2AO*BO + 1/2BO*CO + 1/2AO*DO + 1/2CO*DO= =1/2BO(AO+CO)+1/2BO*AC+1/2DO*AC= =1/2AC(BO+DO)= 1/2AC*BD=1/2d1*d2 |
Вторая формула.
Известным индийским математиком Брахмагуптой (около 598 года н.э.) было установлена формула площади вписанного в окружность четырехугольника, а именно:
S=√(p-a)(p-b)(p-c)(p-d), где p=(a+b+c+d)/2 – полупериметр четырехугольника. Эта формула является обобщенным случаем известной формулы площади треугольника.
Применим данную формулу для вписанного в окружность дельтоида. Так как a=b и c=d получаем, что S=(p-a)(p-b). Докажем это.
S=(p-a)(p-b) или S=ab, т.к. P=(2a+2b)/2=a+b.
|
|
1) По теореме косинусов AC2= a2+ a2-2a2 *cos /B= = b2+ b2-2b2 *cos /D. AC2= 2a2+ 2a2-2a2 *cos /B= 2b2+ 2b2-2b2 *cos /D. 2) Т.к. ABCD – вписанный четырехугольник, то /D=1800—/B, поэтому cos /D= -cos /B, sin /D=sin /B, следовательно, 2a2-2a2 *cos /B= 2b2-2b2 *cos /D. 2(a2-b2) = 2cos /B(a2+b2) a2-b2 = (a2+b2) cos /B (1) Площадь четырехугольника равна сумме площадей треугольников, на который он разбивается своей диагональю, то есть S = 1/2*a2*sin /B+1/2*b2*sin /D = ½ (a2 + b2) sin /B или 2S = (a2 + b2) sin /B (2) Возведем неравенства (1) и (2) в квадрат и сложим их, учитывая, что cos2 /B + sin2 /B = 1, получим 4S2 + (a2 — b2)2 = (a2 + b2)2 4S2 = (a2 + b2)2 — (a2 — b2)2 4S2 = (a2 + b2 — a2 + b2) (a2 + b2 + a2 — b2) 4S2 = 2a2 * 2b2 S2 = a2 * b2 S = ab Это доказательство проводилось по рассуждениям древнего математика Брахмагупты, эту же формулу можно вывести короче: |
Т.к. дельтоид вписан в окружность, то большая диагональ является диаметром, значит она разбивает четырехугольник на два равных прямоугольных треугольника (вписанный угол, опирающийся на диаметр равен 90⸰). Площадь прямоугольного треугольника равна S=12ab, значит площадь дельтоида равна S=ab.
Третья формула.
Площадь вписанного дельтоида можно найти другим способом. Докажем теорему: если дельтоид со сторонами a, b, вписан в окружность радиуса R, то его площадь равна
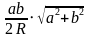
Доказательство:
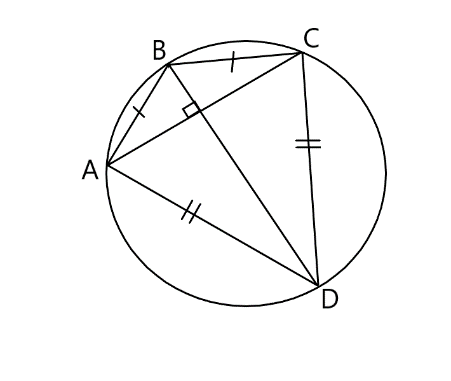
Пусть диагонали дельтоида равны x и y.
SABCD = SABC + SACD или SABCD = SBCD + SABD.
Воспользовавшись формулой S= abc/4R, где a,b,c, — стороны треугольника, а R- радиус описанной окружности, получаем:
SABCD = abx/2R (1) или SABCD = a2y/4R+ b2y/4R (2)
Перемножив неравенства (1) и (2), получаем:
SABCD = abx/2R*(a2y/4R+ b2y/4R) = 1/8R2* ab(a2+b2) * xy = 1/8R2* 2a2b2(a2 + b2) = 1/4R2* a2b2(a2 + b2) (так как по теореме Птолемея xy = ac+bd, то есть xy = 2ab), значит S = 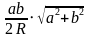
Четвертая формула.
Площадь параллелограмма Вариньона равна половине площади дельтоида.
|
|
Докажем, что SKLMN=12SABCD SABCD=12d1*d2 SKLMN= KL*LM=12d1*12d2= 12 SABCD, так как KL – средняя линия треугольника ABC и LM – средняя линия треугольника BCD. |
Окружность, вписанная в дельтоид.
Докажем, что в дельтоид можно вписать окружность.
Доказательство:
|
|
В четырехугольник можно вписать окружность, если суммы противолежащих сторон равны. Действительно, т.к. AB=BC и CD=AD, то AB+CD=BC+AD. |
Окружность, описанная около дельтоида.
Теорема 1.
В дельтоиде ABCD через точку пересечения диагоналей проведена прямая, перпендикулярная к одной из сторон. Доказать, что если эта прямая делит другую сторону пополам, то дельтоид можно вписать в окружность.
|
|
Доказательство: Пусто прямая NM пересекает сторонe BC под прямым углом, а сторону AD делит пополам. Тогда /EMB=/MEC=/NAE, а это значит, что утверждение доказано. ABC/2x+2y=180 /ABC+/ADC=/BAD+/BCD= 2x+2y=180⸰ |
Утверждение: если четырехугольник является вписанным, то центр описанной около него окружности – точка пересечения серединных перпендикуляров к сторонам четырехугольника.
В самом деле, серединный перпендикуляр к отрезку содержит все точки, равно удаленные от концов этого отрезка, следовательно, точка пересечения серединных перпендикуляров вписанного в окружность четырехугольника, равно удалена от вершин этого четырехугольника, т.е. от некоторых точек окружности.
По определению центра окружности, из этого следует, что данная точка – центр описанной около этого четырехугольника окружности.
Теорема 2.
Вписанный дельтоид является примером гармонического четырехугольника (вписанный четырехугольник с перпендикулярными диагоналями, произведение длин противоположенных сторон которого равны)
Вписанный в окружность четырехугольник обладает рядом интереснейших свойств. Одно из них было доказано древнегреческим математиком и астрономом Клавдием Птолемеем (около 100 – 178 г. н. э.) в его знаменитом сочинении «Альмагест» (астрономы в странах арабского Востока называли эту книгу «Альмаджисти» — «Величайшие», отсюда и происходит её название «Альмагест»).
Теорема, носящая имя Птолемея: произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон.
|
|
Т.к. у дельтоида две пары равных соседних сторон, то утверждение выглядит так: d1*d2=2a*b Докажем это: |
Возьмём на диагонали AC точку E так, что /ABE = /DBC. Тогда ∆ABE и ∆DBC подобны, т.к. /BAE = /BAC= /BDC. Поэтому 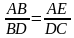
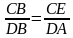
то есть d1*d2 = 2a*b
Теорема доказана.
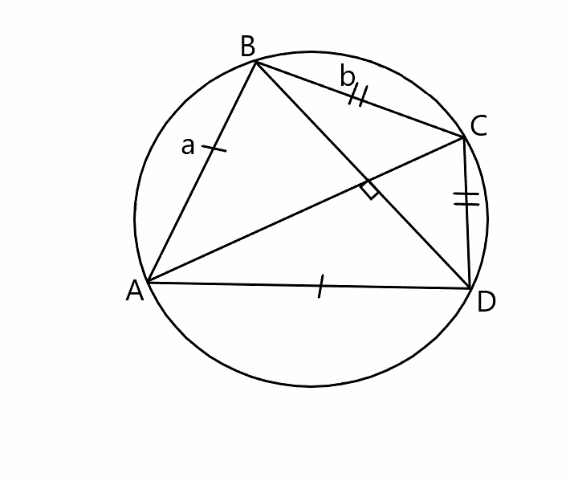
Теорема 3.
Сумма квадратов неравных сторон равна учетверённому квадрату радиуса описанной окружности.
|
Докажем его.
|
Рассмотрим вписанный в окружность четырехугольник ABCD, диагонали которого перпендикулярны. В нём AB=a, BC=b, CD=c, AD=a, а радиус описанной окружности равен R. Докажем, что Обозначим BD как d1, AC как d2, /ABD как /1, /BAC как /2, /CAD как /3, /ADB как /4, тогда /BCA=/4 ( т.к. опирается с /ADB на одну дугу), аналогично /BCA=/4, /CBD=/3, /BDC=/2, /ACD=/1. По теореме синусов получаем: a = 2R*sin /2, b = 2R*sin /1 (так как /2 = 90⸰ — /1), из этого a2 + b2 = 4R2 sin /1 + 4R2 cos /1 = 4R2, следовательно, a2 + b2 = 4R2 Свойство доказано. |
Примеры решения задач.
Выше мы рассмотрели общие свойства дельтоида. Также свойства некоторых особых видов таких четырехугольников.
Теперь решим несколько задач, в которых встречается данный четырехугольник.
Задача 1.
В дельтоиде средние линии пересекаются на оси симметрии дельтоида.
|
|
Доказательство: Пусть K, L, M, N – середины сторон дельтоида. Поскольку KLMN – прямоугольник, то его диагонали пересекаются на оси симметрии BD. |
Задача 2.
В дельтоид вписана окружность, которая касается равных сторон в точках M и N, P и Q. Определить вид четырехугольника MNPQ.
|
Решение: Пусть ABCD — данный четырехугольник. Поскольку BM=BN, то MN||AC. Аналогично QP||AC. Поскольку QM=NP, то четырехугольник – равнобедренная трапеция. |
Задача 3.
Построить дельтоид ABCD по сторонам a, b и углу между равными сторонами y.
|
План построения:
|
Задача 4.
Найдите площадь дельтоида ABCD, у которого AB=a, AD=b, AC=d.
|
|
Решение:
|
Заключение.
В данной работе было рассмотрено что такое дельтоид, какими свойствами должен обладать четырехугольник, чтобы его можно было назвать дельтоидом. В заключении работы было разобрано несколько задач.
Но это далеко не всё, что может быть изучено по теме «Дельтоид».
Если посмотреть на карту неба, то мы можем обнаружить знакомую нам фигуру. Четыре самые яркие образуют ромбоид – характерную геометрическую фигуру созвездия Весы. В окружающем мире дельтоид встречается в конструировании воздушных змеев и летательных аппаратов, плавательных судов, а также в области биологии: крона дерева туя, лист березы, тело рыбы, форма носа, соединенные пальцы человека и др.
В качестве направлений для дальнейших исследований проект предполагает рассмотреть свойства аналогичных фигур и в стереометрии.
Расширить представленную в проекте тему можно изучением применения свойств дельтоида в оригами (Оригами – наглядная модель евклидовой геометрии)
Список используемой литературы.
-
Журнал «Квант» №2, 1992 г. http://kvant.mccme.ru/1992/02/p37.htm
-
Журнал «Квант» №10, 1991 г. http://kvant.mccme.ru/1991/10/p48.htm
-
И.Л. Никольская «Факультативны курс математике 7-9».
-
В.В. Прасолов «Задачи по планиметрии».
-
И.Ф. Шарыгин «Геометрия (планиметрия) 7-9».
-
В.А. Гусев, В.Н. Литвиненко, А.Г. Мордкович «Практикум по элементарной математике (геометрия)».
-
Картинка дельтоид https://yandex.ru/images/search








































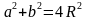 .
.