Как найти площадь девятиугольника 4 класс - Исправление недочетов и поиск решений вместе с Examum.ru

Правильный девятиугольник

Материал из Большого Справочника

Правильный девятиугольник

Правильный девятиугольник — это правильный многоугольник с девятью сторонами.

Свойства

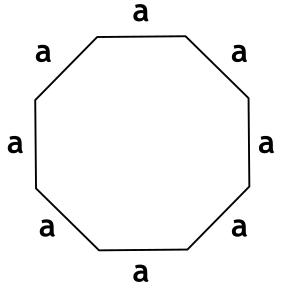
Правильный девятиугольник имеет внутренние углы, равные 140°. Площадь правильного девятиугольника со стороной a определяется выражением

$S={frac {9}{4}}a^{2}cot {frac {pi }{9}}simeq 6.18182,a^{2}.$

Построение

Хотя правильный девятиугольник и невозможно построить с помощью циркуля и линейки, существуют методы построения достаточно точных приближений.

Девятиугольные звёзды

Существует три звёздчатых девятиугольника: {9/2}, {9/3} и {9/4}, причём звезда {9/3} состоит из трёх равносторонних треугольников:

См. также

Источник

На странице собраны калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного многоугольника по стороне и количеству сторон, а также зная радиус вписанной и описанной окружностей.

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

Содержание:

калькулятор площади правильного многоугольника
формула площади правильного многоугольника через длину стороны
формула площади правильного многоугольника радиус вписанной окружности
формула площади правильного многоугольника радиус описанной окружности
пример задачи

Формула площади правильного многоугольника через длину стороны и число сторон

S = dfrac{na^2}{4} cdot ctg dfrac{180°}{n}

a — длина стороны многоугольника

n — число сторон многоугольника

Формула площади правильного многоугольника через радиус вписанной окружности

S = nr^2 tg dfrac{180°}{n}

r — радиус вписанной в многоугольник окружности

n — число сторон многоугольника

Формула площади правильного многоугольника через радиус описанной окружности

S = dfrac{nR^2}{2} cdot sin dfrac{360°}{n}

R — радиус описанной в многоугольник окружности

n — число сторон многоугольника

Пример задачи на нахождение площади правильного многоугольника

Задача 1

Найдите площадь правильного n-угольника, если n = 6, r = 9 см, где r — радиус вписанной окружности.

Решение

Чтобы решить эту задачу мы используем вторую формулу.

S = nr^2 tg dfrac{180°}{n} = 6 cdot 9^2 cdot tg dfrac{180°}{6} = 6 cdot 81 cdot tg 30° = 486 cdot tg 30° = 486 cdot 0.57735027 approx 280.59223 : см^2

Ответ: 486 cdot tg 30° approx 280.59223 : см^2

Чтобы проверить ответ воспользуемся калькулятором .

Источник

Вычисление девятиугольника (фигура с девятью вершинами). Введите одно известное значение, затем нажмите кнопку вычислить.

Поделиться расчетом:

Калькулятор девятиугольника, введите одно известное значение

Длина стороны(a)

Меньшая диагональ(d1)

Средняя диагональ(e)

Большая диагональ(d3)

Высота(h)

Периметр(p)

Площадь(S)

Радиус описанной окружности(R)

Радиус вписанной окружности(r)

Вычислить

Очистить

Формулы:

a = 2 * R * sin( π / 9 )
d = 2 * R * sin( 2 * π / 9 )
e = 2 * R * sin( 3 * π / 9 )
f = 2 * R * sin( 4 * π / 9 )
h = R + r
p = 9 * a
S = 9/2 * R * sin( 2 * π / 9 )
r = a / 2 * tan( π / 9 )
Угол: 140°, 27 диагоналей.

Источник

Найти площадь правильного 9 — тиугольника если его сторона равна 4см.

На странице вопроса Найти площадь правильного 9 — тиугольника если его сторона равна 4см? из категории Геометрия вы найдете
ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не
устраивает и нужно расшить круг поиска, используйте удобную поисковую
систему сайта. Можно также ознакомиться с похожими вопросами и ответами
других пользователей в этой же категории или создать новый вопрос. Возможно,
вам будет полезной информация, оставленная пользователями в комментариях, где
можно обсудить тему с помощью обратной связи.

Источник

Правильный девятиугольник

Площадь правильного девятиугольника — это число, характеризующее девятиугольник в единицах измерения площади.

Правильный девятиугольник — это девятиугольник у которого все стороны и углы равны.

Содержание

1 Обозначения
2 Формулы:
- 2.1 n=9:
3 Другие многоугольники:
4 Ссылки

Обозначения

Введём обозначения:

a — длина стороны;

n — число сторон, n=9;

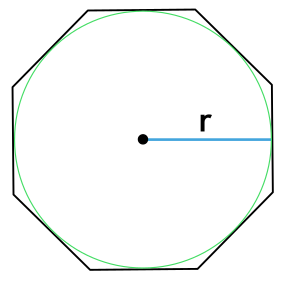
r — радиус вписанной окружности;

R — радиус описанной окружности;

α — половинный центральный угол, α=π/9;

P₉ — периметр правильного девятиугольника;

S_Δ — площадь равнобедренного треугольника с основанием равным стороне и боковыми сторонами равными радиусу описанной окружности;

S₉ — площадь правильного семиугольника.

Формулы:

n=9:

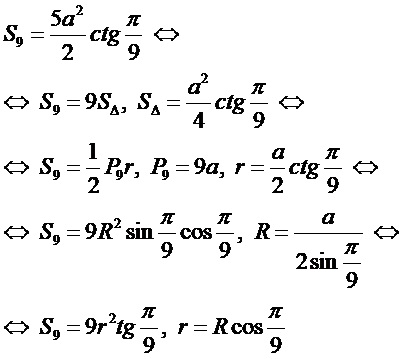
Другие многоугольники:

Ссылки

Участник:Logic-samara

Источник