Добрый день. Правильно ли я решила задачу?
Плоский конденсатор имеет емкость С=330пФ, определить площадь пластин и толщину диэлектрика из слюды. Номинальное напряжение конденсатора U=1500 B, и он должен иметь четырехкратный запас прочности по напряжению(6кВ)
Система СИ: 330пФ = 0,0000033 Ф
6кВ= 6000 В
Решение
С=е* e0*S/d; e0=8,85*10^-12
E0 – электрическая постоянная
S – площадь пластин конденсатора
D – толщина диэлектрика
E=U/d => d=U/E=1500 B/6000 B=0,25 B
S=C*d/e*e0 = 0,0000033 Ф *0,25 В / 8,85*10^-12*6000 = 15,54
| Комментарий модератора | ||
|
Площадь пластины (обкладки) в плоском конденсаторе. Калькулятор онлайн.
Онлайн калькулятор вычисления площади пластины (обкладки) в плоском конденсаторе, позволит найти площадь пластины (обкладки) через электроёмкость и расстояние между пластинами, а также через расстояние между пластинами, напряжение и заряд на пластине. Калькулятор произведет вычисление и даст подробное решение. Единицы измерения, могут включать любые приставки Си. Калькулятор автоматически переведет одни единицы в другие.
Калькулятор содержит:
Площадь пластины (обкладки) в плоском конденсаторе через электроёмкость и расстояние между пластинами.
Площадь пластины (обкладки) в плоском конденсаторе через расстояние между пластинами, напряжение и заряд на пластине.
Площадь пластины (обкладки) в плоском конденсаторе через электроёмкость и расстояние между пластинами
Плоский конденсатор представляет собой две параллельные проводящие пластины, разделенные диэлектриком, расположенные на малом расстоянии друг от друга.
Площадь пластины (обкладки) в плоском конденсаторе через электроёмкость и расстояние между пластинами определяется формулой, где
ε0 – электрическая постоянная, ε0 = 8.85418781762039 × 10-12
ε – диэлектрическая проницаемость диэлектрика
C — емкость плоского конденсатора
d — расстояние между пластинами
Единица измерения площади является — Метр квадратный (м2, m2).
Диэлектрическая проницаемость ε =
Электроемкость C
Расстояние между пластинами d =
Единица измерения площади S
Площадь пластины (обкладки) в плоском конденсаторе через расстояние между пластинами, напряжение и заряд на пластине
Плоский конденсатор представляет собой две параллельные проводящие пластины, разделенные диэлектриком, расположенные на малом расстоянии друг от друга.
Площадь пластины (обкладки) в плоском конденсаторе через расстояние между пластинами, напряжение и заряд на пластине определяется формулой, где
ε0 – электрическая постоянная, ε0 = 8.85418781762039 × 10-12
ε – диэлектрическая проницаемость диэлектрика
Q — заряд на пластине
d — расстояние между пластинами
U — напряжение
Единица измерения площади является — Метр квадратный (м2, m2).
Диэлектрическая проницаемость ε =
Заряд Q =
Расстояние между пластинами d =
Напряжение U =
Единица измерения площади S
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Практические задания
1. Определение параметров воздушного конденсатора.
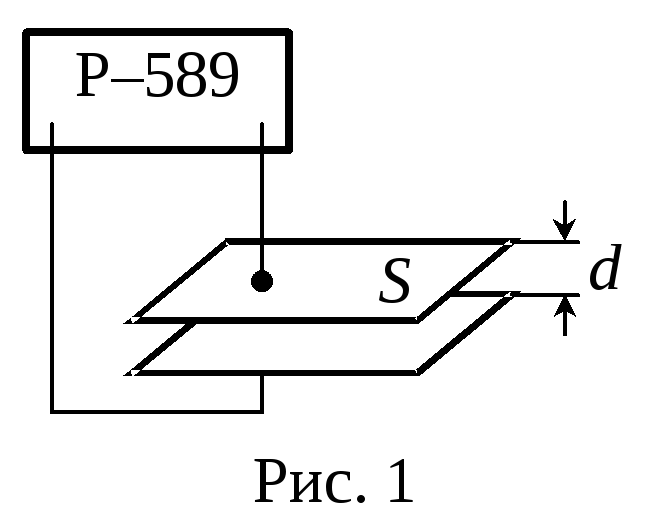
Д
ля выполнения дальнейших расчетов
необходимо знать площадь пластин
конденсатораSи расстояние между
нимиd(Рис. 1). Определение площади
не вызывает затруднений, достаточно
измерить длину и ширину пластин и
рассчитать площадьS. Для определения
расстояния между пластинами конденсатора
с необходимой точностью приходится при
помощи моста переменного тока определить
емкость конденсатораC0и рассчитать расстояние между пластинами
по формуле:
.
2. Определение емкости плоского конденсатора с диэлектрической пластиной и расчет диэлектрической проницаемости.
П
33
лоский конденсатор с диэлектрической
пластиной можно представить в виде
эквивалентной схемы, содержащей три
конденсатора, соединенные так, как
показано на (Рис. 2). Результирующая
емкость такого конденсатора может быть
рассчитана по формуле:
,
и может быть
измерена экспериментально. Емкость
каждого из конденсаторов эквивалентной
схемы можно определить теоретически
по приведенным выше формулам:
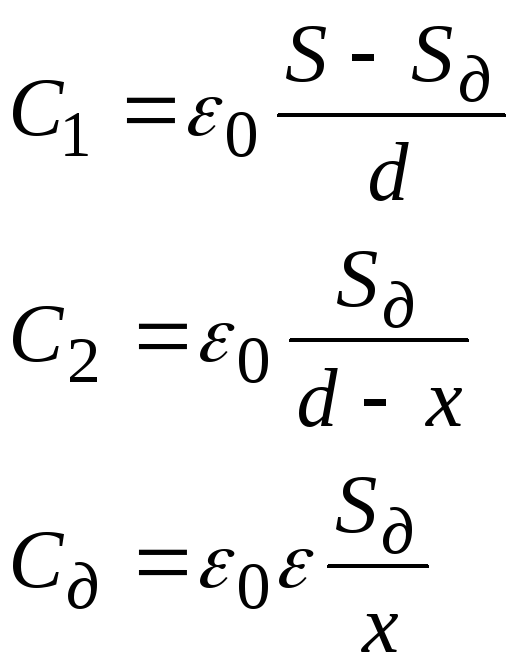
где Sдиx– площадь и толщина диэлектрической
пластины.
Далее, из формулы
полной емкости выводится формула для
расчета емкости конденсатора с
диэлектриком Cд:
,
куда подставляются
рассчитанные емкости C1,C2и
измеренная емкостьC, после чего
определяется диэлектрическая проницаемость
диэлектрика:
.
Определить
диэлектрическую проницаемость всех
предложенных в работе диэлектриков и
проанализировать их сравнительную
способность поляризоваться во внешнем
электрическом поле.
Вопросы к зачету по работе.
-
Чем отличаются
неполярные диэлектрики от полярных? -
В чем заключается
физический механизм поляризации
диэлектриков? -
Чему равна общая
емкость последовательно и параллельно
соединенных конденсаторов? -
Как рассчитать
емкость смешанного соединения
конденсаторов? -
Ч
34
то характеризует диэлектрическая
проницаемость диэлектрика?
Лабораторная работа
№ 8
Изучение
электронно-лучевого осциллографа
Цель
работы.
Изучить устройство,
принцип действия, возможности и рабочие
характеристики электронно-лучевого
осциллографа С1-83.
Знания,
необходимые для допуска к работе.
-
Закономерности
движения заряженных частиц в электрическом
поле; -
Устройство и
органы управления электронно-лучевого
осциллографа;
Краткие
сведения из теории.
Электронный
осциллограф является универсальным
электроизмерительным прибором,
позволяющим изучать быстропеременные
процессы, снимать зависимости электрических
величин от времени и одних электрических
величин от других. Кроме того, осциллограф
дает возможность изучать неэлектрические
процессы при использовании преобразователей
неэлектрических величин в электрические.
Так как в осциллографе используется
электронный луч, осциллограф обладает
высокой чувствительностью и практическим
отсутствием инерционности.
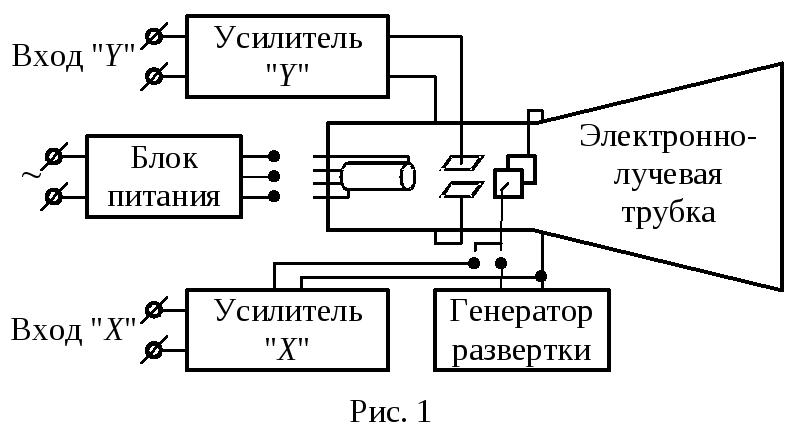
О
сциллограф состоит из
следующих основных блоков (Рис. 1):
-
электронно-лучевая
трубка (ЭЛТ) с органами управления
лучом; -
блок управления
канала вертикального отклонения луча
(«Y«); -
блок управления
канала горизонтального отклонения
луча («X«); -
генератор временной
развертки, включающий блок синхронизации; -
б
35
лок питания (трансформатор и
выпрямитель).
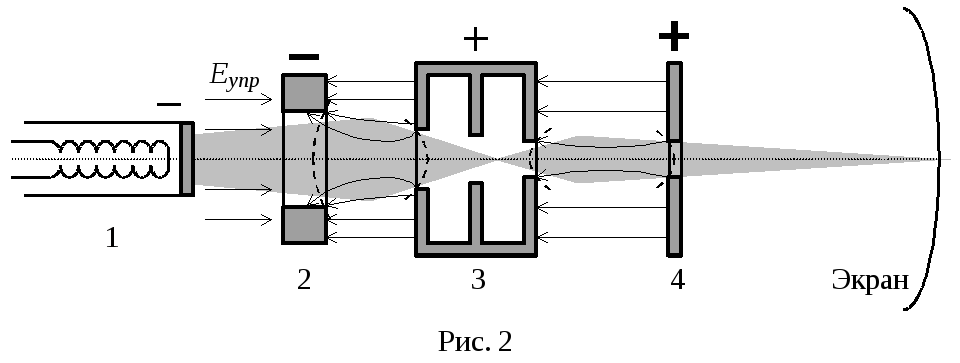
Э
36
лектронно-лучевая трубка представляет
собой стеклянную, откачанную до высокого
вакуума колбу с находящимися внутри
электронной пушкой, отклоняющими
пластинами и экраном, покрытым
флюоресцирующим веществом (Рис. 2).
Электронная пушка служит для создания
тонкого пучка электронов (электронного
луча) и состоит из подогреваемого катода
«1», управляющего электрода «2»,
первого (фокусирующего) «3» и второго
(ускоряющего) «4» анодов. При
нагревании катода вылетающие из него
электроны попадают в ускоряющее
электрическое поле, созданное подачей
разности потенциалов порядка 15
кВ между катодом и вторым анодом. На
пути электронов располагается управляющий
электрод, на который подается отрицательный
по отношению к катоду потенциал. Изменяя
величину этого потенциала можно
электрическим полем Еупр
регулировать количество электронов,
вылетающих из катода, и, тем самым,
управлять яркостью свечения картинки
на экране трубки. Далее электроны
попадают в область неоднородного поля
вблизи отверстий между управляющим
электродом и первым анодом, действующую
как собирающая линза. Расходящийся
электронный пучок собирается в точку
вблизи первого анода. Первый анод
представляет собой цилиндр, состоящий
из нескольких диафрагм, выделяющих из
всего потока электронов более тонкий
пучок, который далее фокусируется полем
в области между первым и вторым анодом
и образует четкую картинку на экране.
Меняя величину потенциала на первом
аноде, можно менять «фокусное
расстояние» системы анодов, и,
соответственно, настраивать фокусировку
изображения.
Блок управления
канала «Y»
состоит из входного ступенчатого
делителя напряжения с плавным
потенциометром (реохордом), собственно
усилителя исследуемого сигнала, а также
системы смещения луча по вертикальной
оси, представляющей собой потенциометр
««,
с которого подается разность потенциалов
на пластины вертикального отклонения
луча. Так как на электрон, пролетающий
между пластинами, действует сила,
он будет отклоняться от прямолинейной
траектории, и угол отклонения (смещение
луча по оси) будет пропорционален
разности потенциалов на пластинах,
где
y
– чувствительность трубки по оси «Y«.
Зная
y,
можно производить измерения напряжения
uy
по величине отклонения луча, но в
современных осциллографах, как правило,
переключатель входного делителя
напряжения уже откалиброван в единицах
mV/деление или V/деление и знания
чувствительности не требуется.
Блок управление
каналом «Х»
в целом аналогичен блоку управления
каналом «Y«.
Он используется для снятия вольт-вольтовых
характеристик электронных приборов
или физических явлений. В этом случае
он подключается к пластинам горизонтального
отклонения луча и органы управления
усилением и смещением «»
выполняют соответствующие их названиям
функции. Измерения напряжения также
аналогичны:.
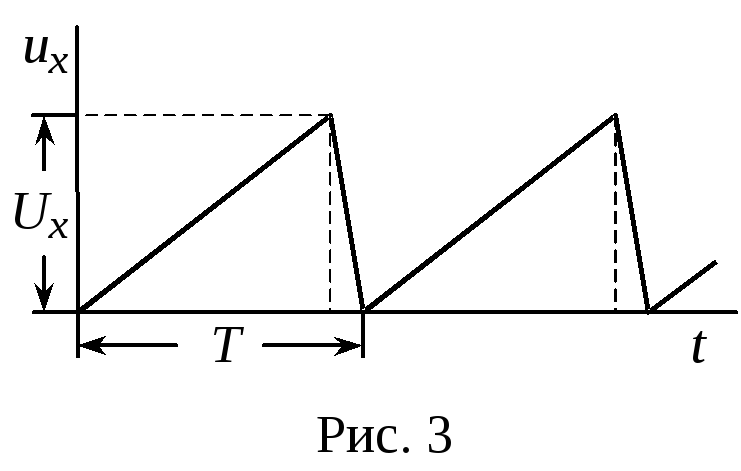
Д
37
ля снятия временных характеристик,
отражающих течение физических процессов
во времени блок управления каналом «Х»
отключается и на пластины горизонтального
отклонения с генератора временной
развертки подается сигнал специальной
формы (Рис. 3). Иногда его называют
генератором пилообразного напряжения.
Так как смещение луча пропорционально
напряжению на отклоняющих пластинах,
линейно меняющемуся со временем,
,
то луч за большую часть периода будет
равномерно смещаться по горизонтали,
а потом практически мгновенно возвращаться
в крайнее левое положение и снова
двигаться вправо. Варьируя амплитуду
пилообразного сигнала можно регулировать
горизонтальный размер осциллограммы.
Периодичность движения луча позволяет
наблюдать на экране осциллографа быстро
повторяющиеся процессы в стационарном
виде. Для этого необходимо подобрать
период развертки так, чтобы он был кратен
целому числу периодов исследуемого
сигнала или использовать режим
синхронизации, который искусственно
задерживает начало следующего периода
развертки, пока фаза исследуемого
сигнала не станет равна первоначальной.
Измерения времени по отклонению луча
по горизонтали также не представляют
сложности, так как регулятор периода
развертки, как правило, откалиброван в
единицах ms/деление илиs/деление.
В двухлучевых
осциллографах блок управления каналом
«Х»
при снятии временных характеристик
часто используется как дополнительный
блок канала «Y«,
и тогда они маркируются, соответственно,
«Y1″
и «Y2″.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
С= eeoS/d, где
е = относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (в вакууме равна единице)
ео = электрическая постоянная, численно равная 8,854187817·10 ^(-12)
d = расстояние между пластинами, d^2 Остальные ответы
С= eeoS/d, где
е = относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (в вакууме равна единице)
ео = электрическая постоянная, численно равная 8,854187817·10 ^(-12)
d = расстояние между пластинами, d^2 Остальные ответы
Не знаю как Вам, а мне никогда не нравилось работать и вычислять ёмкости конденсаторов. Больше всего раздражало наличие в исходных данных, ёмкостей в разных номиналах, в пикофарадах, в нанофарадах, микрофарадах. Их приходилось переводить в Фарады, что влекло за собой глупейшие ошибки в расчетах.
Конденсатор — в принципе это любая конструкция, которая может сохранять накопленный электрический потенциал. Если же эта конструкция, не только хранит электроэнергию, но и генерирует её, то это уже источник электропитания и никак не конденсатор.
Конструкция конденсаторов может быть любой, но чаще всего в практике используется плоский конденсатор, состоящий из двух проводящих пластин, между которыми находится какой либо диэлектрик. Это связано с тем, что расчет ёмкости такого конденсатора ведется по известной формуле и простотой его создания. Свернув такой плоский конденсатор в рулон, мы получаем, что при фактическом скромном размере «рулона», там находится плоский конденсатор, длиной в десятки сантиметров и обладающий повышенной ёмкостью.
Емкости конденсаторов некоторых форм известны, и мы дальше их рассмотрим.
Но хотелось бы заметить, что на наш взгляд, потенциал развития конденсаторов до конца не завершен. Ведь форма конструкции какого либо конденсатора может быть любая, материалы из которого сделаны обкладки или диэлектрический слой тоже могут быть любыми в пределах таблицы Менделеева. Единственная сложность, это невозможность теоретически просчитать потенциальную ёмкость, новосозданного (другой конструкции) конденсатора. Это усложняет нахождение самой лучшей конструкции конденсатора.
Есть хорошая книга по рассмотрению электрической ёмкости различных фигур. Для любопытных рекомендую поискать на просторах Интернета: Расчет электрической ёмкости в авторстве Ю.Я.Иоселль 1981 года
Данный бот рассчитывает параметры типовых форм конденсаторов. Отличие от других калькуляторов, присутствующих в интернете, это возможность задавать параметры, которые Вам известны, для того что бы рассчитать остальные.
И последнее нововведение, которое вы можете использовать. Вам не обязательно придется переводить заданные данные в метры, фарады и т.д. Достаточно обозначить размерность данных.
Например, если ёмкость известна и равно 100 пикофарад, то боту можно так и написать c=100пикофарад или с=100пФ, бот сам переведет в Фарады.
Результат, тоже будет выдан оптимально визуальному восприятию пользователя.
Это стало возможно с созданием бота Система единиц измерения онлайн
Плоский конденсатор. Параметры
| Ёмкость плоского конденсатора |
| Относительная диэлектрическая проницаемость |
| Площадь одной из обкладок конденсатора |
| Расстояние между обкладками |
| Полученные характеристики плоского конденсатора |
Самая простая и самая распространенная конструкция конденсатора это два плоских проводника разделенных тонким слоем диэлектрика ( то есть материала не проводящего электрический ток).
Ёмкость такого сооружения определяется следующей формулой.
где ε0 = 8,85.10-12 Ф/м — абсолютная диэлектрическая проницаемость
Если же конденсатор состоит не из пары пластин, а каого то n-ого количества плоских пластин то ёмкость такого «слоёного» конденсатора составит
Еще интереснее выглядит формуа такого «слоёного» конденсатора, если в слоях находятся разные диэлектрики , разной толщины d
S- площадь одной из обкладок конденсатора ( предполагаем что другая обкладка имеет такую же площадь)
d- расстояние между обкладками
С- ёмкость конденсатора
Задача: Ёмкость плоского конденсатора 350 нанофарад, расстояние между обкладками 1 миллиметр, и заполнено воздухом. Определить какова площадь обкладок?
Сообщаем боту что нам известно: C=350нФ, d=1мм. Так как у воздуха диэлектрическая проницаемость 1.00059 то e=1.00059. Поле площадь очистим, так именно его мы будем определять
Получаем вот такой ответ
| Полученные характеристики плоского конденсатора |
Ответ, площадь обкладок конденсатора при таких значениях должна составлять почти 40 квадратных метров.
Цилиндрический КОНДЕНСАТОР
| Ёмкость цилиндрического конденсатора |
| Относительная диэлектрическая проницаемость |
| Радиус внутренней обкладки |
| Радиус внешней обкладки |
| Длина цилиндрического конденсатора |
| Полученные характеристики цилиндрического конденсатора |
|
Цилиндрический конденсатор представляет в простейшем случае две трубки разного диаметра вложенных друг в друга. разделенных диэлетриком Иногда может получится так, что ёмкость цилиндрического конденсатора станет отрицательной величиной. Ничего страшного, это лишь говорит о том что Вы перепутали радиусы внешней и внутренней оболочки местами. |