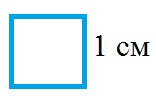Давайте вспомним, как найти площадь прямоугольника. Чтобы найти
площадь прямоугольника, надо длину умножить на ширину.
Вот формула для нахождения площади прямоугольника:
S = a · b
В этой формуле латинской буквой S обозначается площадь, буквами a и b – стороны прямоугольника.
Выполним задание, в котором надо найти площадь
прямоугольника со сторонами 5 см и 3 см.
Решение. Итак, чтобы найти площадь
прямоугольника, надо его длину умножить на ширину.
Произведение чисел 5 и 3 равно 15. Значит, площадь прямоугольника
равна 15 квадратным сантиметрам. Не забудьте, что площадь измеряется именно в
квадратных единицах. В данной задаче это квадратные сантиметры. Также важно
помнить, что длина и ширина должны быть выражены в одинаковых единицах длины.
3 · 5 =
15 (см2)
Ответ: площадь прямоугольника равна 15 см2.
Теперь давайте найдём площадь квадрата со стороной 4 см.
Решение. У этого квадрата каждая
сторона равна 4 см, поэтому умножим 4 на 4 и получится, что площадь квадрата
равна 16 квадратным сантиметрам.
4 · 4 =
16 (см2)
Ответ: площадь квадрата равна 16 см2.
Ну а сейчас перейдём к решению задач, в которых нам надо будет
найти площадь сложных фигур.
Найдите площадь фигуры, изображённой на рисунке.
Эта фигура не является ни прямоугольником, ни квадратом. Но мы
можем разделить эту фигуру на два прямоугольника, например, вот таким образом.
А площади прямоугольников мы легко можем найти с помощью
известной формулы.
Напомним, что противоположные стороны прямоугольника равны.
Итак, стороны первого прямоугольника равны 5 см и 4 см.
5 · 4 =
20 (см2) – площадь первого прямоугольника
Найдём площадь второго прямоугольника.
Ширина этого прямоугольника равна 2 см.
7 – 4 = 3 (см) – длина второго прямоугольника
3 · 2 = 6
(см2) – площадь второго прямоугольника
Мы нашли площади прямоугольников, из которых состоит сложная
фигура. Чтобы найти площадь этой фигуры, надо сложить найденные площади.
20 + 6 = 26
(см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 26 см2.
Площадь этой сложной фигуры найти другим способом. Можно разделить
её на два прямоугольника вот таким образом.
Найдём площадь первого прямоугольника.
Одна его сторона равна 4 см.
5 – 2 = 3 (см) – длина стороны первого прямоугольника
4 · 3 =
12 (см2) – площадь первого прямоугольника
Теперь найдём площадь второго прямоугольника.
7 · 2 =
14 (см2) – площадь второго прямоугольника
12 + 14 =
26 (см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 26 см2.
Решим следующую задачу.
Найдём площадь ещё одной фигуры, изображённой на рисунке.
Чтобы найти площадь этой фигуры, тоже разделим её на простые
фигуры. Сделаем это вот таким образом.
Получилось 3 прямоугольника.
Найдём площадь первого прямоугольника.
7 · 2 =
14 (см2) – площадь первого прямоугольника
Найдём площадь второго прямоугольника.
7 – 4 = 3 (см) – длина одной стороны второго прямоугольника
8 – 2 – 3 = 3 (см) – длина другой стороны второго прямоугольника
Получается, что это квадрат, так как длина всех его сторон равна 3
см.
3 · 3 = 9
(см2) – площадь квадрата
И найдём площадь последнего прямоугольника.
Его ширина равна 3 см. Длина равна 7 см.
3 · 7 =
21 (см2) – площадь третьего прямоугольника
Таким образом, мы нашли площади всех трёх фигур, на которые
разделили данную сложную фигуру. Площадь этой сложной фигуры найдём как сумму
площадей трёх фигур.
14 + 9 + 21 =
44 (см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 44 см2
Отметим, что площадь этой фигуры можно было бы найти, разделив её
на простые фигуры и вот таким образом:
И решим ещё одну задачу.
Найдите площадь незаштрихованной фигуры.
На рисунке изображён прямоугольник со сторонами 9 см и 5 см.
Внутри этого прямоугольника расположен ещё один прямоугольник со сторонами 5 см
и 3 см. Давайте найдём площадь каждого из них.
9 · 5 =
45 (см2) – площадь большего прямоугольника
5 · 3 =
15 (см2) – площадь меньшего прямоугольника
А как найти площадь незаштрихованной фигуры? Площадь этой фигуры
найдём, если из площади большего прямоугольника вычтем площадь меньшего
прямоугольника.
45 – 15 =
30 (см2) – площадь незаштрихованной фигуры
Ответ: площадь незаштрихованной фигуры равна 30 см2.
Содержание:
- § 1 Формула нахождения площади прямоугольника
- § 2 Формула нахождения площади квадрата
§ 1 Формула нахождения площади прямоугольника
В этом уроке рассмотрим такие понятия как площадь фигуры и формулы нахождения площади прямоугольника и квадрата.
Давайте начертим квадрат со стороной 1 см.
Площадь одного такого квадратика называют квадратным сантиметром.
Пишут так:
один сантиметр в квадрате (1 см2).
Соответственно можем сделать вывод, что если какую – либо фигуру можно разбить на несколько таких квадратов, например, р квадратов, то ее площадь равна р см2.
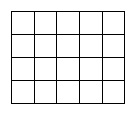
Перед вами рисунок, на котором изображен прямоугольник.
Он состоит из 4 полос, каждая из которых разбита на 5 квадратов со стороной 1 см.
Т.е. весь прямоугольник состоит из 20 квадратов (мы 4 умножили на 5, получили 20).
Значит площадь такого прямоугольника равна 20 см2.
Таким образом, получили правило:
Чтобы найти площадь прямоугольника, надо умножить его длину на ширину.
Это правило можно записать в виде формулы.
Для этого обозначим площадь прямоугольника буквой S, кстати площади всех фигур принято обозначать этой буквой, длину прямоугольника буквой a, ширину – буквой b.
Получаем формулу площади прямоугольника: S равно а умножить на b(S = аb).
§ 2 Формула нахождения площади квадрата
Теперь давайте рассмотрим следующую фигуру – квадрат, это тоже прямоугольник, но у него все стороны равны. Так как квадрат является прямоугольником, то воспользуемся формулой площади прямоугольника (S = аb). Но в случае квадрата b будет равно а, т.е. площадь равна а умножить на а, или принято записывать а в квадрате, значит: (S = а2). Получили еще одну формулу – формулу площади квадрата.
Начертим квадрат со стороной 5 см и найдем его площадь.
Площадь квадрата со стороной 5 см равна 5 в квадрате, т.е. 25 см2.
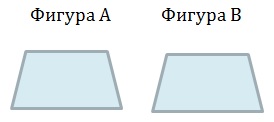
Давайте рассмотрим две фигуры:
Как узнать равны ли эти фигуры?
Это легко проверить, если выполнить наложение, т.е. одну фигуру наложить на другую. Если они полностью совместятся или совпадут, то они равные.
Таким образом, сформулируем правило:
Две фигуры называются равными, если они совпадут при наложении.
А как вы думаете, равны ли их площади и периметры? Конечно, да! Площади равных фигур равны. Периметры равных фигур равны. Но не всегда выполняется наоборот.
Например, прямоугольник со сторонами 16 и 4 см имеет площадь 64 см2 и квадрат со стороной 8 см тоже имеет площадь 64 см2, но эти фигуры не равны между собой.
Давайте построим прямоугольник ABCD со сторонами 7 см и 4 см.
Разделим его на несколько частей.
Первая часть состоит из 8 см2, вторая часть – из 16 см2, третья часть – из 4 см2.
Если сложить все эти части, получим 8 + 16 + 4 = 28. Т.е. сумма площадей всех частей также равна 28 см2.
Итак, можно сделать вывод, что площадь всей фигуры равна сумме площадей ее частей.
Таким образом, на этом уроке мы рассмотрели такие понятия как площадь фигуры и формулы нахождения площади прямоугольника и квадрата.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. — М: 2013.
- Дидактические материалы по математике 5 класс. Автор — Попов М.А. – 2013.
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор — Минаева С.С. – 2014.
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. – 2010.
- Контрольные и самостоятельные работы по математике 5 класс. Авторы — Попов М.А. – 2012.
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений/И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009.
Площади фигур — треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭ
8 класс. Геометрия. Площади фигур. 12.05.2020
ГЕОМЕТРИЯ | Хочешь находить площадь любой фигуры?
Площади геометрических фигур
2016-08-19
При доказательстве теоремы о площадях простейших геометрических фигур параллелограмм преобразуется в прямоугольник, а треугольник и трапеция — в параллелограмм. Знать формулы для площадей этих фигур — хорошо, но понимать, как эти формулы выводятся — гораздо лучше. Что касается формулы для площади круга, здесь надо уяснить пусть и нестрогое, но зато красивое рассуждение с разрезанием круга на большое число секторов и последующим перекладыванием этих секторов в фигуру, близкую по форме к прямоугольнику.
Другие видеоуроки по математика:
Планиметрия
В категории Планиметрия собраны бесплатные онлайн видео уроки по этой теме. Планиметрия (planum, плоскость) — это раздел элементарной (евклидовой) геометрии, в котором изучаются двумерные фигуры, то есть фигуры в пределах одной плоскости. Основными понятиями планиметрии являются точка, прямая, плоскость и расстояние между двумя точками. К основным фигурам, которые изучает планиметрия, относятся: параллелограмм, квадрат, прямоугольник, ромб, трапеция, треугольник, многоугольник и окружность. В планиметрии рассматриваются такие понятия как параллельность прямых, площадь и периметр фигур, подобие и гомотетия, вписанные и описанные многоугольники, аксиомы, теоремы и другие. Изучение планиметрии по видео урокам будет полезно как для начинающих, так и для более опытных математиков. Видеоуроки из рубрики Планиметрия Вы можете смотреть бесплатно в любое удобное время. К некоторым видео урокам по планиметрии приложены дополнительные материалы, которые можно скачать. Приятного Вам обучения!
Как найти площадь треугольника ABC (прямоугольного, с тупым углом, остроугольного), формула
В этом онлайн уроке рассказывается о том, как найти площадь треугольника ABC (прямоугольного, с тупым углом, остроугольного), формула. Начинается обучение с нахождения площади прямоугольного треугольника, т.е. треугольника, в котором один угол равен 90 градусов. Площадь в этом случае вычисляется по очень простой формуле. Она равна половина произведения длин катетов, т.е. двух сторон прилегающих к прямому углу. Справедливость данной формулы объясняется тем, что любой прямоугольный треугольник…
- Математика
- Планиметрия
- Длительность: 11:02
- Рейтинг: 3.9/21
Как найти площадь круга — формула, примеры решения задач
Видео урок «Как найти площадь круга — формула, примеры решения задач» посвящен вопросу о том, как находить площадь круга. Эта задача относится к планиметрии, т.е. изучение фигур на плоскости. Площадь круга — это то, сколько пространства занимает этот круг на поверхности. Для определения площади круга существует специальная формула. Здесь вы узнаете, что собой представляет данная формула и как её использовать при решении задач. В формуле будет использоваться число Пи, т.е. это число, которое…
- Математика
- Планиметрия
- Длительность: 6:49
- Рейтинг: 5.0/1
Теорема Пифагора — формула, решение задач (8 класс)
Это видео посвящено вопросу о том, что такое теорема Пифагора — формула, решение задач (8 класс). Теорема Пифагора является одной из основополагающих теорем математики. Она часто применяется при решении задач в геометрии, и во многих случаях является базисом в тригонометрии. Теорема Пифагора основывается на свойстве прямоугольного треугольника, т.е. треугольника, у которого один из углов равен девяносто градусов. В этом уроке вы узнаете несколько новых терминов, которые относятся к…
- Математика
- Планиметрия
- Длительность: 10:47
- Рейтинг: 3.0/1
Как найти радиус круга, диаметр и длину окружности — формула, решение задач
В этом онлайн уроке рассказывается о том, как найти радиус круга, диаметр и длину окружности — формула, решение задач. По всей видимости, круг является одной из самых главных геометрических фигур нашей вселенной. Достаточно всего лишь посмотреть на форму орбит планет, или то, что можно увидеть на молекулярном уровне. Круг встречается в нашей жизни постоянно. На этом занятии речь пойдет об основных свойствах и параметрах круга. В простом понимании круг представляет собой множество точек…
- Математика
- Планиметрия
- Длительность: 11:00
- Рейтинг: 0.0/0
1
Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.