Описание презентации по отдельным слайдам:
-
1 слайд
Площадь фигур
Турумтаева Р.Ю.
Учитель начальных классов -
2 слайд
ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
-
3 слайд
Работа по учебнику
7
5
Почему получилась разная масса?
Какие единицы массы вы знаете? -
-
5 слайд
Какие единицы длины ты знаешь?
Измерь длину парты в ладонях, в дециметрах. Сделай запись.n= л n= дм
-
6 слайд
Для измерения любой величины надо выбрать мерку — единицу измерения. При разных мерках получаются разные ответы.
Поэтому сравнивать, складывать и вычитать величины можно только тогда, когда они измерены одинаковыми мерками. -
-
-
9 слайд
6
3
2
Вопрос: почему получились разные данные?
Ответ: МЕРКИ разные. -
-
-
-
-
-
15 слайд
учитель начальных классов
Турумтаева Р.Ю.
Урок математики. 2 класс. Автор учебника Л.Г. Петерсон
Тема урока: Площадь фигур
Тип урока: ОНЗ
Цели урока:
— создать условия для формирования представления о величине «площадь», умения сравнивать площади фигур «на глаз», непосредственно и с помощью измерения;
— тренировать способность к сложению и вычитанию трёхзначных чисел.
|
№п/п |
Характеристика деятельности учителя |
Характеристика деятельности обучающихся |
|
1. |
Мотивация к учебной деятельности |
|
|
Звучит песня из м/ф «38 попугаев» «Всё то, что неизвестно» — Как вы думаете, почему именно эта песня прозвучала в начале урока? — А как вы узнаёте новое? — Тогда в добрый путь! |
— Будем узнавать что-то новое, чего раньше не знали. Два шага учебной деятельности: 1. Понять, что не знаю 2. Сам найду способ |
|
|
2. |
Актуализация знаний и фиксация затруднения в пробном действии |
|
|
— С чего начнём работу? — Из какого м/ф прозвучала песня? — Что измеряла мартышка? — Какие мерки она использовала? — В каких мерках длина удава получилась больше? — Почему получилось разное количество мерок? — Что такое длина? — Докажите. — Какие ещё величины знаете? Схема на доске: Величины Длина Масса Объём — Какие способы сравнения величин вы знаете? — О чём нужно помнить при сравнении величин при помощи мерок? — Назовите одним словом фигуры, которые лежат на парте. — Сравните фигуры. Какая из этих фигур занимает больше места на плоскости? Каким способом удобно это сделать? -Наложите прямоугольники друг на друга и сравните, какой из них занимает большее место на плоскости. — Кто может сказать, как называется это свойство фигуры занимать место на плоскости? — Я вам помогу. В математике это свойство фигуры называется ПЛОЩАДЬ. — Что только что делали с площадями фигур? — Можно назвать площадь величиной? — Приходилось в жизни слышать это слово? — Где можно точнее узнать значение слова? — У этого слова несколько значений. Я их озвучу, а вы определите, в каком значении будете использовать это слово на уроке математики. (Определения из словаря Ожегова). — Что повторили? — Почему выполняли именно эти задания? — Что сейчас я предложу вам выполнить? — Попробуйте измерить площадь жёлтого прямоугольника. — Кто не смог выполнить задание? — В чём было ваше затруднение? — Кто смог измерить площадь квадрата? Объясните. |
— С повторения необходимых знаний. — «38 попугаев». — Длину удава. — Мартышка, слон, попугай. — В попугаях. — Мерки разные. — Величина. — Можно измерить, сравнить. — Масса, объём. — «На глаз», наложением, с помощью измерений. — Мерки должны быть равные. — Прямоугольники, четырёхугольники. …….. — «На глаз», наложением, потому что так точнее. — Зелёный прямоугольник. ………? — Сравнивали. — Что называется величиной, знакомые величины, новую величину «площадь», сравнивали площади фигур. — Задание, в котором будет что-то новое. Дети пробуют измерить. ? |
|
|
3. |
Выявление места и причины затруднения |
|
|
— С чем столкнулись? — Что будем делать дальше? — Какое задание не смогли выполнить? |
— Не смогли измерить площадь квадрата. |
|
|
4. |
Построение выхода из затруднения |
|
|
— Какую цель поставите перед собой на уроке? — Вспомните, при помощи чего можно измерить площадь фигуры, если площадь — это величина? |
— Научиться измерять площадь фигуры. — При помощи мерки. |
|
|
5. |
Реализация построенного проекта |
|
|
— Для выполнения задания объединитесь в группы. — Вспомните правила работы в группе. (Каждая группа получает набор мерок а; b; c) — Работать в группах будете по плану: а) измерьте площадь фигуры в мерках а; б) измерьте площадь фигуры в мерках b; в) измерьте площадь фигуры в мерках с — Сравните ваши результаты: К= 6а К= 3b К = 2с — Оцените работу группы. — Почему получилось разное количество мерок? -Понаблюдайте, как изменялось количество мерок, от чего это зависит? — Как измеряли площадь фигур? — Какая должна быть мерка? — Где можно проверить свой вывод? — Сделайте вывод. — Как вы считаете, вы уже хорошо научились измерять площадь фигур? — Что будем делать дальше? |
Объединяются в группы по 4 чел. По ходу работы группы заполняют пропуски: К= …а К= …b К = …с Защита результатов работы групп. Оценивают результаты работы. — Мерки были разные. -Чем больше мерка, тем меньше результат и наоборот. — Выбрали мерку, считали, сколько раз она содержится в фигуре. — Одинаковая. — В учебнике. (Чтение правила в учебнике) — Будем тренироваться. |
|
|
6. |
Первичное закрепление с проговариванием во внешней речи |
|
|
— Прочитайте задание. Что нужно сделать? №4, с.55 учебник — Почему площадь получилась разная? №5, с.56 а) комментирование фронтально; б) работа в парах, проговаривают друг другу — Оцените свою работу в паре. — У кого было затруднение? — В чём? |
— Разные мерки. Проверка по эталону. |
|
|
7. |
Самостоятельная работа с самопроверкой по эталону |
|
|
— Как проверить, что каждый из вас научился измерять площадь фигуры? — Оцените свою работу. — Кто справился? — Кто не справился, в чём ваше затруднение? |
— Выполнить самостоятельную работу. Выполняют с/р и сравнивают результат работы с эталоном. |
|
|
8. |
Рефлексия |
|
|
— Какую цель вы ставили перед собой на уроке? — Удалось вам достичь цели? — Кто смог преодолеть трудности? Что помогло? — Кто не смог? Как вы думаете, почему? — Посмотрите, как вы работали в паре, самостоятельно. Оцените свою работу на уроке. — Какие вопросы остались на конец урока? — Как и где на них можно получить ответ? |
— Научиться измерять площадь фигуры. Самооценка своей работы при помощи «лестницы успеха» |
- Учебники
- 2 класс
- Математика 👍
- Петерсон
- №8
авторы: Петерсон.
издательство: Ювента
Раздел:
- ЧАСТЬ 2
- Урок 42. Комментирование решения уравнения
ГДЗ учебник по математике 2 класс Петерсон. Урок 42. Комментирование решения уравнения. Номер №8
- Предыдущее
- Следующее
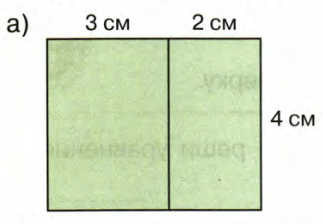
Найди площадь фигур:
reshalka.com
ГДЗ учебник по математике 2 класс Петерсон. Урок 42. Комментирование решения уравнения. Номер №8
Решение а
1) 3 + 2 = 5 (см) − длина фигуры;
2) 5 * 4 = 20
(
с
м
2
)
− площадь фигуры.
Ответ: 20
с
м
2
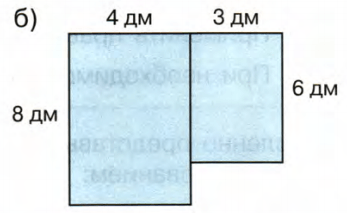
Решение б
1) 4 * 8 = 32
(
д
м
2
)
− площадь большого прямоугольника;
2) 3 * 6 = 18
(
д
м
2
)
− площадь маленького прямоугольника;
3) 32 + 18 = 50
(
д
м
2
)
− площадь фигуры.
Ответ: 50
д
м
2
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Цели урока:
1. Сформировать понятия “площадь” и
“единицы площади”; учить измерять площадь фигур
заданными мерками;
2. Развивать логическое мышление, речь,
память, внимание, математические и
исследовательские способности;
3. Воспитывать умение работать в парах,
группах; прививать любовь к изучению геометрии.
Тип урока: изучение нового материала
(на основе учебной исследовательской
деятельности)
Методы обучения:
репродуктивный (повторение
изученных геометрических фигур, величин и мер их
измерения);
словесный (информационные сообщения
учителя, беседа, стихотворение);
наглядный (работа с таблицами и схемами);
практический (вычерчивание
геометрических фигур на основе программы
действий, измерение площади прямоугольников
разными мерами);
частично-поисковый (исключение “лишних”
мер, определение темы урока);
исследовательский (выбор самой удобной
меры для измерения площади, исследование причин,
по которым из прямоугольников с одинаковым Р
площадь квадрата является наибольшей)
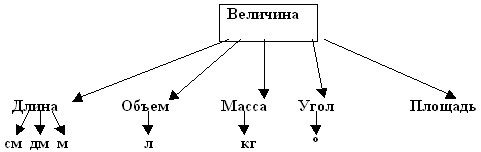
Оборудование: схема “Величина”;
схема “Дерево понятий”; таблица “Программа
действий”; сигнальные квадраты; карточки;
конверты с набором мер разных геометрических
форм; конверты с набором стандартных мер для
измерения площади
Методы стимулирования и мотивации:
– стимулирование интереса к учению
через организацию игры “Путешествие по стране
Геометрии” и самооценку;
– стимулирование долга и ответственности
(убеждение в том, что успех урока-путешествия
зависит от четкой работы каждого)
Методы контроля и самоконтроля:
– устный контроль и самоконтроль
(индивидуальный и фронтальный опрос, в проверке
усвоения правил, рефлексия);
– письменный контроль и самоконтроль
(балльное оценивание самостоятельных и
групповых работ)
Организационно-мотивационный этап
– Сегодня мы продолжаем наше
путешествие по стране Геометрии. А какими
качествами должны обладать путешественники?
(Быть осмотрительными,
внимательными, выносливыми, наблюдательными,
дружными)
– Благодаря этим качествам
путешественники открывают для себя что-то новое.
Я надеюсь, что вы все обладаете данным набором
качеств и сегодня, как настоящие
путешественники, откроете для себя новые знания.
Актуализация опорных знаний
1.Запись даты: 20 декабря.
Характеристика числа (Для записи
этого числа понадобилось 2 цифры, значит оно
двузначное. В нем 2 десятка и 0 единиц. Это число
четное, т.к. у него есть одинаковые части – 10 и 10.
Число 20 круглое, т.к. заканчивается 0. Соседи этого
числа: предшествующее -19, последующее -21.)
2.Построение геометрических фигур
– Каких жителей страны Геометрии вы
знаете? (круг, квадрат, прямоугольник,
треугольник, прямая, угол, луч и т.д.)
– Какие операции мы научились
выполнять с геометрическими фигурами? (чертить,
измерять, сравнивать, находить периметр)
– Что такое периметр? (Сумма длин
всех сторон)
Задание: Надо построить
прямоугольник, периметр которого равен 12см.
(вывесить табличку: Р=12см)
– Определим программу действий.
– С чего начнем? (Дети вспоминают
алгоритм выполнения данного задания. Затем он
вывешивается на доске)
Программа действий:
1.Найти полуР.
2. Найти 2 таких числа, при сложении
которых получится значение полуР. Эти числа и
будут сторонами прямоугольника.
3. Начертить прямоугольник с
полученными сторонами.
– Находим полуР: 12=6+6 (вывесить
табличку) —> полуР = 6 см
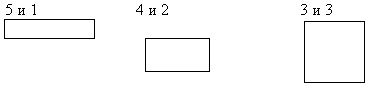
– Вспоминаем состав числа 6: 5 и 1, 4 и 2, 3
и 3. (вывесить таблички)
1-ый ряд чертит прямоугольник со
сторонами 5см и 1см,
2-ой ряд – со сторонами 4 см и 2 см,
3-ий ряд со сторонами 3 см и 3 см.
– Сравните свой прямоугольник с
прямоугольником соседа. (В это время прикрепить
к доске шаблоны прямоугольников)
Рефлексия: – Какие знания
пригодились нам для выполнения этого задания? (1.
Что такое прямоугольник.
2.Что такое периметр.
3. Знание алгоритма построения
прямоугольника по известному периметру.
4. Знание состава чисел 12 и 6.
5. Умение чертить прямоугольники.)
Самооценка: – Поставьте на полях
“5”, если вы поняли, как мы выполнили это задание
и сможете, при необходимости, объяснить его
товарищу.
“4” – если поняли, но объяснить еще
затрудняетесь
Если у вас возникли большие сложности
при выполнении этого задания, то поставьте себе
“-”
– У кого “5”? У кого “4”? У кого “-”?
– Молодцы, путешествуем дальше.
3.Величины
“Знаете ли вы?”
– В группе слов найдите лишнее слово.
Почему оно лишнее? Обсудите в паре.
|
Метр |
— Каким общим
Лишнее слово – килограмм, т.к. все |
|
Килограмм |
|
|
Сантиметр |
|
|
Дециметр |
– Какие еще величины вы знаете?
Заполняется схема:
Самооценка: – Если вы сами нашли
лишнюю величину и вспомнили меры величин, то
поставьте себе на полях “5”.
– Если вы определили лишнюю величину и
вспомнили меры с помощью соседа, то поставьте
“4”.
– А если забыли многие величины и их
меры, поставьте на полях “-”.
– У кого “5”? У кого “4”? У кого “-”?
“Открытие” нового
1.Определение темы урока. Постановка
учебных задач.
– Посмотрите внимательно на
полученную схему и попытайтесь определить тему
урока-путешествия.
(На дерево понятий вывешиваются
таблички со словами “Площадь” и “Единицы (меры)
площади”)
– Поставьте учебные задачи (цели).
(Узнать новое о площади, познакомиться
с мерами площади, научиться измерять площадь)
2.Площадь
Работа в паре. Взаимооценка.
– Что такое площадь? (Величина,
которая указывает, сколько места занимает фигура
на плоскости, называется площадью)
– Расскажите это определение в паре и
оцените друг друга.
– Кому поставили “5”? Кому “4”? Кому
“3”?
– Для чего надо знать определения?
– Давайте вспомним, как измеряются
любые величины?
(Выбирается мерка и устанавливается,
сколько раз она содержится в измеряемой
величине).
– Сейчас вы будете работать в
группах. Послушайте, что надо сделать:
– положить перед собой желтый
прямоугольник (6см х 3см), взять конверт с надписью
“мерки”. В нем вы найдете меры разных
геометрических форм. Ваша задача состоит в том,
чтобы исследовать, какими мерами лучше, удобнее
пользоваться для измерения площади желтого
прямоугольника.
Вывод: Квадрат – самая удобная
единица (мера) площади.
– Квадратами очень удобно замащивать
плоские участки, а скажем кругами такого не
сделаешь без дыр и наложений. Часто математики
вместо слов “нахождение площади” говорят “квадрирование”
(На дерево понятий вывешивается
табличка “квадрирование”)
– Кто понял значение этого слова?
Объясните.
– Измерьте площадь желтого
прямоугольника имеющимися у вас
мерами-квадратами. Сколько квадратных мер у вас
получилось?
(8 кв., 2 кв., 18 кв.)
– Почему так получилось?
(Дети могут предположить, что могут
быть разными измеряемые прямоугольники, или
используемые меры разного размера)
– Как узнать, одинаковые ли по площади
ваши прямоугольники?
(С помощью наложения). Они совпали,
значит, площадь их одинакова.
– Теперь покажите свои мерки-квадраты.
Что вы можете о них сказать?
(Форма одинакова, а размеры разные)
– Можем ли мы теперь ответить на
вопрос, почему у вас получились разные числа при
измерении площади желтого прямоугольника?
(Одинаковые прямоугольники измеряли
разными мерами)
– Какое правило себе напомнили?
(Вспомнили, что сравнивать,
складывать и вычитать величины можно только
тогда, когда они измерены одинаковыми мерками.)
– Как поступить, чтобы при решении
этой задачи у всех детей могли получиться
одинаковые числа?
(Нужно изготовить для всех одинаковые
меры и пользоваться только ими)
– Такая одинаковая (общая) для всех
мера называется стандартной.
(На дерево понятий вывешивается
табличка “стандартная мера”)
– В 1870 и 1872гг. международная
комиссия сначала 24-х, позднее 30 государств
рекомендовала создать в Париже специальное
международное бюро мер и весов, которому
поручается ведать изготовлением и хранением
стандартных мер. Эти меры и сейчас хранятся в
подвале международного бюро мер в Париже.
– У вас на партах лежат конверты с
надписью “стандарт”. В них лежат
стандартные меры для измерения площади. Возьмите
самые маленькие из них и измерьте еще раз площадь
желтого прямоугольника (в конверте лежат мерки 1см2
и 1дм2) .
Как измерить площадь?
Нет задачи проще!
Поглядите-ка сюда:
Стали мерки в три ряда,
Будто бы солдатики –
Ровные квадратики.
Чтобы площадь нам узнать,
Нужно их пересчитать.
– Какое число у вас получилось? (18кв.)
Вывод: При измерении фигур
стандартными мерами получаются одинаковые
числа.
– Возьмите каждый по маленькой мерке.
Измерьте линейкой её длину. Чему равна сторона
квадрата? (1см) Поэтому эту меру называют квадратным
сантиметром.
– Начертите эту меру у себя в тетради.
Сколько клеточек в квадратном сантиметре?
(4клетки). Обозначается эта мера так: 1см?. Запишите
её рядом с начерченным квадратом.
3.Работа в альбомах
– На стр.58 найдите задание №3.Измерьте
площадь каждой фигуры в квадратных сантиметрах и
запишите результат.
(а=8см?, в=11см?, с=12см)?
Самооценка: – Поставьте на полях
“5”, если все подсчеты верны, “4”, если есть одна
ошибка и “-”, если ошибок больше.
– У кого “5”? У кого “4”? У кого “-”?
– Почему быстро удалось измерить
площадь данных фигур? (фигуры уже были поделены
на квадратные сантиметры)
4. Работа в тетрадях
– Измерьте площадь прямоугольников,
начерченных в ваших тетрадях, разбив их на
квадраты со стороной 1см. Проверьте мою работу (перевернуть
прямоугольники обратной стороной, где они
разделены на кв. см).
– Запишите полученные результаты. (5см?,8см?,
9см?)
– Оцените мою работу (под каждым
прямоугольником прикрепить карточки с
результатами площадей). У кого не так?
Самооценка: – Кто правильно разбил
свои прямоугольники на кв. см и правильно
подсчитал их количество, поставьте себе “5”. А у
кого были к себе небольшие замечания поставьте
себе “4”.
– Вспомните, какой Р был у этих
прямоугольников?
(Одинаковый, 12см)
– А что можно сказать о площади этих
прямоугольников? (она разная)
– Почему получились разные площади?
Посоветуйтесь в парах.
(Потому что разные стороны (измерения)
– А в каком прямоугольнике наибольшая
площадь? (у квадрата)
5. Работа в группах.
– Давайте, исследуем, почему площадь
квадрата является наибольшей. Для этого найдите
разницу между длиной и шириной в каждом
прямоугольнике и соотнесите ее с площадью.
Сделайте вывод.
Вывод: Чем меньше разница между
длиной и шириной, тем больше площадь. Если
разница между длиной и шириной равна 0, то это
квадрат. Значит, у квадрата самая большая
площадь.
– Именно по этой причине квадрат и
выбран в качестве стандартной меры площади.
Самооценка: – Если ваша группа
сделала такой же вывод, поставьте на полях “5”,
если вам это не удалось, поставьте пока “-”.
– У кого “5”? У кого “-”?
6. Индивидуальная работа по
разноуровневым карточкам
Ф.И. ученика _________________________________
|
№п/п |
Вид задания |
Задание |
|
1. |
Напиши единицы измерения:
а) длины; б) площади |
а) _______________________________
б) _______________________________ |
|
2. |
Начерти прямоугольник со сторонами 3см и 5см. Найди его площадь. |
|
|
3. |
Сколько квадратов на рисун-ке? А сколько прямоугольни-ков? Запиши их. Измерь пло-щадь самого маленького пря-моугольника. |
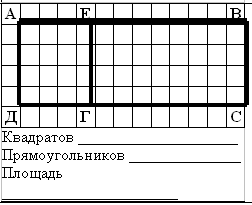 |
– Кто выбрал задания 1-ого уровня?
Почему? Кто 2-ого? Почему? Кто 3-его?
– У кого возникли проблемы? Какие?
Коллективная проверка и самооценка
7. Знакомство с другими мерами площади.
– В конвертах с надписью “стандарт” у
вас осталась еще одна мера. Посмотрите на нее. Кто
догадался, как она называется? (1дм?). Посмотрите
как обозначается эта мера (показать
табличку-образец). Из каких мерочек она
состоит? (кв. см). Сколько их? (100)
Запись: 1дм?= 100см?
– Как вы думаете, для чего
понадобилась ещё одна мера площади?
Посоветуйтесь в паре (для измерения разных по
размеру площадей)
– Есть ещё одна более крупная мера, она
называется кв. метр. Кто знает, как её построить? (начертить
квадрат со стороной 1м)
8. “Мостик” к следующему уроку
– Кто захотел познакомиться поближе с
мерами площади?
– Этим мы займёмся в наших следующих
путешествиях по удивительной стране Геометрии.
Рефлексия
– Удалось ли нам стать настоящими
путешественниками и сделать новые открытия?
– Расскажите о своих открытиях в
парах. А поможет вам в этом “Дерево понятий”.
– Поделитесь теперь своими открытиями
со мной.
Самооценка: – Посмотрите, какие
оценки вы ставили себе на полях. Проведите черту
и поставьте итоговую оценку.
– У кого “5”? У кого “4”? У кого “3”?
– Какая геометрическая фигура была
главной в нашем путешествии? (квадрат)
– Возьмите свои сигнальные квадраты.
Если вам понравилось сегодня путешествовать по
стране Геометрии и открывать новые знания,
покажите мне красные квадраты. А если у вас
такого желания не возникло, покажите синий
квадрат.
– Я с удовольствием сегодня
путешествовала вместе с вами, спасибо!
4. «Открытие» нового знания.
1) Подготовка
— Ещё в далёкие исторические времена человеку приходилось постепенно постигать не только искусство счёта, но и измерений. С развитием науки, техники у людей возникла острая потребность измерять расстояния, объём, массу, время, а затем и площадь. У каждого народа были свои единицы измерения. Например, на Руси в древности для измерения длины пользовались теми мерками, которые всегда были при себе: пальцы, локти, ступни.
— Давайте попробуем измерить ширину парт ладонями (учитель демонстрирует на доске)
— Сколько ладоней составляет ширина парт? (слушает ответы нескольких учеников) Почему получились разные ответы?
— Мы не смогли дать однозначный ответ на вопрос. У нас возникла проблема. Так и в далёкие времена возникали споры. Послушайте задачу: 2 купца мерили длину одинакового отреза ткани локтями. Один отмерил 29 локтей, другой – 30 (Учитель демонстрирует с помощью шарфа, как купцы отмеряли длину отреза ткани, затем вызывает ученика, который повторяет действия учителя и оба называют получившиеся значения)
— Почему получился разный результат?
— К какому выводу пришли люди?
— Со временем люди поняли это, поэтому сейчас во всём мире используют более точные общие для всех стран единицы измерения. Какие линейные единицы измерения дины вы уже знаете?
— Ребята, наши предки научились измерять длину одной из первых и с введением единиц измерения этой величины споров больше не возникало. Тогда наши предки столкнулись с другой проблемой: как измерить площадь земель (крестьянских пашен, земельных наделов). Долго люди не могли понять как же измерить площадь, какие выбрать мерки.
— Но прежде, чем работать дальше, наберёмся сил (проводится физкультминутка)
ФИЗКУЛЬТМИНУТКА
Дружно с вами мы считали и про числа рассуждали.
А теперь мы дружно встали, косточки свои размяли.
На счёт раз кулак сожмём. На счёт два в локтях согнём. На счёт три прижмём к плечам. На четыре – к небесам. Хорошо прогнулись и друг другу улыбнулись. Про 5 не забудем. Добрыми всегда мы будем! На счёт 6 прошу всех сесть.
2) Изучение нового материала
— Посмотрите на доску и назовите фигуры, которые вы на ней видите (у учителя на доске круг, квадрат, прямоугольник, треугольник и пятиугольник).
— Посмотрите, я беру квадрат и провожу рукой по его поверхности. Эту внутреннюю область фигуры называют площадью (таким образом учитель демонстрирует площади всех фигур на доске).
— Ребята, у вас на партах лежат такие же наборы из геометрических фигур. Покажите по очереди друг другу рукой и у доски площади этих фигур.
— Молодцы! А теперь давайте покажем площади различных предметов в окружающей обстановке класса. (Учитель поочерёдно вызывает ребят показать площади поверхности учебника, тетради, доски).
-Ребята! Обратите внимание, что площадь и периметр – это разные величины! Что такое периметр?
А площадь – это внутренняя часть фигуры, ограниченная ломаной линией.
3) Практическая работа.
— Теперь мы знаем, что такое площадь, значит мы можем научиться её измерять. Из вашего набора возьмите самую большую и самую маленькую на ваш взгляд фигуры. И покажите мне. Почему вы так решили?
— Как вы думаете, когда мы говорим о величине фигуры (большая, маленькая), что мы у них сравниваем?
— Верно, площадь характеризует больше или меньше места фигура занимает на плоскости.
— Попробуйте найти одинаковые по площади фигуры. Почему вы так решили?
Учитель предлагает сравнить площади круга и треугольника.
— Какой вывод можно сделать, сравнив площади этих фигур?
Таким же образом учитель предлагает сравнить площади других фигур.
— А теперь посмотрите на доску. Мы видим 2 крестьян, которые спорят, чей же участок земли больше (учитель демонстрирует на интерактивной доске 2 участка прямоугольной формы разного цвета, но одинакового размера, состоящие из разного количества мерок).
— Какой формы эти участки?
— На сколько мерок разбит 1 участок?
— На сколько мерок разбит 2 участок?
Учитель предлагает сравнить площадь фигур по найденному числу мерок и наложением.
— Почему же так получилось?
Очень хорошо! Спор одних мы разрешили, а теперь спорят другие (на интерактивной доске изображение фигур, разбитых на одинаковые по размеру квадраты, по 9 в каждой фигуре, но по-разному расположенных). Можно сравнить площади этих фигур наложением?
— Ребята, попробуйте сделать вывод: если нельзя наложить одну фигуру на другую, то как узнать, какая из них больше или меньше по площади?
— А теперь давайте немного отдохнём и сделаем гимнастику для глаз
Чтобы нам не уставать, надо плюс нарисовать.
Забот у нас не мало – идём за точкой мы по красному овалу.
Зоркость чтоб развить немножко идём за точкой вновь по синей мы дорожке.
Мы на месте не стоим – за точкой по восьмёрке побежим.
— Ребята, для измерения площади фигур нельзя брать какие угодно мерки. Иначе при измерении площади одной и той же фигуры будут получаться разные числа. К такому выводу пришли учёные Ньютон и Лейбниц и решили обозначать площадь буквой S.
Первая мерка, с которой мы подробно будем знакомиться на следующем уроке, называется квадратный сантиметр. (демонстрируется мерка 1 см2)
— Что представляет собой эта мерка?
Обозначается эта мерка см2. Начертите у себя в тетради такую же мерку и обозначьте её. Проверьте друг у друга.
— Что можно измерить с помощью квадратных сантиметров?
Дети слушают, смотрят слайд презентации.
Измеряют ширину парт своими ладонями.
Дети называют ответы. Приходят к выводу, что при измерении получились разные значения, так как длины ладоней у всех разные.
Дети отвечают, что длины локтей у всех разные, поэтому и ответы разные. Приходят к выводу, что для измерения длины нужно пользоваться одинаковыми мерками.
Ребята называют известные им единицы измерения длины.
Дети выполняют движения.
Дети видят наборы геометрических фигур на доске и у себя на парте. Они называют фигуры и показывают их сидя за партами.
Ребята наблюдают за действиями учителя.
Дети по очереди демонстрируют друг другу и у доски пощади фигур, лежащих на парте.
Выходят к доске и показывают площадь предметов, которые называет учитель.
Дети называют определение периметра.
Берут фигуры в руки и демонстрируют учителю.
Называют ответы, приходят к выводу, что определили «на глаз».
Отвечают на вопрос. Делают вывод, что в этом случае мы подразумеваем площадь фигур.
Ребята выбирают одинаковые на их взгляд фигуры. Обосновывают своё решение. Приходят к выводу, что необходимо наложить фигуры друг на друга, чтобы сказать точно, одинаковые фигуры по площади или нет.
Используют способ наложения. Приходят к выводу, что площадь треугольника меньше, так как весь треугольник находится внутри круга.
Ребята делают вывод, что площадь треугольника меньше площади круга или площадь круга больше площади треугольника.
Ребята сравнивают разные фигуры из набора и делают выводы, площадь каких фигур больше или меньше других.
Дети смотрят на доску, отвечают на вопросы учителя.
Ребята делают вывод, что по числу мерок фигуры не равны, а при наложении совпадают.
Приходят к выводу, что нужно мерить одинаковой меркой.
Дети рассуждают и приходят к выводу, что эти фигуры наложить друг на друга нельзя, но раз эти фигуры разбиты на одинаковые квадраты ( мерки), то их нужно посчитать и таким образом сравнить площади участков.
Считают мерки и приходят к выводу, что эти участки разбиты на одинаковое количество мерок, поэтому эти участки равны по площади.
Ребята делают вывод, что если нельзя наложить фигуры одну на другую, то фигуры нужно разбить на одинаковые мерки и эти мерки посчитать и сравнить.
Дети слушают учителя и выполняют упражнения, рисуя глазами называемые фигуры .
Дети отвечают, что это квадрат со стороной 1 см. Чертят в своих тетрадях квадратный сантиметр и обозначают её. Проверяют друг у друга правильность выполнения задания.
Предлагают свои варианты.
Познавательные УУД (личностные и коммуникативные в случае затруднений выполнения задания соседом по парте)
Познавательные УУД, коммуникативные УУД
Познавательные УУД, коммуникативные УУД
Познавательные УУД , регулятивные УУД
Познавательные УУД
Познавательные УУД
Познавательные УУД, регулятивные УУД
Познавательные УУД
Познавательные УУД, регулятивные УУД, коммуникативные УУД, личностные УУД