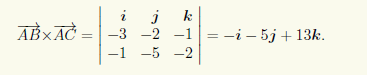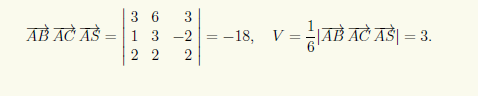Как найти площадь фигуры через координаты - Исправление недочетов и поиск решений вместе с Examum.ru

Площадь по заданным координатам.

Как найти (вычислить) площадь фигуры (треугольник, четырехугольник, трапеция, многоугольник и др.) по координатам?

Какие есть формулы и методы, позволяющие находить площадь через координаты?

бонус за лучший ответ (выдан): 5 кредитов

Для вычисления площади простого многоугольника с любым количеством вершин, представленных в виде списка координат, при последовательном обходе которых, не образуются пересекающиеся линии, применяется формула Гаусса, иначе называемая «формулой землемера», «формулой геодезиста», «формулой шнурования», «алгоритмом шнурования», а так же «методом треугольников».

Суть метода заключается в построении треугольников, состоящих из сторон многоугольника и лучей проведённых из начала координат к вершинам многоугольника, и сложении площадей треугольников, включающих внутреннюю часть многоугольника с вычитанием площадей треугольников, расположенных снаружи.

Площадь, вычисленная по приведенной формуле, будет иметь отрицательное значение при обходе фигуры по часовой стрелке и положительное при обходе против часовой стрелки.

Фигура многоугольника может иметь произвольную геометрию. Например:

Список координат многоугольника представлен в виде массива: (x1, y1), (x2, y2), (x3, y3),…(xn, yn).

Для многоугольника на первом рисунке он задан точками: (3,4), (5,11), (12,8), (9,5), (5,6). Его площадь будет равна:

Существует также метод трапеций, основанный на сложении и вычитании площадей трапеций, образованных каждой из сторон многоугольника, её проекцией на ось абсциссы и перпендикулярами, опущенных из вершин на абсциссу. При обходе вершин по часовой стрелке учитывается величина координаты вершин. Если первая вершина меньше второй, то площадь трапеции прибавляется, если нет, то отнимается.

Для многоугольника ABCDE на левом нижнем рисунке существует 5 трапеций : ABJH, CBJF, CDIF, EDIG и EAHG.

Так как X1<X2, X3<X4 и X5<X1, то площади трапеций ABJH, CDIF и EAHG складываются, а X3>X4 и X4<X5, следовательно, площади трапеций CBJF и EDIG вычитаются:

S = S(ABJH) – S(CBJF) + S(CDIF) – S(EDIG) + S(EAHG)

Площади трапеций рассчитываются по формуле;

Sтрапеции = 1/2 *((a+b))*h,

где a, b – основания трапеции,

h – высота трапеции.

Значения a, b и h вычисляются по координатам.

В декартовых координатах круг может быть представлен двумя точками: центр А и любая точка В, лежащая на окружности. Для расчета площади круга необходимо вычислить его радиус по формуле:

автор вопроса выбрал этот ответ лучшим

Ксарфакс
[156K]

5 лет назад

Площадь фигуры по координатам вершин

Если известны координаты всех вершин, то площадь заданной геометрической фигуры (треугольника, прямоугольника, трапеции, ромба и т.д) можно найти по стандартным формулам. Но предварительно нужно найти длину сторон, диагоналей и т.п. (всё зависит от фигуры) с помощью формулы нахождения длины отрезка по заданным координатам.

Эта формула выглядит следующим образом:

Здесь:

AB — отрезок,

точка A имеет координаты (x1, y1),

точка B имеет координаты (x2, y2).

Рассмотрим несколько примеров.

1) Треугольник ABC имеет координаты A(2,3); B(6,7); C(5,0). Его площадь можно найти по формуле Герона:

Здесь:

S — площадь треугольника,

a, b, c — стороны,

p — полупериметр, который равен половине суммы сторон a, b и c.

Найдём, чему равны стороны треугольника по формуле нахождения длины отрезка по координатам:

AB = √(4² + 4²) = √32 ≈ 5,66.

AC = √(3² + (-3)²) = √18 ≈ 4,24.

BC = √((-1)² + (-7)²) = √50 ≈ 7,07.

Полупериметр треугольника будет равен (5,66 + 4,24 + 7,07) / 2 ≈ 16,97 / 2 ≈ 8,49.

Отсюда площадь треугольника ABC ≈ √(8,49 * 2,83 * 4,25 * 1,42) ≈ √145 ≈ 12,04.

2) Ромб ABCD имеет координаты A(1,2); B(3,4); C(5,2); D(3,0). Площадь можно найти через диагонали:

Здесь:

S — площадь ромба,

d1 и d2 — диагонали.

Таким образом, нам нужно найти диагонали AC и BD.

AC = √(4² + 0) = √16 = 4.

BD = √(0 + (-4)²) = √16 = 4.

Отсюда площадь ромба ABCD = 0,5 * 4 * 4 = 8.

3) Трапеция ABCD имеет координаты A(1,1); B(3,4); C(5,4); D(6,1). Стандартная формула площади трапеции такая:

Здесь:

S — площадь трапеции,

a и b — основания,

h — высота.

Высота трапеции (пусть это будет BE) — это перпендикуляр, который был опущен из вершины трапеции (из точки B) на её основание (в нашем случае это AD).

Определим координаты её отрезка:

координаты первой точки совпадают с точкой B, это (3,4).
координаты 2 точки (точка E) будут (3,1) — так как абсцисса совпадает с абсциссой точки B, а ордината совпадает с ординатой точек A и D.

Высота трапеции BE = √(0 + (-3)²) = √9 = 3.

Теперь посчитаем длину оснований:

BC = √(2² + 0) = √4 = 2.

AD = √(5² + 0) = √25 = 5.

Таким образом, площадь трапеции ABCD = 3 * 0,5 * (2 + 5) = 10,5.

Степан-16
[34.5K]

6 лет назад

Первоначально нужно вычислить длины сторон. В этом здесь будет основная задача. Получив стороны, вычисляем площади по стандартным формулам.

Самый простой случай — для прямоугольника, когда его стороны параллельны осям координат. Тогда одна сторона будет равна разнице абсцисс, вторая ординат.

Треугольник. Допустим, основание параллельно оси абсцисс. Вычисляем его длину, как разницу абсцисс. Далее нужно найти высоту. Она будет равна разнице ординат третьей вершины и ординаты любой из вершин основания. Затем — площадь по формуле: половина произведения основания на высоту.

И т.д.

Если же стороны фигуры не параллельны осям, то находить длины сторон придется уже более сложными расчетами. Допустим, прямоугольник. Первую сторону будем искать, как если бы она была гипотенузой в составе прямоугольного треугольника. Каждая сторона будет равна квадратному корню из суммы квадратов абсцисс и ординат концов отрезков стороны.

Так и для любой фигуры. Вначале определяем длины сторон как гипотенузу треугольника. После чего применяем стандартные формулы площадей.

Эления
[445K]

3 года назад

Рассчитать площадь какой угодно геометрической фигуры, зная координаты, не составляет сложности. Каждая из точек, соответствующая вершинам искомой фигуры, будь это треугольник, четырех- или многоугольник, имеет определенную координату, а значит у нее есть значение, через которое можно рассчитать площадь.

Координаты, как найти на графике, чтобы узнать площадь фигуры? Проецируем на оси абсцисс и ординат прямые, проведя перпендикуляр из каждой точки. Полученные значения будут исходной величиной. Каждая из сторон фигуры — это разница двух точек на горизонтальную и вертикальную оси. Разница между значениями означает длину стороны фигуры. А зная все стороны и их значение, по формуле находим площадь.

Пример 1. Ищем площадь треугольника.

Мы видим два отрезка зеленого цвета AB и BC, которые образуют стороны равнобедренного треугольника, а основание есть отрезок на оси абсцисс AC.

Даны значения: AC основание в промежутке от «-4» до «+4», то есть длина основания равна восьми.

Будет лучше, если посчитать площадь этого треугольника, как сумму из образовавших его двух треугольников, которые являются прямыми, ABO и BOC, совпадающие прямым углом с координатой «0» на графике.

Известна длина каждй из сторон, образующих прямой угол (AO или OC) х = 4 — 0 = 4 и y = 2 — 0 = 2 (BO).

Зная длину двух сторон, образующих прямой угол (AO и BO), находим длину основания (AB или BC). Тогда уже знаем все длины каждой из сторон обоих прямых треугольников. Остается только найти площадь по формуле:

Зная площадь каждого из прямых треугольников, умножаем на два, получаем сумму заштрихованного треугольника на графике ABC.

И еще математически можно записать решение следующим образом, исходя из того, что имеем изначально следующую систему неравенств:

Пример 2.

Пример 3. Есть парабола, ищем площадь фигуры, ограниченную кривой параболы. Чтобы посчитать, используем интеграл.

Бекки Шарп
[71.2K]

3 года назад

Рассмотрим простой случай, где буквально на пальцах можно посчитать площадь через обычную формулу, а затем применим к этой задаче формулу Гаусса.

У нас есть трапеция, у которой известны координаты вершин. (3:2) (5:2) (9:6) (6:6). Мы знаем, что площадь трапеции равна сумме оснований, деленной на 2 и умноженной на высоту.

S = (a+b)/2 х h Считаем площадь: S = (3+2):2х4 = 10. Ответ — 10.

А теперь по теореме Гаусса.

Не смотря на страшный вид, формула очень простая. В квадратных скобках мы перемножаем абсциссу первой точки с ординатой второй, прибавляем абсциссу второй, умноженную на ординату третьей и так идем по кругу фигуры. Далее вычитаем ординату первой умноженную на абсциссу второй и т.д. В квадратных скобках у нас может получиться отрицательное число.

S= 0,5 х [3х6+6х6+9х2+5х2 — 2х6-6х9-6х5-2х3] = 10

Таким образом можно найти площадь любой сложной фигуры, зная ее координаты.

dydySacha
[10.8K]

6 лет назад

Можно взять милиметровку и нанести точки с заданными координатами, согласно осей абсцис и ординат. Соединить эти точки между собой и замерить длины образовавшихся сторон, а с помощью формулы по определению площади образовавшейся фигуры узнать её значение подставив данные в эту формулу.

Алиса в Стране
[364K]

3 года назад

Существует специальная формула, называемая формулой Гаусса, она и позволит нам определить искомую площадь по координатам. Вот как эта формула выглядит:

Формула выглядит немного устрашающе, но давайте попробуем в ней разобраться. У нас есть многоугольник и есть его координаты, подсчитать n — количество сторон многоугольника несложно, а дальше просто нужно подставлять значения в эту формулу, нужно только быть внимательным и не перепутать какие координаты куда надо писать.

Давайте теперь приведем пример нахождения такой площади через формулу Гаусса. Допустим, у нас есть вот такой пятиугольник:

Координаты его пяти вершин, как мы видим: (3, 4), (5, 11), (12, 8), (9, 5), (5, 6).

Теперь нам остается только очень внимательно подставить эти координаты в нашу формулу, n = 5, координаты известны, вот что у нас получится:

Когда разбираешься в этой формуле, понимаешь, насколько она проста и даже легко запоминается, несмотря на то, что сначала кажется очень сложной.

duselldorf
[4.3K]

5 лет назад

Для вычисления площади геометрической фигуры по координатам ее вершин, нужно воспользоваться формулой Гаусса, иногда ее называют формулой землемера или формулой геодезиста, так как она применяется геодезистами для определения площади земельного участка, например, при межевании:

где

А — площадь многоугольника с заданными координатам его вершин,

n — количество сторон многоугольника,

(xi, yi) — координаты вершин многоугольника,

i = 1, 2,…, n — номер вершины многоугольника.

Бархатные лапки
[382K]

3 года назад

Находим площадь вот такого несложного четырехугольника. Координаты его вершин нам известны. Применяем формулу Гаусса, которая выглядит так:

S (площадь) = 0,5 [6х4 +9х7 + 10х6 + 7х3 — 3х9 — 4х10 — 7х7 — 6х6] = 8 (квадратных единиц)

Как видим если применять при решении формулу Гаусса то решить такую задачку несложно.

Не вижу здесь серьезных проблем. Мы, как я понял, имеем готовые точки координат, которые нужно проставить на координатной плоскости. Далее, соединяя эти точки, получаем фигуру, как в примере вопроса — квадрат, треугольник и т.п.

Теперь вычисляем площадь любой из полученных фигур по формуле ей соответствующей.

Знаете ответ?

Источник

Вычисление площадей фигур в различных системах координат

Площадь плоской фигуры в декартовых координатах

Напомним, что мы назвали криволинейной трапецией фигуру, ограниченную осью абсцисс, прямыми x=a и x=b и графиком функции y=f(x) . В этом пункте выведем формулу для вычисления площади криволинейной трапеции.

Теорема 3. Если функция y=f(x) неотрицательна на отрезке [a;b] и непрерывна на нем, то соответствующая ей криволинейная трапеция квадрируема, причем ее площадь выражается формулой

${ S= intlimits_{a}^{b} f(x),dx,.}$

(4)

Доказательство. Криволинейная трапеция ограничена тремя отрезками и графиком непрерывной функции y=f(x) . Как было показано в пункте 2 такая фигура квадрируема. Чтобы вычислить площадь этой трапеции, построим для нее внешние и внутренние ступенчатые фигуры (см. рис. 26).

Тогда, с одной стороны, имеем:

$sum_{k=0}^{n-1}m_kDelta x_kleqslant Sleqslant sum_{k=0}^{n-1} M_kDelta x_k,,$

где $sum_{k=0}^{n-1}m_kDelta x_k$ — площадь внутренней ступенчатой фигуры, $sum_{k=0}^{n-1}M_kDelta x_k$ —площадь внешней ступенчатой фигуры, $m_k=min_{xin [x_k;x_{k+1}]}f(x)$ и $M_k=max_{xin[x_k;x_{k+1}]}f(x)$ . С другой стороны, по определению интеграла можно записать:

$sum_{k=0}^{n-1}m_kDelta x_kleqslant intlimits_{a}^{b} f(x),dxleqslant sum_{k=0}^{n-1}M_kDelta x_k,.$

Таким образом, числа и $intlimits_{a}^{b} f(x),dx$ разделяют одни и те же числовые множества: $Biggl{,sum_{k=0}^{n-1}m_kDelta x_k,Biggr},$ $Biggl{,sum_{k=0}^{n-1}M_kDelta x_k,Biggr}$ . Но, как было показано при изучении определенного интеграла, эти множества разделяются лишь одним числом, и потому $S=intlimits_{a}^{b} f(x),dx$ . Теорема доказана.

Аналогично доказывается, что если фигура ограничена снизу графиком функции y=f_1(x) , сверху графиком функции y=f_2(x) , а слева и справа прямыми x=a,~x=b (рис. 30), то ее площадь выражается формулой

$S= intlimits_{a}^{b}bigl[f_2(x)-f_1(x)bigr]dx,.$

Наглядный смысл формулы (4) состоит в том, что криволинейную трапецию можно рассматривать как объединение «бесконечно тонких полосок» с основаниями и высотами f(x) .

Площадь фигуры между двумя графиками функций

Пусть теперь функция y=f(x) непрерывна на отрезке [a;b] и принимает на нем только неположительные значения. Выразим с помощью определенного интеграла площадь соответствующей криволинейной трапеции .

Рассмотрим фигуру Phi , симметричную фигуре относительно оси . Эта фигура (рис. 31) представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке [a;b] функции y=f(x) , которая на [a;b] принимает только неотрицательные значения. По доказанному выше

Интегрирование знакопеременной функции

$S(Phi)= intlimits_{a}^{b} bigl(-f(x)bigr)dx$ . Но S(Phi)=S(F).

Значит,

$S(F)= intlimits_{a}^{b} bigl(-f(x)bigr)dx= -intlimits_{a}^{b} f(x),dx,.$

Как мы видим, в рассматриваемом случае интеграл $intlimits_{a}^{b} f(x),dx$ дает значение площади криволинейной трапеции с точностью до знака. Если же функция меняет знак на отрезке [a;b] в конечном числе точек, то значение интеграла $intlimits_{a}^{b} f(x),dx$ дает алгебраическую сумму площадей соответствующих криволинейных трапеций, ограниченных частями графика функции y=f(x) , отрезками оси и, быть может, отрезками, параллельными оси (рис. 32).

Пример 1. Найти площадь фигуры, ограниченной кривой y=e^x , осью абсцисс и прямыми x=1,~x=2 (рис. 33).

Решение. Имеем: $S= intlimits_{1}^{2} e^x,dx= Bigl.{e^x}Bigr|_{1}^{2}= e^2-e= e(e-1)$ (кв. ед.).

Пример 2. Вычислить площадь фигуры, ограниченной дугой параболы y^2=4x и отрезком прямой x=2 (рис. 34).

Решение. Из рисунка видно, что трапеция, площадь которой нужно найти, расположена симметрично относительно оси абсцисс и, следовательно, искомая площадь равна

$S= 2int_{0}^{2}2sqrt{x},dx= left.{frac{4x^{3/2}}{3/2}}right|_{0}^{2}= frac{8}{3}cdot 2^{3/2}= frac{16}{3}sqrt{2},.$

Пример 3. Найти площадь фигуры, ограниченной графиками функций y^2=9x,~ y=3x (рис. 35).

Решение. Искомая площадь равна разности площадей криволинейного треугольника OAB и прямоугольного треугольника OAB:

$S= intlimits_{0}^{1} sqrt{9x},dx- intlimits_{0}^{1} 3x,dx= left.{3cdot frac{x^{3/2}}{3/2}}right|_{0}^{1}- left.{3cdot frac{x^2}{2} }right|_{0}^{1}= 2-frac{3}{2}= frac{1}{2},.$

Площадь фигуры, ограниченной кривой, осью абсцисс и двумя прямыми

Пример 4. Вычислить площадь фигуры, ограниченной петлей кривой a(y^2-x^2)+x^3=0 .

Решение. Из уравнения кривой видно, что она расположена симметрично относительно оси . Следовательно, можно сначала вычислить половину искомой площади (рис. 36). Рекомендуем читателю подробно исследовать и построить данную кривую.

Площадь фигуры, ограниченной петлёй кривой

Записав уравнение кривой в виде $y^2=frac{x^2}{a}(a-x)$ , найдем точки пересечения ее с осью , положив y=0colon, x_1=0,~ x_2=a . Учитывая сказанное, найдем площадь половины петли:

$frac{1}{2}S= frac{1}{sqrt{a}} intlimits_{0}^{a} xsqrt{a-x},dx,.$

Воспользовавшись формулой из таблицы при a=-1,~ b=a , получим:

$intlimits_{0}^{a} xsqrt{a-x},dx= left.{frac{2(-3x-2a)sqrt{(a-x)^3}}{15}}right|_{0}^{a}= frac{4}{15},a^{5/2},.$

Значит, окончательно имеем:

$frac{1}{2}S= frac{1}{sqrt{a}}cdot frac{4}{15},a^{5/2}= frac{4}{15},a^2quad Leftrightarrowquad S=frac{8}{15},a^2,.$

Площадь фигуры, ограниченной кривой, заданной параметрически

Пусть кривая y=f(x),~ f(x)geqslant0,~ aleqslant xleqslant b задана в параметрической форме

$begin{cases}x=varphi(t),\ y=psi(t),end{cases} alpha leqslant tleqslant b,,$

где функция x=varphi(t) монотонна на отрезке [alpha;beta] , причем varphi(alpha)=a, varphi(beta)=b , и имеет на этом отрезке непрерывную производную. Так как y=f(x)= fbigl(varphi(t)bigr)= psi(t) , то по формуле замены переменной под знаком определенного интеграла получаем:

$S= intlimits_{a}^{b} f(x),dx= intlimits_{alpha}^{beta} fbigl(varphi(t)bigr) varphi'(t),dt= intlimits_{alpha}^{beta} psi(t) varphi'(t),dt,.$

Итак, площадь фигуры, ограниченной кривой, заданной параметрически, вычисляется по формуле:

$S= intlimits_{alpha}^{beta} psi(t)varphi'(t),dt,.$

(5)

Пример 5. Вычислить площадь эллипса, заданного параметрически $begin{cases} x=acos{t},,\ y=bsin{t},,end{cases} 0leqslant tleqslant 2pi,.$

Площадь фигуры, ограниченной эллипсом

Решение. Выберем ту часть эллипса (рис. 37), которая расположена в первом квадранте. Точке A(a;0) соответствует значение t=0 , а точке B(0;b) — значение $t=frac{pi}{2}$ . Поэтому

$begin{aligned} S&= 4intlimits_{0}^{a}y,dx= -4intlimits_{0}^{pi/2}bsin{t}cdot(-asin{t}),dt= 4abintlimits_{0}^{pi/2} sin^2t,dt=\ &= 2abintlimits_{0}^{pi/2} bigl(1-cos2tbigr),dt= left.{2ab!left(t- frac{1}{2}sin2t right)}right|_{0}^{pi/2}= pi,ab,. end{aligned}$

Площадь фигуры, заданной в полярных координатах

Вычислить площадь сектора, ограниченного лучами ell и , выходящими из точки , и непрерывной кривой Gamma (рис. 38). Выберем полярную систему координат, полюсом которой является точка . Пусть rho=rho(varphi) — полярное уравнение кривой Gamma , а varphi_0 и Phi — углы между полярной осью и лучами ell и соответственно. При этом пусть функция непрерывна на [varphi_0;Phi] .

Разобьем данный сектор на частей лучами

$varphi_0< varphi_1< varphi_2< ldots< varphi_k< varphi_{k+1}< ldots< varphi_n= Phi$

и рассмотрим k-й частичный сектор $[varphi_k; varphi_{k+1}]$ (рис. 39). Пусть r_k — наименьшее значение функции rho(varphi) в $[varphi_k; varphi_{k+1}]$ , a R_k — наибольшее значение функции в этом отрезке.

Площадь в полярных координатах и разбиение сектора на n частей

Построим два круговых сектора с радиусами r_k и R_k . Обозначим через Deltavarphi_k величину угла рассматриваемого частичного сектора. Тогда площадь частичного криволинейного сектора будет заключена между площадями вписанного и описанного частичных круговых секторов

$frac{1}{2}cdot r_k^2cdot Deltavarphi_k leqslant S_kleqslant frac{1}{2}cdot R_k^2cdot Deltavarphi_k,.$

Построим аналогичным образом внутренние и внешние круговые секторы для всех частичных криволинейных секторов. Объединяя их, получим внутреннюю и внешнюю фигуры.

Площадь внутренней фигуры, состоящей из круговых секторов, равна $frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_k$ , а площадь внешней фигуры равна — $frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k$ . Эти выражения являются нижней и верхней суммами Дарбу s_P и S_P для интеграла $frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi$ . Так как функция rho(varphi) непрерывна, то непрерывна, а потому и интегрируема функция . Поэтому для любого varepsilon найдется такое разбиение отрезка [varphi_0,Phi] , что S_P-s_P<varepsilon . Из теоремы 2 пункта 2 следует, что заданный криволинейный сектор квадрируем. При этом для его площади выполняются неравенства

Площадь, ограниченная одним лепестком полярной розы

$frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_kleqslant Sleqslant frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k,.$

(6)

В то же время по определению определенного интеграла

$frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_kleqslant frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi leqslant frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k,.$

(7)

В силу единственности разделяющего числа из неравенств (6) и (7) следует, что

$S= frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi,.$

(8)

Пример 6. Вычислить площадь, ограниченную одним лепестком розы rho=asin2varphi (рис. 40).

Решение. Значениям varphi=0 и $varphi=frac{pi}{2}$ соответствует rho=0 Поэтому

$S= frac{1}{2} intlimits_{0}^{pi/2} a^2sin^22varphi,dvarphi= frac{a^2}{2} intlimits_{0}^{pi/2} frac{1-cos4varphi}{2},dvarphi= left.{frac{a^2}{4}! left(varphi- frac{1}{4}sin4varphiright)}right|_{0}^{pi/2}= frac{a^2}{4}cdot frac{pi}{2}= frac{pi}{2},a^2,.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Площади многоугольников на координатной сетке

5 февраля 2011

Многоугольники на координатной сетке — это самые простые задачи B5. Существует сразу несколько методов решения таких задачи, в том числе универсальный, описанный ниже. Для начала определимся с терминологией:

Многоугольник — фигура на плоскости, ограниченная замкнутой ломаной.

Большинство многоугольников, встречающихся в ЕГЭ, являются выпуклыми, т.е. не имеют внутренних углов размером больше 180°, а все вершины многоугольника лежат в узлах координатной сетки. Кроме того, ломаная, ограничивающая многоугольник, не имеет самопересечений. Все это значительно упрощает задачу.

Для решения всех задач этого типа достаточно выполнить четыре простых шага:

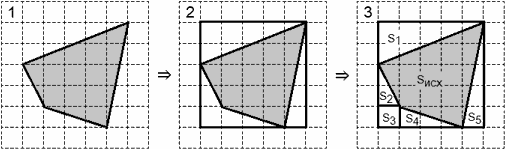
Описать вокруг многоугольника прямоугольник, стороны которого параллельны осям координат (линиям сетки). При этом желательно, чтобы на каждой стороне прямоугольника присутствовала хотя бы одна вершина исходной фигуры;
Разбить внутреннее пространство прямоугольника, не занятое исходной фигурой, на квадраты и треугольники. Лучше, если все линии разбиения будут параллельны осям координат;
Найти площадь каждого элемента разбиения. Сложив эти площади, получим площадь всего разбиения;
Наконец, из площади прямоугольника вычесть площадь разбиения — это и будет площадью исходной фигуры.

Несмотря на большое количество элементов разбиения, вычисление его площади — достаточно тривиальная задача.

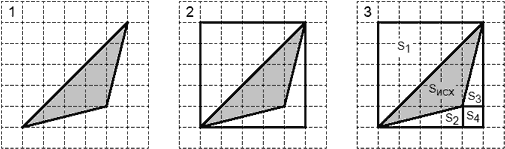
Проиллюстрируем каждый шаг решения:

Последним шагом найдем площадь исходной фигуры: S_исх = S − (S₁ + S₂ + S₃ + S₄ + S₅), где S — площадь описанного прямоугольника. Осталось вычислить площадь большого прямоугольника и элементов разбиения. Эти несложные расчеты предлагается выполнить читателю в качестве упражнения.

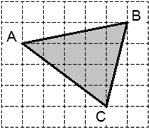
Задача. Найти площадь треугольника ABC, изображенного на рисунке:

Обозначение треугольника можно опустить, поскольку оно нам не потребуется. Приведем первые три шага:

Итак, S_исх = S − (S₁ + S₂ + S₃), где S — площадь описанного прямоугольника. Найдем площадь элементов разбиения:

S₁ = ½ · 1 · 5 = 2,5; S₂ = ½ · 3 · 4 = 6; S₃ = ½ · 1 · 4 = 2; S = 5 · 4 = 20.

Наконец, найдем площадь треугольника: S_исх = 20 − (2,5 + 6 + 2) = 9,5.

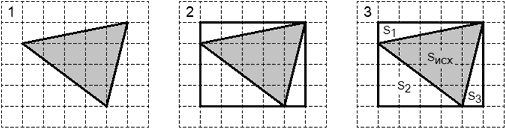
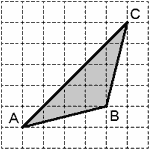
Задача. Найти площадь треугольника ABC, изображенного на рисунке:

Снова выполняем первые три шага. Заметим, что угол ABC — тупой, поэтому в разбиении присутствует квадрат. Имеем:

Очевидно, S_исх = S − (S₁ + S₂ + S₃ + S₄), где S — площадь описанного прямоугольника. Найдем площадь элементов разбиения:

S₁ = ½ · 5 · 5 = 12,5; S₂ = ½ · 4 · 1 = 2; S₃ = ½ · 1 · 4 = 2; S₄ = 1 · 1 = 1; S = 5 · 5 = 25.

Площадь треугольника: S_исх = 25 − (12,5 + 2 + 2 + 1) = 7,5.

Смотрите также:

Задача B5: вычисление площади методом обводки
Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
Системы линейных уравнений: основные понятия
Тест к уроку «Знаки тригонометрических функций» (1 вариант)
Координаты вершин правильного тетраэдра
Задача B2 про комиссию в терминале

Источник

Вычисление площадей многоугольников и объемов многогранников, заданных координатами своих вершин в прямоугольной системе координат, основывается на использовании скалярного, векторного и смешанного произведений векторов.

Если параллелограмм задан в пространстве координатами своих вершин, то для вычисления его площади нужно найти координаты двух векторов, соответствующих смежным сторонам параллелограмма, а затем модуль их векторного произведения. Аналогично вычисляется площадь треугольника, равная половине модуля векторного произведения векторов, на которых он построен как на смежных сторонах.

Пример 4.2. Пусть три вершины треугольника заданы своими координатами: A(4;4;4), B(1; 2; 3), C(3; —1;2).

Для определения площади ΔABC с помощью (4.10) найдем координаты векторов AB и AC: AB = {1 — 4; 2 — 4; 3 — 4} = { — 3; —2; —1}, —1 = {3 — 4; —1 — 4; 2 — 4} = { — 1; —5; —2}.

Затем по (3.2) вычислим их векторное произведение:

Модуль этого векторного произведения равен |AB×AC| = √((—1)² + (—5)² + 13²) = √195, и следовательно, S ΔABC = |AB×AC|/2 = √195/2 #

Для вычисления объема параллелепипеда, заданного координатами своих вершин, нужно найти координаты трех векторов, соответствующих смежным ребрам, а затем вычислить модуль смешанного произведения этих векторов. Через смешанное произведение вычисляется и объем произвольной треугольной пирамиды SABC (см. пример 3.2), поскольку он равен 1/6 объема параллелепипеда, построенного на ребрах AB, AC и AS. Таким образом, объем этой пирамиды равен VSABC = |ABACAS|/6.

Пример 4.3. Найдем объем V пирамиды SABC, заданной координатами своих вершин: A(2; —1;1), B(5; 5; 4), C(3; 2; —1), S(4;1;3).

Используя (4.10), вычисляем координаты векторов, направленных по ребрам пирамиды: AB = {5 — 2; 5 — (—1);4 — 1} = {3; 6; 3}, AC = {3 — 2; 2 — (—1); —1 — 1} = {1;3; —2},= AS {4 — 2;1 — (—1); 3 — 1} = {2;2;2}, и определяем объем с помощью смешанного произведения найденных векторов:

Источник

Самый простой многоугольник и вектор

Чтобы найти площадь треугольника через векторы и известные координаты его вершин, необходимо подробнее познакомиться с этими геометрическими объектами. Знание их свойств позволяет легко вычислять разные характеристики изучаемой фигуры, включая периметр, высоту, углы при вершинах и другие. При этом используются универсальные математические операции, которые можно применять с успехом не только для треугольника, но и для других многоугольников.

Фигура на плоскости

Треугольник в геометрии представляет собой самый простой многоугольник, который лежит всегда в одной плоскости, даже если фигура рассматривается в трехмерном пространстве. Состоит он из сторон и вершины.

Сторон и вершин у фигуры по три. Сторона является отрезком, а вершина — это точка пересечения этих отрезков. Для нее характерен определенный угол. Все углы треугольника являются разными в общем случае, их сумма всегда соответствует 180°. Однако, существуют специальные типы фигуры, для которых либо два угла равны друг другу (равнобедренный), либо все три (равносторонний). В задачах называют треугольники по имени их трех вершин, обозначенных латинскими буквами, например, ABC или NPQ.

Для треугольника важное значение имеют следующие отрезки:

делящий противоположную углу сторону пополам — медиана;
разделяющий угол при вершине на два равных — биссектриса;
падающий под прямым углом на противоположную углу сторону — высота.

Высота, например, используется для расчета площади фигуры. Для равностороннего треугольника все эти отрезки совпадают друг с другом для любой вершины, а для равнобедренного они одинаковы лишь для угла, образованного равными сторонами.

Направленный отрезок

Вектором называют линейный элемент, который имеет начало и конец. Для его определения удобнее всего использовать координатную плоскость. Она представляет собой две направленные оси, имеющие шкалу и пересекающиеся под углом 90°. Точка пересечения является началом координат и обозначается буквой O (0; 0). Здесь каждая из цифр указывает точку пересечение перпендикуляра, опущенного из рассматриваемого объекта к каждой из двух осей.

Если начало A (x0; y0) и конец B (x1; y1) вектора известны, тогда легко можно вычислить его собственные координаты. Делается это так:

AB- = B-A = (x1-x0; y1-y0).

Иными словами, чтобы получить вектор AB-, следует из соответствующих координат его конца вычесть его начало. Эта операция эквивалентна параллельному перемещению AB- в начало координатной плоскости, что говорит о существовании бесконечного количества одинаковых AB-векторов.

Направленные отрезки можно складывать, вычитать и умножать. Для каждой из операций существуют определенные правила. Если для сложения и вычитания речь идет о геометрических особенностях, то в случае умножения применяются исключительно алгебраические выражения. Вектор a- можно умножить на b- двумя принципиально разными способами:

Скалярно: (a-*b-). В этом случае мы получаем число. Правило умножения записывается следующим образом: (a-*b-) = |a-|*|b-|*cos (ab)=x1*x2+y1*y2. Здесь знаком модуля (||) обозначены длины соответствующих отрезков, cos (ab) — это косинус угла между a- и b-, при этом a-(x1; y1), b-(x2; y2). Этот тип произведения можно использовать для вычисления углов между направленными отрезками, а также для определения объема фигур в пространстве.
Векторно: [a-*b-]. Результатом этой операции является вектор, который перпендикулярен исходным, его направление (вверх или вниз) принято определять по правилу правой руки: четыре пальца должны быть направлены от конца a- к концу b-, тогда оттопыренный большой палец укажет направление их векторного произведения. Длина этого перпендикулярного вектора определяется так: [a-*b-] = |a-|*|b-|*sin (ab) = x1*y2-x2*y1. Векторное произведение используют для вычисления площадей фигур.

Методы вычисления площади по координатам

Задачи на вычисление площадей, периметров или объемов фигур по известным координатам их вершин являются типичными для школьного курса геометрии. В связи с развитием современных технологий школьники часто ищут в интернете, как решить треугольник онлайн по координатам. Тем не менее, существует ряд простых способов, которые позволяют быстро найти площадь фигуры, если известно расположение трех его вершин на координатной плоскости.

Универсальный подход

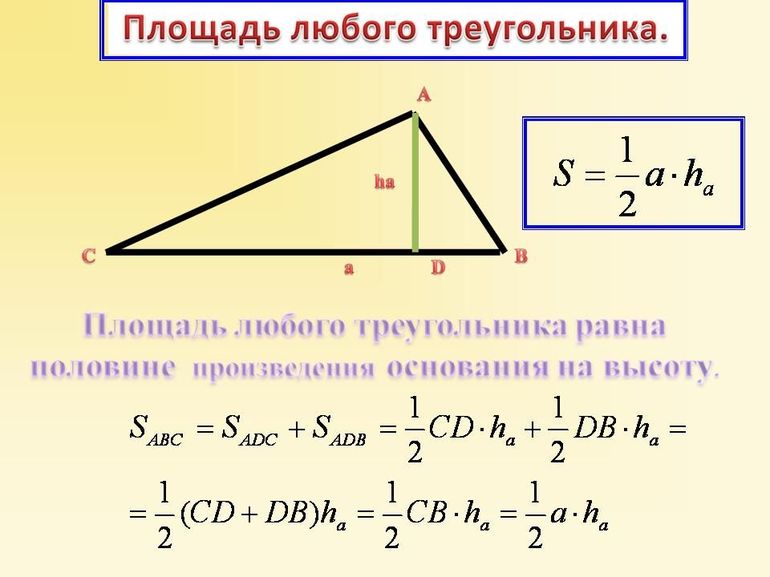
Этот метод можно применять всегда, независимо от того, какой тип треугольника рассматривается. Известно, что площадь фигуры вычисляется, как произведение половины стороны на опущенную на нее высоту: S = ½*a*h.

Пусть имеются координаты вершин заданного треугольника ABC:

A (x1; y1);
B (x2; y2);
C (x3; y3).

Тогда координаты его векторов AB- и AC- выразятся так:

AB- = (x2-x1; y2-y1);
AC- = (x3-x1; y3-y1).

Если провести высоту h треугольника ABC к любой из этих сторон, например, к AC, то ее длина может быть рассчитана с использованием тригонометрической функции синуса:

h = AB*sin (α).

Здесь α является углом между векторами-сторонами AB- и AC-. Тогда формулу площади можно переписать в следующем виде: S = ½*a*h = ½*AC* AB*sin (α).

Можно заметить, что записанное выражение является не чем иным, как векторным произведением для AB- и AC-, поэтому можно переписать формулу для S так:

S = ½*[ AB-* AC- ] = ½*((x2-x1)*(y3-y1) — (y2-y1)*(x3-x1)).

Можно аналогично показать, что подобные выражения получаются для пар векторов AC-, BC- и AB-, BC-.

Рекомендуется не запоминать конечные выражения для площади треугольника, поскольку они являются несколько громоздкими, и при их использовании ученики могут запутаться. Для решения подобного рода задач достаточно понять свойства векторов и единственную универсальную формулу для S для любого типа треугольников.

Любопытно отметить, что векторное произведение при вычислении площади можно применять не только для треугольников, но и для любых четырехугольников. Так, в случае параллелограмма рассматриваемая характеристика будет точно равна векторному произведению любых смежных (непараллельных) его сторон.

Использование формулы Герона

Этот способ также может считаться универсальным, поскольку он применим к любым типам треугольников. В работе Герона Александрийского, которая называется «Метрика» и относится к I веку нашей эры, впервые было обнаружено выражение, позволяющее по длинам сторон рассматриваемой фигуры определить ее площадь. Формула имеет следующий вид:

S = (p*(p-a)*(p-b)*(p-c))^0,5.

Здесь p — полупериметр, a, b, c — длины сторон.

Последовательность этапов решения задачи можно выразить таким образом:

Необходимо определить координаты векторов, образующих стороны треугольника.
Затем, следует вычислить длины их сторон.
Посчитать полупериметр фигуры.
Применить формулу Герона.

Ключевым этапом является определение длины вектора. Пусть AB- имеет координаты (x1; y1), тогда его длина вычисляется так:

|AB-| = (x1² + y1²)^0,5.

Длина любого вектора как на плоскости, так и в пространстве, вычисляется, как сумма квадратов всех его координат, взятых под корень.

Очевидно, что можно записать общее выражение для площади треугольника через координаты с использованием формулы Герона, но оно будет слишком громоздким, поэтому нет никакого смысла запоминать его.

Другие способы

Существуют эмпирические правила, которые можно запомнить и легко решать задачи на определение площади треугольника. Пусть координаты его вершин задаются так: A (x1; y1), B (x2; y2), C (x3; y3). Предположим, что порядок вершин A, B, C расположен против часовой стрелки, тогда существуют следующие правила определения площади ABC:

Можно воспользоваться формулой: S = ½*(x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)). То есть выбирается первая координата вершины и умножается на разность вторых координат двух других вершин, возникающих против хода стрелки часов от первой. Затем, все три члена складываются и делятся на 2.
Матричный способ. Необходимо выписать в столбик пары координат каждой вершины против часовой стрелки и завершить координатами исходной. После этого следует сложить три попарных произведения первой и второй координат двух соседних вершин, а затем, вычесть три попарных произведений второй и первой координат тех же вершин. Результат поделить пополам. Например: (x1; y1) (x2; y2) (x3; y3) (x1; y1). S = ½*(x1*y2 + x2*y3 + x3*y1 — y1*x2 — y2*x3 — y3*x1).

Решение задачи

Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).

Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:

AB- = (2−1; 5-(-3)) = (1; 8);
BC- = (-2−2; -2−5) = (-4; -7).

Чтобы рассчитать площадь, достаточно вычислить полупроизведение векторное для выбранных направленных отрезков: S = ½*[AB-*BC-] = ½*(1*(-7)-8*(-4)) = 12,5 квадратных единиц.

Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.

Источник