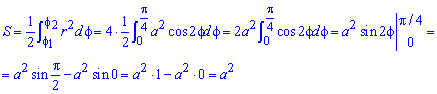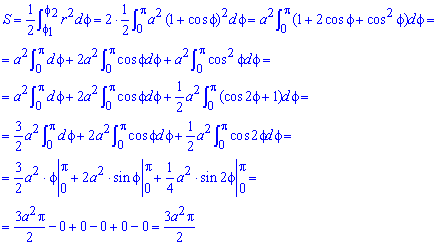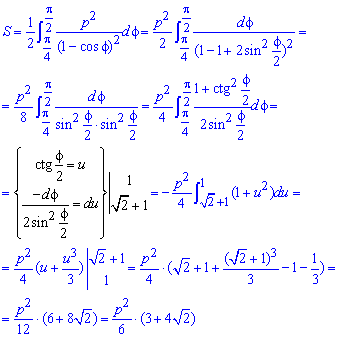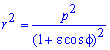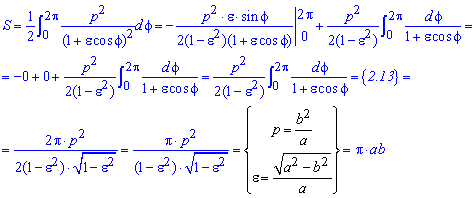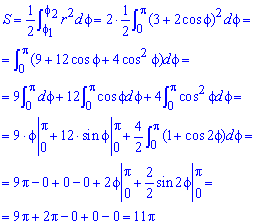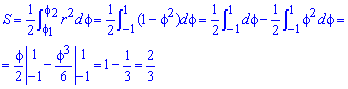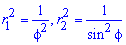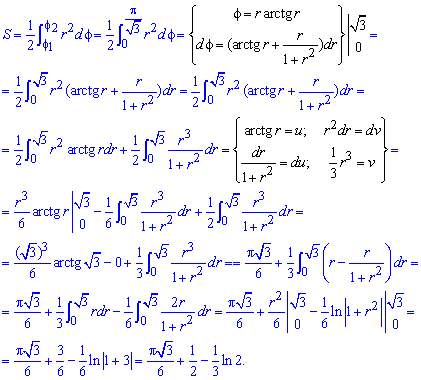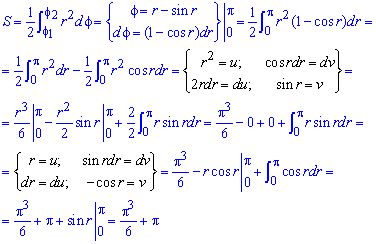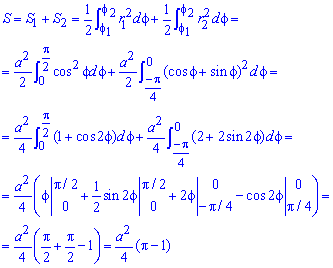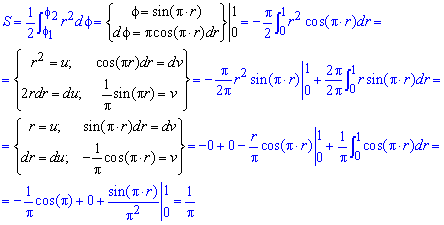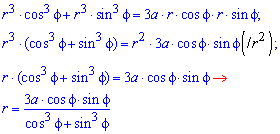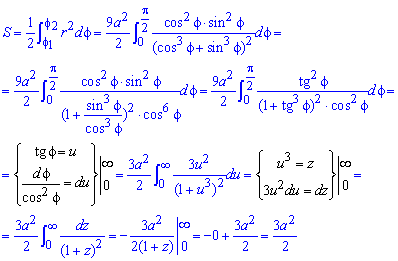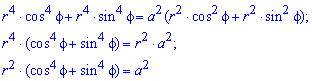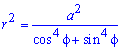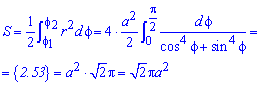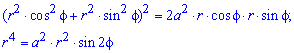Расчет площади пересечения окружностей методом Монте-Карло

Итак, моя задача заключалась в необходимости вычисления площади фигуры, являющейся пересечением окружностей, с последующей реализацией на языке JavaScript. Площадь под графиком – это интеграл. Интегрирование методом Монте-Карло достаточно широко известно, но, как многие верно заметят, его применение требует некоторого обоснования. За подробностями прошу под кат.
Обоснование
Задача расчета площади пересечения двух окружностей является тривиальной геометрической задачей (координаты центров окружностей и их радиусы нам известны). Площадь пересечения двух окружностей – это сумма площадей соответствующих сегментов этих окружностей. Есть решения для расчета площади пересечения двух, трех, четырех окружностей в различных частных случаях.
А вот решения общего случая для пересечения даже трех окружностей уже далеко не так тривиальны. В процессе поиска я нашел даже исследования по расчету площади пересечения N окружностей, однако они настолько же интересны, насколько и сложны.
Здесь на сцену выходит метод Монте-Карло. Благодаря современным компьютерным мощностям этот метод позволяет провести большое количество статистических испытаний, на основе результатов которых делается обобщение.
Итак, алгоритм расчета площади любой фигуры методом Монте-Карло сводится к следующему:
- Фигура вписывается в прямоугольник. Координаты сторон прямоугольника известны, значит, известна его площадь.
- Псевдослучайным образом внутри прямоугольника генерируется большое количество точек. Для каждой точки определяется, попала ли точка внутрь исходной фигуры или нет.
- В результате площадь исходной фигуры вычисляется исходя из обычной пропорции: отношение количества точек, попавших в фигуру, к общему количеству сгенерированных точек равно отношению площади фигуры к площади ограничивающего ее прямоугольника.
Последняя проблема, которую надо решить, заключается в том, что каким-то образом необходимо определять, попала ли точка внутрь исходной фигуры. В моем случае данная задача решается достаточно просто, поскольку моя фигура состоит из окружностей, координаты центров и радиусы которых известны.
Реализация задачи на JavaScript
Пара гвоздей в метод Бутстрапа
Если говорить именно о методе Бутстрапа, то мое личное мнение заключается в том, что случайная генерация набора данных по имеющемуся набору в общем случае не может служить для оценки закономерностей, поскольку сгенерированная информация не является достоверной. В общем, это же, только более умными (и нередко более резкими) словами, говорят и многие авторы, например, Орлов в своем учебнике по Эконометрике.
Как найти площадь пересечения трех окружностей
Как найти площадь пересечения 3-ех окружностей?
Вопрос решен и закрыт.
Лучший ответ
Mr.Nagel 8 (144456) 13 97 437 10 лет
Ответы
Виталька 5 (2724) 3 7 10 лет
Похожие вопросы
Есть часы.
Ободок — окружность.
Циферблат — круг.
Окружность — то, что рисует циркуль.
Чтобы получить круг, нужно закрасить пространство внутри окружности.
Кольцо, края кружки, колодец — окружность.
Круглый стол, монета — круг.
Расчет площади пересечения окружностей методом Монте-Карло

Итак, моя задача заключалась в необходимости вычисления площади фигуры, являющейся пересечением окружностей, с последующей реализацией на языке JavaScript. Площадь под графиком – это интеграл. Интегрирование методом Монте-Карло достаточно широко известно, но, как многие верно заметят, его применение требует некоторого обоснования. За подробностями прошу под кат.
Обоснование
Задача расчета площади пересечения двух окружностей является тривиальной геометрической задачей (координаты центров окружностей и их радиусы нам известны). Площадь пересечения двух окружностей – это сумма площадей соответствующих сегментов этих окружностей. Есть решения для расчета площади пересечения двух, трех, четырех окружностей в различных частных случаях.
А вот решения общего случая для пересечения даже трех окружностей уже далеко не так тривиальны. В процессе поиска я нашел даже исследования по расчету площади пересечения N окружностей, однако они настолько же интересны, насколько и сложны.
Здесь на сцену выходит метод Монте-Карло. Благодаря современным компьютерным мощностям этот метод позволяет провести большое количество статистических испытаний, на основе результатов которых делается обобщение.
Итак, алгоритм расчета площади любой фигуры методом Монте-Карло сводится к следующему:
- Фигура вписывается в прямоугольник. Координаты сторон прямоугольника известны, значит, известна его площадь.
- Псевдослучайным образом внутри прямоугольника генерируется большое количество точек. Для каждой точки определяется, попала ли точка внутрь исходной фигуры или нет.
- В результате площадь исходной фигуры вычисляется исходя из обычной пропорции: отношение количества точек, попавших в фигуру, к общему количеству сгенерированных точек равно отношению площади фигуры к площади ограничивающего ее прямоугольника.
Последняя проблема, которую надо решить, заключается в том, что каким-то образом необходимо определять, попала ли точка внутрь исходной фигуры. В моем случае данная задача решается достаточно просто, поскольку моя фигура состоит из окружностей, координаты центров и радиусы которых известны.
Реализация задачи на JavaScript
Пара гвоздей в метод Бутстрапа
Если говорить именно о методе Бутстрапа, то мое личное мнение заключается в том, что случайная генерация набора данных по имеющемуся набору в общем случае не может служить для оценки закономерностей, поскольку сгенерированная информация не является достоверной. В общем, это же, только более умными (и нередко более резкими) словами, говорят и многие авторы, например, Орлов в своем учебнике по Эконометрике.
Как найти площадь пересечения трех окружностей
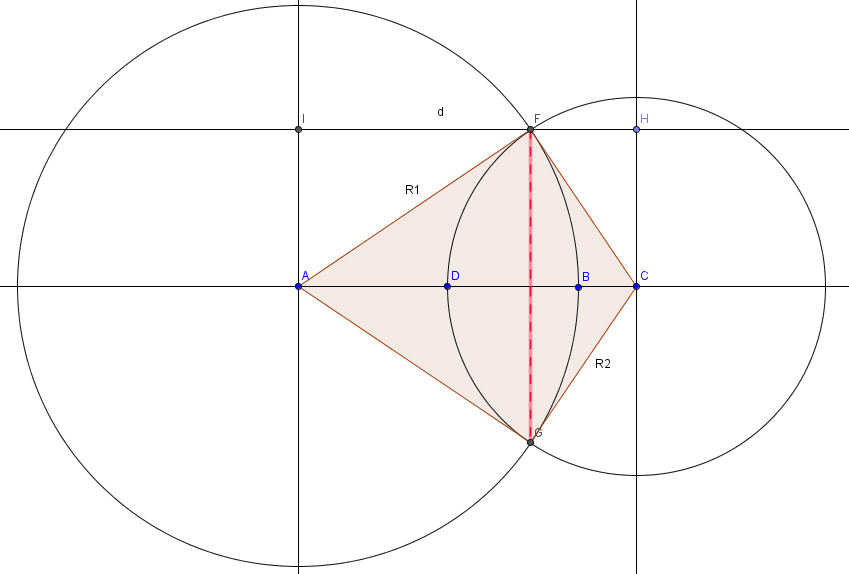
Позволяет рассчитать площадь пересечения двух окружностей произвольных радиусов.
Используются достаточно простые формулы, которые элементарно доказываются.
Дополнительно есть калькулятор, который высчитывает координаты пересечения двух окружностей
Площадь пересечения двух окружностей состоит из двух сегментов FDG и FBG
Вывести формулу расчета площади пересечения двух окружностей можно из двух общеизвестных формул и знаний решения треугольника:
Формулы сектора окружности
и длина хорды окружности
По известным сторонам треугольника AFС определяем высоту на сторону AC.
Удвоением этой высоты мы получаем длину хорды, после этого узнаем угол альфа по второй формуле.
По известным сторонам треугольника AFG узнаем его площадь. Вычитаем её из площади сектора окружности, ведь угол альфа нам уже известен.
И получаем площадь сегмента FBG
Подобным образом вычисляем FDG
Это лишь один из способов решения задачи вычисления площади пересечения двух окружностей.
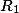
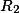
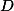
Пример
Хотим узнать площадь пересечения двух окружностей радиусом в 1 и расстоянием между центрами 0.8079455
Пишем okr 1 1 0.8079455
Площадь двух пересекающихся окружностей равна = 1.5707963388681
Первая окружность радиус 4, вторая окружность радиус 2, расстоянием между центрами 3
Пишем okr 4 2 3
Площадь двух пересекающихся окружностей равна = 9.5701994729833
Первая окружность радиус 4, вторая окружность радиус 2, расстоянием между центрами 0
Как найти площадь пересечения 3-ех окружностей?
Вопрос решен и закрыт.
Лучший ответ
Mr.Nagel 8 (144459) 13 97 438 10 лет
Ответы
Виталька 5 (2724) 3 7 10 лет
Похожие вопросы
Есть часы.
Ободок — окружность.
Циферблат — круг.
Окружность — то, что рисует циркуль.
Чтобы получить круг, нужно закрасить пространство внутри окружности.
Кольцо, края кружки, колодец — окружность.
Круглый стол, монета — круг.
http://b4.cooksy.ru/articles/kak-nayti-ploschad-peresecheniya-treh-okruzhnostey
http://irc.lv/qna/%D0%9A%D0%B0%D0%BA_%D0%BD%D0%B0%D0%B9%D1%82%D0%B8_%D0%BF%D0%BB%D0%BE%D1%89%D0%B0%D0%B4%D1%8C_%D0%BF%D0%B5%D1%80%D0%B5%D1%81%D0%B5%D1%87%D0%B5%D0%BD%D0%B8%D1%8F_3_%D0%B5%D1%85_%D0%BE%D0%BA%D1%80%D1%83%D0%B6%D0%BD%D0%BE%D1%81%D1%82%D0%B5%D0%B9
Светило науки — 7309 ответов — 165986 раз оказано помощи
1. Площадь этой фигуры = разности между площадью большего круга и площадью меньшего круга.
S₁= π15²=225π
S₂=π3²=9π
S₃=225-9=216 квадратных единиц измерения
———————-
(5, 12, 13) — Пифагорова тройка. Треугольник, длины сторон которого равны пифагоровым числам, является прямоугольным. Но мы помним, как правило, только сочетание 3, 4, 5.
Поэтому и даю решение через формулу Герона.
Этот параллелограмм АС делит на 2 равных треугольника.
Их стороны 5,13 и 12.
Площадь треугольника по формуле Герона равна корню из произведения разностей полупериметра треугольника (p) и каждой из его сторон (a, b, c):
S= √ {p (p−a) (p−b) (p−c)}
р =(5+13+12):2=30:2=15
Подставьте значения сторон в формулу и получите, что площадь одного треугольника 30 , а площадь параллелограмма
2*30=60 квадратных единиц измерения
(С формулой Герона Вы уже знакомы. Можно решить задачу и через нахождение высоты с помощью теоремы Пифагора, но это несколько сложнее и значительно дольше. В итоге получим, что этот параллелограмм — прямоугольник. Его высота — 5, и площадь равна 5*12=60)
—————————

Расчет площади пересечения окружностей методом Монте-Карло
Время на прочтение
4 мин
Количество просмотров 45K

Итак, моя задача заключалась в необходимости вычисления площади фигуры, являющейся пересечением окружностей, с последующей реализацией на языке JavaScript. Площадь под графиком – это интеграл. Интегрирование методом Монте-Карло достаточно широко известно, но, как многие верно заметят, его применение требует некоторого обоснования. За подробностями прошу под кат.
Обоснование
Задача расчета площади пересечения двух окружностей является тривиальной геометрической задачей (координаты центров окружностей и их радиусы нам известны). Площадь пересечения двух окружностей – это сумма площадей соответствующих сегментов этих окружностей. Есть решения для расчета площади пересечения двух, трех, четырех окружностей в различных частных случаях.
А вот решения общего случая для пересечения даже трех окружностей уже далеко не так тривиальны. В процессе поиска я нашел даже исследования по расчету площади пересечения N окружностей, однако они настолько же интересны, насколько и сложны.
Здесь на сцену выходит метод Монте-Карло. Благодаря современным компьютерным мощностям этот метод позволяет провести большое количество статистических испытаний, на основе результатов которых делается обобщение.
Итак, алгоритм расчета площади любой фигуры методом Монте-Карло сводится к следующему:
- Фигура вписывается в прямоугольник. Координаты сторон прямоугольника известны, значит, известна его площадь.
- Псевдослучайным образом внутри прямоугольника генерируется большое количество точек. Для каждой точки определяется, попала ли точка внутрь исходной фигуры или нет.
- В результате площадь исходной фигуры вычисляется исходя из обычной пропорции: отношение количества точек, попавших в фигуру, к общему количеству сгенерированных точек равно отношению площади фигуры к площади ограничивающего ее прямоугольника.
Последняя проблема, которую надо решить, заключается в том, что каким-то образом необходимо определять, попала ли точка внутрь исходной фигуры. В моем случае данная задача решается достаточно просто, поскольку моя фигура состоит из окружностей, координаты центров и радиусы которых известны.
Реализация задачи на JavaScript
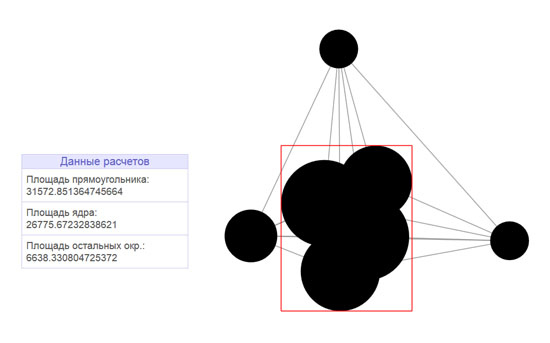
Рисование окружностей делалось средствами замечательной библиотеки D3.js. Алгоритм начального взаимного расположения окружностей выходит за рамки данной статьи, поэтому примем начальное расположение как данность.
Собираем массив пересечений пар окружностей
var nodes = d3.selectAll("circle.node");
var squares = [];
var intersections = [];
nodes.each(function(node){
// считаем радиус и площадь окружности
var r = this.r.baseVal.value;
var s = 3.14159*r*r;
squares.push({node: node, square: s, r: r});
// ищем пересечения пар окружностей
nodes.each(function(node2){
// расстояние между центрами и сумма радиусов
var center_dist = Math.sqrt(Math.pow(node.x-node2.x, 2)+(Math.pow(node.y-node2.y, 2)));
var radius_sum = r + this.r.baseVal.value;
if(center_dist <= radius_sum && node.index != node2.index){
// окружности пересекаются. проверить, что это пересечение найдено впервые
node.r = r;
node2.r = this.r.baseVal.value;
if(isNewIntersection(intersections, node, node2))
intersections.push({node1: node, node2: node2, center_dist: center_dist});
}
});
});
Считаем площадь фигуры
var areaCalculator = {
intersections: [], // массив пересечений, устанавливается снаружи
frame: {}, // рамка вокруг фигуры
circles: [], // массив окружностей
figureArea: 0, // искомая площадь фигуры
monteCarlo:
function(p){
// получаем массив окружностей из пересечения
var circles = [];
var x1_, y1_, x2_, y2_; // координаты сторон прямоугольника
var inCirclesArr = function(node){
for(var j=0; j<circles.length; j++){
if(circles[j].index==node.index){
return true;
}
}
return false;
};
for(var i=0; i<this.intersections.length; i++){
if(!inCirclesArr(this.intersections[i].node1)){
circles.push(this.intersections[i].node1);
}
if(!inCirclesArr(this.intersections[i].node2)){
circles.push(this.intersections[i].node2);
}
}
this.circles = circles;
circles.sort(function(a,b){
return a.x-a.r > b.x-b.r ? 1 : -1;
});
x1_ = circles[0].x-circles[0].r;
circles.sort(function(a,b){
return a.x+a.r < b.x+b.r ? 1 : -1;
});
x2_ = circles[0].x+circles[0].r;
circles.sort(function(a,b){
return a.y-a.r > b.y-b.r ? 1 : -1;
});
y1_ = circles[0].y-circles[0].r;
circles.sort(function(a,b){
return a.y+a.r < b.y+b.r ? 1 : -1;
});
y2_ = circles[0].y+circles[0].r;
this.frame.x1 = x1_;
this.frame.x2 = x2_;
this.frame.y1 = y1_;
this.frame.y2 = y2_;
this.frame.area = (x2_-x1_)*(y2_-y1_);
// рисуем прямоугольник
paintRect(this.frame);
// p - количество генерируемых точек. В примере использовалось 100.000, чего хватило для приемлемой точности
var p_positive = 0; // количество точек попавших в фигуру
// генерируем p точек для определения площади фигуры
for(var i=0; i<p; i++){
var x_rand = Math.random()*(x2_-x1_)+x1_;
var y_rand = Math.random()*(y2_-y1_)+y1_;
var yes = false;
for(var j=0; j<circles.length; j++) {
if(!yes && (
(circles[j].x-circles[j].r) <= x_rand &&
(circles[j].x+circles[j].r) >= x_rand &&
(circles[j].y-circles[j].r) <= y_rand &&
(circles[j].y+circles[j].r) >= y_rand )
){
yes = true;
p_positive++;
}
}
}
// площадь фигуры = площадь прямоугольника*кол-во точек внутри фигуры / общее кол-во точек
this.figureArea = this.frame.area*p_positive/p;
}
};
Пара гвоздей в метод Бутстрапа
Если говорить именно о методе Бутстрапа, то мое личное мнение заключается в том, что случайная генерация набора данных по имеющемуся набору в общем случае не может служить для оценки закономерностей, поскольку сгенерированная информация не является достоверной. В общем, это же, только более умными (и нередко более резкими) словами, говорят и многие авторы, например, Орлов в своем учебнике по Эконометрике.
Заключение
Методы Монте-Карло являются вполне жизнеспособными и весьма полезными в некоторых случаях, как, например, в моем. Возможности современных компьютеров, даже обычных настольных машин, вполне позволяют оперировать подобными статистическими методами с достаточно большим количеством испытаний и, соответственно, получать достаточную точность результата. Но при всем этом, конечно, они являются лишь упрощением модели и не могут претендовать на что-то большее.
Площадь S криволинейного сектора, ограниченного непрерывной кривой r=r(f) и двумя лучами f=f1 и f=f2, где f1<f2 равняется половине определенного интегралу от квадрата радиуса кривой, проинтегрированного в пределах изменения угла
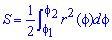
Для запоминания основных моментов схема интегрирования и нахождения площадей из примера в пример будет повторяться. Сами ррешеня по возможности будут проиллюстрированы графиками исследуемых кривых.
Найти площади фигур, ограниченных кривыми, заданными в полярных координатах
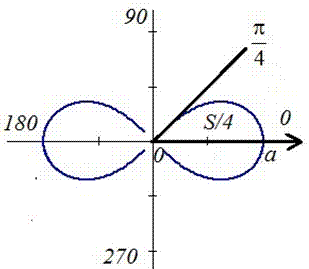
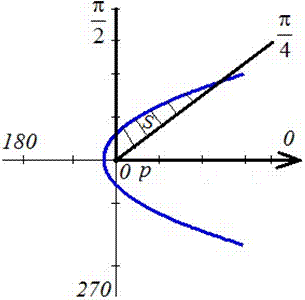
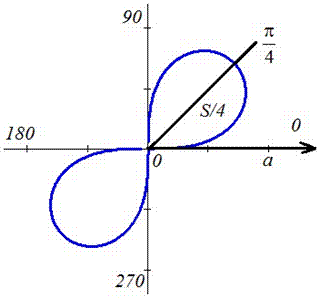
Пример 2.106 (2418) Вычислить площадь фигуры, ограниченной кривыми r2=a2*cos(2f) (лемниската Бернулли).
Вычисление: Лемниската Бернулли — геометрическое место точек, произведение расстояний от которых до двух фиксированных точек (фокусов) остается постоянным и равняется квадрату половины расстояния между фокусами.
Запишем подинтегральную функцию: r2=a2*cos(2f) (известна за условием).
Найдем пределы интегрирования:
задана кривая замкнутая, симметричная относительно прямых r*cos(f)=0 и r*sin(f)=0.
Наведем график лемнискаты Бернулли
Поскольку заданная функция осями координат делится на четыре равных части и достигает своих критических значений при f1=0 (r=a) и f2=p/4 (r=0), то площадь фигуры вычислим для одной части лемнискаты, а результат умножим на 4.
Найдем площадь фигуры интегрированиям по углу
Площадь измеряется в единицах квадратных, однако в этом и следующих примерах размерности наводить не будем, хотя о них помним.
Пример 2.107 (2419) Найти площадь фигуры, ограниченной кривыми r=a* (1+cos(f)) — кардиоида.
Вычисление: Кардиоида — плоская линия, которая описывается фиксированной точкой круга, который катится по неподвижному кругу с таким же радиусом a.
Записываем подинтегральную функцию: r2=a2*(1+cos(f))2.
Находим пределы интегрирования: кривая замкнутая, симметричная относительно прямой r*sin(f) =0.
Поскольку заданная функция осями координат делится на две равных части и достигает своих критических значений при f1=0 (r=2a) и f2=p (r=0), то площадь фигуры вычислим для половины кардиоиды, а результат умножим на 2.
График кардиоиды имеет вид
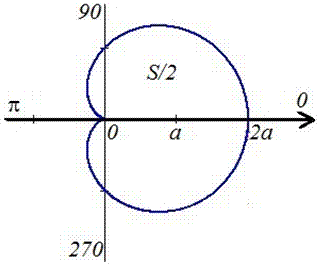
Вычислим площадь фигуры, которая ограничена заданной кривой, интегрированием:
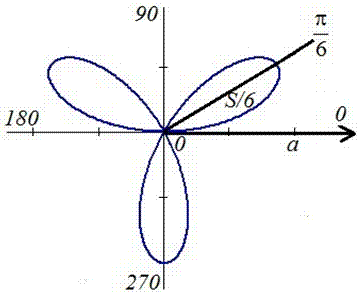
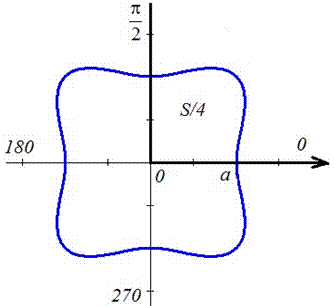
Пример 2.108 (2420) Найти площадь фигуры, ограниченной кривой r=a*sin(f) -трилисник.
Вычисление: Подносим функцию к квадрату, чтобы получить подинтегральную функцию:
r2=a2*sin2(f).
График трилистника в полярной системе координат
Установим пределы интегрирования:
Поскольку заданный график функции делится на шесть равных частей (полупелюсток) и достигает своих критических значений при f1=0 (r=0) и f2=p/6 (r=a/2) то площадь фигуры вычислим для одной его части, а результат умножим на 6.
Находим площадь фигуры интегрированием по углу
Получили простую для вычислений формулу площади трилистника S=Pi*a2/4.
Пример 2.109 ( 2421) Вычислить площадь фигуры, ограниченной кривой 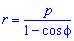
Вычисление: Подносим к квадрату уравнения кривой в полярной системе коринат (СК).
Пределы интегрирования известны f1=p/4, f2=p/2 за условием.
График фигуры, площадь которой нужно найти имеет вид
Интегрированием вычисляем площадь фигуры, которая ограничена параболой:
Для вычисления интеграла следует выполнить замену переменных, не забывая при этом , что изменяются пределы интегрирования.
Пример 2.110 ( 2422) Найти площадь фигуры, ограниченной кривой 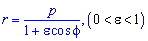
Вычисление: Запишем подинтегральную функцию:
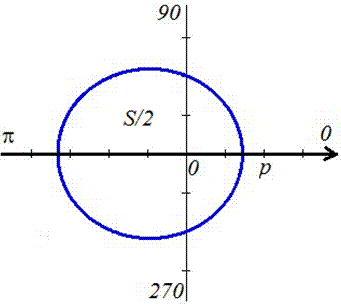
Пределы интегрирования: f1=0, f2=2p (начало и конец кривой эллипса).
График эллипса имеет вид
Находим площадь елипса, воспользовавшись следующей формулой интегрирования
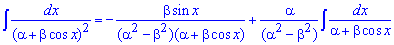
При выведении этой формулы пользовались методом интегрирования частями!
Напоследок превращаем конечную формула с помощью известных формул.
Как видим, ответы задач 2.110 и 2.87 совпадают, то есть площадь эллипса S=Pi*a*b вычислена правильно.
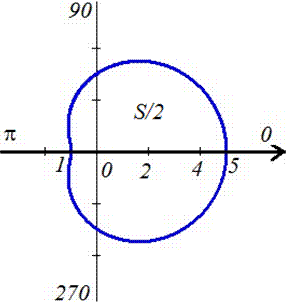
Пример 2.111 (2422.1) Найти площадь фигуры, ограниченной кривой заданной в полярных координатах r=3+2*cos(f).
Вычисление: Сначала находим подинтегральную функцию: r2=(3+2*cos(f))2.
Дальше пределы интегрирования: задана кривая замкнутая, симметричная относительно прямой r*sin(f)=0.
Ее график приведен на рисунку ниже
Поскольку задана кривая осями координат делится на две равных части и достигает своих критических значений при углах f1=0 (r=5) и f2=p (r=1), то вычислим половину площади фигуры, а результат умножим на 2.
Находим площадь фигуры через определенный интеграл
Интеграл в данном случае не тяжелый и, возведя в квадрат подинтегральную функцию и понизив квадрат косинуса, в результате вычислений получим, что площадь равна S=11*Pi.
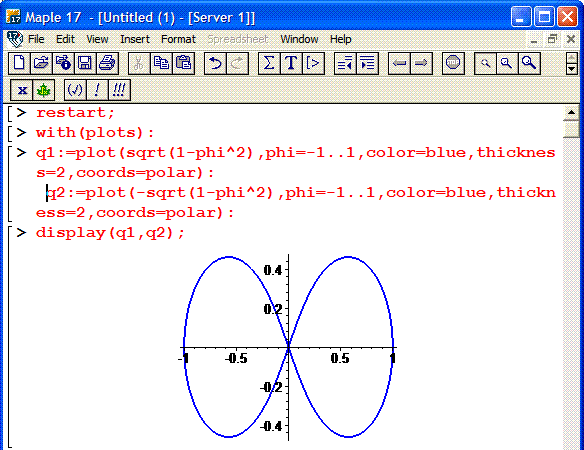
Пример 2.112 (2424.1) Найти площадь фигуры, ограниченной кривой заданной в полярных координатах r2+f2=1.
Вычисление: Выражаемый подинтегральную функцию: r2=1-f2 .
Найдем пределы интегрирования.
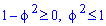
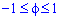
Построим график кривой в математическом пакете Maple17.
Кривая состоит из двух веток корневой функции, поэтому для корректного ее отображения используем следующий код:
> restart;
> with (plots) :
> q1:=plot(sqrt(1-phi^2),phi=-1.1, color=blue, thickness=2, coords=polar):
q2:=plot(-sqrt(1-phi^2),phi=-1.1, color=blue, thickness=2, coords=polar):
> display (q1, q2);
Фрагмент программы Maple приведен ниже
Находим площадь фигуры, которая ограничена кривой:
Интеграл в этом задании простей всех, что рассматривались.
Пример 2.113 ( 2422.2) Вычислить площадь фигуры, ограниченной кривыми 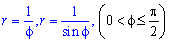
Вычисление: Выписываем подинтегральные функции:
Поскольку на промежутке интегрирования 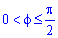
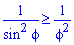
Найдем пределы интегрирования: f1=0 — особенная точка (функция направляется к безграничности) f1=p/2 (известны за условием).
Находим площадь фигуры через предел от интеграла:
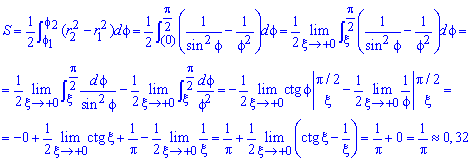
Данный пример хорошо разберите, чтобы не иметь трудностей на экзамене или модуле с подобными.
Пример 2.114 ( 2424) Вычислить площадь фигуры, ограниченной кривой 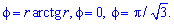
Вычисление: Запишем подинтегральную функцию: r2.
Запишем пределы интегрирования:
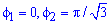
График функций имеет вид
Вычислим площадь фигуры, что приведена на графике.
Для этого сначала находим дифференциал угла f и переходим к интегрированию по радиусу.
Для нахождения интеграла применяем интегрирование частями
Интеграл достаточно трудно находится, поэтому все что содержит формула внимательно проанализируйте.
Пример 2.116 (2424.4) Найти площадь фигуры, ограниченной полярными кривыми f=r-sin(r), f=p.
Вычисление: Подинтегральную функция следующая: r2.
Пределы интегрирования: f1=0, (r=0) начало; f1=p (известно за условием).
График функции имеет вид
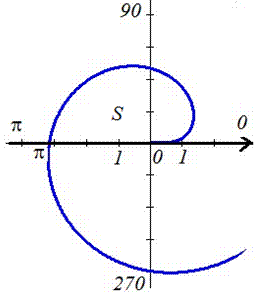
Находим площадь фигуры, применяя дважды интегрирование частями
Интеграл не слишком сложен, все переходы просьба проанализировать самостоятельно.
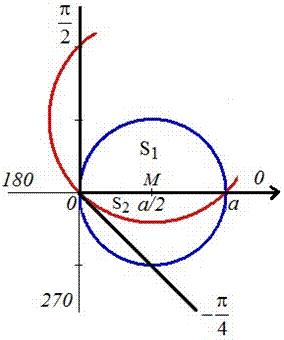
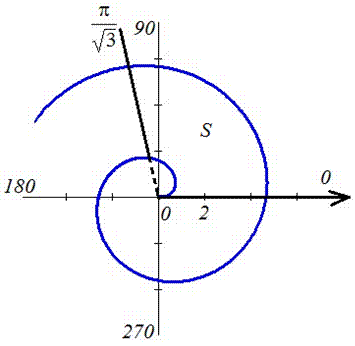
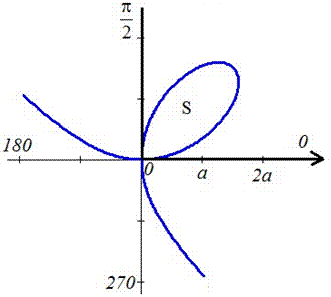
Пример 2423 Вычислить площадь фигуры, ограниченной полярными кривыми r=a*cos(f), r=a(cos(f)+sin(f)), M (a/2;0)єS.
Вычисление: Для представления фигуры, площадь которой нужно найти предварительно выполняем построение графика заданных функций
Поскольку точка M (a/2;0)єS делит искомую площадь на две части, то имеем два интеграла
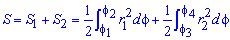
Записываем уравнение подинтегральных функций:
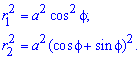
Определяем пределы интегрирования:
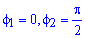
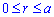
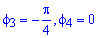
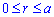
Вычисляем площадь изображенной фигуры интегрированием
Здесь воспользовались известные тригонометрические формулы для понижения степени косинусов и синусов под интегралом. Все остальное сводятся к применению простых формул интегрирования, и нахождения их значений.
Пример 2424.2 Найти площадь фигуры, ограниченной полярными кривыми f=sin(p*r), r пренадлежит [0;1].
Вычисление: Запишем подинтегральную функцию: r2.
Запишем пределы интегрирования: При росте r от 0 к 1/2 угол f растет от 0 к 1, при росте r от 1/2 к 1 угол f спадает от 1 к 0, поэтому величина интеграла в пределах r пренадлежит [0;1] имеет знак «минус».
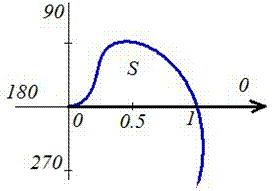
Находим площадь фигуры, предварительно перейдя к новой переменной под интегралом:
Перед интегралом (после замены переменных) поставили знак «минус», поскольку интеграл является отрицательным на этом промежутке, а площадь должна быть положительной.
Перейти к полярным координатам и найти площади фигур, ограниченных кривыми
Пример 2426 Перейти к полярным координатам и найти площадь фигуры x3+y3=3a*x*y (лист Декарта)
Вычисление: Перейдем от прямоугольной системы координат к полярной системе координат за формулами перехода:
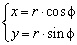
При подстановке в уравнение получим
Поднесем к квадрату, чтобы получить подинтегральную функцию:
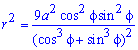
Выпишем пределы интегрирования:
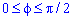
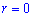
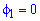
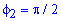
График функции имеет вид
Найдем площадь фигуры интегрированиям:
Для получения конечной формулы площади дважды применяли замену переменных под интегралом.
Внимательно разберите, как при этом изменяются пределы и эффективность методики.
Пример 2427 Перейти к полярным координатам и найти площадь фигуры x4+y4=3a2(x2+y2)
Вычисление: Переходим от прямоугольной к полярной системе координат:
Выражаемый подинтегральную функцию делением:
Запишем пределы интегрирования:
Ее график изображен на рисунку
Оси прямоугольной системы координат являются осями симметрии для фигуры, которая ограничена заданной линией, поэтому площадь найдем для симметричной части и результат умножим на 4.
Находим площадь фигуры через интеграл:
Пример 2428 Перейти к полярным координатам и найти площадь фигуры (x2+y2)2=2a2*x*y (лемниската).
Вычисление: Выполняем переход от прямоугольной к полярной системе координат:
График исследуемой кривой следующий
Запишем пределы интегрирования: учитывая симметрию точек лемнискаты относительно прямой r*sin(f) =r*cos (f) и относительно начала координат, то площадь фигуры будем искать в пределах 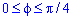
Находим площадь фигуры интегрированием:
Вычислений в этом задании минимум.
В следующих публикациях Вы найдете больше примеров на применение определенного интеграла при вычислении длины дуги, объемов фигур вращения и площадей поверхностей.
A combined figure is a geometrical shape that is the combination of many simple geometrical shapes.
To find the area of combined figures we will follow the steps:
Step I: First we divide the combined figure into its simple geometrical shapes.
Step II: Then calculate the area of these simple geometrical shapes separately,
Step III: Finally, to find the required area of the combined figure we need to add or subtract these areas.
Solved Examples on Area of combined figures:
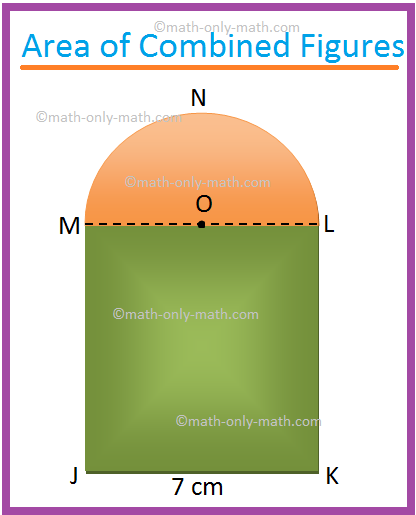
1. Find the area of the shaded region of the adjoining figure. (Use π = (frac{22}{7}))
JKLM is a square of side 7 cm. O is the centre of the
semicircle MNL.
Solution:
Step I: First we divide the combined figure into
its simple geometrical shapes.
The given combined shape is combination of a
square and a semicircle.
Step II: Then calculate the area of
these simple geometrical shapes separately.
Area of the square JKLM = 72 cm2
=
49 cm2
Area of the semicircle LNM = (frac{1}{2}) π ∙ ((frac{7}{2})^{2}) cm2 , [Since,
diameter LM = 7 cm]
=
(frac{1}{2}) ∙ (frac{22}{7}) ∙ (frac{49}{4}) cm2
=
(frac{77}{4}) cm2
=
19.25 cm2
Step III: Finally, add these areas up to get
the total area of the combined figure.
Therefore, the required area = 49 cm2 + 19.25 cm2
=
68.25 cm2.
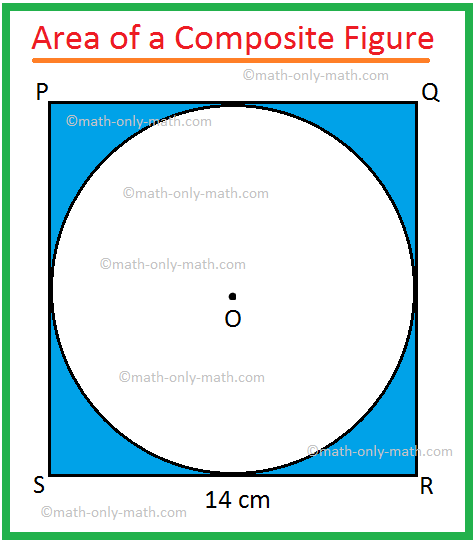
2. In the adjoining figure, PQRS is a square of side 14 cm
and O is the centre of the circle touching all sides of the square.
Find the area of the shaded region.
Solution:
Step I: First we divide the combined figure into its simple geometrical shapes.
The given combined shape is combination of a square and a circle.
Step II: Then calculate the area of these simple geometrical shapes separately.
Area of the square PQRS = 142 cm2
= 196 cm2
Area of the circle with centre O = π ∙ 72 cm2, [Since, diameter SR = 14 cm]
= (frac{22}{7}) ∙ 49 cm2
= 22 × 7 cm2
= 154 cm2
Step III: Finally, to find the required area of the combined figure we need to subtract the area of the circle from the area of the square.
Therefore, the required area = 196 cm2 — 154 cm2
= 42 cm2
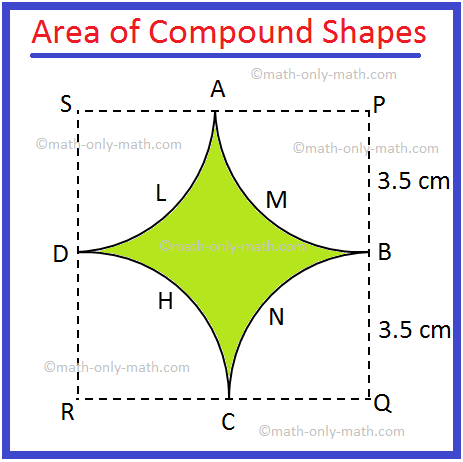
3. In the adjoining figure alongside, there are four equal quadrants of circles each of radius 3.5 cm, their centres being P, Q, R and S.
Find the area of the shaded region.
Solution:
Step I: First we divide the combined figure into its simple geometrical shapes.
The given combined shape is combination of a square and four quadrants.
Step II:Then calculate the area of these simple geometrical shapes separately.
Area of the square PQRS = 72 cm2, [Since, side of the square = 7 cm]
= 49 cm2
Area of the quadrant APB = (frac{1}{4}) π ∙ r2 cm2
= (frac{1}{4}) ∙ (frac{22}{7}) ∙ ((frac{7}{2})^{2}) cm2, [Since, side of the square = 7 cm and radius of the quadrant = (frac{7}{2}) cm]
= (frac{77}{8}) cm2
There are four quadrants and they have the same area.
So, total area of the four quadrants = 4 × (frac{77}{8}) cm2
= (frac{77}{2}) cm2
= (frac{77}{2}) cm2
Step III: Finally, to find the required area of the combined figure we need to subtract the area of the four quadrants from the area of the square.
Therefore, the required area = 49 cm2 — (frac{77}{2}) cm2
= (frac{21}{2}) cm2
= 10.5 cm2
10th Grade Math
From Areas of Combined Figures to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.