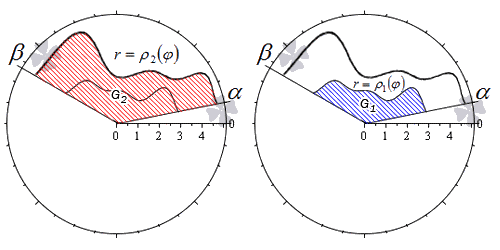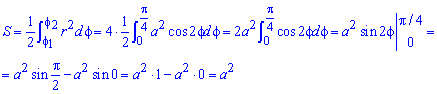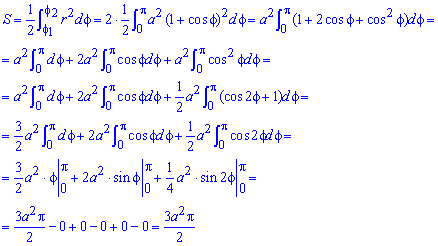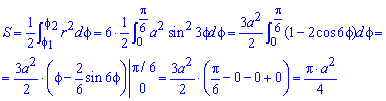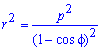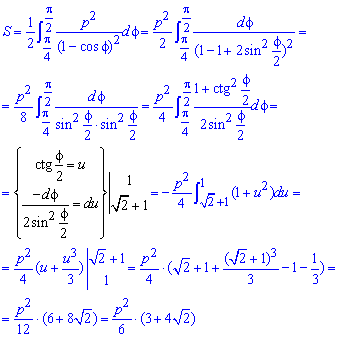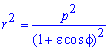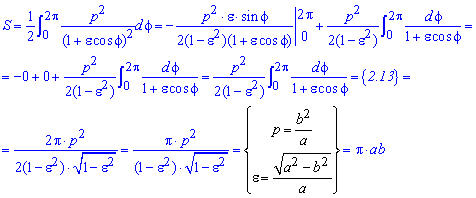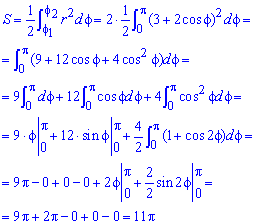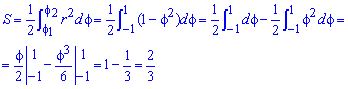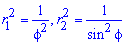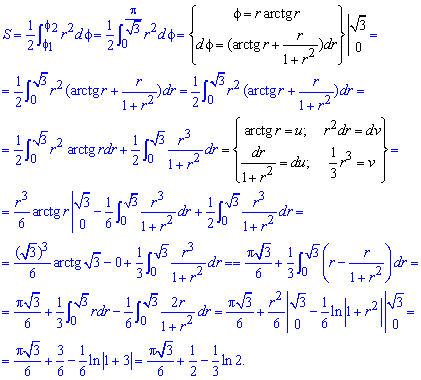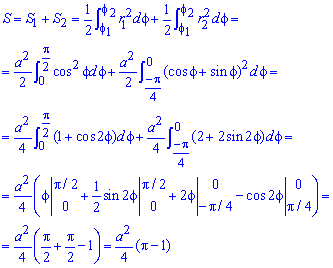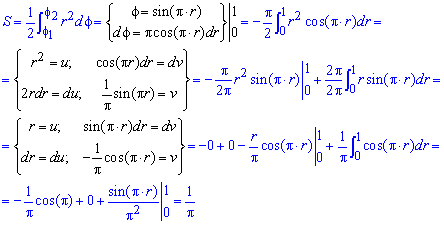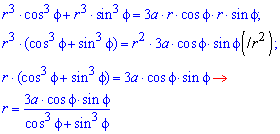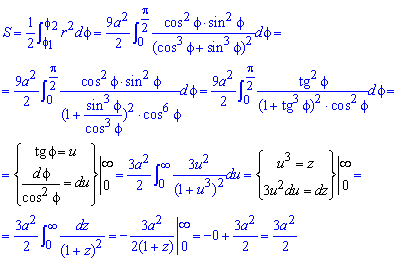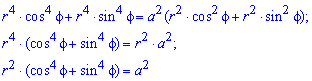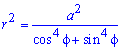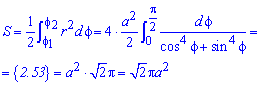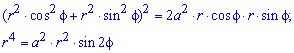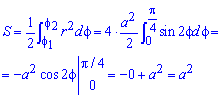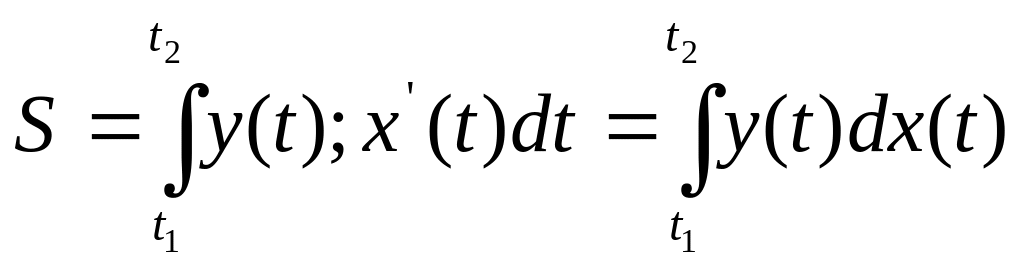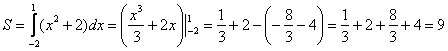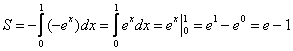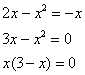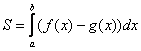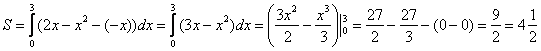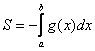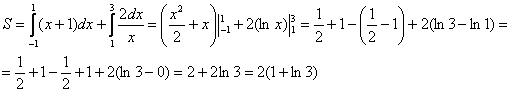Как найти площадь фигуры ограниченной окружностями - Исправление недочетов и поиск решений вместе с Examum.ru

Вычисление площади фигуры в полярных координатах

В этом разделе мы продолжим разбирать тему вычисления площадей плоских фигур. Рекомендуем тем, кто изучает темы не по порядку, сначала обратиться к статье «Геометрический смысл определенного интеграла» и разобрать способы вычисления площади криволинейной трапеции. Нам понадобится вычислять площади фигур, которые ограничены ограничены линиями y = f ( x ) , x = g ( y ) в прямоугольной системе координат. А также раздел «Свойства площади фигур», где была разобрана квадрируемость плоских фигур.

Краткий обзор статьи

Начнем с определения понятия криволинейного сектора, получим формулу для вычисления его площади. Для этого мы используем понятие определенного интеграла Дарбу.
Подробно разберем решения задач с использованием таких кривых как кардиоида, архимедова спираль и лемниската Бернулли.
В отдельную подтему мы выделили нахождение площади фигуры, которая представлена как разность двух криволинейных секторов.

Полярная система координат и криволинейный сектор

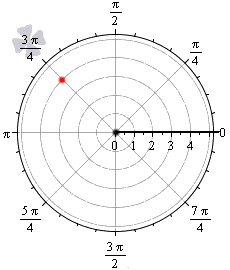
Точка, расположенная в полярной системе координат, имеет полярный угол φ 0 и полярный радиус r 0 ≥ 0 . Полярный угол φ 0 отсчитывается от полярной оси по часовой стрелке, а r 0 — это расстояние от заданной точки до начала координат.

На рисунке мы отметили начало координат (полюс) жирной черной точкой, полярная ось имеет вид луча черного цвета, а красная точка определяется углом φ 0 = 3 π 4 и расстоянием до полюса r 0 = 4 .

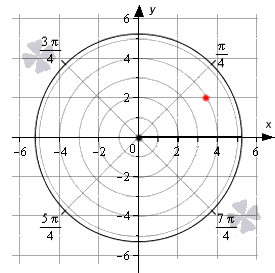
Мы можем рассматривать полярную систему координат одновременно с прямоугольной декартовой. Для этого необходимо совместить начала координат обеих систем, а ось абсцисс и полярной осью.

Задать связь полярных и декартовых координат можно соотношениями r = x 2 + y 2 φ = a r c t g y x , x ≠ 0 и обратно x = r · cos φ y = r · sin φ .

Координаты красной точки на чертеже 2 3 ; 2 . Положение этой точки задается углом φ 0 = a r c t g 2 2 3 = π 6 и расстоянием r 0 = 2 3 2 + 2 2 = 4 .

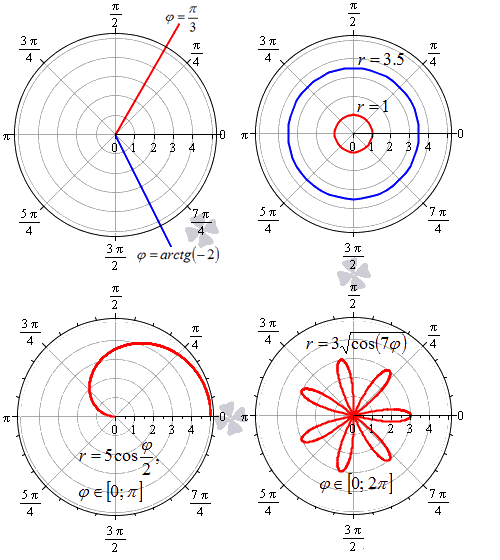
В полярной системе координат равенство φ = α задает луч, который выходит из точки начала координат и составляет угол α с полярной осью. При этом, угол α может быть задан как в радианах, так и в градусах. Полярную ось мы можем задать уравнением вида φ = 0 . Равенство r = C > 0 задает окружность с центром в начале координат, где — это радиус.

Функция r = p ( φ ) , φ ∈ α ; β определяет некоторую линию в полярных координатах.

Следует учитывать тот факт, что с позиции геометрии функция r = p ( φ ) , φ ∈ α ; β во всех случаях будет неотрицательной. Связано это с тем, что она задает расстояние от начала координат до точки для заданного значения угла φ = φ 0 ∈ α ; β . Однако мы будем встречать и отрицательные значения r = p ( φ ) функции, что зависит от отношения к данному вопросу конкретных исследователей и преподавателей.

На рисунке мы изобразили несколько примеров линий в полярной системе координат.

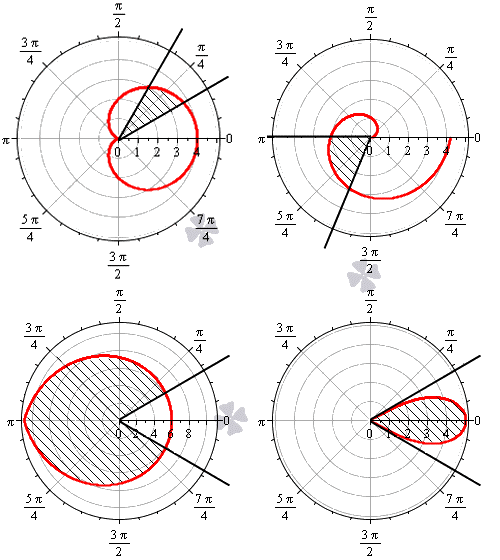
Дадим определение криволинейному сектору.

Криволинейный сектор представляет собой фигуру, которая ограничена лучами φ = α , φ = β и некоторой линией r = p ( φ ) ≥ 0 , непрерывной на участке α ; β .

На рисунке мы привели несколько примеров криволинейных секторов.

На последнем рисунке мы рассмотрели случай, когда фигура располагается между лучами φ = — π 6 , φ = π 6 , которые не являются ее границами.

Площадь криволинейного сектора — вывод формулы

Для вычисления площади криволинейного сектора мы можем вывести формулу. Для этого мы можем использовать формулу площади кругового сектора радиуса R с внутренним углом γ из школьного курса геометрии: S к р у г о в о г о с е к т о р а = γ · R 2 2 . Задаем внутренний угол γ в радианах.

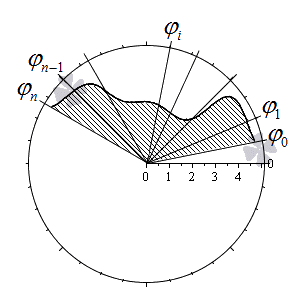
Разобьем криволинейный сектор на n частей такими лучами

φ = φ 1 , φ = φ 2 , . . . , φ = φ n — 1 , что α = φ 0 φ 1 φ 2 . . . φ n — 1 β и λ = m a x i = 1 , 2 , . . . , n φ i — φ i — 1 → 0 при n → + ∞ .

Учитывая свойства площади фигуры, мы можем представить площадь исходного криволинейного сектора S ( G ) как сумму площадей секторов S ( G i ) на каждом из участков разбиения:

S ( G ) = ∑ i = 1 n S ( G i )

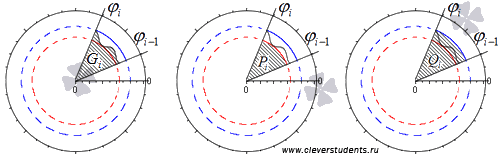
Обозначим наибольшее и наименьшее значения функции r = p ( φ ) на i -ом отрезке φ i — 1 ; φ i , i = 1 , 2 , . . . , n как R m i n i и R m a x i . На каждом из отрезков построим по два круговых сектора P i и Q i с максимальным и минимальным радиусами R m i n i и R m a x i соответственно.

Фигуры, которые являются объединением круговых секторов Q i , i = 1 , 2 , . . . , n ; P i , i = 1 , 2 , . . . , n , обозначим как P и Q соответственно.

Их площади будут равны S ( P ) = ∑ i = 1 n S ( P i ) = ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i — φ i — 1 и S ( Q ) = ∑ i = 1 n S ( Q i ) = ∑ i = 1 n 1 2 ( R m a x i ) 2 · φ i — φ i — 1 , причем S ( P ) ≤ S ( G ) ≤ S ( Q ) .

Так как функция r = p φ непрерывна на отрезке α ; β , то функция 1 2 p 2 φ будет непрерывна на этом отрезке. Если рассматривать S ( P ) и S ( Q ) для этой функции как нижнюю и верхнюю суммы Дарбу, то мы можем прийти к равенству:

lim λ → 0 S ( P ) = lim λ → 0 S ( Q ) = S ( G ) ⇒ S ( G ) = lim λ → 0 ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i — φ i — 1 = = lim λ → 0 ∑ i = 1 n 1 2 ( R m a x i ) · φ i — φ i — 1 = 1 2 ∫ β α p 2 φ d φ

Формула для определения площади криволинейного сектора имеет вид:

S ( G ) = 1 2 ∫ β α p 2 φ d φ

Примеры вычисления площади криволинейного сектора

Рассмотрим алгоритмы вычисления площади криволинейного сектора с полярной системе координат на конкретных примерах.

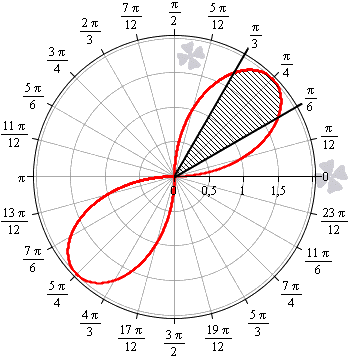
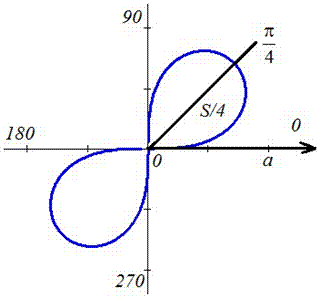
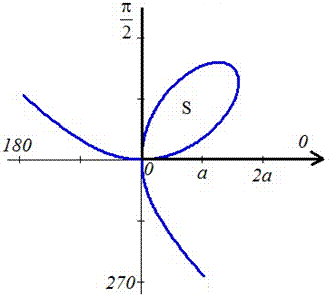
Необходимо вычислить площадь плоской фигуры в полярных координатах, которая ограничена линией r = 2 sin 2 φ и лучами φ = π 6 , φ = π 3 .

Решение

Для начала, изобразим описанную в условии задачи фигуру в полярной системе координат. Функция r = 2 sin ( 2 φ ) положительна и непрерывна на отрезке φ ∈ π 6 , π 3 .

Полученная фигура является криволинейным сектором, что позволяет нам применить формулу для нахождения площади этого сектора.

S ( G ) = 1 2 ∫ π 6 π 3 ( 2 sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 ( sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 · 1 — cos 4 φ 2 d φ = ∫ π 6 π 3 ( 1 — cos ( 4 φ ) ) d φ = φ — 1 4 sin ( 4 φ ) π 6 π 3 = = π 3 — 1 4 sin 4 π 3 — π 6 — 1 4 sin 4 π 6 = π 6 + 3 4

Ответ: S ( G ) = π 6 + 3 4

Задача упрощается в тех случаях, когда лучи φ = φ 1 , φ = φ 2 , ограничивающие фигуру, заданы. Тогда нам не нужно задумываться о пределах интегрирования при проведении вычисления площади.

Чаще встречаются задачи, где фигуру ограничивает лишь кривая r = p ( φ ) . В этих случаях применить формулу S ( G ) = 1 2 ∫ α β p 2 ( φ ) d φ сразу не получится. Для начала придется решить неравенство p ( φ ) ≥ 0 для нахождения пределов интегрирования. Так мы можем поступить в тех случаях, когда функция r = p φ неотрицательная. В противном случае нам придется ориентироваться только на область определения и период функции.

Необходимо вычислить площадь фигуры, которая ограничена кривой в полярных координатах r = — 3 · cos 3 φ .

Решение

Функция определена для всех действительных значений аргумента. Решим неравенство — 3 · cos 3 φ ≥ 0 :

— 3 · cos 3 φ ≥ 0 ⇔ cos 3 φ ≤ 0 ⇔ cos φ ≤ 0 ⇔ ⇔ π 2 + 2 πk ≤ φ ≤ 3 π 2 + 2 πk , k ∈ Z

Построим функцию в полярных координатах на отрезке φ ∈ π 2 ; 3 π 2 (при k = 0 ). Для других значений k в силу периодичности косинуса мы будем получать ту же самую кривую.

Применим формулу для вычисления площади фигуры в полярных координатах. В качестве нижнего и верхнего предела можно брать π 2 + 2 πk и 3 π 2 + 2 πk соответственно для любого целого значения k .

S ( G ) = 1 2 ∫ π 2 3 π 2 ( — 3 · cos 3 φ ) d φ = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ

Для того, чтобы получить ответ, нам необходимо вычислить полученный определенный интеграл. Для этого мы можем использовать формулу Ньютона-Лейбница. Первообразную для формулы Ньютона-Лейбница мы можем с помощью рекуррентной формулы вида K n ( x ) = sin x · cos n — 1 ( x ) n + n — 1 n K n — 2 ( x ) , где K n ( x ) = ∫ cos n ( x ) d x .

∫ cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 6 ∫ cos 4 φ d φ = = sin φ · cos 5 φ 6 + 5 6 sin φ · cos 3 φ 4 + 3 4 cos 2 φ d φ = = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 24 sin φ · cos φ 2 + 1 2 ∫ cos 0 φ d φ = = ∫ π 2 3 π 2 cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 sin φ · cos φ 48 + 15 φ 48 π 2 3 π 2 = = 15 48 · 3 π 2 — 15 48 · π 2 = 5 π 16

Таким образом, искомая площадь фигуры, ограниченной линией в полярной системе координат, равна S ( G ) = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ = 9 2 · 5 π 16 = 45 π 32 .

Ответ: S ( G ) = 45 π 32

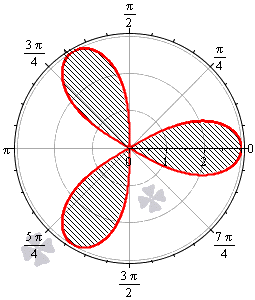
В тех случаях, когда в полярной системе координат задается множество кривых, которые по форме напоминают листья клевера или цветка, площадь фигур, ограниченных этими кривыми, часто одинаковы. В этих случаях можно вычислить площадь одного «лепестка» и умножить ее на количество криволинейных фигур.

Необходимо вычислить площадь плоской фигуры в полярной системе координат, которая ограничена линией r = 3 · cos ( 3 φ ) .

Решение

Найдем область определения, исходя из того, что эта функция неотрицательна для любого φ из области определения.

cos ( 3 φ ) ≥ 0 ⇔ — π 2 + 2 πk ≤ 3 φ ≤ π 2 + 2 πk , k ∈ Z — π 6 + 2 π 3 k ≤ φ ≤ π 6 + 2 π 3 k , k ∈ Z

Таким образом, период функции r = 3 · cos 3 φ равен 2 π 3 . Это значит, что фигура состоит из трех областей одинаковой площади.

Построим фигуру на графике.

Вычислим площадь одного участка, расположенного на интервале φ ∈ π 2 ; 5 π 6 (при k = 1 ):

1 2 ∫ π 2 5 π 6 9 cos ( 3 φ ) d φ = 1 2 · 3 sin ( 3 φ ) π 2 5 π 6 = 3 2 sin 3 · 5 π 6 — sin 3 · π 2 = 3 2 ( 1 — ( — 1 ) = 3

Ответ: Площадь всей фигуры будет равна площади найденного участка, умноженной на 3.

Аналогичным образом можно найти площади фигур, имеющих сходное строение. Примером может служить лемниската Бернулли.

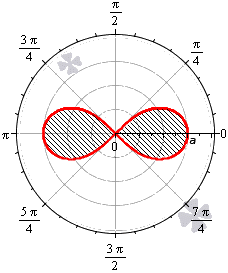
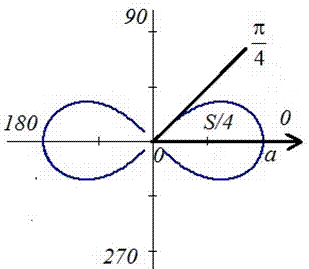
Площадь фигуры, которую ограничивает лемниската Бернулли

Лемниската Бернулли задается уравнением r = α · cos 2 φ где a – положительное число, влияющее на размер линии (но не на конфигурацию, схожую с символом бесконечности). Лемниската Бернулли строится при — π 4 + π · k ≤ φ ≤ π 4 + π · k , k ∈ Z .

Лемниската служит границей фигуры, которую можно представить как два равных по площади участка.

Для вычисления площади используем нужную формулу:

S ( G ) = 2 · 1 2 ∫ — π 4 π 4 a 2 cos ( 2 φ ) 2 φ = a 2 2 ( sin ( 2 φ ) ) — π 4 π 4 = = a 2 2 sin 2 · π 4 — sin 2 · — π 4 = a 2

Получается, что площадь фигуры, которую ограничивает лемниската Бернулли, равна квадрату коэффициента a .

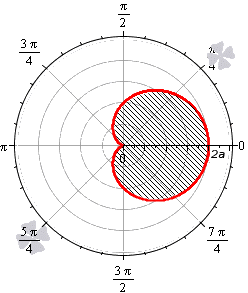
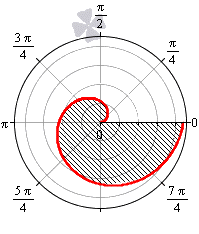
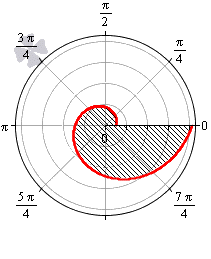
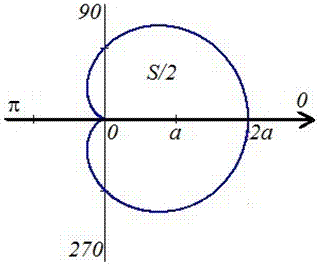
Площадь фигуры, границей которой является кардиоида

В полярной системе координат кардиоида задается уравнением вида r = 2 a ( 1 + cos φ ) . В этом уравнении a – некоторое положительное число. Задающая кардиоиду функция является периодической с периодом 2 π . Она определена для всех действительных значений угла. Это значит, что для вычисления площади нижним пределом интегрирования мы будем считать любое число, а верхним, то, которое на 2 π больше нижнего.

Вычислим площадь фигуры, ограниченной кардиоидой r = 2 a ( 1 + cos φ ) , для φ ∈ 0 ; 2 π :

S ( G ) = 1 2 ∫ 0 2 π ( 2 a ( 1 + cos φ ) ) 2 d φ = 2 a 2 ∫ 0 2 π ( 1 + 2 cos φ + cos 2 φ ) d φ = = 2 a 2 ∫ 0 2 π 1 + 2 cos φ + 1 + cos 2 φ 2 d φ = = 2 a 2 ∫ 0 2 π 3 2 + 2 cos φ + cos ( 2 φ ) 2 d φ = = 2 a 2 3 2 φ + 2 sin φ + 1 4 sin 2 φ 0 2 π = 6 π · a 2

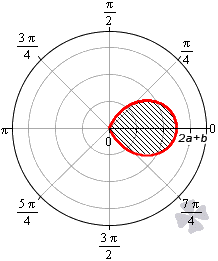
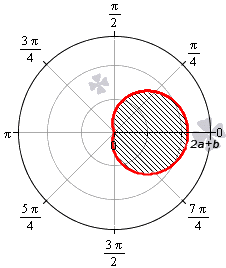
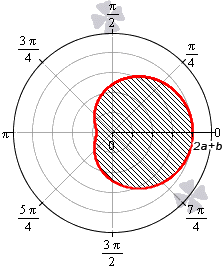
Площадь фигуры, которую ограничивает улитка Паскаля

В полярной системе координат улитка Паскаля может быть задана уравнением r = b + 2 a · cos φ . В этом уравнении a – это некоторое положительное число, b – любое действительное число. Кардиоиду можно рассматривать как частный случай улитки Паскаля. Получить кардиоиду можно при b = 2 a .

Улитка Паскаля в зависимости от значений параметров a и b может принимать различный вид. В данном разделе мы рассмотрим случаи, когда функцию r неотрицательная.

При b — 2 a функция r = b + 2 a · cos φ будет отрицательной для любого значения угла φ .

При b = — 2 a улитка Паскаля имеет вид точки, которая совпадает с полюсом.

При — 2 a b 0 функция r = b + 2 a · cos φ неотрицательна для φ ∈ — a r c cos — b 2 a + 2 πk ; arccos — b 2 a + 2 πk , k ∈ Z .

При 0 b 2 a функция r = b + 2 a · cos φ неотрицательна для φ ∈ — a r c cos — b 2 a + 2 πk ; arccos — b 2 a + 2 πk , k ∈ Z . Она ограничивает фигуру, которая по конфигурации напоминает кардиоиду.

При b > 2 a функция r = b + 2 a · cos φ является неотрицательной для любого значения угла. Графическая иллюстрация этого случая приведена ниже

Для того, чтобы правильно определить пределы интегрирования, необходимо учитывать соотношение параметров a и b .

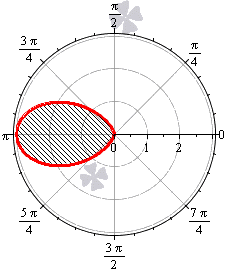
Необходимы вычислить площадь фигуры, которая ограничена линиями, заданными уравнениями r = — 3 + 6 cos φ и r = 5 + 4 cos φ в полярной системе координат.

Решение

Формула r = — 3 + 6 cos φ соответствует фигуре, известной как улитка Паскаля..

Функция r = — 3 + 6 cos φ определена для всех значений угла φ . Нам необходимо выяснить, при каких φ функция будет неотрицательной:

— 3 + 6 cos φ ≥ 0 ⇔ cos φ ≥ 1 2 ⇔ — π 3 + 2 π k ≤ φ ≤ π 3 + 2 πk , k ∈ Z

Проведем вычисление площади фигуры, которая ограничена данной улиткой Паскаля:

S ( G ) = 1 2 ∫ — π 3 π 3 ( — 3 + 6 cos φ ) 2 d φ = 9 2 ∫ — π 3 π 3 ( 1 — 4 cos φ + 4 cos 2 φ ) d φ = = 9 2 ∫ — π 3 π 3 1 — 4 cos φ + 4 · 1 + cos 2 φ 2 d φ = = 9 2 ∫ — π 3 π 3 ( 3 — 4 cos φ + 2 cos ( 2 φ ) ) d φ = 9 2 · 3 φ — 4 sin φ + sin ( 2 φ — π 3 π 3 = = 9 2 · 3 · π 3 — 4 sin π 3 + sin 2 π 3 — 3 · — π 3 — 4 sin — π 3 + sin — 2 π 3 = = 9 2 · 2 π — 3 3

Улитка Паскаля, определяемая формулой r = 5 + 4 cos φ , соответствует пятому пункту. Функция r = 5 + 4 cos φ определена и положительна для всех действительных значений φ . Поэтому, площадь фигуры в этом случае равна:

S ( G ) = 1 2 ∫ 0 2 π ( 5 + 4 cos φ ) 2 d φ = 1 2 ∫ 0 2 π ( 25 + 40 cos φ + 16 cos 2 φ ) d φ = = 1 2 ∫ 0 2 π 25 + 40 cos φ + 16 · 1 + cos ( 2 φ ) 2 d φ = = 1 2 ∫ 0 2 π ( 33 + 40 cos φ + 8 cos ( 2 φ ) ) d φ = 1 2 · 33 φ + 40 sin φ + 4 sin ( 2 φ 0 2 π = = 1 2 · 33 · 2 π + 40 sin ( 2 π + 4 sin ( 4 π ) — 33 · 0 + 40 sin 0 + 4 sin 0 = 33 π

Ответ: S ( G ) = 33 π

Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль

Сразу обратимся к примеру.

Необходимо вычислить площадь фигур в полярной системе координат, первая из которых ограничена первым витком спирали Архимеда r = α φ , α > 0 , а вторая первым витком логарифмической спирали r = α φ , α > 1 .

Решение

Если в задаче сказано, что фигура ограничена первым витком спирали Архимеда, то угол φ изменяется от нуля до двух пи.

Исходя из этого, найдем площадь фигуры по формуле:

S ( G ) = 1 2 ∫ 0 2 π ( α φ ) 2 d ϕ = α 2 2 ∫ 0 2 π φ 2 d φ = α 2 2 · φ 3 3 0 2 π = 4 α 3 π 3 3

Аналогично вычисляется площадь фигуры, ограниченной первым витком логарифмической спирали:

S ( G ) = 1 2 ∫ 0 2 π ( α ϕ ) 2 d ϕ = 1 2 ∫ 0 2 π a 2 φ d φ = 1 4 ln a · a 2 φ 0 2 π = = 1 4 ln a · a 4 π — 1

Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов

Пусть фигура в полярной системе координат ограничена лучами φ = α , φ = β и непрерывными и неотрицательными на интервале φ ∈ α ; β функциями r = p 1 ( φ ) и r = p 2 ( φ ) , причем p 1 ( φ ) ≤ p 2 ( φ ) для любого угла φ = φ 0 ∈ α ; β .

Находим площадь фигуры по формуле S ( G ) = 1 2 ∫ α β p 2 2 ( φ ) — p 1 2 ( φ ) d φ .

Действительно, в силу свойства аддитивности площади, фигуру G можно представить как разность двух криволинейных секторов G 2 и G 1 .

Тогда площадь фигуры G равна разности площадей этих криволинейных секторов:

S ( G ) = S ( G 2 ) — S ( G 1 ) = 1 2 ∫ α β p 2 2 ( φ ) d φ — 1 2 ∫ α β p 1 2 ( φ ) d φ = = 1 2 ∫ α β p 2 2 ( φ ) — p 1 2 ( φ ) d φ

Последний переход возможен в силу третьего свойства определенного интеграла.

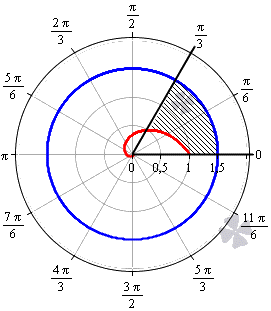
Необходимо вычислить площадь фигуры, которая ограничена линиями φ = 0 , φ = π 3 , r = 3 2 , r = 1 2 φ в полярной системе координат.

Решение

Построим заданную фигуру на графике.

Очевидно, что r = 3 2 больше r = 1 2 φ для любого φ ∈ 0 ; π 3 . Применяем полученную формулу для вычисления площади фигуры:

S ( G ) = 1 2 ∫ 0 π 3 3 2 2 — 1 2 φ 2 d φ = 1 2 ∫ 0 π 3 9 4 — 2 — 2 φ d φ = = 1 2 · 9 4 φ + 1 2 · 2 — 2 φ ln 2 0 π 3 = 1 2 · 9 4 φ + 1 ln 2 · 1 2 2 φ + 1 0 π 3 = = 1 2 · 9 4 · π 3 + 1 ln 2 · 1 2 2 · π 3 + 1 — 9 4 · 0 + 1 ln 2 · 1 2 2 · 0 + 1 = = 1 2 · 3 π 4 + 2 — 2 π 3 — 1 2 · ln 2

Ответ: S ( G ) = 1 2 · 3 π 4 + 2 — 2 π 3 — 1 2 · ln 2

А теперь рассмотрим пример, когда фигура ограничена линиями, заданными в прямоугольной системе координат. Площадь такой фигуры намного проще вычислять, используя полярные координаты.

Необходимо вычислить площадь фигуры, которая ограничена прямыми линиями y = 1 3 x , x = 3 x , окружностями ( x — 2 ) 2 + ( y — 3 ) 2 = 13 , ( x — 4 ) 2 + ( y — 3 ) 2 = 25 .

Решение

В прямоугольной системе координат вычислить площадь полученной фигуры можно, но дело это долгое и хлопотное. Намного проще перейти к полярной системе координат, воспользовавшись формулами перехода.

x = r · cos φ y = r · sin φ ⇒ y = 1 3 x ⇔ r · sin φ = r · cos φ 3 ⇔ t g φ = 1 3 ⇔ φ = π 6 + πk y = 3 x ⇔ r · sinφ = 3 · r · cosφ ⇔ tgφ = 3 ⇔ φ = π 3 + πk ( x — 2 ) 2 + ( y — 3 ) 2 = 13 ⇔ x 2 + y 2 = 4 x + 6 y ⇔ r = 4 cosφ + 6 sinφ ( x — 4 ) 2 + ( y — 3 ) 2 = 25 ⇔ x 2 + y 2 = 8 x + 6 y ⇔ r = 8 cosφ + 6 sinφ

Функция r = 8 cos φ + 6 sin φ больше r = 4 cos φ + 6 sin φ для любого φ ∈ π 6 ; π 3 . Вычисляем площадь фигуры в полярных координатах:

S ( G ) = 1 2 ∫ π 6 π 3 8 cos φ + 6 sin φ 2 — 4 cos φ + 6 sin φ 2 d φ = = 1 2 ∫ π 6 π 3 ( 48 cos 2 φ + 48 cos φ · sin φ ) d φ = = 24 ∫ π 6 π 3 cos 2 φ d φ + 24 ∫ π 6 π 3 cos φ · sin φ d φ = = 12 ∫ π 6 π 3 ( 1 + cos 2 φ ) d φ + 24 ∫ π 6 π 3 sin φ d ( sin φ ) = = 12 · φ + 1 2 sin ( 2 φ ) π 6 π 3 + 12 · sin 2 φ π 6 π 3 = = 12 · π 3 + 1 2 sin 2 π 3 — π 6 + 1 2 sin 2 π 6 + 12 · sin 2 π 3 — sin 2 π 6 = = 12 · π 6 + 12 · 3 2 2 — 1 2 2 = 2 π + 6

Площадь круга: как найти, формулы

О чем эта статья:

площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ

Определение основных понятий

Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.

Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.

Формула вычисления площади круга

Давайте разберем несколько формул расчета площади круга. Поехали!

Площадь круга через радиус

S = π × r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.

Площадь круга через диаметр

S = d 2 : 4 × π, где d — это диаметр.

Площадь круга через длину окружности

S = L 2 : (4 × π), где L — это длина окружности.

Популярные единицы измерения площади:

квадратный миллиметр (мм 2 );
квадратный сантиметр (см 2 );
квадратный дециметр (дм 2 );
квадратный метр (м 2 );
квадратный километр (км 2 );
гектар (га).

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Задачи. Определить площадь круга

Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!

Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.

Диаметр окружности равен двум радиусам.

Используем формулу: S = π × d 2 : 4.

Подставим известные значения: S = 3,14 × 12 2 : 4.

Ответ: 113,04 см 2 .

Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.

Используем формулу: S = π × d 2 : 4.

Подставим известные значения: S = 3,14 × 90 2 : 4.

Ответ: 6358,5 мм 2 .

Задание 3. Найти длину окружности при радиусе 3 см.

Отношение длины окружности к диаметру является постоянным числом.

Получается: L = d × π.

Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.

Подставим значение радиуса: L = 2 × 3,14 × 3.

Ответ: 18,84 см 2 .

Задача: определить площадь круга, если известна длина окружности

Условие задачи:

Длина окружности 5 м. Найти площадь круга, ограниченного этой окружностью.

Дано:
Длина окружности, L = 5 м

Пояснение к рисунку:
O — центр окружности

Найти площадь круга: S

Используем формулу площади круга через радиус. Но нам пока не известен радиус, его надо найти.

Определить радиус, нам поможет формула длины окружности.

После преобразования, выразим радиус через длину окружности и подставим значения.

Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14

Получили значение радиуса окружности.

В формулу площади круга, подставляем найденное значение радиуса.

Ответ:

Если в формулу площади круга подставить выраженный радиус через длину окружности, то получим следующую формулу, в которой площадь круга сразу выражена через длину окружности. Проверим, подставив наше значение

источники:

http://skysmart.ru/articles/mathematic/ploshad-kruga

http://www-formula.ru/zadacha/solve-area-circle-know-length

Источник

Площадь S криволинейного сектора, ограниченного непрерывной кривой r=r(f) и двумя лучами f=f₁ и f=f₂, где f₁<f₂ равняется половине определенного интегралу от квадрата радиуса кривой, проинтегрированного в пределах изменения угла
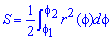
Задачи взяты из программы практикума для студентов мех-мата Львовского национального университета имени Ивана Франко. Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).

Для запоминания основных моментов схема интегрирования и нахождения площадей из примера в пример будет повторяться. Сами ррешеня по возможности будут проиллюстрированы графиками исследуемых кривых.

Найти площади фигур, ограниченных кривыми, заданными в полярных координатах

Пример 2.106 (2418) Вычислить площадь фигуры, ограниченной кривыми r²=a²*cos(2f) (лемниската Бернулли).
Вычисление: Лемниската Бернулли — геометрическое место точек, произведение расстояний от которых до двух фиксированных точек (фокусов) остается постоянным и равняется квадрату половины расстояния между фокусами.
Запишем подинтегральную функцию: r²=a²*cos(2f) (известна за условием).
Найдем пределы интегрирования:
задана кривая замкнутая, симметричная относительно прямых r*cos(f)=0 и r*sin(f)=0.
Наведем график лемнискаты Бернулли

Поскольку заданная функция осями координат делится на четыре равных части и достигает своих критических значений при f₁=0 (r=a) и f₂=p/4 (r=0), то площадь фигуры вычислим для одной части лемнискаты, а результат умножим на 4.
Найдем площадь фигуры интегрированиям по углу

Площадь измеряется в единицах квадратных, однако в этом и следующих примерах размерности наводить не будем, хотя о них помним.

Пример 2.107 (2419) Найти площадь фигуры, ограниченной кривыми r=a* (1+cos(f)) — кардиоида.
Вычисление: Кардиоида — плоская линия, которая описывается фиксированной точкой круга, который катится по неподвижному кругу с таким же радиусом a.
Записываем подинтегральную функцию: r²=a²*(1+cos(f))².
Находим пределы интегрирования: кривая замкнутая, симметричная относительно прямой r*sin(f) =0.
Поскольку заданная функция осями координат делится на две равных части и достигает своих критических значений при f₁=0 (r=2a) и f₂=p (r=0), то площадь фигуры вычислим для половины кардиоиды, а результат умножим на 2.
График кардиоиды имеет вид

Вычислим площадь фигуры, которая ограничена заданной кривой, интегрированием:

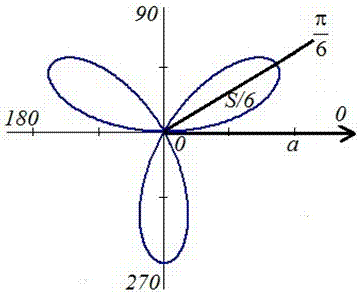
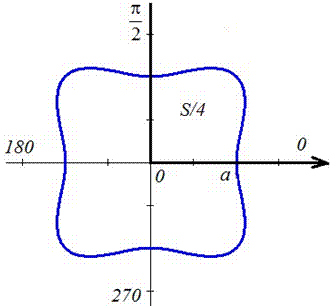
Пример 2.108 (2420) Найти площадь фигуры, ограниченной кривой r=a*sin(f) -трилисник.
Вычисление: Подносим функцию к квадрату, чтобы получить подинтегральную функцию:
r²=a²*sin²(f).
График трилистника в полярной системе координат

Установим пределы интегрирования:
Поскольку заданный график функции делится на шесть равных частей (полупелюсток) и достигает своих критических значений при f₁=0 (r=0) и f₂=p/6 (r=a/2) то площадь фигуры вычислим для одной его части, а результат умножим на 6.
Находим площадь фигуры интегрированием по углу

Получили простую для вычислений формулу площади трилистника S=Pi*a²/4.

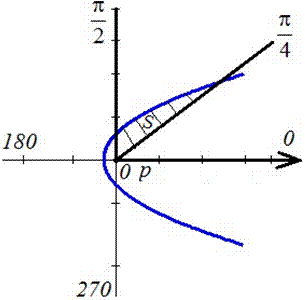
Пример 2.109 ( 2421) Вычислить площадь фигуры, ограниченной кривой 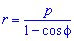(парабола), f₁=p/4, f₂=p/2.
Вычисление: Подносим к квадрату уравнения кривой в полярной системе коринат (СК).

Пределы интегрирования известны f₁=p/4, f₂=p/2 за условием.
График фигуры, площадь которой нужно найти имеет вид

Интегрированием вычисляем площадь фигуры, которая ограничена параболой:

Для вычисления интеграла следует выполнить замену переменных, не забывая при этом , что изменяются пределы интегрирования.

Пример 2.110 ( 2422) Найти площадь фигуры, ограниченной кривой 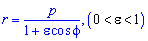(эллипс)
Вычисление: Запишем подинтегральную функцию:

Пределы интегрирования: f₁=0, f₂=2p (начало и конец кривой эллипса).
График эллипса имеет вид

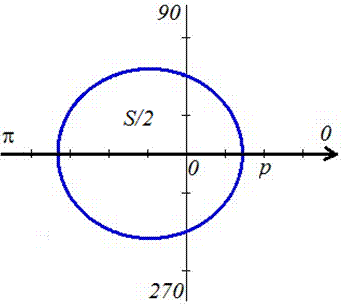
Находим площадь елипса, воспользовавшись следующей формулой интегрирования

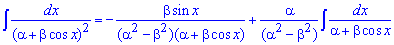
При выведении этой формулы пользовались методом интегрирования частями!

Напоследок превращаем конечную формула с помощью известных формул.
Как видим, ответы задач 2.110 и 2.87 совпадают, то есть площадь эллипса S=Pi*a*b вычислена правильно.

Пример 2.111 (2422.1) Найти площадь фигуры, ограниченной кривой заданной в полярных координатах r=3+2*cos(f).
Вычисление: Сначала находим подинтегральную функцию: r²=(3+2*cos(f))².
Дальше пределы интегрирования: задана кривая замкнутая, симметричная относительно прямой r*sin(f)=0.
Ее график приведен на рисунку ниже

Поскольку задана кривая осями координат делится на две равных части и достигает своих критических значений при углах f₁=0 (r=5) и f₂=p (r=1), то вычислим половину площади фигуры, а результат умножим на 2.
Находим площадь фигуры через определенный интеграл

Интеграл в данном случае не тяжелый и, возведя в квадрат подинтегральную функцию и понизив квадрат косинуса, в результате вычислений получим, что площадь равна S=11*Pi.

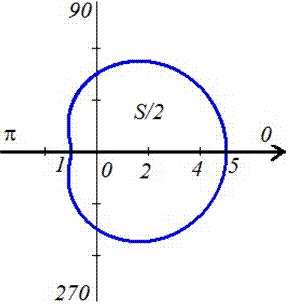
Пример 2.112 (2424.1) Найти площадь фигуры, ограниченной кривой заданной в полярных координатах r²+f²=1.
Вычисление: Выражаемый подинтегральную функцию: r²=1-f² .
Найдем пределы интегрирования.
, поэтому , откуда .

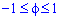
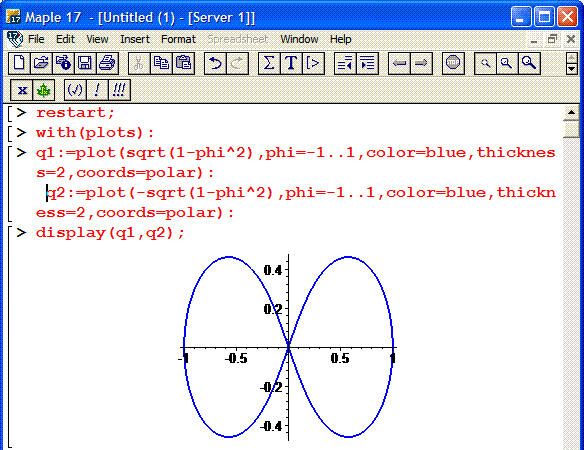
Построим график кривой в математическом пакете Maple17.
Кривая состоит из двух веток корневой функции, поэтому для корректного ее отображения используем следующий код:
> restart;
> with (plots) :
> q1:=plot(sqrt(1-phi^2),phi=-1.1, color=blue, thickness=2, coords=polar):
q2:=plot(-sqrt(1-phi^2),phi=-1.1, color=blue, thickness=2, coords=polar):
> display (q1, q2);
Фрагмент программы Maple приведен ниже

Находим площадь фигуры, которая ограничена кривой:

Интеграл в этом задании простей всех, что рассматривались.

Пример 2.113 ( 2422.2) Вычислить площадь фигуры, ограниченной кривыми .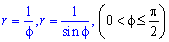
Вычисление: Выписываем подинтегральные функции:

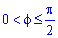
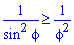
Поскольку на промежутке интегрирования между кривыми выполняется неравенство, то для нахождения площади имеем r₂²-r₁².
Найдем пределы интегрирования: f₁=0 — особенная точка (функция направляется к безграничности) f₁=p/2 (известны за условием).
Находим площадь фигуры через предел от интеграла:

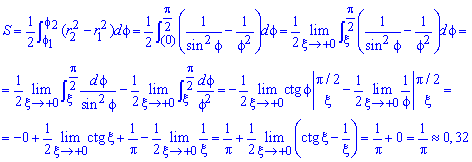
Данный пример хорошо разберите, чтобы не иметь трудностей на экзамене или модуле с подобными.

Пример 2.114 ( 2424) Вычислить площадь фигуры, ограниченной кривой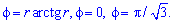
Вычисление: Запишем подинтегральную функцию: r².
Запишем пределы интегрирования:
(известны за условием).
График функций имеет вид

Вычислим площадь фигуры, что приведена на графике.
Для этого сначала находим дифференциал угла f и переходим к интегрированию по радиусу.
Для нахождения интеграла применяем интегрирование частями

Интеграл достаточно трудно находится, поэтому все что содержит формула внимательно проанализируйте.

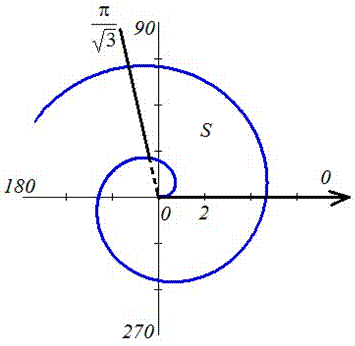
Пример 2.116 (2424.4) Найти площадь фигуры, ограниченной полярными кривыми f=r-sin(r), f=p.
Вычисление: Подинтегральную функция следующая: r².
Пределы интегрирования: f₁=0, (r=0) начало; f₁=p (известно за условием).
График функции имеет вид

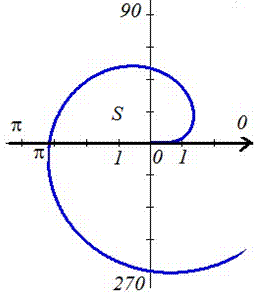
Находим площадь фигуры, применяя дважды интегрирование частями

Интеграл не слишком сложен, все переходы просьба проанализировать самостоятельно.

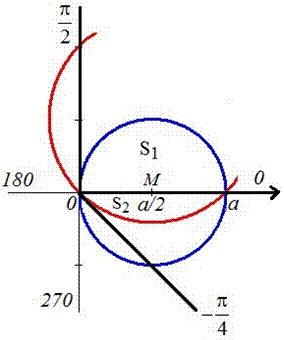
Пример 2423 Вычислить площадь фигуры, ограниченной полярными кривыми r=a*cos(f), r=a(cos(f)+sin(f)), M (a/2;0)єS.
Вычисление: Для представления фигуры, площадь которой нужно найти предварительно выполняем построение графика заданных функций

Поскольку точка M (a/2;0)єS делит искомую площадь на две части, то имеем два интеграла

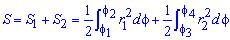
Записываем уравнение подинтегральных функций:

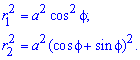
Определяем пределы интегрирования:
, где и где (точки пересечения линий).
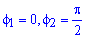
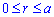
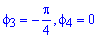
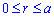
Вычисляем площадь изображенной фигуры интегрированием

Здесь воспользовались известные тригонометрические формулы для понижения степени косинусов и синусов под интегралом. Все остальное сводятся к применению простых формул интегрирования, и нахождения их значений.

Пример 2424.2 Найти площадь фигуры, ограниченной полярными кривыми f=sin(p*r), r пренадлежит [0;1].
Вычисление: Запишем подинтегральную функцию: r².
Запишем пределы интегрирования: При росте r от 0 к 1/2 угол f растет от 0 к 1, при росте r от 1/2 к 1 угол f спадает от 1 к 0, поэтому величина интеграла в пределах r пренадлежит [0;1] имеет знак «минус».

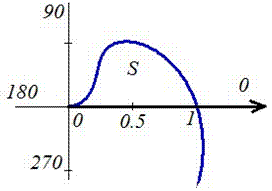
Находим площадь фигуры, предварительно перейдя к новой переменной под интегралом:

Перед интегралом (после замены переменных) поставили знак «минус», поскольку интеграл является отрицательным на этом промежутке, а площадь должна быть положительной.

Перейти к полярным координатам и найти площади фигур, ограниченных кривыми

Пример 2426 Перейти к полярным координатам и найти площадь фигуры x³+y³=3a*x*y (лист Декарта)
Вычисление: Перейдем от прямоугольной системы координат к полярной системе координат за формулами перехода:

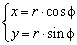
При подстановке в уравнение получим

Поднесем к квадрату, чтобы получить подинтегральную функцию:

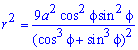
Выпишем пределы интегрирования:
, потому что при и при .
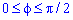
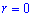
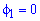
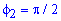
График функции имеет вид

Найдем площадь фигуры интегрированиям:

Для получения конечной формулы площади дважды применяли замену переменных под интегралом.
Внимательно разберите, как при этом изменяются пределы и эффективность методики.

Пример 2427 Перейти к полярным координатам и найти площадь фигуры x⁴+y⁴=3a²(x²+y²)
Вычисление: Переходим от прямоугольной к полярной системе координат:

Выражаемый подинтегральную функцию делением:

Запишем пределы интегрирования:
(функция парная).
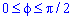
Ее график изображен на рисунку

Оси прямоугольной системы координат являются осями симметрии для фигуры, которая ограничена заданной линией, поэтому площадь найдем для симметричной части и результат умножим на 4.
Находим площадь фигуры через интеграл:

Пример 2428 Перейти к полярным координатам и найти площадь фигуры (x²+y²)²=2a²*x*y (лемниската).
Вычисление: Выполняем переход от прямоугольной к полярной системе координат:

— подинтегральная функция.
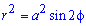
График исследуемой кривой следующий

Запишем пределы интегрирования: учитывая симметрию точек лемнискаты относительно прямой r*sin(f) =r*cos (f) и относительно начала координат, то площадь фигуры будем искать в пределах 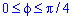и результат умножим на 4 (смотри пример 2.106).
Находим площадь фигуры интегрированием:

Вычислений в этом задании минимум.
В следующих публикациях Вы найдете больше примеров на применение определенного интеграла при вычислении длины дуги, объемов фигур вращения и площадей поверхностей.

Источник

Площадь
фигуры, ограниченной графиком непрерывной
функции

=
,
(
0),
двумя прямыми

и осью OX
, или площадь криво-линейной трапеции,
ограниченной дугой графика функции

в (рис.1), вычисляется по формуле :

(1)

рис
1.

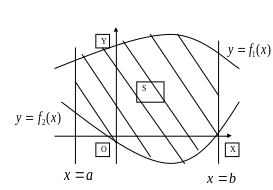
Площадь
фигуры , ограниченной графиками
непрерывных функции

и двумя прямыми

(рис.2), определяется по формуле :

(2)

рис.
2

Пример1.
Найти площадь фигуры, лежащей в правой
полуплоскости и ограниченной окружностью

и параболой

Решение:

найдем
точки пересечения кривых ( рис.3), решив
систему уравнений :

рис.
3

Используя
симметрию относительно оси OX
, найдем искомую площадь как удвоенную
сумму площадей криволинейных трапеций
,ограниченных соответственно дугами
параболы

,
0x2
и окружностью.

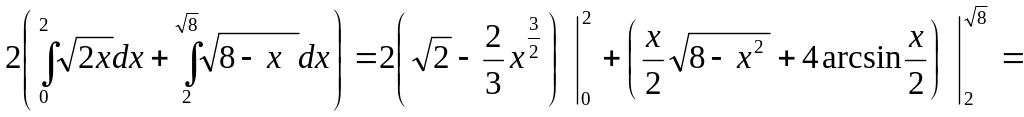
Иногда
удобно использовать формулы , аналогичные
(1) и (2) , но по переменной

(считая x
функцией от

),
в частности

(3)

Если
фигура ограничена кривой, имеющей
параметрические уравнения

=

,

,
прямыми

и осью OX,
то площадь вычисляется по формуле :

(4),

где
пределы интегрирование находятся из
уравнений

на
отрезке

.

Формула
(4) применима также для вычисления площади
фигуры, ограниченной замкнутой кривой
( изменения параметра t
от

до

должно
соответствовать обходу контура по
часовой стрелке).

Пример2.
Найти площадь петли кривой

Решение:
Найдем точки пересечения кривой с
координатами осями. Имеем : x=0
при t=
;
y=0
при t=0,
t=
.Следовательно,
получаем следующие точки:

при
t=1;

при t=-1;

при
t=0;

при t=
.

Точка

является точкой самопересечения кривой.
При

При

(рис.4).

График
функции

;

,

при

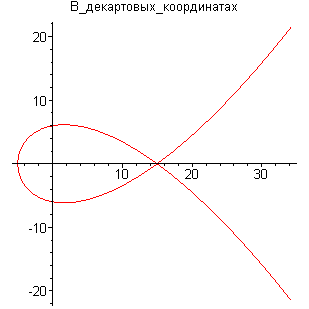
Площадь фигуры
находим как удвоенную площадь верхней
ее половины:

Площадь
фигуры, ограниченной графиком непрерывной
функции

и двумя лучами

где

— полярные координаты, или площадь
криволинейного сектора , ограниченного
дугой графика функции

,

,
вычисляется по формуле:

(5).

Пример
3. Найти площадь лунки , ограниченной
дугами окружностей

Окружности пересекаются при

;
рассматриваемая фигура ( рис.5) симметрична
относительно луча

График
функции

;

,

при

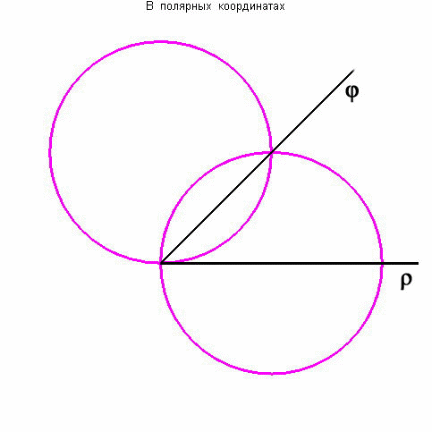
Следовательно,
ее площадь можно вычислять так:

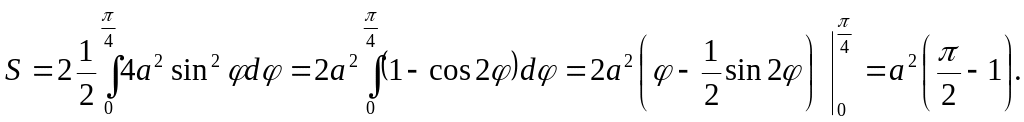
ВАРИАНТЫ

Вычислить
площадь фигуры, ограниченной данными
линиями:

В-1.

и
ее асимптотой.
Кардиоидой

.
.

В-5.

и
касательные к ней , проведенные через
токи
одной
аркой циклиды

В-3.

касательной
к ней в точке

и осью OX.
Астроидой
(
Бернулли ) .

В-4.

,
касательной к ней в точке x=e
и осью OX.
Петли
линии

.
(
улитка Паскаля )

В-5.

,
касательной к ней в точке

.
Одной
арки циклоиды

и OX.
.

В-6.

касательной
к ней в точке

и x=1.
Петли
линии
(кардиоида)

В-7.

касательной
к ней в точке M

к осью ординат.
Петли
кривой
(
лепестковая роза).

В-8.

Параболой

и гиперболой
(в
не круга

)

В-9

Найдите
площадь фигуры, ограниченной графиком
функции

и касательными к этому графику,
проведенными через точку

.

В-10

Найдите
площадь фигуры, ограниченной графиком
функции

и касательными к этому графику,
проведенными через точку

.

В-11

Найдите
площадь фигуры, ограниченной графиками
функций

,

и осью ординат.

В-12

В-13

В-14

В-15

В-16

В-17

В-18

В-19

В-20

площадь,
ограниченную кардиоидой

и окружностью

.

В-21

В-22

одной
петлей кривой

(общая область)

В-23

В-24

В-25

Вычислить
площадь, ограниченную параболой

и осью абсцисс.

Вопросы к
лабораторной работе №9:

Какая
фигура называется квадрируемой? Какие
вы знаете условия квадрируемости?
Какими свойствами
обладает квадрируемая фигура?
Как
вычисляется площадь плоской фигуры,
ограниченной прямыми

и непрерывными кривыми

и

,
при условии, что

для

?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Задачка это школьная, но, несмотря на то, почти 100% встретится в вашем курсе высшей математики. Поэтому со всей серьёзностью отнесёмся ко ВСЕМ примерам, и первое, что нужно сделать – это ознакомиться с Приложением Графики функций, чтобы освежить в памяти технику построения элементарных графиков. …Есть? Отлично! Типовая формулировка задания звучит так:

Пример 10
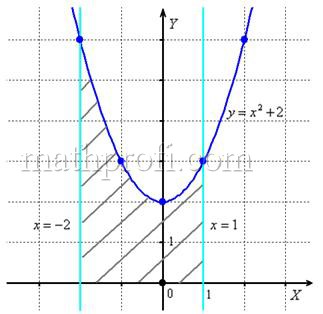
Вычислить площадь фигуры, ограниченной линиями .

И первый важнейший этап решения состоит как раз в построении чертежа. При этом я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций.

В нашей задаче: прямая определяет ось , прямые параллельны оси и парабола симметрична относительно оси , для неё находим несколько опорных точек:

Искомую фигуру желательно штриховать:

Второй этап состоит в том, чтобы правильно составить и правильно вычислить определённый интеграл. На отрезке график функции расположен над осью , поэтому искомая площадь:

Ответ:

После того, как задание выполнено, полезно взглянуть на чертёж
и прикинуть, реалистичный ли получился ответ.

И мы «на глазок» подсчитываем количество заштрихованных клеточек – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получилось, скажем, 20 квадратных единиц, то, очевидно, где-то допущена ошибка – в построенную фигуру 20 клеток явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.

Пример 11
Вычислить площадь фигуры, ограниченной линиями и осью

Быстренько разминаемся (обязательно!) и рассматриваем «зеркальную» ситуацию – когда криволинейная трапеция расположена под осью :

Пример 12
Вычислить площадь фигуры, ограниченной линиями , и координатными осями.

Решение: найдём несколько опорных точек для построения экспоненты:

и выполним чертёж, получая фигуру площадью около двух клеток:

Если криволинейная трапеция расположена не выше оси , то её площадь можно найти по формуле: .
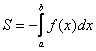
В данном случае:

Ответ: – ну что же, очень и очень похоже на правду.

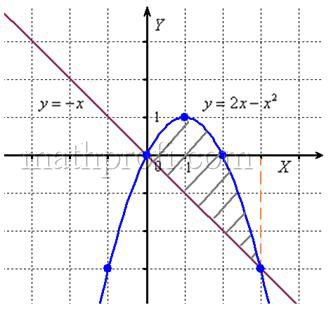
На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому от простейших школьных задачек мы переходим к более содержательным примерам:

Пример 13
Найти площадь плоской фигуры, ограниченной линиями , .

Решение: сначала нужно выполнить чертеж, при этом нас особо интересуют точки пересечения параболы и прямой , поскольку здесь будут находиться пределы интегрирования. Найти их можно двумя способами. Первый способ – аналитический. Составим и решим уравнение:

таким образом:

Достоинство аналитического способа состоит в его точности, а недостаток – в длительности (и в этом примере нам ещё повезло). Поэтому во многих задачах бывает выгоднее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой».

С прямой всё понятно, а вот для построения параболы удобно найти её вершину, для этого возьмём производную и приравняем её к нулю:
– именно в этой точке и будет находиться вершина. И, в силу симметрии параболы, остальные опорные точки найдём по принципу «влево-вправо»:

Выполним чертеж:

А теперь рабочая формула: если на отрезке некоторая непрерывная функция больше либо равна непрерывной функции , то площадь фигуры, ограниченной графиками этих функций и отрезками прямых , можно найти по формуле:

Здесь уже не надо думать, где расположена фигура – над осью или под осью, а, грубо говоря, важно, какой из двух графиков ВЫШЕ.

В нашем примере очевидно, что на отрезке парабола располагается выше прямой, а поэтому из нужно вычесть

Завершение решения может выглядеть так:

На отрезке : , по соответствующей формуле:

Ответ:

Следует отметить, что простые формулы, рассмотренные в начале параграфа – это частные случаи формулы 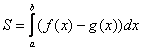. Поскольку ось задаётся уравнением , то одна из функций будет нулевой, и в зависимости от того, выше или ниже лежит криволинейная трапеция, мы получим формулу либо

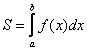
А сейчас пара типовых задач для самостоятельного решения

Пример 14
Найти площадь фигур, ограниченных линиями:

а) , .

б) , ,

Решение с чертежами и краткими комментариями в конце книги

В ходе решения рассматриваемой задачи иногда случается забавный казус. Чертеж выполнен правильно, интеграл решён правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз ошибался ваш покорный слуга. Вот реальный случай из жизни:

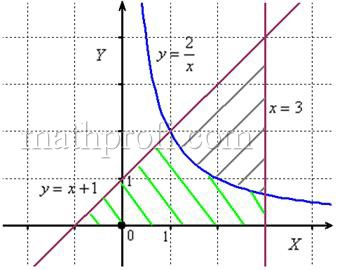
Пример 15
Вычислить площадь фигуры, ограниченной линиями

Решение: выполним бесхитростный чертёж,

хитрость которого состоит в том, что искомая площадь заштрихована зелёным цветом (внимательно смотрИте на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована серым цветом! Особое коварство состоит в том, что прямую можно недочертить до оси , и тогда мы вовсе не увидим нужную фигуру.

Этот пример ещё и полезен тем, что в нём площадь фигуры считается с помощью двух определённых интегралов. Действительно:

1) на отрезке над осью расположен график прямой ;
2) на отрезке над осью расположен график гиперболы .

Совершенно понятно, что площади можно (и нужно) сложить:

Ответ:

И познавательный пример для самостоятельного решения:

Пример 16
Вычислить площадь фигуры, ограниченной линиями , , и координатными осями.

Итак, систематизируем важные моменты этой задачи:

На первом шаге ВНИМАТЕЛЬНО изучаем условие – КАКИЕ функции нам даны? Ошибки бывают даже здесь, в частности, арккотангенс зачастую принимают за арктангенс. Это, кстати, относится и к другим заданием, где встречается арккотангенс.

Далее следует ПРАВИЛЬНО выполнить чертёж. Сначала лучше построить прямые (если они есть), затем графики других функций (если они есть J). Последние во многих случаях выгоднее строить поточечно – найти несколько опорных точек и аккуратно соединить их линией.

Но здесь могут подстерегать следующие трудности. Во-первых, из чертежа не всегда понятны пределы интегрирования – так бывает, когда они дробные. На mathprofi.ru в соответствующей статье я рассмотрел пример с параболой и прямой , где из чертежа не понятна одна из точек их пересечения. В таких случаях следует использовать аналитический метод, составляем уравнение:

и находим его корни:
– нижний предел интегрирования, – верхний предел.

Во-вторых, не всегда понятен «внешний вид» линии, и функция (Пример 16) – яркий тому пример. Я и сам «с ходу» не представляю, как выглядит график этой функции. Здесь можно воспользоваться специализированными программами или онлайн сервисами (а-ля «построить график онлайн»), а в экстремальной ситуации найти побольше опорных точек (штук 10-15), чтобы поточнее провести «неизвестную» кривую.
Ну и, конечно, я призываю вас повышать свои знания и навыки в графиках, в частности, приведу прямую ссылку на особо полезную статью:
http://mathprofi.ru/kak_postroit_grafik_funkcii_s_pomoshyu_preobrazovanii.html

После того, как чертёж построен, анализируем полученную фигуру – ещё раз окидываем взглядом предложенные функции и перепроверяем, ТА ЛИ это фигура. Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части.

Составляем определённый интеграл или несколько интегралов по формуле 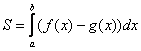, все основные вариации мы разобрали выше.

Решаем определённый интеграл (ы). При этом он может оказаться достаточно сложным, и тогда применяем поэтапный алгоритм: 1) находим первообразную и проверяем её дифференцированием, 2) используем формулу Ньютона-Лейбница.

Результат полезно проверить с помощью программного обеспечения / онлайн сервисов или просто «прикинуть» по чертежу по клеточкам. Но и то, и другое не всегда осуществимо, поэтому крайне внимательно относимся к каждому этапу решения!

1.9. Объём тела вращения

1.7. Геометрический смысл определённого интеграла

| Оглавление |

Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник