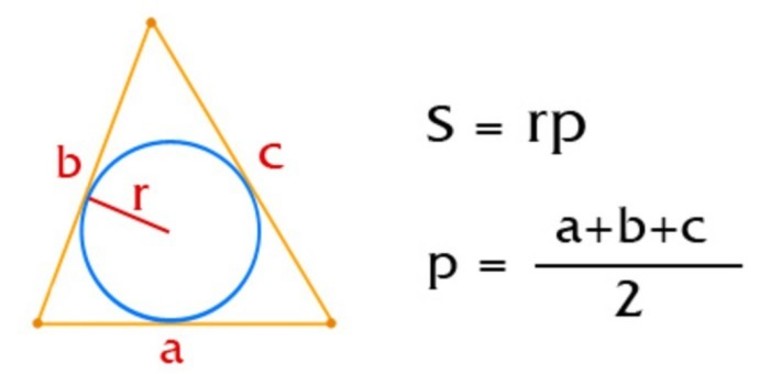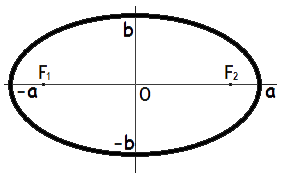Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Содержание
- Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
- Формула нахождения площади круга через радиус:
- Формула нахождения S-площади круга через D-диаметр:
- Нахождение S круга, если известна длина окружности:
- Площадь круга, вписанного в квадрат: формула, примеры решения задач
- Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
- Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
- Площадь круга, описанного около квадрата: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
- Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
- Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
- Видео: Математика | Вычисление площадей круга и его частей
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:
Примеры решения заданий по нахождению S-площади круга через R-радиус:
————————————————————————————————————————
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:
Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Площадь круга, вписанного в квадрат: формула, примеры решения задач
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
Решайте так: Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
Площадь круга, описанного около квадрата: формула, примеры решения задач
Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
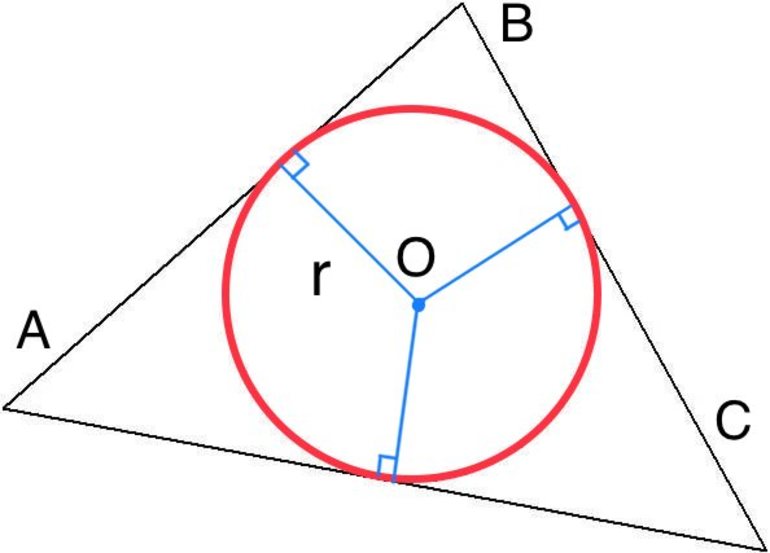
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Задача №3
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
Площадь треугольника через радиус описанной окружности
Как найти площадь треугольника через радиус описанной окружности?
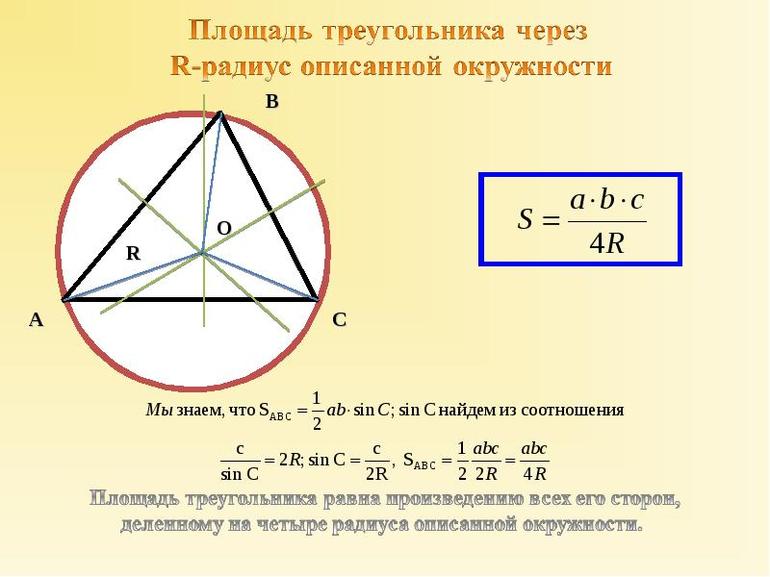
Площадь треугольника равна частному от деления произведения сторон треугольника на четыре радиуса описанной около треугольника окружности.
Формула для нахождения площади треугольника через радиус описанной окружности:
окружность (O; R) — описанная,
Выразим из этой формулы синус альфа
и подставим полученное выражение в первую формулу
Площадь треугольника через радиус описанной окружности — формулы и примеры определения
Фигура с тремя сторонами
Чтобы понять, как рассчитывать площадь треугольника, вписанного в окружность, необходимо иметь четкое представление о рассматриваемой фигуре. Каждый школьник знает о геометрическом объекте, который ограничен тремя отрезками. Основными элементами треугольника являются следующие:
- Стороны, которых у фигуры три. Они могут быть равны по длине или отличаться друг от друга. При этом всегда справедливым остается тот факт, что длина любой стороны меньше суммы длин двух других.
- Вершины — это три точки, которые образованы на пересечении соответствующих сторон. Каждая из них характеризуется определенным значением угла. Для трех углов треугольника справедливо следующее равенство: ∠A + ∠B + ∠C = 180 °, где латинскими буквами названы соответствующие вершины.
Помимо вершин и сторон, треугольник характеризуется дополнительными отрезками, которые часто используются для доказательства теорем и решения геометрических задач. К имеющим специальное название отрезкам относятся такие:
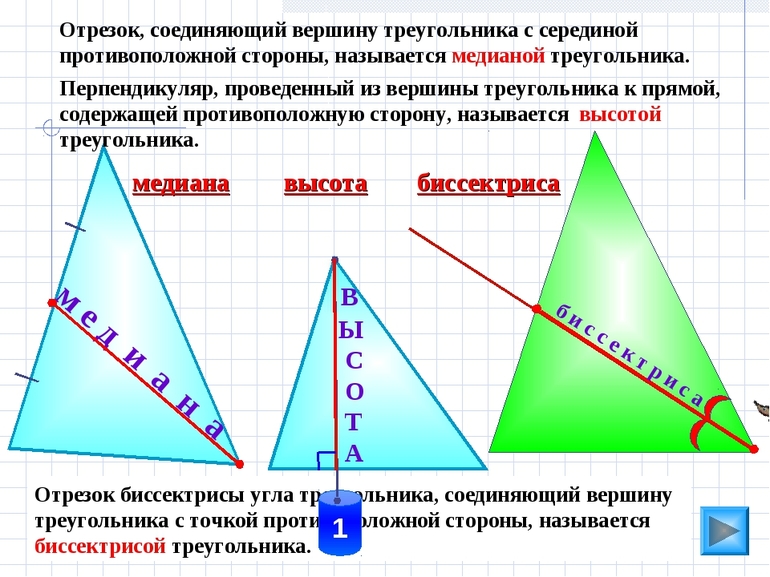
- Медиана — делящий треугольник на две фигуры с одинаковой площадью отрезок. Он проходит через вершину и середину противоположной стороны. Все три медианы пересекаются в одной точке, которая является массовым центром рассматриваемого геометрического объекта.
- Биссектриса — отрезок, который делит пополам угол при вершине. Все три биссектрисы, как и медианы, пересекаются в одной точке, которая является центром вписанной в треугольник окружности.
- Высота — перпендикуляр, который через вершину опускается на противоположную сторону. Высоты часто используются при вычислении площадей.
- Средняя линия — проходящая через середины двух сторон линия, которая является параллельной третьей. Обе стороны отсекают отрезок, длина которого составляет половину от длины противоположной стороны.
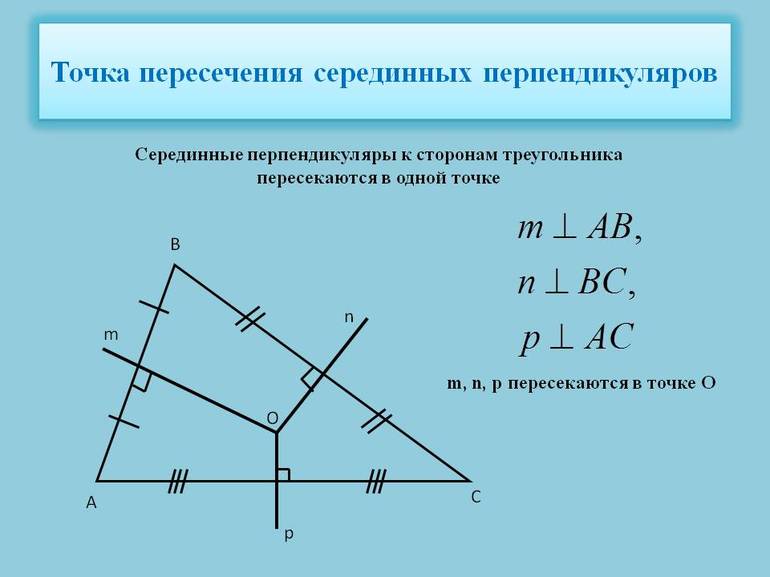
- Медиатриса или серединный перпендикуляр — это прямая линия, которая пересекает под углом 90 ° сторону треугольника. Важным свойством медиатрис является тот факт, что точка из пересечения — это центр описанной вокруг фигуры окружности.
Вписанный в окружность треугольник
Чтобы уметь вычислять площадь описанного треугольника, следует понимать, о каком взаимном расположении многоугольника и окружности идет речь. Согласно определению, если через все вершины полигона проходит окружность, значит, он считается вписанным в нее. Это простое определение не всегда выполняется для произвольного многоугольника, однако, для любой правильной фигуры оно будет справедливым, например, для квадрата или прямоугольника.
Касательно треугольника следует отметить, что он является единственным многоугольником, для которого всегда можно найти центр и радиус описывающей его окружности. Причем независимо от того, какой тип фигуры рассматривается.
Пересечение медиатрис
В рассматриваемой фигуре имеется три разных медиатрисы. Каждую из них построить несложно для любой из сторон. Для построения следует выполнить последовательность действий:
- Выбрать сторону.
- Установить циркуль в один из концов стороны и провести дугу окружности, которая будет пересекать сторону дальше, чем посередине.
- Пункт 2 выполнить, установив циркуль во второй конец стороны.
- Соединить точки пересечения дуг в одну линию. Она является медиатрисой.
Из проделанных построений следует один важный факт для всех треугольников: точка пересечения их медиатрис является центром описывающей фигуру окружности. Доказать это утверждение легко. Например, имеется треугольник ABC. Пусть проведена медиатриса m к стороне AB. Любая из точек, принадлежащих прямой m, находится на одинаковом расстоянии от вершин A и B.
Пусть проведена еще одна медиатриса n к стороне BC. Прямые m и n пересекаются в точке O. Поскольку O принадлежит обеим медиатрисам, то она, с одной стороны, находится на одном расстоянии от A и B, с другой стороны, она находится на одинаковой дистанции от вершин B и C. Этот факт дает право сделать вывод о том, что расстояния OA, OB и OC равны. Если их обозначить буквой R, то можно говорить, что R — радиус окружности с центром в точке O, которая проходит через три вершины треугольника, то есть описывается его.
Очевидно, что третья медиатриса также пройдет через O. В противном случае будут существовать три разные точки, которые одновременно будут находиться на одинаковом расстоянии от трех вершин треугольника и будут лежать в одной плоскости с ним, а это невозможно из свойств двумерного пространства.
Типы фигур и точка O
Поскольку для треугольника любого типа можно провести описывающую его окружность, то представляет интерес рассмотреть вопрос положения ее центра O. В общем случае существуют три типа рассматриваемого многоугольника:
- С острыми углами, то есть все они менее 90 °. К этим треугольникам относятся равносторонние. Для них центр описанной окружности всегда расположен внутри фигуры.
- С одним тупым углом и двумя острыми. Это может быть либо равнобедренный треугольник, либо фигура общего типа. Для нее точка O всегда расположена вне области, ограниченной сторонами многоугольника, то есть за его пределами.
- Прямоугольный. Для такого типа треугольников центр описанной окружности расположен точно посередине гипотенузы. Это свойство треугольника, которое доказывается просто, если рассмотреть точку пересечения двух средних линий, проведенных относительно катетов. Поскольку O лежит посередине гипотенузы, то последняя является диаметром описанной окружности. Любой треугольник, который опирается на диаметр одной из своих сторон, и третья вершина которого лежит на окружности, является прямоугольным.
Очевидно, что если треугольник является полностью вырожденным, то провести описывающую его окружность нельзя, поскольку такая фигура обращается в прямой отрезок.
Формулы для определения площади
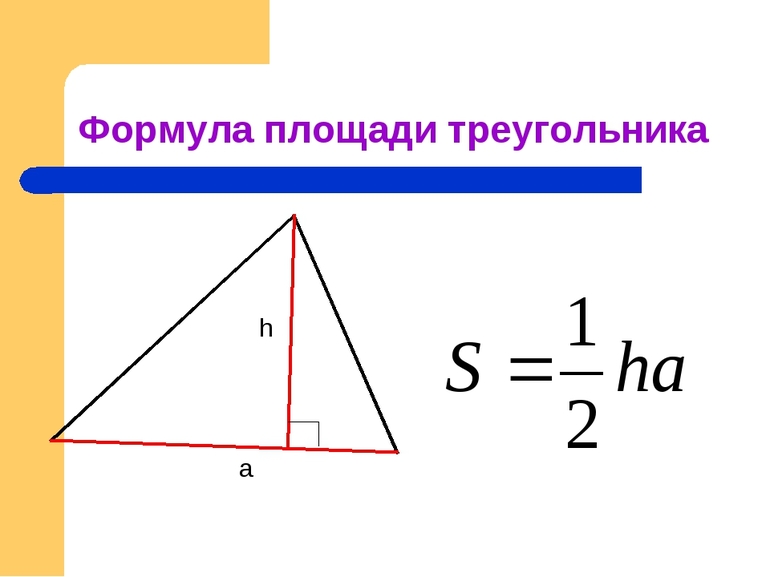
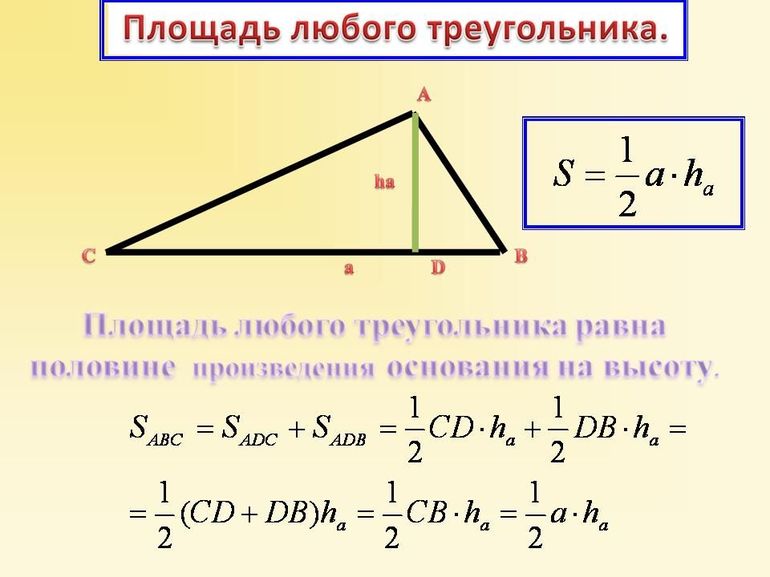
Как известно, площадь треугольника произвольного типа может быть рассчитана, как половина произведения высоты h на длину основания a: S = ½*h*a. Существует также еще одно универсальное выражение для определения S — это половина модуля векторного произведения направляющих отрезков, образующих любые две стороны.
Что касается формул площади треугольника, описанного около окружности, то нужно отметить, что известны несколько из них. Соответствующие равенства имеют следующий вид:
Где a, b, c — длины соответствующих сторон треугольника, ha, hb, hc — высоты, проведенные к a, b и c, соответственно. Видно, что все три формулы требуют знание минимум 4 параметров для рассматриваемой фигуры (радиус и три высоты или три длины сторон).
Полезно также привести формулу для расчета радиуса R:
Здесь p = (a+b+c)/2 — полупериметр треугольника. Следует отметить, что знаменатель в выражении для радиуса является не чем иным, как формулой Герона для расчета площади S фигуры.
Решение задач
Как правило, прямое использование формул площади треугольника через окружность описанную является невозможным для типичных геометрических задач. Для их решения необходимо внимательно проанализировать условие и использовать все имеющиеся знания для определения неизвестных в выражениях для S через R.
Для некоторых задач может потребоваться использование уравнений прямых, которые на плоскости в векторной форме имеют вид:
(x, y) = (x0, y0) + α*(v1, v2).
Здесь (x, y) и (x0, y0) — координаты произвольной и известной точек прямой, соответственно, (v1, v2) — координаты направляющего вектора, α — числовой параметр.
Для закрепления полученных знаний полезно решить одну простую задачу. Известно, что один из острых углов в прямоугольном треугольнике составляет 30 °. Чему равна площадь этой фигуры, если радиус описанной окружности для нее составляет 12 см.
Для решения задачи воспользуемся следующим выражением через радиус окружности, описанной около треугольника, для площади:
Пусть c — это гипотенуза, тогда c = 2*R = 24 см. Катеты a и b можно связать с гипотенузой функциями синуса и косинуса:
- a = c*cos (α) = 24*3 0,5 /2 = 20,7846 см;
- b = c*sin (α) = 24*½ = 12 см.
Подставляя полученные значения в формулу для S через R, можно получить ответ:
S = a*b*c/(4*R) = 20,7846*12*24/(4*12) ≈ 124,71 см 2 .
Важно понимать, что формулы расчета площади рассматриваемого многоугольника через радиус описанной окружности используются редко, поскольку они могут быть заменены аналогичными более простыми выражениями, как в случае с высотой и основанием. В решенной задаче, например, можно было не применять указанную для S формулу, а просто рассчитать полупроизведение катетов:
S = ½*a*b = ½*20,7846*12 ≈ 124,71 см 2 .
Таким образом, вокруг каждого треугольника можно описать окружность радиуса R, центр которой расположен в точке пересечения его серединных перпендикуляров (медиатрис). Существует несколько формул для вычисления площади фигуры через радиус R, однако, все они требуют знания либо сторон, либо высот треугольника, и в большинстве случаев могут быть заменены более простыми выражениями при решении задач.
Как найти площадь треугольника
О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
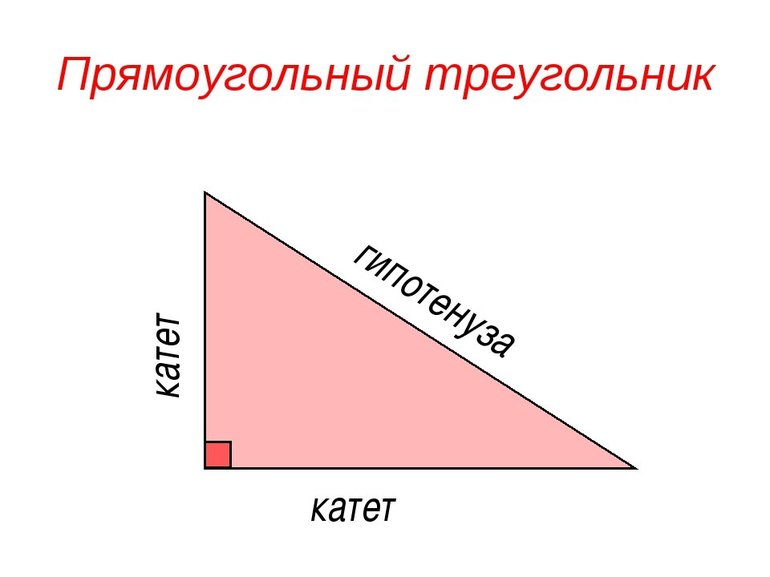
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
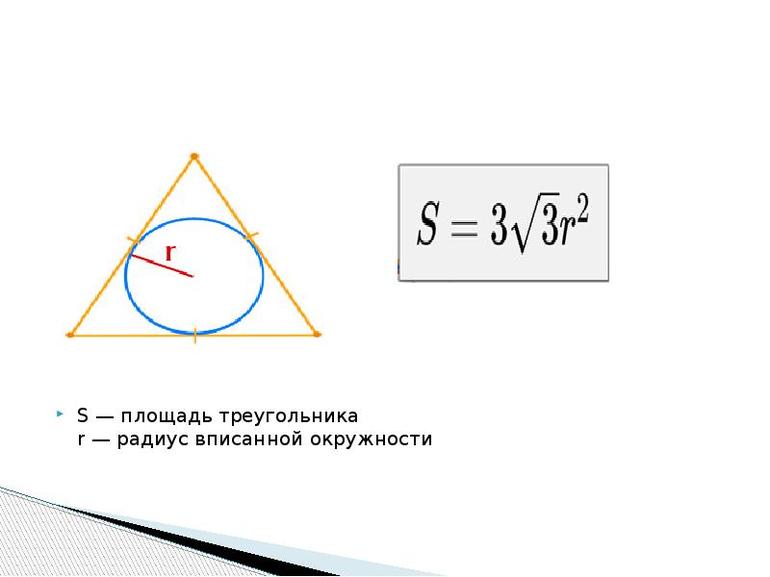
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
http://nauka.club/matematika/geometriya/ploshchad-treugolnika-cherez-radius.html
http://skysmart.ru/articles/mathematic/ploshad-treugolnika
Формулы площади геометрических фигур
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
-
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты -
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
-
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. -
Формула площади треугольника по трем сторонам и радиусу описанной окружности
-
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.где S — площадь треугольника,
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b,
r — радиус вписанной окружности,
R — радиус описанной окружности,p = a + b + c — полупериметр треугольника. 2
Формулы площади квадрата
-
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
-
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.где S — площадь квадрата,
a — длина стороны квадрата,
d — длина диагонали квадрата.
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
где S — Площадь прямоугольника,
a, b — длины сторон прямоугольника.
Формулы площади параллелограмма
-
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = a · b · sin α
-
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.где S — Площадь параллелограмма,
a, b — длины сторон параллелограмма,
h — длина высоты параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма.
Формулы площади ромба
-
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
-
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.где S — Площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба,
α — угол между сторонами ромба,
d1, d2 — длины диагоналей.
Формулы площади трапеции
-
Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a — b| -
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высотугде S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,p = a + b + c + d — полупериметр трапеции. 2
Формулы площади выпуклого четырехугольника
-
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S — площадь четырехугольника,
d1, d2 — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника. -
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
-
Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2θ
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d2 — полупериметр четырехугольника,
θ = α + β2 — полусумма двух противоположных углов четырехугольника.
-
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p — a)(p — b)(p — c)(p — d)
Формулы площади круга
-
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
-
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.где S — Площадь круга,
r — длина радиуса круга,
d — длина диаметра круга.
Формулы площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
S = π · a · b
где S — Площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.

-
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне
высоты -
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
-
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между
ними. - Формула площади треугольника по трем сторонам и радиусу описанной окружности
-
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.где S — площадь треугольника,
a, b, c — длины сторон
треугольника,
h — высота треугольника,
γ — угол между сторонами a и b,
r — радиус вписанной окружности,
R — радиус описанной окружности,p = a + b + c — полупериметр треугольника. 2

-
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
-
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.где S — Площадь квадрата,
a — длина стороны квадрата,
d — длина диагонали квадрата.

Площадь
прямоугольника равна произведению длин
двух его смежных сторон
S = a · b
где S — Площадь
прямоугольника,
a,
b —
длины сторон прямоугольника.

-
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = a · b · sin α
-
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.где S — Площадь параллелограмма,
a, b — длины сторон параллелограмма,
h — длина высоты параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма.

-
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
-
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
где S — Площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба,
α — угол между сторонами ромба,
d1, d2 — длины диагоналей.

-
Формула Герона для трапеции
S = a + b √(p — a)(p — b)(p — a — c)(p — a — d) 4|a — b| -
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высотугде S — Площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,p = a + b + c + d — полупериметр трапеции. 2
-
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S — площадь четырехугольника,
d1, d2 — длины диагоналей четырехугольника,
α — угол между
диагоналями четырехугольника. -
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружностиS = p · r
-
Формула площади четырехугольника по длине сторон и значению противоположных угловS = √(p — a)(p — b)(p — c)(p — d) — abcd cos2θ
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,p = a + b + c + d — полупериметр четырехугольника, 2 θ = α + β — полусумма двух противоположных углов четырехугольника. 2 -
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p — a)(p — b)(p — c)(p — d)

-
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
-
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.где S — Площадь круга,
r — длина радиуса круга,
d — длина диаметра круга.

Площадь
эллипса равна произведению длин
большой и малой полуосей эллипса на число пи.
S = π · a · b
где S — Площадь
эллипса,
a — длина большей полуоси
эллипса,
b — длина меньшей полуоси
эллипса.
Площади фигур. Основные формулы.
Площадь треугольника.
| Формула | Рисунок | Расшифровка формулы |
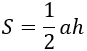 |
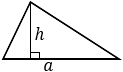 |
а — основание, h — высота, проведенная к этому основанию. Формула применима для любого треугольника. |
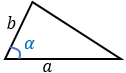 |
a, b — стороны, α — угол между этими сторонами. Формула применима для любого треугольника. |
|
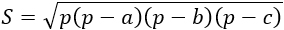 |
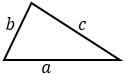 |
a, b, с — стороны, р — полупериметр (сумма трех сторон, деленная пополам). Формула применима для любого треугольника. |
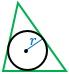 |
r — радиус вписанной в треугольник окружности, р — полупериметр (сумма трех сторон, деленная пополам). Формула применима для любого треугольника. |
|
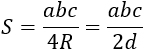 |
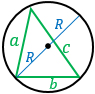 |
a, b, с — стороны, R — радиус описанной около треугольника окружности, d — диаметр описанной окружности. Формула применима для любого треугольника. |
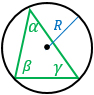 |
R — радиус описанной около треугольника окружности, α, β, γ — углы треугольника. Формула применима для любого треугольника. |
|
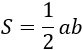 |
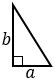 |
a, b — катеты. Формула применима для прямоугольного треугольника. |
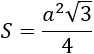 |
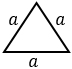 |
a — сторона. Формула применима для равностороннего (правильного) треугольника. |
Площадь квадрата и прямоугольника.
Площадь параллелограмма и ромба.
| Формула | Рисунок | Расшифровка формулы |
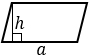 |
а — одна из сторон параллелограмма, h — высота, проведенная к этой стороне | |
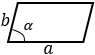 |
а, b — стороны параллелограмма, α — угол между этими сторонами | |
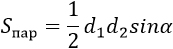 |
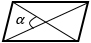 |
d1, d2 — диагонали, α — угол между диагоналями (можно брать любой угол, т.к. синусы смежных углов равны) |
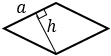 |
а — сторона ромба, h — высота, проведенная к этой стороне | |
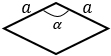 |
а — сторона ромба, α — угол между этими сторонами | |
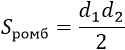 |
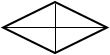 |
d1, d2 — диагонали ромба |
Площадь трапеции.
| Формула | Рисунок | Расшифровка формулы |
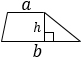 |
а, b — основания трапеции, h — высота. Формула применима для любой* трапеции. |
|
|
m — средняя линия трапеции, h — высота. Формула применима для любой трапеции. |
||
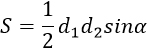 |
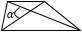 |
d1, d2 — диагонали трапеции, α — угол между диагоналями (можно брать любой угол, т.к. синусы смежных углов равны). Формула применима для любой трапеции. |
*Любая трапеция — это и равнобедренная, и прямоугольная, и тупоугольная, и произвольная 
Площадь круга и кругового сектора.
Площадь многоугольника.
| Формула | Рисунок | Расшифровка формулы |
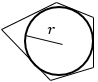 |
р — полупериметр (сумма всех сторон многоугольника, деланная на 2), r — радиус вписанной в этот многоугольник окружности. *Пятиугольник нарисован для примера. Формула работает как для правильного, так и для произвольного многоугольника, главное, чтобы в него можно было вписать окружность. |