Как найти площадь фигуры в другой фигуре

Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Пример:

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см²

Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:

S = a²

Площадь прямоугольника

Пример:

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см²

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м²
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м²

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м²

Ответ: S = 65 м² — площадь огородного участка.

---

Свойство ниже может вам пригодиться при решении задач на площадь.

Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см²

S
_ABC = S_ABCD : 2

S
_ABC = 20 : 2 = 10 см²

S
_ABC =
S
_ACD = 10 см²

---

Ваши комментарии

Оставить комментарий:

---

A combined figure is a geometrical shape that is the combination of many simple geometrical shapes. 

To find the area of combined figures we will follow the steps:

Step I: First we divide the combined figure into its simple geometrical shapes. 

Step II: Then calculate the area of these simple geometrical shapes separately, 

Step III: Finally, to find the required area of the combined figure we need to add or subtract these areas.

Solved Examples on Area of combined figures:

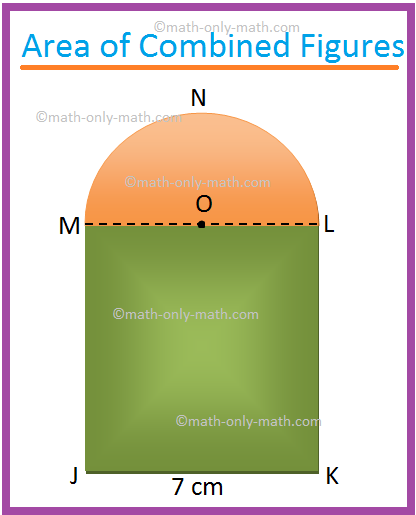
1. Find the area of the shaded region of the adjoining figure. (Use π = (frac{22}{7}))

JKLM is a square of side 7 cm. O is the centre of the
semicircle MNL.

Solution:

Step I: First we divide the combined figure into
its simple geometrical shapes.

The given combined shape is combination of a
square and a semicircle.

Step II: Then calculate the area of
these simple geometrical shapes separately.

Area of the square JKLM = 7² cm²

                                    =
49 cm²

Area of the semicircle LNM = (frac{1}{2}) π ∙ ((frac{7}{2})^{2}) cm² , [Since,
diameter LM = 7 cm]

                                       =
(frac{1}{2})  ∙  (frac{22}{7}) ∙ (frac{49}{4}) cm²

                                       =
(frac{77}{4}) cm²

                                       =
19.25 cm²

Step III: Finally, add these areas up to get
the total area of the combined figure.

Therefore, the required area = 49 cm² + 19.25 cm²

                                          =
68.25 cm².

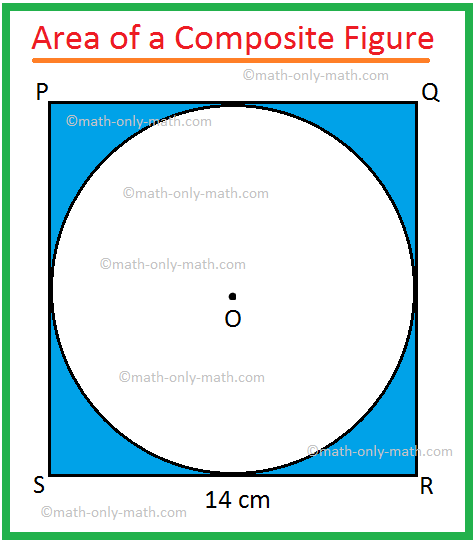
2. In the adjoining figure, PQRS is a square of side 14 cm
and O is the centre of the circle touching all sides of the square. 

Find the area of the shaded region.

Solution:

Step I: First we divide the combined figure into its simple geometrical shapes.

The given combined shape is combination of a square and a circle.

Step II: Then calculate the area of these simple geometrical shapes separately.

Area of the square PQRS = 14² cm²

                                    = 196 cm²

Area of the circle with centre O = π ∙ 7² cm², [Since, diameter SR = 14 cm]

                                             = (frac{22}{7}) ∙ 49 cm²

                                             = 22 × 7 cm²

                                             = 154 cm²

Step III: Finally, to find the required area of the combined figure we need to subtract the area of the circle from the area of the square.

Therefore, the required area = 196 cm² — 154 cm²

                                          = 42 cm²

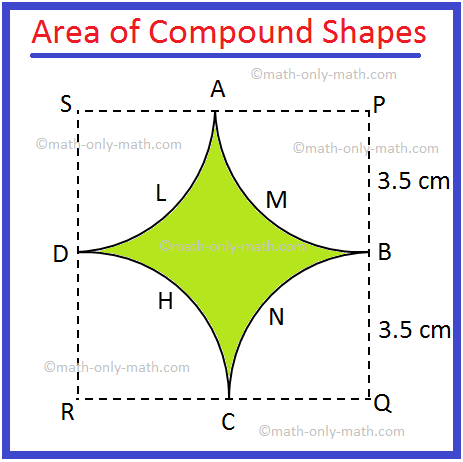
3. In the adjoining figure alongside, there are four equal quadrants of circles each of radius 3.5 cm, their centres being P, Q, R and S. 

Find the area of the shaded region.

Solution:

Step I: First we divide the combined figure into its simple geometrical shapes.

The given combined shape is combination of a square and four quadrants.

Step II:Then calculate the area of these simple geometrical shapes separately.

Area of the square PQRS = 7² cm², [Since, side of the square = 7 cm]

                                                = 49 cm²

Area of the quadrant APB = (frac{1}{4}) π ∙ r² cm²

                                = (frac{1}{4}) ∙ (frac{22}{7})  ∙  ((frac{7}{2})^{2}) cm², [Since, side of the square = 7 cm and radius of the quadrant = (frac{7}{2}) cm]

                                = (frac{77}{8}) cm²

There are four quadrants and they have the same area.

So, total area of the four quadrants = 4 × (frac{77}{8}) cm²

                                                    = (frac{77}{2}) cm²

                                                    = (frac{77}{2}) cm²

Step III: Finally, to find the required area of the combined figure we need to subtract the area of the four quadrants from the area of the square.

Therefore, the required area = 49 cm² — (frac{77}{2}) cm²

                                          = (frac{21}{2}) cm²

                                          = 10.5 cm²

10th Grade Math

From Areas of Combined Figures to HOME PAGE

Расчет площади фигуры является, пожалуй, одной из самых сложных задач теории площадей. В школьной геометрии учат находить области базовых геометрических фигур, таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т. д. Однако часто приходится иметь дело с вычислением площадей более сложных форм. Именно при решении таких задач очень удобно использовать интегральное исчисление.

Пример 1.

Найти площадьфигуры,офаниченной линиями Построить чертеж.

Решение:

Найдем точки пересечения параболы и прямой. Приравняем правые части уравнений, задающих функции, и решим полученное уравнение

Фигура, площадь которой нужно найти, изображена на рисунке. Используя приведенную формулу, получим

Ответ: площадь фигуры равна 13,5 кв. ед.

Вычисление площадей плоских фигур в полярной системе координат

Пусть плоская фигура ограничена линией и лучами

тогда ее площадь можно найти по формуле

Если же фигура ограничена линиями и лучами как на рисунке, то площадь фигуры равна

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Пример 2.

Найти площадь фигуры, ограниченной линией, заданной в полярной системе координат уравнением

Решение:

Ответ: площадь данной фигуры 9,5л кв. ед.

Пример З.

Найти площадь фигуры, ограниченной линиями, заданными в полярной системе координат

Решение:

Фигура, площадь которой требуется найти, показана на рисунке.

Найдем точки пересечения окружности и кардиоиды. Решая совместно данные уравнения, получим точки

По рисунку видно, что фигура симметрична. Вычислим площадь половины фигуры, учитывая, что она в свою очередь разделена на части и (см. рисунок).

Ответ: площадь фигуры

Возможно вам будут полезны данные страницы:

Пример 4.3.

Найти площадь фигуры, ограниченной линиями

Решение:

Из чертежа (см. рис. 7) видно, что искомая площадь криволинейного треугольника равна разности двух площадей: каждая из которых находится по геометрическому смыслу определенного интеграла. Решая систему

получаем, что точка В пересечения прямой и кривой имеет координаты (2;4)

Тогда Окончательно,

Данная задача может быть также решена другим способом. По определению определенного интеграла

Если на то интеграл численно равен площади

криволинейной трапеции, ограниченной кривой и прямыми

Другими словами, в данном случае площадь вычисляется посредством проецирования криволинейной трапеции на ось ординат). Теперь возвращаясь к задаче нашего примера, можем записать:

Если криволинейная трапеция ограничена кривой, заданной в параметрическими уравнениями

прямыми и и отрезком оси то ее площадь вычисляется по формуле где и определяются из равенства

Пример 4.5.

1. Вычислить площадь фигуры, ограниченной линиями: и

Решение:

Решая систему уравнений, находим абсциссы точек пересечения эллипса и параболы Каждое из уравнений разрешаем относительно и учетом симметрии области получаем:

Для вычисления первого интеграла применяем подстановку

Второй интеграл вычисляется непосредственно.

Ответ:

Пример 4.6

Вычислить площадь области, ограниченной эллипсом

Решение:

В силу симметричности эллипса относительно координатных осей вычислим часть области, лежащей в первой четверти, кода и следовательно По формуле а) вычисления площади находим

Пример 4.7

Вычислить площадь области, ограниченной лемнискатой

Решение:

Принимая во внимание симметрию линии относительно полярной оси, получаем:

Пример 4.8

Вычислить площадь фигуры, ограниченной прямыми и кривыми

Решение:

Так как максимум функции достигается в точке и равен а функция на отрезке то

Пример 4.9

Вычислить площадь фигуры, лежащей в первом квадранте, ограниченной линиями и осью

Решение:

Функция

составной график которой ограничивает трапецию сверху, является непрерывной на промежутке

Площадь криволинейной трапеции равна

Пример 5.0

Найти площадь астроиды

Решение:

Запишем уравнение астроиды в параметрическом виде

Здесь удобнее вычислить сначала Отсюда

Вычислить площадь фигуры, ограниченной линиями

Давайте вспомним, как найти площадь прямоугольника. Чтобы найти
площадь прямоугольника, надо длину умножить на ширину.

Вот формула для нахождения площади прямоугольника:

S = a · b

В этой формуле латинской буквой S обозначается площадь, буквами a и b  – стороны прямоугольника.

Выполним задание, в котором надо найти площадь
прямоугольника со сторонами 5 см и 3 см.

Решение. Итак, чтобы найти площадь
прямоугольника, надо его длину умножить на ширину.

Произведение чисел 5 и 3 равно 15. Значит, площадь прямоугольника
равна 15 квадратным сантиметрам. Не забудьте, что площадь измеряется именно в
квадратных единицах. В данной задаче это квадратные сантиметры. Также важно
помнить, что длина и ширина должны быть выражены в одинаковых единицах длины.

3 · 5 =
15 (см²)

Ответ: площадь прямоугольника равна 15 см².

Теперь давайте найдём площадь квадрата со стороной 4 см.

Решение. У этого квадрата каждая
сторона равна 4 см, поэтому умножим 4 на 4 и получится, что площадь квадрата
равна 16 квадратным сантиметрам.

4 · 4 =
16 (см²)

Ответ: площадь квадрата равна 16 см².

Ну а сейчас перейдём к решению задач, в которых нам надо будет
найти площадь сложных фигур.

Найдите площадь фигуры, изображённой на рисунке.

Эта фигура не является ни прямоугольником, ни квадратом. Но мы
можем разделить эту фигуру на два прямоугольника, например, вот таким образом.

 А площади прямоугольников мы легко можем найти с помощью
известной формулы.

Напомним, что противоположные стороны прямоугольника равны.

Итак, стороны первого прямоугольника равны 5 см и 4 см.

5 · 4 =
20 (см²) – площадь первого прямоугольника

Найдём площадь второго прямоугольника.

Ширина этого прямоугольника равна 2 см.

7 – 4 = 3 (см) – длина второго прямоугольника

3 · 2 = 6
(см²) – площадь второго прямоугольника

Мы нашли площади прямоугольников, из которых состоит сложная
фигура. Чтобы найти площадь этой фигуры, надо сложить найденные площади.

20 + 6 = 26
(см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 26 см².

Площадь этой сложной фигуры найти другим способом. Можно разделить
её на два прямоугольника вот таким образом.

Найдём площадь первого прямоугольника.

Одна его сторона равна 4 см.

5 – 2 = 3 (см) – длина стороны первого прямоугольника

4 · 3 =
12 (см²) – площадь первого прямоугольника

Теперь найдём площадь второго прямоугольника.

7 · 2 =
14 (см²) – площадь второго прямоугольника

12 + 14 =
26 (см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 26 см².

Решим следующую задачу.

Найдём площадь ещё одной фигуры, изображённой на рисунке.

Чтобы найти площадь этой фигуры, тоже разделим её на простые
фигуры. Сделаем это вот таким образом.

Получилось 3 прямоугольника.

Найдём площадь первого прямоугольника.

7 · 2 =
14 (см²) – площадь первого прямоугольника

Найдём площадь второго прямоугольника.

7 – 4 = 3 (см) – длина одной стороны второго прямоугольника

8 – 2 – 3 = 3 (см) – длина другой стороны второго прямоугольника

Получается, что это квадрат, так как длина всех его сторон равна 3
см.

3 · 3 = 9
(см²) – площадь квадрата

И найдём площадь последнего прямоугольника.

Его ширина равна 3 см. Длина равна 7 см.

3 · 7 =
21 (см²) – площадь третьего прямоугольника

Таким образом, мы нашли площади всех трёх фигур, на которые
разделили данную сложную фигуру. Площадь этой сложной фигуры найдём как сумму
площадей трёх фигур.

14 + 9 + 21 =
44 (см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 44 см²

Отметим, что площадь этой фигуры можно было бы найти, разделив её
на простые фигуры и вот таким образом:

И решим ещё одну задачу.

Найдите площадь незаштрихованной фигуры.

На рисунке изображён прямоугольник со сторонами 9 см и 5 см.
Внутри этого прямоугольника расположен ещё один прямоугольник со сторонами 5 см
и 3 см. Давайте найдём площадь каждого из них.

9 · 5 =
45 (см²) – площадь большего прямоугольника

5 · 3 =
15 (см²) – площадь меньшего прямоугольника

А как найти площадь незаштрихованной фигуры? Площадь этой фигуры
найдём, если из площади большего прямоугольника вычтем площадь меньшего
прямоугольника.

45 – 15 =
30 (см²) – площадь незаштрихованной фигуры

Ответ: площадь незаштрихованной фигуры равна 30 см².