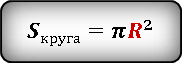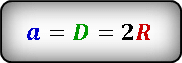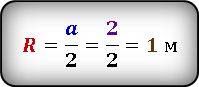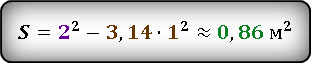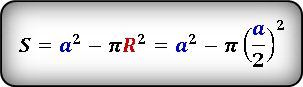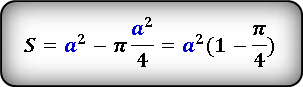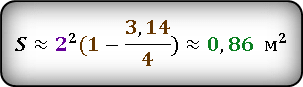Условие задачи:
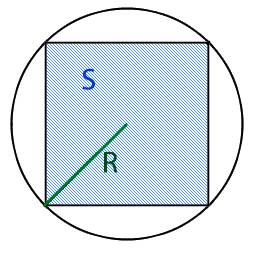
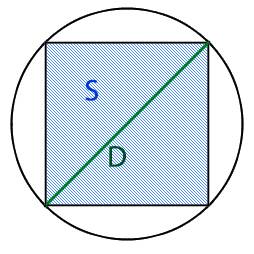
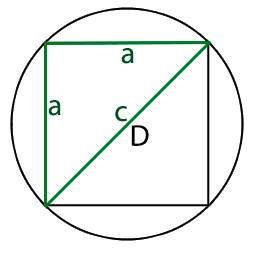
Окружность вписана в квадрат. Найти площадь закрашенной области, если сторона квадрата равна 2 м.
Дано:
Сторона квадрата, a = 2 м
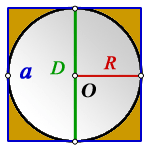
Пояснение к рисунку:
O — центр окружности
R — радиус окружности
D — диаметр окружности
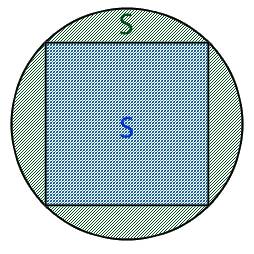
Найти площадь закрашенной области: S
Решение
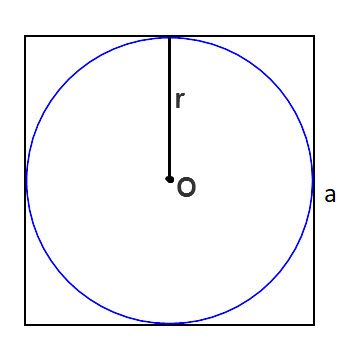
Площадь искомой области можно выразить как разницу между площадью квадрата и площадью круга
Площадь квадрата
Площадь круга
Неизвестен радиус окружности. Из рисунка видно, что сторона квадрата равна диаметру окружности и соответственно удвоенному радиусу
Выразим радиус окружности через сторону квадрата и подставив значение, получим радиус окружности.
Формула площади искомой области на основании выкладок выше, будет выглядеть следующим образом.
Подставив уже известные значения стороны квадрата и радиуса окружности, получаем.
Ответ:
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Если в уже полученное выражение подставить формулу площади круга выраженную через сторону квадрата и преобразовав, получим следующую формулу, в которой площадь закрашенной области, будет сразу выражена через сторону квадрата.
Проверим, подставив наше значение.
Калькулятор для расчета площади закрашенной области
- Подробности
-
Опубликовано: 14 сентября 2017
-
Обновлено: 16 октября 2017
Окружность вписанная в квадрат как найти площадь квадрата
Как определить площадь квадрата
О чем эта статья:
3 класс, 8 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Формула нахождения площади квадрата
Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.
Если известна длина стороны
Умножаем ее на то же число или возводим в квадрат.
S = a × a = a 2 , где S — площадь, a — сторона.
Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.
Если нам дана диагональ
Возводим ее в квадрат и делим на два.
S = d 2 : 2, где d — диагональ.
Если известен радиус вписанной окружности
Умножаем его квадрат на четыре.
S = 4 × r 2 , где r — это радиус вписанной окружности.
Если у нас есть радиус описанной окружности
Возведем его в квадрат и умножим на два.
S = 2 × R 2 , где R — это радиус описанной окружности.
У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь!
Если есть периметр
Мы должны возвести его в квадрат и разделить на 16.
S = Р 2 : 16, где Р — это периметр.
Периметр любого четырехугольника равен сумме длин всех его сторон.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
S квадрата. Решение задач
Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!
Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.
Воспользуемся формулой: S = d 2 : 2.
Подставим в формулу значение диагонали: S = 90 2 : 2 = 4050 мм 2 .
Ответ: 4050 мм 2 .
Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.
Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d
Диаметр окружности равен двум радиусам:
d = 2r
Получается, что сторона равна двум радиусам:
a = 2r
Используем формулу нахождения площади квадрата через сторону:
S = a 2
Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2
Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2
Квадрат вписанный в окружность
Определение
Квадрат, вписанный в окружность — это квадрат, который находится
внутри окружности и соприкасается с ней углами.
На рисунке 1 изображена окружность, описанная около
квадрата и окружность, вписанная в квадрат.
Формулы
Радиус вписанной окружности в квадрат
- Радиус вписанной окружности в квадрат, если известна сторона:
Радиус вписанной окружности в квадрат, если известен периметр:
Радиус вписанной окружности в квадрат, если известна площадь:
Радиус вписанной окружности в квадрат, если известен радиус описанной окружности:
Радиус вписанной окружности в квадрат, если известна диагональ:
Радиус описанной окружности около квадрата
- Радиус описанной окружности около квадрата, если известна сторона:
Радиус описанной окружности около квадрата, если известен периметр:
Радиус описанной окружности около квадрата, если известнаплощадь:
Радиус описанной окружности около квадрата, если известен радиус вписанной окружности:
Радиус описанной окружности около квадрата, если известнадиагональ:
Сторона квадрата
- Сторона квадрата вписанного в окружность, если известнаплощадь:
Сторона квадрата вписанного в окружность, если известнадиагональ:
Сторона квадрата вписанного в окружность, если известен периметр:
Площадь квадрата
- Площадь квадрата вписанного в окружность, если известна сторона:
Площадь квадрата вписанного в окружность, если известен радиус вписанной окружности:
Площадь квадрата вписанного в окружность, если известен радиус описанной окружности:
Площадь квадрата вписанного в окружность, если известен периметр:
Площадь квадрата вписанного в окружность, если известна диагональ:
Периметр квадрата
- Периметр квадрата вписанного в окружность, если известна сторона:
Периметр квадрата вписанного в окружность, если известна площадь:
Периметр квадрата вписанного в окружность, если известенрадиус вписанной окружности:
Периметр квадрата вписанного в окружность, если известен радиус описанной окружности:
Периметр квадрата вписанного в окружность, если известна диагональ:
Диагональ квадрата
- Диагональ квадрата вписанного в окружность, если известна сторона:
Диагональ квадрата вписанного в окружность, если известна площадь:
Диагональ квадрата вписанного в окружность, если известен периметр:
Диагональ квадрата вписанного в окружность, если известен радиус вписанной окружности:
Диагональ квадрата вписанного в окружность, если известен радиус описанной окружности:
Онлайн калькулятор площади вписанного в круг квадрата. Как узнать площадь вписанного в круг квадрата.
Вычислить площадь вписанного квадрата через:
Радиус круга R:
Для того что бы найти площадь вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.
Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:
- либо площадь круга, обозначаемая буквой S,
- либо периметр круга, обозначаемый буквой P,
- либо радиус круга, обозначаемый буквой R,
- либо диаметр круга, обозначаемый буквой D.
Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой
Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга
1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,
мы можем узнать длину сторон квадрата используя теорему Пифагора
после того как мы получили значение длины стороны вписанного квадрата равную a, для получения его площади нам необходимо полученное значение возвести в квадрат.
Квадрат. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):
Можно дать и другие определение квадрата.
Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).
Свойства квадрата
- Длины всех сторон квадрата равны.
- Все углы квадрата прямые.
- Диагонали квадрата равны.
- Диагонали пересекаются под прямым углом.
- Диагонали квадрата являются биссектрисами углов.
- Диагонали квадрата точкой пересечения делятся пополам.
Изложеннные свойства изображены на рисунках ниже:
Диагональ квадрата
Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 . . |
(1) |
Из равенства (1) найдем d:
 . . |
(2) |
Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.
Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:
Ответ:
Окружность, вписанная в квадрат
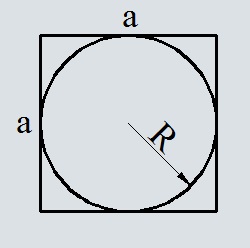
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):
Формула вычисления радиуса вписанной окружности через сторону квадрата
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
 |
(3) |
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
Ответ:
Формула вычисления сторон квадрата через радиус вписанной окружности
Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:
 |
(4) |
Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.
Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:
Ответ:
Окружность, описанная около квадрата
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):
Формула радиуса окружности описанной вокруг квадрата
Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.
Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:
 |
(5) |
Из формулы (5) найдем R:
 |
(6) |
или, умножая числитель и знаменатель на 
 . . |
(7) |
Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.
Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:
Ответ:
Формула стороны квадрата через радиус описанной около квадрата окружности
Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.
Из формулы (1) выразим a через R:
 . . |
(8) |
Пример 5. Радиус описанной вокруг квадрата окружности равен 
Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя 
Ответ:
Периметр квадрата
Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:
 |
(9) |
где 
Пример 6. Сторона квадрата равен 
Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя 
Ответ:
Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.
Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
 |
(10) |
Так как AD и BC перпендикулярны, то
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
 |
(12) |
Эти реугольники также равнобедренные. Тогда
Из (13) следует, что
 |
(14) |
Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
Формулы площади круга вписанного и описанного в треугольник и квадрат.
Площадь круга. Площадь круга вписанного в треугольник и квадрат (описанного около).
Скачайте удобный калькулятор — любые вычисления,
проценты, расчет по формулам, запись и печать результатов
Обозначения:
A, B, C — углы,
a, b, c — стороны,
h — высота,
R — радиус,
S — площадь.
p — полупериметр.
Скачайте удобный калькулятор — любые вычисления,
проценты, расчет по формулам, запись и печать результатов
1. Площадь круга
Где S — площадь круга, R — радиус круга.
2. Площадь круга вписанного в квадрат.
Где a/2 — радиус круга, a — длина стороны квадрата.
3. Площадь круга описанного около квадрата.
Где a — длина стороны квадрата.
В этом случае радиус круга равен 0.5*a*√‾2, используя формулу 1, получаем формулу 3.
4. Площадь круга вписанного в треугольник.
Используя формулу радиуса вписанной окружности
R = (p-a)*tg(A/2)
Где a, A — сторона и противолежащий угол соответственно, p — полупериметр.
Можем записать формулу площади круга вписанного в треугольник:
S = пи * ((p-a)*tg(A/2))²
5. Площадь круга описанного около треугольника.
Используя формулу радиуса описанной окружности
R = a/(2*sin(A))
Где a, A — сторона и противолежащий угол соответственно.
Можем записать формулу площади круга описанного около треугольника:
S = пи * (a/(2*sin(A)))²
6. Формулы полезные в жизни
Часто возникают задачи пересчета объема в площадь или в длину и обратная задача — пересчет площади в объем. Например, доски продаются кубами (кубометрами), а нам требуется рассчитать какую площадь стены можно обшить досками содержащимися в определенном объеме, см. расчет досок, сколько досок в кубе . Или, известны размеры стены, надо рассчитать число кирпичей, см. расчет кирпича.
http://matworld.ru/geometry/kvadrat.php
http://www.clascalc.ru/area-circle.htm
Как найти площадь круга вписанного в квадрат
Вообще мы в прошлый раз определяли площадь круга м², сегодня займёмся площадью круга, который вписан в квадрат! Определим сколько же площадь вписанного круга!
Если мы посмотрим на наш круг вписанный в квадрат, то сразу, наверняка ответили свой вопрос – сколько площадь вписанного круга!?
Если нет, то продолжим…
Формула площади круга вписанного в квадрат
Нам понадобится формула площади круга.
S = πR²
Где S – площадь круга.
π – число Пи (равно 3.14)
R² — квадрат радиуса круга.
Кроме площади круга у нас есть сторона квадрата, которая обозначена буквой «а». И если посмотреть внимательно на нашу картинку. То мы увидим, что сторона квадрата – это диагональ нашего круга, а мы помним, что диагональ в два раза больше радиуса!
В данном случае
R = а/2
И теперь нам нужно данное равенство занести в формулу и мы получим новую формулу- площадь круга вписанного в квадрат…
S = π(а/2)²
Написать что-нибудь…
площадь круга вписанного в квадрат ,
найти площадь круга вписанного в квадрат ,
площадь квадрата вписанного в круг равна ,
площадь квадрата вписанного в круг ,
площадь квадрата вписанного в круг равна ,
формула площади круга вписанного в квадрат ,
Расчёт площади квадрата через площадь окружности, вписанной в этот квадрат
Калькулятор рассчитывает площадь квадрата через площадь окружности вписанной в этот квадрат
Введите площадь окружности Sокр
Формула площади квадрата через площадь окружности вписанной в этот квадрат
Где S — площадь квадрата,
Sокр — площадь окружности
Вывод формулы площади квадрата через площадь окружности вписанной в этот квадрат
Из формулы площади окружности выведем радиус
Сторона квадрата равна двум радиусам
Подставим в формулу площади квадрата
Подставим в формулу выведенный ранее радиус
Похожие калькуляторы
Квадрат — определение и свойства
Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.
Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.
Квадрат относится к правильным многоугольникам. У правильного многоугольника все стороны равны и все углы равны.
Перечислим свойства квадрата:
- Все углы квадрата — прямые, все стороны квадрата — равны.
- Диагонали квадрата равны и пересекаются под прямым углом.
- Диагонали квадрата делятся точкой пересечения пополам.
- Диагонали квадрата являются биссектрисами его углов (делят его углы пополам).
- Диагонали квадрата делят его на 4 равных прямоугольных равнобедренных треугольника:
Периметр квадрата P в 4 раза больше его стороны и равен:
Площадь квадрата равна квадрату его стороны: .
Теорема 1. Диагональ квадрата равна произведению его стороны на , то есть
.
Доказательство:
Рассмотрим квадрат ABCD. Проведем диагональ квадрата AC.
Треугольник АВС – прямоугольный с гипотенузой АС. Запишем для треугольника АВС теорему Пифагора:
что и требовалось доказать.
Теорема 2. Радиус вписанной в квадрат окружности равен половине его стороны:
Доказательство:
Пусть окружность с центром в точке О и радиусом r вписана в квадрат АВСD и касается его сторон в точках
P, M, N, K.
Тогда поскольку AB параллельно CD. Через точку О можно провести только одну прямую, перпендикулярную АВ, поэтому точки Р, О и N лежат на одной прямой. Значит, PN – диаметр окружности. Поскольку АРND – прямоугольник, то PN = AD, то есть
, что и требовалось доказать.
Теорема 3. Радиус описанной около квадрата окружности равен половине его диагонали:
Доказательство:
Диагонали квадрата АС и BD равны, пересекаются в точке О и делятся точкой пересечения пополам. Поэтому OA=OB=OC=OD, т.е. точки A, B, C и D лежат на одной окружности, радиус которой R = d/2 (d=AC=BD). Это и есть описанная около квадрата АВСD окружность.
По теореме
Тогда , что и требовалось доказать.
Заметим, что периметр квадрата тоже можно связать с радиусами вписанной и описанной окружностей:
Четырехугольник является квадратом, если выполняется хотя бы одно из условий:
- Все стороны равны и среди внутренних углов есть прямой угол.
- Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.
Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.
Задача 1. Найдите сторону квадрата, диагональ которого равна .
Решение:
Мы знаем, что . Тогда
.
Ответ: 2.
Задача 2. Найдите площадь квадрата, если его диагональ равна 1.
Первый способ решения:
Зная связь между стороной и диагональю квадрата (теорема 1), выразим сторону квадрата через его диагональ:
Тогда по формуле площади квадрата:
Второй способ решения:
Воспользуемся формулой для площади ромба:
Ответ: 0,5
Задача 3. Найдите радиус окружности, описанной около квадрата со стороной, равной .
Решение:
Радиус описанной окружности равен половине диагонали квадрата, поэтому
Ответ: 2.
Задача 4. Найдите сторону квадрата, описанного около окружности радиуса .
Решение:
Диаметр окружности равен стороне квадрата: .
Ответ: 8.
Задача 5. Радиус вписанной в квадрат окружности равен . Найдите диагональ этого квадрата.
Решение:
Сторона квадрата в два раза больше радиуса вписанной окружности:
Диагональ найдем, зная сторону квадрата:
Ответ: 56.
Задача 6. Радиус вписанной в квадрат окружности равен . Найдите радиус окружности, описанной около этого квадрата.
Решение:
Радиус окружности, вписанной в квадрат, равен половине стороны квадрата, а радиус описанной окружности равен половине диагонали квадрата:
Поэтому
Ответ: 22.
Задача 7. Найдите периметр квадрата, если его площадь равна 9.
Решение:
Найдем сторону квадрата:
Периметр квадрата со стороной 3 равен:
Ответ: 12.
Задача 8. Найдите площадь квадрата, в который вписан круг площадью .
Решение:
Площадь круга откуда радиус круга равен 2.
Сторона квадрата в два раза больше радиуса вписанного круга и равна 4. Площадь квадрата равна 16.
Ответ: 16.
Задача 9. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными .
Решение:
Сторону квадрата найдем как диагональ другого квадрата со стороной 2 клеточки. Поскольку длина одной клеточки равна ., то сторона малого квадрата равна
. А сторона квадрата ABCD равна
Радиус вписанной окружности в два раза меньше стороны квадрата и равен 2.
Ответ: 2.
Задача 10. Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите .
Решение:
Считаем стороны клеток равными единице. Четырехугольник ABCD — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.
Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, AB.
Она равна . Тогда радиус вписанной окружности равен
. В ответ запишем
.
Ответ: 5.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Квадратu0026nbsp;u0026mdash; определение иu0026nbsp;свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023