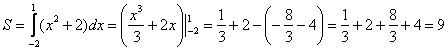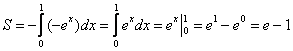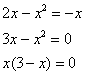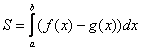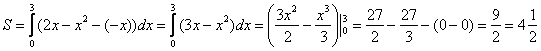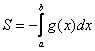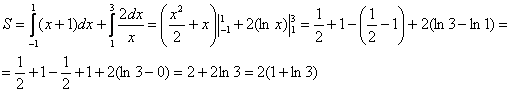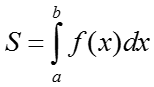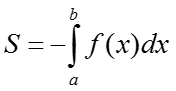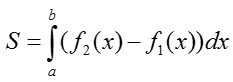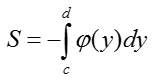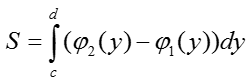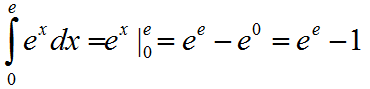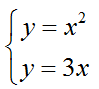Задачка это школьная, но, несмотря на то, почти 100% встретится в вашем курсе высшей математики. Поэтому со всей серьёзностью отнесёмся ко ВСЕМ примерам, и первое, что нужно сделать – это ознакомиться с Приложением Графики функций, чтобы освежить в памяти технику построения элементарных графиков. …Есть? Отлично! Типовая формулировка задания звучит так:
Пример 10
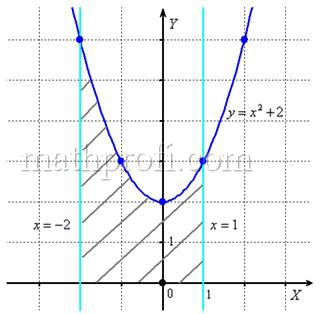
Вычислить площадь фигуры, ограниченной линиями .
И первый важнейший этап решения состоит как раз в построении чертежа. При этом я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций.
В нашей задаче: прямая определяет ось
, прямые
параллельны оси
и парабола
симметрична относительно оси
, для неё находим несколько опорных точек:
Искомую фигуру желательно штриховать:
Второй этап состоит в том, чтобы правильно составить и правильно вычислить определённый интеграл. На отрезке график функции
расположен над осью
, поэтому искомая площадь:
Ответ:
После того, как задание выполнено, полезно взглянуть на чертёж
и прикинуть, реалистичный ли получился ответ.
И мы «на глазок» подсчитываем количество заштрихованных клеточек – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получилось, скажем, 20 квадратных единиц, то, очевидно, где-то допущена ошибка – в построенную фигуру 20 клеток явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.
Пример 11
Вычислить площадь фигуры, ограниченной линиями и осью
Быстренько разминаемся (обязательно!) и рассматриваем «зеркальную» ситуацию – когда криволинейная трапеция расположена под осью :
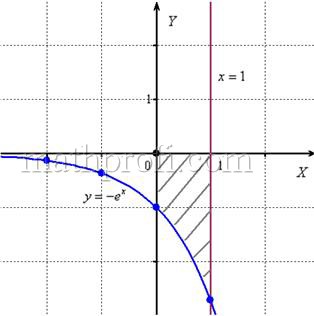
Пример 12
Вычислить площадь фигуры, ограниченной линиями ,
и координатными осями.
Решение: найдём несколько опорных точек для построения экспоненты:
и выполним чертёж, получая фигуру площадью около двух клеток:
Если криволинейная трапеция расположена не выше оси , то её площадь можно найти по формуле:
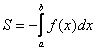
В данном случае:
Ответ: – ну что же, очень и очень похоже на правду.
На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому от простейших школьных задачек мы переходим к более содержательным примерам:
Пример 13
Найти площадь плоской фигуры, ограниченной линиями ,
.
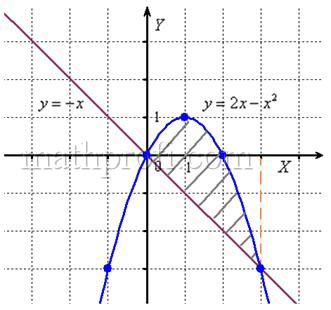
Решение: сначала нужно выполнить чертеж, при этом нас особо интересуют точки пересечения параболы и прямой
, поскольку здесь будут находиться пределы интегрирования. Найти их можно двумя способами. Первый способ – аналитический. Составим и решим уравнение:
таким образом:
Достоинство аналитического способа состоит в его точности, а недостаток – в длительности (и в этом примере нам ещё повезло). Поэтому во многих задачах бывает выгоднее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой».
С прямой всё понятно, а вот для построения параболы удобно найти её вершину, для этого возьмём производную и приравняем её к нулю:
– именно в этой точке и будет находиться вершина. И, в силу симметрии параболы, остальные опорные точки найдём по принципу «влево-вправо»:
Выполним чертеж:
А теперь рабочая формула: если на отрезке некоторая непрерывная функция
больше либо равна непрерывной функции
, то площадь фигуры, ограниченной графиками этих функций и отрезками прямых
, можно найти по формуле:
Здесь уже не надо думать, где расположена фигура – над осью или под осью, а, грубо говоря, важно, какой из двух графиков ВЫШЕ.
В нашем примере очевидно, что на отрезке парабола располагается выше прямой, а поэтому из
нужно вычесть
Завершение решения может выглядеть так:
На отрезке :
, по соответствующей формуле:
Ответ:
Следует отметить, что простые формулы, рассмотренные в начале параграфа – это частные случаи формулы 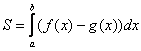
задаётся уравнением
, то одна из функций будет нулевой, и в зависимости от того, выше или ниже лежит криволинейная трапеция, мы получим формулу
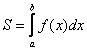
А сейчас пара типовых задач для самостоятельного решения
Пример 14
Найти площадь фигур, ограниченных линиями:
а) ,
.
б) ,
,
Решение с чертежами и краткими комментариями в конце книги
В ходе решения рассматриваемой задачи иногда случается забавный казус. Чертеж выполнен правильно, интеграл решён правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз ошибался ваш покорный слуга. Вот реальный случай из жизни:
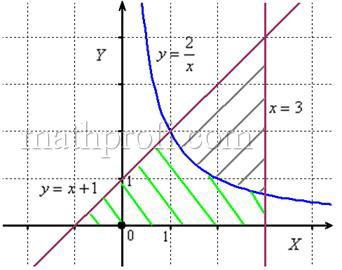
Пример 15
Вычислить площадь фигуры, ограниченной линиями
Решение: выполним бесхитростный чертёж,
хитрость которого состоит в том, что искомая площадь заштрихована зелёным цветом (внимательно смотрИте на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована серым цветом! Особое коварство состоит в том, что прямую можно недочертить до оси
, и тогда мы вовсе не увидим нужную фигуру.
Этот пример ещё и полезен тем, что в нём площадь фигуры считается с помощью двух определённых интегралов. Действительно:
1) на отрезке над осью
расположен график прямой
;
2) на отрезке над осью
расположен график гиперболы
.
Совершенно понятно, что площади можно (и нужно) сложить:
Ответ:
И познавательный пример для самостоятельного решения:
Пример 16
Вычислить площадь фигуры, ограниченной линиями ,
,
и координатными осями.
Итак, систематизируем важные моменты этой задачи:
На первом шаге ВНИМАТЕЛЬНО изучаем условие – КАКИЕ функции нам даны? Ошибки бывают даже здесь, в частности, арккотангенс зачастую принимают за арктангенс. Это, кстати, относится и к другим заданием, где встречается арккотангенс.
Далее следует ПРАВИЛЬНО выполнить чертёж. Сначала лучше построить прямые (если они есть), затем графики других функций (если они есть J). Последние во многих случаях выгоднее строить поточечно – найти несколько опорных точек и аккуратно соединить их линией.
Но здесь могут подстерегать следующие трудности. Во-первых, из чертежа не всегда понятны пределы интегрирования – так бывает, когда они дробные. На mathprofi.ru в соответствующей статье я рассмотрел пример с параболой и прямой
, где из чертежа не понятна одна из точек их пересечения. В таких случаях следует использовать аналитический метод, составляем уравнение:
и находим его корни:
– нижний предел интегрирования,
– верхний предел.
Во-вторых, не всегда понятен «внешний вид» линии, и функция (Пример 16) – яркий тому пример. Я и сам «с ходу» не представляю, как выглядит график этой функции. Здесь можно воспользоваться специализированными программами или онлайн сервисами (а-ля «построить график онлайн»), а в экстремальной ситуации найти побольше опорных точек (штук 10-15), чтобы поточнее провести «неизвестную» кривую.
Ну и, конечно, я призываю вас повышать свои знания и навыки в графиках, в частности, приведу прямую ссылку на особо полезную статью:
http://mathprofi.ru/kak_postroit_grafik_funkcii_s_pomoshyu_preobrazovanii.html
После того, как чертёж построен, анализируем полученную фигуру – ещё раз окидываем взглядом предложенные функции и перепроверяем, ТА ЛИ это фигура. Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части.
Составляем определённый интеграл или несколько интегралов по формуле 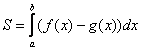
Решаем определённый интеграл (ы). При этом он может оказаться достаточно сложным, и тогда применяем поэтапный алгоритм: 1) находим первообразную и проверяем её дифференцированием, 2) используем формулу Ньютона-Лейбница.
Результат полезно проверить с помощью программного обеспечения / онлайн сервисов или просто «прикинуть» по чертежу по клеточкам. Но и то, и другое не всегда осуществимо, поэтому крайне внимательно относимся к каждому этапу решения!


| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
1. Основная формула для вычисления площади плоских фигур с помощью определенного интеграла
Рассмотрим постановку задачи о площади криволинейной трапеции.
Вычислить площадь криволинейной трапеции, ограниченной линиями (рис. 1).
.
Рис. 1. Площадь криволинейной трапеции
Как мы пытались ее решить:
Первый способ.
Разбили отрезок на
одинаковых отрезков, заменили искомую площадь площадью поступенчастой линии, легко ее сосчитали и получили приближенное решение нашей задачи. Далее устремили
в пределе
и
получили искомую площадь S. Ввели обозначение .
Это определенный интеграл. Вот таким образом мы пытались решить задачу. Мы знаем теперь, как приближенно ее решить, знаем обозначения для точного решения, но точного решения еще не знаем.
Затем мы получили точное решение задачи следующим образом: рис. 2:
Рис. 2. Функция S (x)
Ввели функцию . Каждому
площадь под соответствующей частью кривой
. Так, введенная функция удовлетворяет единственному закону, а именно:
Каждому соответствует единственное значение
.
Мы доказали, что производная этой же функции и доказали, что точная площадь вычисляется следующим образом. Надо найти любую первообразную от функции
и взять приращение этих первообразных. То есть взять первообразную в точке
и отнять первообразную в точке
И в результате мы получили формулу, которой мы будем пользоваться для вычисления площадей.
.
2. Методика нахождения площади на примере
Методику нахождения площади рассмотрим сначала на относительно простом примере.
Пример 1.
Найти площадь фигуры, ограниченной линиями
Решение.
Вот искомая площадь:
Рис. 3. Площадь
Вот формула:
Это общая формула. Конкретно к нашему случаю она применима так:
Пределы интегрирования .
=
.
Вычислили площадь криволинейной фигуры.
Ответ:
В следующей задаче площадь искомой фигуры образовывается с помощью А именно:
3. Пример 2
Найти площадь фигуры, ограниченной линиями
Решение.
Посмотрим, как выглядит фигура (рис. 4).
Рис. 4. Фигура, ограниченная линиями
Формула та же самая:
В нашем случае . Итак, надо найти определенный интеграл
=-(-1)+1=1+1=2.
Искомая площадь найдена, и ответ получен.
Ответ: 2
4. Пример 3
Найти площадь фигуры, ограниченной линиями
Решение.
Рис. 5. Площадь фигуры, ограниченной линиями
Формула для площади та же самая:
В нашем случае .
Ответ:
В следующем примере ищется площадь под параболой.
5. Пример 4
Найти площадь фигуры, ограниченной линиями
Решение.
Схематически изобразим параболу Корни
Рис. 6. Парабола
Применим известную формулу
И применим ее для данной функции и пределов интегрирования
Искомая площадь найдена.
Ответ:
В предыдущих задачах площадь образовывалась с помощью разных кривых, но эта площадь находилась над осью . В следующей задаче наоборот.
6. Пример 5. Случай, если фигура находится под осью
Найти площадь фигуры, ограниченной линиями.
Решение.
Посмотрим, что это за фигура. График в пределах от Π до 2Π расположен под осью Ox (рис. 7).
Рис. 7. График в пределах от Π до 2Π
Ясно, что если возьмем определенный интеграл, то мы получим отрицательное число.
Вычисляем.
1. Сначала вычисляем определенный интеграл от π до 2π от подынтегральной функции
Надо найти первообразную.
По таблице первообразных: .
=-1-1=-2.
2. Для того чтобы найти площадь, надо взять модуль =2.
Ответ: 2.
7. Пример. Общий случай для нахождения площади плоской фигуры, ограниченной двумя кривыми. Выводы
Следующее усложнение – искомая площадь расположена между двумя кривыми.
А именно:
Найти площадь фигуры, ограниченной линиями (рис. 
Рис. 8. Площадь фигуры, ограниченной линиями
Решение.
Итак, площадь образуют 2 кривые, одна из них может находиться под осью .
Каким образом мы будем решать эту задачу?
Во-первых, мы можем сдвинуть фигуру на такое положительное , что площадь находится над осью
. Рис. 9.
Рис. 9. Сдвиг фигуры
Затем мы возьмем соответствующий определенный интеграл и найдем площадь. Искомая площадь равна разности двух площадей.
Площадь под верхней кривой минус площадь под нижней кривой
.
Каждую из площадей мы умеем находить.
Таким образом, в общем виде была поставлена задача, в общем виде получен ответ.
Ответ:
Обсудим и постановку задачи, и полученный важный результат.
Нам надо было найти площадь фигуры, ограниченной линиями
.
Мы использовали известный прием: эту площадь подняли на некоторое , и это
Так вот, эту площадь теперь можно считать без введения
. Правило следующее:
Площадь фигуры, ограниченной прямыми линиями
непрерывных на отрезке
и таких, что для всех
из отрезка
вычисляется по формуле, которую мы вывели:
Рассмотрим первый конкретный пример на нахождение площади между двумя линиями.
8. Пример 6
Найти площадь фигуры, ограниченную линиями
.
Решение. Для начала построим графики этих линий и поймем, где та площадь, которую нам надо искать.
График квадратичной функции – парабола. Корни – 0, 4, ветви вниз. График
– биссектриса первого координатного угла. Вот площадь, которую надо найти:
Рис. 10. Искомая площадь
Но для этого сначала надо найти точки пересечения и решить стандартную задачу.
1. Находим точки пересечения. Для этого решаем систему: .
Отсюда получаем квадратное уравнение относительно :
Мы нашли , то есть, пределы интегрирования. Это первое важное действие.
Теперь стандартное действие:
2. =
=(
)
Искомая площадь равна 4,5
Ответ: 4,5
9. Пример 7. Случай, когда часть площади плоской фигуры лежит под осью
Во втором примере часть площади находится под осью , но на методику это не влияет.
Пример 6.
Итак, требуется найти площадь фигуры, ограниченной линиями
Решение.
Сначала построим графики, посмотрим, какую площадь нам нужно найти. Рис. 11.
Первая функция – парабола, ветви вниз. График второй функции – прямая линия.
Есть две точки пересечения, их придется найти, а именно взять пределы интегрирования, и тогда будем решать задачу по знакомому нам плану.
Рис. 11. Площадь фигуры, ограниченной линиями
Первое действие – найти пределы интегрирования и второе – найти площадь.
Пределы интегрирования найдем из системы.
То есть, пределы интегрирования найдены.
= (
)
Ответ:
Итак, мы показали, каким образом можно вычислять площади плоских фигур с помощью определенного интеграла.
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Ru.scribd.com (Источник).
- Math4you.ru (Источник).
- Dok.opredelim.com (Источник).
Домашнее задание
- Найти площадь фигуры, ограниченной линиями
,
,
,
- Найти площадь фигуры, ограниченной линиями
- Алгебра и начала анализа, Мордкович А.Г.: № 1030, 1033, 1037, 1038.
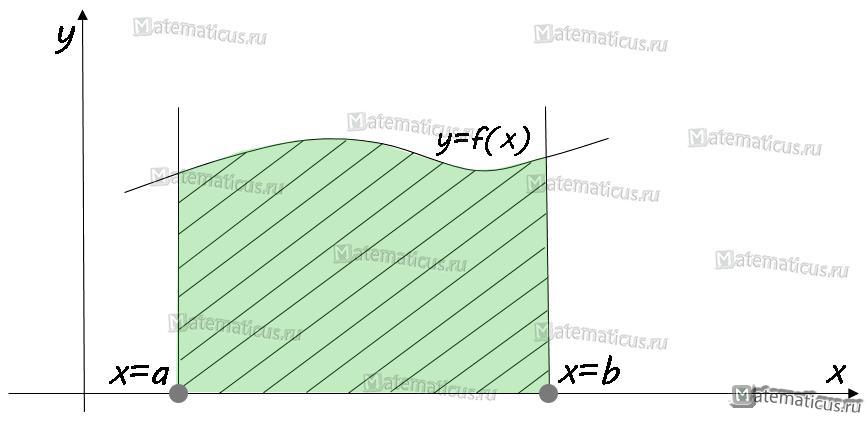
Площадь плоских фигур определяется через определённый интеграл от неотрицательной функции и равна площади криволинейной трапеции. В этом также заключается и геометрический смысл определённого интеграла.
Криволинейной трапецией называется фигура, которая ограничена графиком непрерывной функции f(x)≥0, прямыми x=a, y=b и осью OX.
I. Площадь криволинейной трапеции на оси OX вычисляется по формуле:
II. Если функция f(x)<0, то криволинейная трапеция находится ниже оси OX и тогда её площадь определяется по формуле:
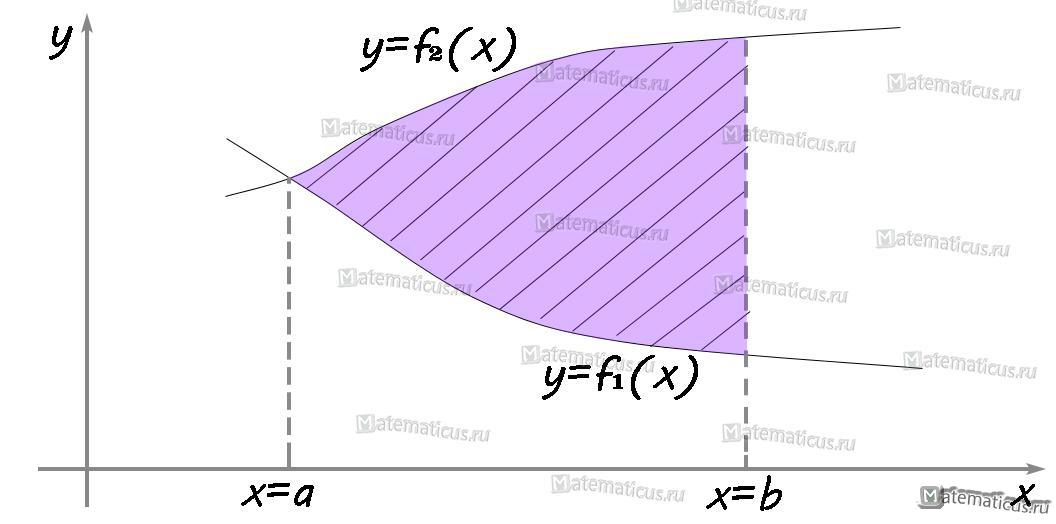
III. Если функция f2(x)≥f1(x), f2(x)-f1(x)≥0 то площадь фигуры находится по формуле:
Читается так: из верхней функции вычитаем нижнюю.
IV. Площадь криволинейной трапеции на оси OY определяется по формуле:
V. Если криволинейная трапеция расположена левее оси OY, то её площадь находится по формуле: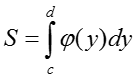
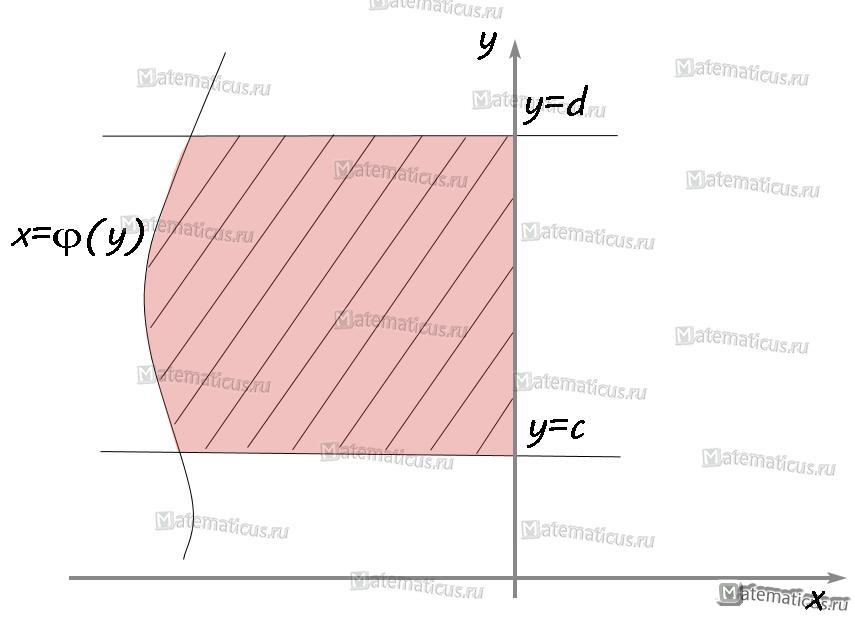
VI. Если функция φ2(x)≥φ1(x), φ2(x)-φ1(x)≥0, то площадь криволинейной трапеции ограниченна графиками x=φ1(x), x=φ2(x) и прямыми y=d, y=c и определяется по формуле:
Если плоская фигура не относится к криволинейной трапеции вышеперечисленных видов, то её разбивают прямыми на криволинейные трапеции, которые параллельны оси OX или OY. Затем используют приведённые формулы выше.
Пример 1
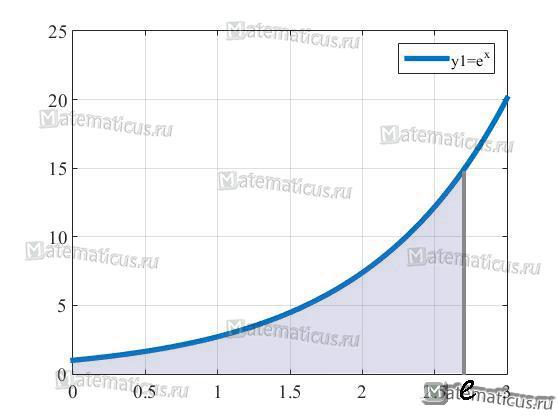
Найти площадь S фигуры, ограниченной функцией f(x)=ex и линиями x=0 и x=e
Решение
Построим график функции f(x)=ex
Пример 2
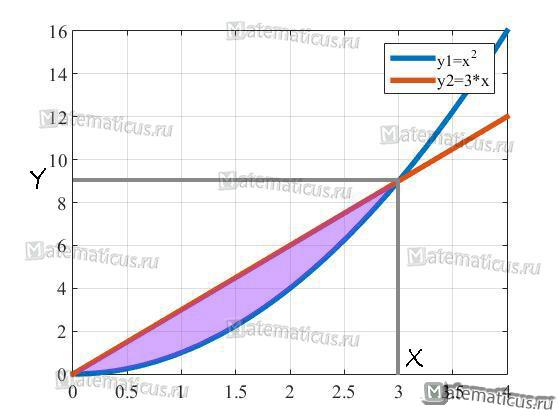
Найти площадь S фигуры, ограниченной линиями y=x2 и y=3x
Решение
Пределами интегрирования являются точки абсциссы пересечения этих функций.
Графически можно представить следующем образом.
Найдем их через решения системы уравнений.
Решая систему находим корни x1=0 и x2=3
$$eqalign{& intlimits_0^3 {3x — {x^2}dx = } cr & = left( {frac{3}{2}{x^2} — frac{1}{3}{x^3}} right)|_0^3 = cr & = frac{{27}}{2} — frac{{27}}{3} = frac{{27}}{6} = 4,5 cr} $$
17318
Вычислить площадь фигуры, ограниченной линиями
Данный калькулятор поможет найти площадь фигуры, ограниченной линиями.
Для того чтобы вычислить площадь фигуры, ограниченной линиями, применяется одно из свойств интеграла. Это свойство аддитивности площадей, интегрируемых на одном и том же отрезке функции.
Аддитивность означает, что площадь замкнутой области, составленных из нескольких фигур, не имеющих общих внутренних точек, равна сумме площадей этих фигур. Интеграл равен площади криволинейной трапеции, ограниченной графиками функций. Вычисление интеграла производится по закону Ньютона-Лейбница, согласно которому результат равен разности первообразной функции от граничных значений интервала.
Калькулятор поможет вычислить площадь фигуры ограниченной линиями онлайн.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Содержание:
- Примеры с решением
Пусть требуется найти площадь фигуры, ограниченной графиками функций 



Каждую площадь можно вычислить как определенный интеграл на заданном промежутке.
Эти суждения можно обобщить следующим образом. 
Так как функции 






По этой ссылке вы найдёте полный курс лекций по высшей математике:
Графики функций не имеют общих точек.
Примеры с решением
Пример 1.
Найдите площадь, ограниченную графиками функций 


Решение:
=
Графики функций пересекаются в двух точках.
Пример 2.
Найдите площадь, ограниченную графиками функций
Решение:
Найдем абсциссы точек пересечения графиков функций.


Полученные значения
Возможно вам будут полезны данные страницы:
Пример 3.
Найдите площадь, заключенную между графиками функций 

Решение:
Найдем абсциссы точек пересечени графиков.
Значит, графики пересекаются в точках с абсциссами 







! Вычислите требуемую площадь при помощи интеграла

Пример 4.
Члены школьного клуба юных конструкторов работают над созданием нового двигателя для автомобиля, который будет меньше засорять окружающую среду. Для нового мотора изменение количества частиц (млрд), загрязняющих атмосферу, в 


a) В какой год они будут выбрасывать в атмосферу одинаковое количество частиц?
b) Какова разница между количеством вредных частиц, выброшенных в атмосферу, за этот период
Решение:
а) при 


Значение 

Пример 5.
Вычислить площадь фигуры, ограниченной параболой 

Решение:
Сначала схематически изобразим эту площадь. Из рисунка видим
что заданные кривые ограничивают две различающиеся плоские фигуры (меньшую и большую). Каждая из этих фигур, в свою очередь, состоит из двух симметричных относительно оси 
Поэтому достаточно вычислить площадь верхней части каждой фигуры и затем умножить ее на два.
Найдем сначала площадь меньшей фигуры. Преобразуем уравнение окружности и определим координаты ее центра и величину радиуса.

Следовательно, центр окружности находится в точке 



уравнений
Найдем уравнение границы 



по этой же причине уравнение нижней части границы 

По формуле (1) находим

но 
— это площадь четверти окружности. Площадь всей окружности равна 

Теперь, чтобы найти площадь большей фигуры, необходимо из площади круга вычесть площадь меньшей фигуры:
Проверим значение первого интеграла







Пример 6.
Вычислить площадь фигуры, ограниченной линиями 
Решение:
Второе уравнение запишем так 









Ветви второй параболы направлены также влево, а ее вершина совпадает с началом координат.
Определим точки пересечения этих кривых из решения системы

Одна точка пересечения 

Изобразим эту фигуру на чертеже. Здесь проще вычислить площадь по формуле (2) т. е.
Лекции:
- Подобие фигур
- Элементарные функции
- Пересекающиеся плоскости
- Как найти производную: примеры решения
- Дифференциальные уравнения примеры решения
- Производная сложной функции
- Многоугольники
- Арифметические операции над пределами
- Метод Гаусса: пример решения
- Производные показательной и логарифмической функций