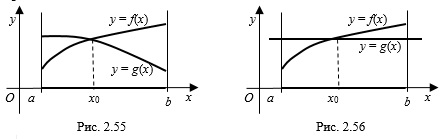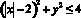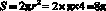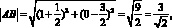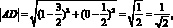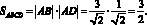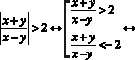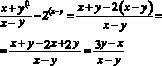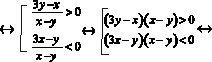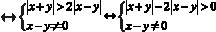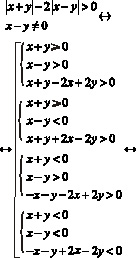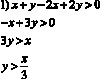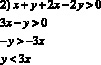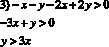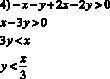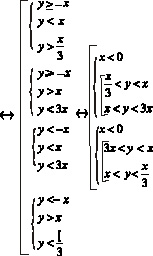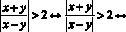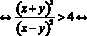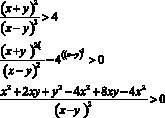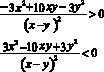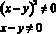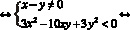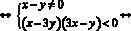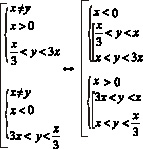Уравнением линии на плоскости называют уравнение с двумя переменными 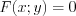



Уравнение окружности
Рассмотрим расположение окружности на координатной плоскости:
1) если уравнение окружности имеет вид 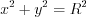


2) если уравнение окружности имеет вид 


Заметим, что неравенству 




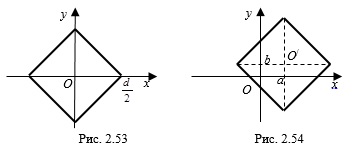
Уравнение квадрата
Рассмотрим расположение квадрата на координатной плоскости:
1) если уравнение квадрата имеет вид 


2) если уравнение квадрата имеет вид 


Пересечение линий на плоскости
Рассмотрим две линии, заданные уравнениями 


Графическое решение уравнений и неравенств
1. Рассмотрим уравнение 



2. Использование монотонности функций при решении уравнений: если функция 





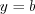
Например, число 

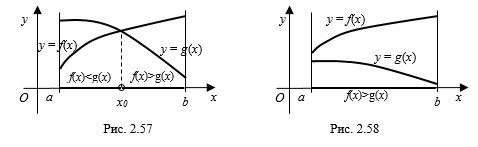
3. Использование монотонности функций при решении неравенств: если функция 
![[a;b] LaTeX formula: [a;b]](https://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png)



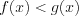

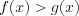
![(x_{0};b] LaTeX formula: (x_{0};b]](https://helpy.quali.me/uploads/formulas/402673c7d0139142c651324cae3880d5bb511595.1.1.png)
Графики функций на заданном отрезке могут и не пересекаться. Например, на рисунке 2.58 неравенство 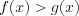
![[a;b] LaTeX formula: [a;b]](https://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png)
Пример 1. Найдите площадь фигуры, ограниченной прямыми 


Решение. Построим на координатной плоскости данные прямые (рис. 2.59).
Прямая 







Из рисунка 2.59 видим, что треугольник 
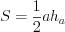

Найдем координаты точек пересечения прямых.
1. Найдем координаты точки 


2. Найдем координаты точки 


3. Найдем координаты точки 


Найдем длину отрезка 









Ответ: 
Пример 2. Найдите площадь фигуры, заданной на координатной плоскости системой неравенств
Решение. Построим гранич-ные прямые, соответствующие неравенствам заданной системы: 





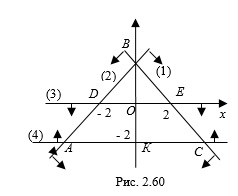
Согласно рисунку 2.60 запишем: 

Найдем координаты точки 





Найдем площадь трапеции: 
Ответ: 
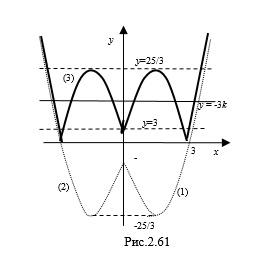
Пример 3. Найдите все целые значений параметра 

Решение. Заменим данное уравнение равносильной системой уравнений 
Построим схематически график функции 


1. Графиком функции 
Согласно формулам 







2. Рассмотрим функцию 




3. Построим график (3) функции 



Рассмотрим линейную функцию 






Ответ: 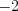
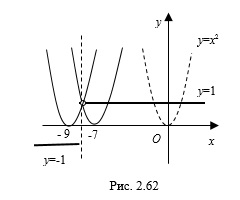
Пример 4. Найдите все значения параметра 

Решение. Решим уравнение графически, заменив его равносильной системой уравнений 
1. Построим схематически график функции 



Рассмотрим два случая:
1) если 


2) если 


2. Построим схематически график функции 

Парабола 














Ответ: 
Построим прямую 


![a=-2sqrt[3]{2} LaTeX formula: a=-2sqrt[3]{2}](https://helpy.quali.me/uploads/formulas/1da946b3ee73655d5d103a1df7688b9505e43c78.1.1.png)
Ответ: ![a=-2sqrt[3]{2} LaTeX formula: a=-2sqrt[3]{2}](https://helpy.quali.me/uploads/formulas/1da946b3ee73655d5d103a1df7688b9505e43c78.1.1.png)
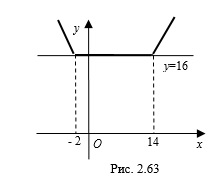
Пример 6. Найдите все значения параметра 
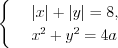
Решение. Имеем уравнение квадрата 

1. Построим квадрат с центром в точке 

Площадь квадрата найдем по формуле 





2. Построим окружность с центром в точке 

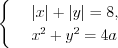






Ответ: 

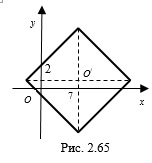
Пример 7. Найдите площадь и периметр фигуры, заданной неравенством 
Решение. Данному неравенству удовлетворяют координаты всех точек плоскости, расположенных внутри квадрата 
Построим квадрат с центром в точке 



С другой стороны площадь квадрата находят по формуле 

Тогда 


Ответ: 

Решая уравнение или систему уравнений графически, точное решение найти бывает достаточно сложно, а то и вовсе не возможно. Поэтому этот метод чаще всего применяют в случае, когда необходимо определить количество корней уравнения или найти их приближенное значение.
Графическое решение систем неравенств
Здесь мы рассмотрим графические решения нескольких систем неравенств. Умение решать такие задачи очень помогает впоследствии, при освоении задач с параметрами.
Задача 1.
Найти площадь фигуры, задаваемой на плоскости множеством решений системы неравенств:
Перепишем иначе:
Рисунок 1
Нас интересует только правая полуплоскость (), область, лежащая выше оси
(
), но ниже прямой
(
) – проведена серым цветом.
Теперь построим графики первых двух функций. Возьмем в решения область ниже зеленой прямой , но выше синей
.
Определим площадь полученной фигуры (залита бежевым) по формуле Пика:
Ответ: 7,5
Задача 2. Найти площадь фигуры, задаваемой на плоскости множеством решений системы неравенств:
Перепишем иначе:
Рисунок 2
Нас интересует только левая полуплоскость (), область, лежащая выше оси
(
), но ниже прямой
(
) – проведена серым цветом.
Теперь построим графики первых двух функций. Возьмем в решения область выше рыжей прямой , но ниже синей
.
Определим площадь данной фигуры путем разбиения ее на простейшие геометрические фигуры: две трапеции. У левой трапеции основания 0,5 и 2, высота 2,5, площадь ее равна
У правой основания 2,5 и 1,5 (она на боку лежит), а высота равна 1. Ее площадь
Общая площадь фигуры равна 5, 125.
Ответ: 5, 125.
Задача 3.
Изобразить на плоскости множество решений системы неравенств. Найти площадь замкнутой части получившейся фигуры:
Вместо исходной системы можем записать совокупность из двух:
и
Первая система имеет решения, но область решений не замкнута.
Рисунок 3
Вторая дает нам искомую замкнутую область:
Рисунок 4
Определим площадь данной фигуры путем разбиения ее на простейшие геометрические фигуры: два треугольника и трапецию. У трапеции основания 1,5 и 2, высота 1, площадь ее равна
У верхнего малого треугольника основание 1, а высота равна 0,5. Его площадь
У правого треугольника основание 1,5, высота – 1, его площадь
Общая площадь фигуры равна 2, 75.
Ответ: 2,75.
Задача 4. Изобразить на плоскости множество решений системы неравенств. При каком значении площадь получившейся фигуры
?
Первое двойное неравенство задает две окружности и область между ними. Две прямые вырезают сектор, показанный на рисунке фиолетовым цветом. Для рисунка был выбран радиус , на самом деле он может быть любым – собственно, его и нужно определить.
Рисунок 5
Так как прямые перпендикулярны (это понятно по их коэффициентам наклона, их произведение – (-1)), то необходимо определить четверть площади кольца.
По условию, эта площадь равна :
Ответ: .
Задача 5.
Изобразить на плоскости множество решений системы неравенств. При каком значении площадь получившейся фигуры
?
Снова имеем окружность, центр ее лежит на прямой , поэтому она вписана в первый координатный угол (квадрант). Причем по условию, нас интересует внешняя часть этой окружности.
Рисунок 6
Из этой внешней части мы возьмем в решения область над осью (
), а по оси
нас интересует полоса от 0 до центра окружности.
Нас интересует маленький, закрашенный зеленым, уголок. Его площадь можно найти как разность площади треугольника и сектора круга. Этот сектор —
часть круга. Поэтому
По условию, эта площадь равна .
Определим :
Ответ: .
- Авторы
- Научный руководитель
- Файлы
- Литература
Дерябина А.А.
1
1 г. Череповец, МБОУ «Женская гуманитарная гимназия», 11 класс
Гущина Г.И. (Череповец, МБОУ «Женская гуманитарная гимназия»)
1. Блох А.Ш., Трухан Т.Л. Неравенства. – Мн. : Народная асвета, 1972.
2. Шахмейстер А.Х. Дробно-рациональные неравенства. – М. : МЦНМО ; СПб. : Петроглиф : Виктория плюс, 2008.
3. Жафяров А.Ж. Математика. ЕГЭ. Решение задач уровня С1. – Новосибирск : Сиб. унив. изд-во, 2010.
4. Иванов М.А. Математика без репетитора. – М. : Вентана-Граф, 2002.
5. Ермолин Е.В., Лукина М.А., Цыпленкова Н.А. Уравнения и неравенства, содержащие модуль.
6. Самарова С.С. Фигуры на координатной плоскости, заданные неравенствами : учебно-методическое пособия для подготовки к ЕГЭ по математике.
7. Конспект урока и подготовка к ЕГЭ [Электронный ресурс]. – Режим доступа: compendium.su.
8. [Электронный ресурс]. – Режим доступа: diffur.kemsu.ru.
9. [Электронный ресурс]. – Режим доступа: ppt4web.ru.
Данная статья является сокращением основной работы. С дополнительными приложениями и фотографиями можно ознакомиться на сайте II Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://www.school-science.ru/2017/7/26525
Цель работы – изучить способы решения неравенств с двумя переменными, содержащих знак модуля.
Поставленная цель обусловила решение ряда задач:
1) изучить теоретический материал о неравенствах и модуле числа, на котором будет основываться исследование;
2) проанализировать практическое применение данного материала посредством решения типовых заданий;
3) рассмотреть различные способы решения неравенств с двумя переменными, содержащих знак модуля;
4) провести анализ сходств и различий данных способов;
5) систематизировать материал и вывести алгоритм решения данных неравенств различными способами;
6) рассмотреть практическое применение данных способов при решении неравенств с двумя переменными, содержащих знак модуля.
Актуальность данной темы обусловлена тем, что задания на неравенства с двумя переменными, содержащими знак модуля, встречаются в заданиях С части ЕГЭ, но не изучаются глубоко в школьном курсе математики (без углубленного изучения).
Объектом исследования являются неравенства с двумя переменными, содержащих знак модуля.
Предметом исследования являются способы решения данных неравенств.
Гипотеза: не все способы решения являются универсальными, поэтому в зависимости от общего вида неравенства и места расположения модуля будем выбирать тот или иной способ решения данных неравенств.
Типовые тестовые задания, содержащие переменную под знаком модуля
Задание № 1. Найти площадь фигуры, заданной неравенством 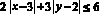
Решение: Множество точек – ромб, полученный из ромба 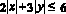
Диагонали ромба: d1 = 6, d2 = 4S = 0,5d1d2 = 0,5 * 4 * 6 = 12.
Ответ: S = 12
Задание № 2. Изобразите на координатной плоскости фигуру, заданную неравенством 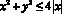
Решение: 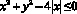
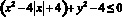
Это два симметричных относительно оси OY круга с центрами в точках (–2;0) и (2;0) и радиусом r =2.
Ответ: 
Задание № 3. Изобразите фигуру, заданную неравенством 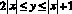
Решение: данная фигура состоит из двух равных треугольников OCB и OAB, вершины которых имеют координаты:
A = (1;2), B = (0;1), C = (–1;2).
Рассмотрим треугольник OAB: основание OB равно 1; высота, опущенная из вершины А к основанию равно 1.
SOAB = 0,5·h·OB = 0,5·1·1 = 0,5 Так как треугольника равные, то S = 2SOAB = 1.
Ответ: S = 1.
Задание № 4. Найдите S фигуры, заданной неравенством 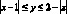
Решение: фигура, заданная неравенством – прямоугольник ABCD с вершинами
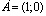
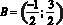
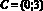
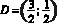
Для нахождения площади необходимы значения сторон AB и AD:
Ответ: S = 1,5.
Задание № 5.
Изобразите фигуру, заданную системой неравенств 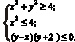
Решение. Первое неравенство системы задает круг с радиусом 2 и центром в начале координат. Второе неравенство задает прямые x = –2 и x = 2, множество точек располагается между этими прямыми. Третьим неравенством задаются прямые y = –2 и y = x, множество точек располагается выше прямой y = –2 и ниже прямой y = x
Фигура является общей частью внутренности прямоугольного треугольника ABC и внешности круга радиусом 2 с центром в начале координат.
Вершины треугольник АBC имеют координаты:
А(–2;–2), В(2;2), С(2;–2)
Найдем площадь прямоугольного треугольника:
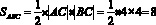
Для того, чтобы вычислить площадь фигуры нужно из площади треугольника ABC вычесть площадь полукруга с радиусом 2:
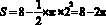
Ответ: 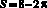
Задание № 6. Найдите площадь фигуры, заданной неравенством 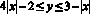
Решение: Фигура состоит их двух равных треугольников OCB и OAB, вершины которых имеют координаты A = (1;2), B = (0;3), C = (–1;2)
Основание треугольника OAB равно 3, а высота, опущенная к основанию из вершины А равна 1.
SOAB = 0,5·h·OB = 0,5·3·1 = 1,5
Треугольники равны, поэтому S = 2SOAB = 3.
Ответ: S = 3.
Задание № 7. Решите систему неравенств:
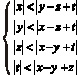
Решение.
Предположим, что данная система неравенств имеет решение x, y, z, t.
Тогда, в частности, 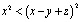
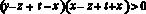
Аналогично получаем:
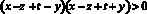
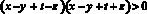
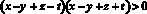
Перемножим все полученные неравенства: с одной стороны, произведение четырех положительных чисел положительно, с другой стороны, это произведение равно:
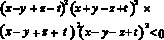
Приходим к противоречию.
Ответ: система не имеет решений.
Задание № 8. Существуют ли действительные числа a, b и с такие, что при всех действительных x и y выполняется неравенство:
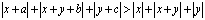
Решение: предположим, такие числа a, b, с существуют. Выберем x > 0 и y > 0 такие, что
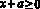
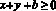
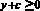
Тогда разность между левой и правой частями равна a + b + с.
Если взять x < 0 и y < 0 такие, что 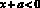
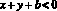
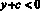
тогда разность будет равна –a – b – с.
Таким образом, с одной стороны a + + b + с > 0, с другой стороны a + b + с < 0, что является противоречием.
Ответ: нет, такие числа не существуют.
Задание № 9. Сколько различных целочисленных решений имеет неравенство 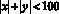
При натуральных n уравнение 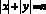
Ответ: 19 801.
Способы решение неравенств с двумя переменными, содержащих знак модуля
Рассмотрим решение неравенств с двумя переменными, содержащие знак модуля, тремя способами:
1. Использование свойств неравенств, путем равносильных преобразований, и правил решения дробных неравенств.
2. Умножение обеих частей неравенства на неотрицательное число и дальнейшее решение полученного неравенства.
3. Возведение обеих частей в квадрат и решение полученного дробно-рационального неравенства.
Для того, чтобы рассмотреть все три способа, берем одно и тоже неравенство:
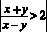
Способ № 1. Использование свойств неравенств, путем равносильных преобразований.
Равносильные переходы при решении неравенств.
Если 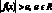
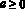
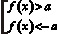
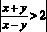
При решении воспользуемся теоремой:
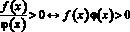
Таким образом данное неравенство равносильно совокупности неравенств:
Перенесем 2 и –2 в левую часть и приведем к общему знаменателю. (1)
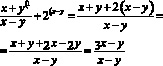
Имеем:
Воспользуемся тем, что
- произведение двух множителей < 0, если каждый множитель > 0 (или каждый < 0);
- произведение двух множителей < 0, если один из множителей < 0, а другой > 0,
и запишем данную совокупность в виде совокупности систем, применив данное чередование к каждому из неравенств. Решим данные совокупности систем неравенств:
Геометрическим решением данного неравенства являются все точки, лежащие в углах АОВ и А1ОВ1, исключая точки, расположенные на лучах ОА, ОD, ОВ и ОА1, ОС, ОВ1.
Способ №1 является наиболее универсальным при решении неравенств. Если неравенство удовлетворяет одному из равносильных переходов, то оно может быть решено данным способом.
Способ № 2. Умножение обеих частей на неотрицательное число
Так как модуль частного равен частному модулей, то:
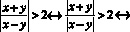
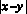
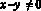
Далее для решения будем использовать метод равносильных преобразований.
Воспользуемся методом одновременного раскрытия модуля и его определением:
Решим данные неравенства:
Геометрическим решением данного неравенства являются все точки, лежащие в углах АОВ и А1ОВ1, исключая точки, расположенные на лучах ОА, ОD, ОВ и ОА1, ОС, ОВ1.
Данный способ наиболее удобен при решении дробно-рациональных неравенств.
Способ №3. Возведение обеих частей в квадрат.
Так как модуль частного равен частному модулей, то:
Так как обе части неравенства – числа неотрицательные, то равносильность не нарушается при возведении в квадрат обеих частей неравенства.
Перенесем 4 в левую сторону и приведем к общему знаменателю.
Таким образом данное неравенство равносильно системе:
Неравенство разложим на множители способом группировки.
Переходим к совокупности систем и решаем с учетом чередования знаков, как при способе равносильных преобразований.
Геометрическим решением данного неравенства являются все точки, лежащие в углах АОВ и А1ОВ1, исключая точки, расположенные на лучах ОА, ОD, ОВ и ОА1, ОС, ОВ1.
Данный способ можно использовать, если обе части неравенства есть числа неотрицательные, а возведение в квадрат не ведет к усложнению решения.
Вывод
Научная новизна исследования:
– рассмотрено три способа решения одного неравенства с двумя переменными, содержащими знак модуля;
– выведен алгоритм для каждого из трех способов решения неравенств;
– даны рекомендации по выбору способа решения;
– представлено приложение с решением неравенств различными способами.
Нужно заметить, что каждый из способов имеет свои преимущества, поэтому для успешного решения данных неравенств необходимо знать все способы. А какой из них наиболее удобный, зависит от вашего решения.
Практическая значимость исследования:
– может быть использовано учителями математики при подготовке к урокам, при изучении тем: «Координаты и графики» и «Решение неравенств», и факультативным занятиям.
– может быть использовано при проведении факультативных занятий и элективных курсов.
– для самостоятельной подготовки учащимися к ЕГЭ и вступительным экзаменам.
Рис. 1. Алгоритм решения неравенств с двумя переменными, содержащих знак модуля
Библиографическая ссылка
Дерябина А.А. НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ, СОДЕРЖАЩИЕ ЗНАК МОДУЛЯ // Международный школьный научный вестник. – 2017. – № 2.
;
URL: https://school-herald.ru/ru/article/view?id=179 (дата обращения: 24.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
СОДЕРЖАНИЕ
1.Введение ……………………………………………………………………3
2.Неравенства с двумя неизвестными………………………………………4-5
3.Системы неравенств………………………………………………………..5-6
4.Применение метода областей при решении
неравенств с двумя неизвестными ……………………………………….6-8
5.Применение метода областей для нахождения площади фигуры,
ограниченной неравенством……………………………………………….9-11
6.Применение метода областей при решении задач с параметром ………12-15
7.Заключение…………………………………………………………………..16
8. Литература …………………………………………………………………..17
Введение
Тема работы посвящена одному из разделов алгебры«Неравенствас двумя неизвестными».
Введение ЕГЭ , и его проведение в течение последних лет, приучила учителей и учеников быть готовыми к любым неожиданностям на экзамене, особенно в части «С». Материал, излагаемый в данной работе, как правило, не встречается в чистом виде в программе школьного курса, но составители текстов ЕГЭ, наверное, подразумевали его изучение на элективных курсах или на дополнительных занятиях
Актуальность темы:
1. Данная тема является дополнением и углублением изученных в курсе алгебры свойств;
2. Приобретение опыта решения задач с использованием метода областей помогает повысить уровень логической культуры;
3. Изучение данной темы помогает более глубоко подготовиться к вступительным экзаменам и ЕГЭ.
Цель работы:
Изучение «метода областей» .
Овладение методами решения задач, связанных с применением «метода областей».
Задачи исследования:
1. Систематизировать теоретически материал по следующим проблемам:
-неравенства с двумя неизвестными;
-системы неравенств с двумя неизвестными.
2. Научиться решать задачи на нахождение:
-множества точек плоскости, координаты, которых удовлетворяют данному неравенству;
-площади фигуры ограниченной неравенством;
-значений параметра.
Неравенства с двумя неизвестными.
Неравенство с двумя неизвестными можно представить так: , где — функция двух переменных х и у. Если мы рассмотрим уравнение , то множество точек , координаты которых удовлетворяют этому уравнению, образует, как правило, некоторую кривую, которая разобьёт плоскость на две или несколько областей. В каждой из этих областей функция сохраняет знак, — остается выбрать те из них, в которых .
Остановимся на самых простейших неравенствах с двумя неизвестными.
1. Рассмотрим, прежде всего, неравенство. Если какой-нибудь из коэффициентов а или отличен от нуля, то уравнение задает прямую, разбивающую плоскость на две полуплоскости. В каждой из них будет сохраняться знак функции . Для определения этого знака достаточно взять любую точку этой полуплоскости и вычислить значение функции в этой точке.
Для того, чтобы убедиться, где находится нужное множество точек, под прямой или над прямой, удобно вычислить значение функции в точке (0,0).
2. Рассмотрим графическое решение ещё одного простого неравенства: .
Ч тобы решить данное неравенство, достаточно рассмотреть функцию , графиком которой является окружность с центром в начале координат и радиусом. Решение неравенств и показано на рисунке.
Заметим, что граница (сама линия, при которой неравенство обращается в уравнение) принадлежит решению лишь в случае, когда неравенство нестрогое. Если неравенство строгое, то граница изображается пунктирной линией, т.е. её точки не входят в область решения неравенства.
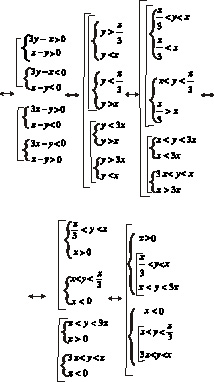
3. На следующих рисунках приведены примеры графического решения наиболее часто встречающихся неравенств с двумя неизвестными.
Системы неравенств.
Решением системы неравенств с двумя переменными называется упорядоченная пара чисел, удовлетворяющая каждому неравенству этой системы.
Для графического изображения решения системы неравенств находят сначала множество Х1точек плоскости, на котором выполняется первое неравенство, потом множество Х2 точек плоскости, где выполняется второе неравенство, и, наконец берут пересечение этих множеств (т.е. их общую часть).
П ример1. Изобразите графически решение системы неравенств .
Р ешение. Неравенство перепишем в виде . Ясно, что оно выполняется на прямой и в точках, лежащих выше этой прямой. Неравенство же выполняется на окружности радиусом 5 с центром в начале координат и внутри неё. Общая часть этих множеств показана на рисунке.
Пример2.. Изобразите графически решение системы неравенств
Решение. Первое неравенство системы перепишем в виде . Ясно, что оно представляет собой внутреннюю область параболы , включая её границу. Второе неравенство системы перепишем в виде . Оно выполняется на параболе и внутри неё. Общая часть этих множеств показана на рисунке.
П ример3. Изобразите графически решение системы неравенств
Решение. Множество решений каждого из неравенств системы есть полуплоскость. Границы первых двух неравенств системы попарно параллельные прямые (их угловые коэффициенты равны), прямые также параллельны. Следовательно, решением данной системы является параллелограмм, изображенный на рисунке.
Применение метода областей
при решении неравенств с двумя неизвестными.
Метод интервалов без существенных изменений переносится с числовой оси на координатную плоскость. При этом роль критических точек на координатной плоскости играют критические линии, а роль промежутков – области. Эти линии делят область определения функции двух переменных на «более мелкие» области, в каждой из которых непрерывная функция сохраняет знак.
Для нахождения этого знака достаточно взять в рассматриваемой области какую-нибудь отдельную «удобную» точку и найти знак функции в выбранной точке, который сохраняется во всей области. При переходе через критические (граничные) линии, знак функции, как правило, не меняется. Случаи, когда знак не меняется, аналогичны случаям критических точек четной кратности.
Схема исследования неравенств с двумя неизвестными методом областей аналогична схеме решения неравенств с одной неизвестной методом интервалов.
Пример4.На координатной плоскости изобразите множество точек , координаты которых удовлетворяют неравенству .
Решение. На координатной плоскости нарисуем линии, определяемые равенствами
, и ,
которые разбивают плоскость на несколько областей. При х = 1, у = 0 левая часть неравенства равна -1. Следовательно, в области, содержащей точку (1; 0), она имеет знак минус, а в остальных областях её знаки чередуются (убедиться в этом дополнительно можно, вычислив знак левой части неравенства в отдельных «удобных» точках каждой области).
О твет: закрашенные области на рисунке.
Пример5.На координатной плоскости изобразите множество точек , координаты которых удовлетворяют неравенству .
Решение. Нарисуем граничные линии
.
Прих = 1, у = 0 левая часть неравенства имеет знак плюс, в соответствии, с чем её знаки распределяются по областям так, как на рисунке.
Ответ: закрашенные области на рисунке.
Пример6.На координатной плоскости изобразите множество точек , координаты которых удовлетворяют неравенству .
Р ешение. ОДЗ: .
В верхней полуплоскости нарисуем линии, определяемые условиями; .
Прих = 0, у = 1 и в соответствующей области дробь имеет знак плюс, который меняется при переходе через граничные линии. Непосредственной проверкой убеждаемся, что при у = 0, неравенство выполняется.
Ответ: закрашенные области на рисунке.
П ример7.На координатной плоскости изобразите множество точек , координаты которых удовлетворяют неравенству
.
Решение. Граничные линии , где — целая часть числа х, и . Затем строим граничные линии и определяем знаки в полученных областях подстановкой отдельных точек.
Ответ: закрашенные области на рисунке.
Пример8.На координатной плоскости изобразите множество точек , координаты которых удовлетворяют неравенству .
Решение. Нарисовав график функции
и отобразив её «верхнюю» часть симметрично относительно оси абсцисс, получим линию, определяемую уравнением . В точке (0; 0) левая часть неравенства имеет знак минус. Следовательно, в области, содержащей точку (0; 0), она имеет знак минус, а в остальных двух областях – знак плюс. Заметим, что в ответ входит луч у = 0, .
Ответ: закрашенные области на рисунке и луч у = 0, .
Пример9.На координатной плоскости изобразите множество точек , координаты которых удовлетворяют неравенству .
Решение. ОДЗ: .
Граничные линии: , и . Строим граничные линии. Они разбивают плоскость на восемь областей, определяя знаки подстановкой в отдельных точках, получаем решение.
Ответ: закрашенные области на рисунке.
Применение метода областей, при решении задач на нахождение площади фигуры ограниченной неравенством.
Вданном разделе представлены задачи, в которых требуется найти площадь фигуры, ограниченной неравенством.
Пример10. Найти площадь фигуры ограниченную неравенством
.
Решение. Поскольку произведение рано нулю лишь в случае, когда хотя бы один из множителей равен нулю, уравнение задаёт линию, распадающуюся на две окружности и . Они делят плоскость на три части. С помощью метода пробных точек устанавливаем, что исходное неравенство выполняется в кольце, ограниченном этими окружностями (на рисунке эта область закрашена).
Найдем площадь полученной фигуры, как разность площадей кругов с радиусами :,.
Ответ. 12 .
Пример11. Найти площадь фигуры ограниченную неравенством .
Р ешение. Начертим оси координат и проведем прямыех = 2 и у = -1. Прямые разбили плоскость на четыре части. Раскрывая последовательно знак модуля в каждой части (против часовой стрелки), получаем: В I части: ;
ВоII части: ;
ВIII части: ;
ВIV части:
Искомая фигура представляет собой внутреннюю область квадрата (на рисунке эта область закрашена). Найдем площадь полученной фигуры, как площадь ромба с равными диагоналями: ,.
Ответ. 2.
П ример12. Найти площадь фигуры ограниченную системой неравенств .
Решение. Первое неравенство содержит внутреннюю часть круга с центром в точке (1; 1) и радиусом 1. Второе неравенство представляет собой внутреннюю часть ромба, центр которого находится в точке (0; 1). Тогда их общее решение находим как пересечение двух областей (на рисунке эта область закрашена). Найдем площадь полученной фигуры, как площадь сектора, а легче как четверть круга: ,так как радиус равен 1.
Ответ..
Пример13. Найти площадь фигуры ограниченную неравенством .
Решение. Преобразуем данное неравенство
.
Первое неравенство системы задает внутреннюю часть круга радиуса 2 с центром в начале координат. Второе неравенство задает множество точек плоскости, для которых и . Объединяя найденные решения, получаем два равных сегмента (на рисунке эта область закрашена).
Площадь, полученной фигуры найдем как удвоенную площадь сегмента. Для этого из площади сектора ОАВ вычтем площадь треугольника ОАВ и удвоим полученный результат.
Треугольник ОВС прямоугольный с катетом ОС = 1 и гипотенузой ОВ = 2, тогда . Катет ВС найдем по теореме Пифагора, .
Площадь сектора найдем по формуле ,.
Найдем площадь треугольника ОАВ:.
Так как у нас два равных сегмента, то площадь искомой фигуры находится по формуле:
О твет: .
Пример14. Найти площадь фигуры ограниченную неравенством .
Решение. Переписав неравенство в виде , и выделив в левой части полный квадрат, получим . Площадь искомой фигуры складывается из площадей четырёх полукругов и одного ромба:
, где R = ,d1 = 4, d2= 8 ,
тогда.
Ответ:.
П ример15. Найдите площадь фигуры ограниченную системой неравенств
.
Решение. Перепишем первое неравенство системы в виде: , выделим в левой части полный квадрат и получим неравенство: . Последнее неравенство определяет на координатной плоскости внутреннюю часть круга с центром в точке (2; 2) и радиусом R = 2.
Второе неравенство системы задает на координатной плоскости верхнюю полуплоскость, ограниченную уравнением . Общее решение системы показано на рисунке штриховкой.
Заметим, что площадь фигуры ограниченную заданной системой неравенств, можно найти как сумму площадей полукруга с радиусом R = 2 и треугольника АВС.
, тогда .
Ответ..
Пример16. Найдите площадь фигуры заданную неравенством .
Р ешение. Построим граничные линии, на которых происходит смена знаков подмодульных выражений: это ось абсцисс, ось ординат и прямая у=х. Эти кривые разбивают плоскость на подобласти их – VI, на каждой из которых строим соответствующие множества точек, удовлетворяющих неравенству . Рассмотрим, учитывая симметричность неравенства три области.
I область: , тогда неравенство принимает вид .
VI область: , тогда неравенство принимает вид .
V область:тогда неравенство принимает вид .
Итак, неравенство , задаёт на координатной плоскости фигуру, показанную на рисунке штриховкой.
Площадь этой фигуры находим как сумму площадей трех квадратов со стороной равной 1.
Ответ. 3.
Применение метода областей для решения заданий с параметром.
Взгляд на параметр как на равноправную переменную находит своё отражение в графических методах. В самом деле, поскольку параметр «равен в правах» с переменной, то ему, естественно, можно «выделить» и свою координатную ось. Таким образом, возникает координатная плоскость (х; а). казалось бы такая незначительная деталь, как отказ от традиционного выбора буквх и у для обозначения осей, определяет один из эффективнейших методов решения задач с параметрами.
Конечно, далеко не все задачи с параметрами можно решить графическим способом. Выделим самые общие признаки, которые помогут узнавать задачи, подходящие под рассматриваемый метод: в задаче фигурирует лишь один параметр а и одна переменная х, они констатируют некоторые аналитические выражения и т.д., графики уравнений строятся в системе координат (х; а) несложно. Сам же процесс решения схематично выглядит так. Вначале строится графический образ, затем, пересекая полученный график прямыми, перпендикулярными параметрической оси, «читаем» нужную информацию.
П ример17. Найти все значения а, при которых система имеет единственное решение.
Решение. Перепишем исходную систему в таком виде: .
Все решения этой системы (пары вида ) образуют область, показанную на рисунке штриховкой.
Требование единственности решения данной системы на графический язык переводится так: горизонтальные прямые должны иметь с полученной областью только одну общую точку. Легко заметить, что лишь прямые и удовлетворяют выдвинутому требованию.
Ответ: или .
Пример18. Найти все значения а, при которых уравнение имеет ровно три корня?
Решение. Исходное уравнение равносильно совокупности , выражая параметр а, получаем: .
График этой совокупности – объединение уголка и параболы. Очевидно, лишь прямая пересекает полученное объединение в трех точках.
Ответ:
Пример19. Сколько решений имеет уравнение в зависимости от значений параметра а?
Р ешение.Данное уравнение решаем аналогично предыдущему. Оно равносильно совокупности следующих двух уравнений:
.
Построим в прямоугольной системе координат графики функций, входящих в совокупность. График этой совокупности – объединение уголка и параболы.
Количество решений данного уравнения при фиксированном значении параметра — это число точек пересечения графика данного уравнения с горизонтальной прямой . По рисунку «считываем» ответ: при ,а= 0 и исходное уравнение имеет два корня, приа = -1 и а = 1 уравнение имеет три корня, при и уравнение имеет четыре корня.
Ответ: если ,а= 0 и , то два корня,
еслиа = -1 и а = 1 , то три корня,
еслии, то четыре корня.
П ример20. Сколько решений имеет уравнение в зависимости от значений параметра а?
Решение. Запишем это уравнение как квадратное относительно а:. Найдем корни и получим следующую совокупность
. Теперь обращение к координатной плоскости (х; а) делает задачу почти тривиальной. Координаты точек пересечения парабол можно найти, решив уравнение . Отсюда . Для записи ответа осталось лишь заметить, что общая точка этих парабол совпадает с вершиной параболы , это точка с координатами . Проводя на рисунке прямые, параллельные оси абсцисс «считываем» ответ.
Ответ. Если , то решений четыре; если , то решений два; если , то решение одно; если , то решений нет.
Пример21. Найти все значения а, при которых любое решение неравенства по модулю не превосходит двух.
Р ешение. Перепишем данное неравенство в таком виде: .
Графики уравнений и разбивают координатную плоскость (х;а) на четыре области. «Методом областей» устанавливаем, что решением исходного неравенства будут заштрихованные на рисунке области. Теперь, если при каком-то фиксированном значении , прямая , в пересечении с полученной областью, дает лишь точки, абсциссы которых удовлетворяют условию , то — одно из искомых значений параметра. Тогда очевидно, что все значения параметраа, из отрезка АВ,удовлетворяют условию задачи, следовательно .
Ответ:
П ример22. Найти все значения параметра а, при каждом из которых множество решений неравенства не содержит ни одного решения неравенства.
Решение. Применим «метод областей» для решения неравенства . Построим граничные линии и , и определим знаки в полученных областях.
Решение неравенства на рисунке показано штриховкой.
В этой же системе координат строим множество точек, определяемых условием(они задают на координатной плоскости «полосу» ) Очевидно искомые значения параметраа те, при которых ни одна из точек указанных областей неравенства не принадлежит «полосе» .
Анализируя полученную картинку, приходим к выводу, что значения параметра, при которых выполняется условие задачи, составляют объединение интервалов .
Ответ: или .
П ример23. Для каких значений параметра а в множестве решений неравенства содержится промежуток ?
Решение. Перепишем данное неравенство в виде:. Запишем совокупность двух систем, равносильную исходному уравнению:
или, откуда или .
Заметим, что в решение первой системы ни при каких значениях параметра а не может входить отрезок , тогда необходимые исследования проведем только для второй системы. Имеем . Обозначим . Тогда второе неравенство системы на координатной плоскости задает множество, показанное на рисунке штриховкой. Теперь, с помощью рисунка, легко установить, что при в полученном множестве содержатся все точки, абсциссы которых пробегают все значения из промежутка . Тогда .
Ответ:.
П ример24. При каких значениях параметра а, уравнение имеет единственное решение?
Решение. Перепишем данное уравнение в виде , заменим его равносильной системой
и построим графический образ в координатной плоскости (х; а). Заметим, что является решением. При исходное уравнение принимает вид , и имеет одно решение . Из рисунка видно, что единственное решение, данное уравнение имеет при значениях параметра . Находим его, выразив хиз второго уравнения системы, т.е. .
Ответ:, при .
Заключение
Основные выводы:
Для успешного освоения предлагаемого материала от учащихся требуется: умение хорошо знать графики элементарных функций, уметь «работать с модулем», решать стандартные уравнения и неравенства, а так же иметь навыки вычисления выражений при конкретных значениях переменной.
Значимость данной работы:
При решении задач мы пришли к выводу, что:
метод областей, есть не что иное, как перенос метода интервалов с прямой на плоскость, он позволяет увидеть красоту математических выкладок и эстетику графического подхода к решению неравенств с двумя переменными;
наша работа может быть использована для проведения практических занятий на элективных курсах с учащимися выпускных классов и при подготовке к Единому Государственному экзамену.
Список литературы.
Севрюков П.Ф. «Тригонометрические, показательные и логарифмические уравнения и неравенства: учебное пособие Изд. 2 доп. М. : Илекса;Народное образование; Ставрополь: Сервисшкола, 2010. – (Серия «Изучение сложных тем школьного курса математики»)»
Математика. Подготовка к ЕГЭ-2011: учебно – методическое пособие / Под редакцией Ф.Ф.Лысенко, С.Ю.Кулабухова. – Ростов – на -Дону: Легион- М,2010.
Математика. Всё для ЕГЭ 2011. Часть 1: учебно-методическое пособие / Под ред. Д.А.Мальцева. – Ростов н/Д:Издатель Мальцев Д.А.; М.:НИИ школьных технологий, 2010.
П.И. Горнштейн, В. Б. Полонский, М.С. Якир. Задачи с параметрами. – М.: Илекса, Харьков: Гимназия, 2003.
Замечательные неравенства: способы получения и примеры применения. 10-11 кл.: учебное пособие / С.А.Гомонов. – 2-е изд., стереотип. –М.: Дрофа, 2006.(Элективные курсы).
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/143881-metod-oblastej