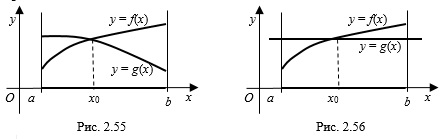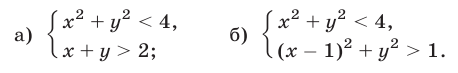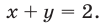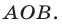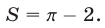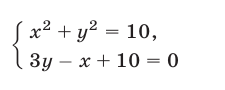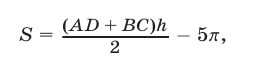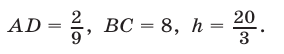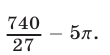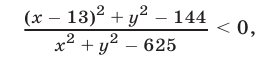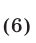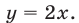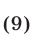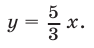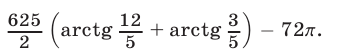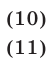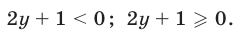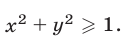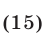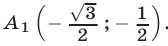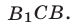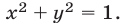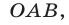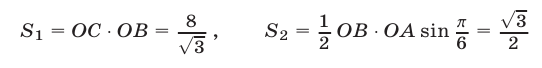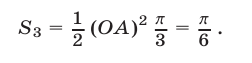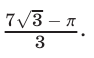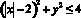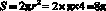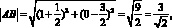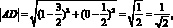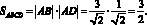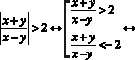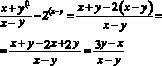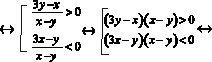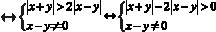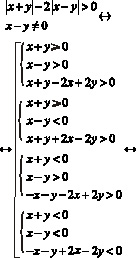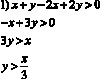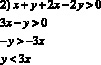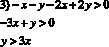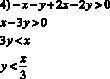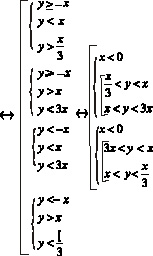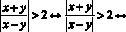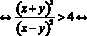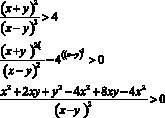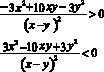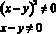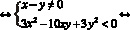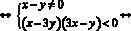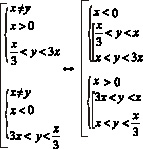Графическое решение систем неравенств
Здесь мы рассмотрим графические решения нескольких систем неравенств. Умение решать такие задачи очень помогает впоследствии, при освоении задач с параметрами.
Задача 1.
Найти площадь фигуры, задаваемой на плоскости множеством решений системы неравенств:
Перепишем иначе:
Рисунок 1
Нас интересует только правая полуплоскость (), область, лежащая выше оси
(
), но ниже прямой
(
) – проведена серым цветом.
Теперь построим графики первых двух функций. Возьмем в решения область ниже зеленой прямой , но выше синей
.
Определим площадь полученной фигуры (залита бежевым) по формуле Пика:
Ответ: 7,5
Задача 2. Найти площадь фигуры, задаваемой на плоскости множеством решений системы неравенств:
Перепишем иначе:
Рисунок 2
Нас интересует только левая полуплоскость (), область, лежащая выше оси
(
), но ниже прямой
(
) – проведена серым цветом.
Теперь построим графики первых двух функций. Возьмем в решения область выше рыжей прямой , но ниже синей
.
Определим площадь данной фигуры путем разбиения ее на простейшие геометрические фигуры: две трапеции. У левой трапеции основания 0,5 и 2, высота 2,5, площадь ее равна
У правой основания 2,5 и 1,5 (она на боку лежит), а высота равна 1. Ее площадь
Общая площадь фигуры равна 5, 125.
Ответ: 5, 125.
Задача 3.
Изобразить на плоскости множество решений системы неравенств. Найти площадь замкнутой части получившейся фигуры:
Вместо исходной системы можем записать совокупность из двух:
и
Первая система имеет решения, но область решений не замкнута.
Рисунок 3
Вторая дает нам искомую замкнутую область:
Рисунок 4
Определим площадь данной фигуры путем разбиения ее на простейшие геометрические фигуры: два треугольника и трапецию. У трапеции основания 1,5 и 2, высота 1, площадь ее равна
У верхнего малого треугольника основание 1, а высота равна 0,5. Его площадь
У правого треугольника основание 1,5, высота – 1, его площадь
Общая площадь фигуры равна 2, 75.
Ответ: 2,75.
Задача 4. Изобразить на плоскости множество решений системы неравенств. При каком значении площадь получившейся фигуры
?
Первое двойное неравенство задает две окружности и область между ними. Две прямые вырезают сектор, показанный на рисунке фиолетовым цветом. Для рисунка был выбран радиус , на самом деле он может быть любым – собственно, его и нужно определить.
Рисунок 5
Так как прямые перпендикулярны (это понятно по их коэффициентам наклона, их произведение – (-1)), то необходимо определить четверть площади кольца.
По условию, эта площадь равна :
Ответ: .
Задача 5.
Изобразить на плоскости множество решений системы неравенств. При каком значении площадь получившейся фигуры
?
Снова имеем окружность, центр ее лежит на прямой , поэтому она вписана в первый координатный угол (квадрант). Причем по условию, нас интересует внешняя часть этой окружности.
Рисунок 6
Из этой внешней части мы возьмем в решения область над осью (
), а по оси
нас интересует полоса от 0 до центра окружности.
Нас интересует маленький, закрашенный зеленым, уголок. Его площадь можно найти как разность площади треугольника и сектора круга. Этот сектор —
часть круга. Поэтому
По условию, эта площадь равна .
Определим :
Ответ: .
Уравнением линии на плоскости называют уравнение с двумя переменными 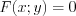



Уравнение окружности
Рассмотрим расположение окружности на координатной плоскости:
1) если уравнение окружности имеет вид 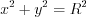


2) если уравнение окружности имеет вид 


Заметим, что неравенству 




Уравнение квадрата
Рассмотрим расположение квадрата на координатной плоскости:
1) если уравнение квадрата имеет вид 


2) если уравнение квадрата имеет вид 


Пересечение линий на плоскости
Рассмотрим две линии, заданные уравнениями 


Графическое решение уравнений и неравенств
1. Рассмотрим уравнение 



2. Использование монотонности функций при решении уравнений: если функция 





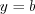
Например, число 

3. Использование монотонности функций при решении неравенств: если функция 
![[a;b] LaTeX formula: [a;b]](https://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png)



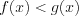

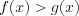
![(x_{0};b] LaTeX formula: (x_{0};b]](https://helpy.quali.me/uploads/formulas/402673c7d0139142c651324cae3880d5bb511595.1.1.png)
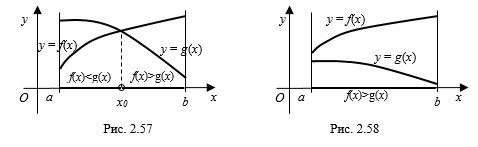
Графики функций на заданном отрезке могут и не пересекаться. Например, на рисунке 2.58 неравенство 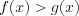
![[a;b] LaTeX formula: [a;b]](https://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png)
Пример 1. Найдите площадь фигуры, ограниченной прямыми 


Решение. Построим на координатной плоскости данные прямые (рис. 2.59).
Прямая 







Из рисунка 2.59 видим, что треугольник 
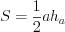

Найдем координаты точек пересечения прямых.
1. Найдем координаты точки 


2. Найдем координаты точки 


3. Найдем координаты точки 


Найдем длину отрезка 









Ответ: 
Пример 2. Найдите площадь фигуры, заданной на координатной плоскости системой неравенств
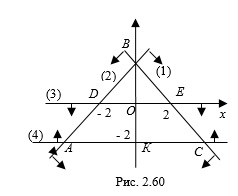
Решение. Построим гранич-ные прямые, соответствующие неравенствам заданной системы: 





Согласно рисунку 2.60 запишем: 

Найдем координаты точки 





Найдем площадь трапеции: 
Ответ: 
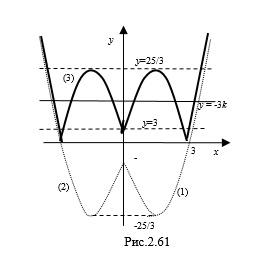
Пример 3. Найдите все целые значений параметра 

Решение. Заменим данное уравнение равносильной системой уравнений 
Построим схематически график функции 


1. Графиком функции 
Согласно формулам 







2. Рассмотрим функцию 




3. Построим график (3) функции 



Рассмотрим линейную функцию 






Ответ: 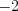
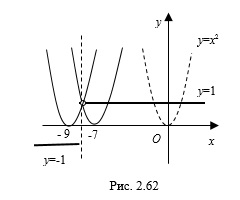
Пример 4. Найдите все значения параметра 

Решение. Решим уравнение графически, заменив его равносильной системой уравнений 
1. Построим схематически график функции 



Рассмотрим два случая:
1) если 


2) если 


2. Построим схематически график функции 

Парабола 














Ответ: 
Построим прямую 


![a=-2sqrt[3]{2} LaTeX formula: a=-2sqrt[3]{2}](https://helpy.quali.me/uploads/formulas/1da946b3ee73655d5d103a1df7688b9505e43c78.1.1.png)
Ответ: ![a=-2sqrt[3]{2} LaTeX formula: a=-2sqrt[3]{2}](https://helpy.quali.me/uploads/formulas/1da946b3ee73655d5d103a1df7688b9505e43c78.1.1.png)
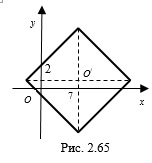
Пример 6. Найдите все значения параметра 
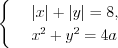
Решение. Имеем уравнение квадрата 

1. Построим квадрат с центром в точке 

Площадь квадрата найдем по формуле 





2. Построим окружность с центром в точке 

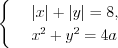






Ответ: 

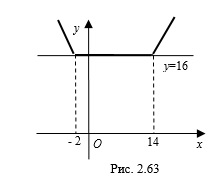
Пример 7. Найдите площадь и периметр фигуры, заданной неравенством 
Решение. Данному неравенству удовлетворяют координаты всех точек плоскости, расположенных внутри квадрата 
Построим квадрат с центром в точке 



С другой стороны площадь квадрата находят по формуле 

Тогда 


Ответ: 

Решая уравнение или систему уравнений графически, точное решение найти бывает достаточно сложно, а то и вовсе не возможно. Поэтому этот метод чаще всего применяют в случае, когда необходимо определить количество корней уравнения или найти их приближенное значение.
Примеры с решениями
Пример №323.
Изобразить на координатной плоскости 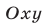
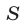
Решение:
а) Неравенство 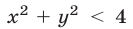
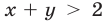
Эта прямая пересекает окружность в точках 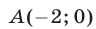
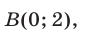
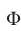
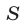
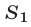
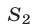
Так как 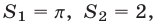
б) Фигура 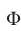
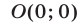
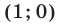
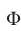
Пример №324.
Найти площадь фигуры 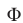
Решение:
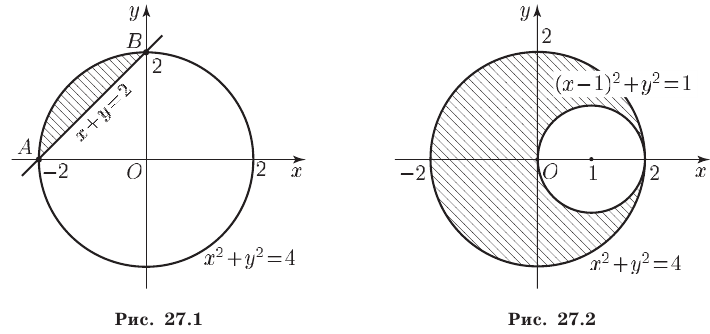
Неравенство (1) определяет множество точек, лежащих вне и на границе круга с центром в точке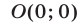
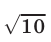
Решив неравенство (2), получим 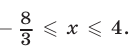

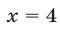
Наконец, неравенству (3) удовлетворяют точки множества 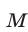
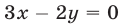
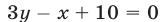
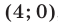
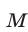
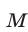
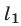
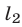
Прямая 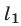
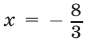
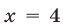
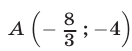
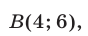
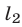
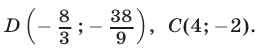
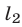
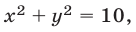
имеет единственное решение 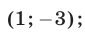
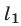
Итак, фигура 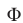
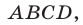
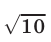
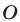
где
Ответ.
Пример №325.
На координатной плоскости рассматривается фигура 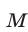
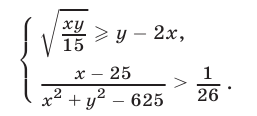
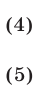
Изобразить фигуру 
Решение:
Неравенство (5), равносильное неравенству
является верным в тех и только в тех точках плоскости 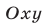
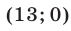
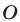
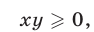
т. е. для точек I и III квадрантов. Считая условие (6) выполненным, рассмотрим два возможных случая:
1) Если
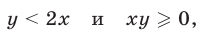
то неравенство (4) является верным. Система неравенств (7) задает множество точек I и III квадрантов, лежащих ниже прямой
2) Если
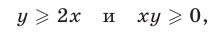
то неравенство (4) равносильно каждому из неравенств
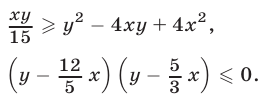
Условиями (8), (9) определяется множество тех точек I квадранта, которые заключены между прямыми 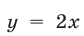
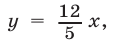
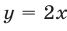
Заметим, что прямая 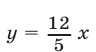
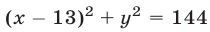
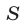
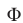
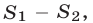
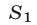
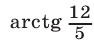
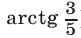
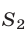
Ответ.
Пример №326.
Найти площадь фигуры 
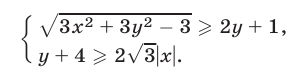
Решение:
Область определения неравенства (10), а значит, и системы (10), (11) задается условием 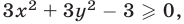
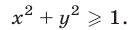
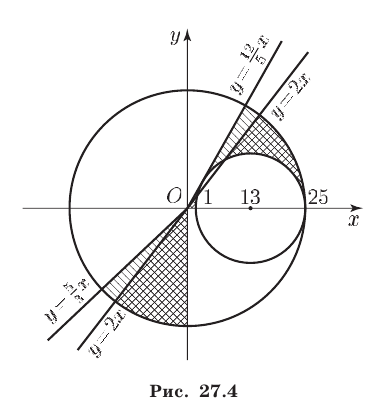
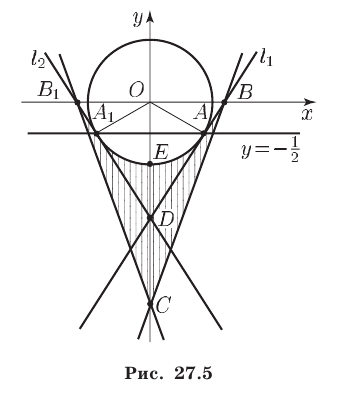
Неравенство (12) определяет область, внешнюю по отношению к кругу с центром в начале координат и радиусом 1 (включая границу круга, рис. 27.5).
Возможны два случая:
1) Если 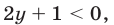
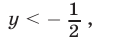
то неравенство (10) является верным на множестве
2) Если 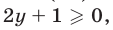
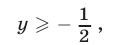
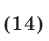
то неравенство (10) равносильно каждому из неравенств
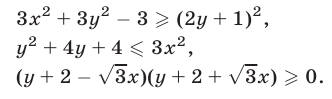
Прямые 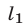
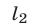
проходят через точку 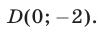
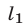
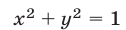
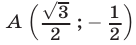
имеет единственное решение 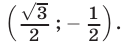
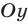
В точке 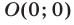
Рассмотрим неравенство (11). Уравнение
задает два луча, выходящие из точки 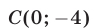
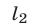
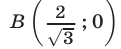
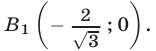
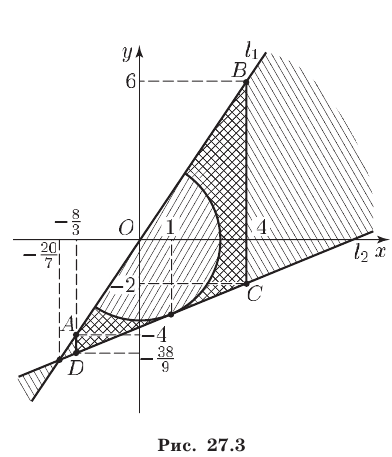
Итак, множеством точек, удовлетворяющих системе неравенств (10), (11) является фигура 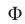
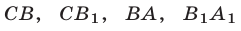
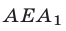
Площадь фигуры 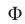
где 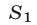
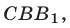
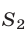
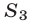
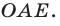
(так как 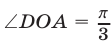
Ответ.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Решение задач по математике
Возможно вам будут полезны эти страницы:
- Авторы
- Научный руководитель
- Файлы
- Литература
Дерябина А.А.
1
1 г. Череповец, МБОУ «Женская гуманитарная гимназия», 11 класс
Гущина Г.И. (Череповец, МБОУ «Женская гуманитарная гимназия»)
1. Блох А.Ш., Трухан Т.Л. Неравенства. – Мн. : Народная асвета, 1972.
2. Шахмейстер А.Х. Дробно-рациональные неравенства. – М. : МЦНМО ; СПб. : Петроглиф : Виктория плюс, 2008.
3. Жафяров А.Ж. Математика. ЕГЭ. Решение задач уровня С1. – Новосибирск : Сиб. унив. изд-во, 2010.
4. Иванов М.А. Математика без репетитора. – М. : Вентана-Граф, 2002.
5. Ермолин Е.В., Лукина М.А., Цыпленкова Н.А. Уравнения и неравенства, содержащие модуль.
6. Самарова С.С. Фигуры на координатной плоскости, заданные неравенствами : учебно-методическое пособия для подготовки к ЕГЭ по математике.
7. Конспект урока и подготовка к ЕГЭ [Электронный ресурс]. – Режим доступа: compendium.su.
8. [Электронный ресурс]. – Режим доступа: diffur.kemsu.ru.
9. [Электронный ресурс]. – Режим доступа: ppt4web.ru.
Данная статья является сокращением основной работы. С дополнительными приложениями и фотографиями можно ознакомиться на сайте II Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://www.school-science.ru/2017/7/26525
Цель работы – изучить способы решения неравенств с двумя переменными, содержащих знак модуля.
Поставленная цель обусловила решение ряда задач:
1) изучить теоретический материал о неравенствах и модуле числа, на котором будет основываться исследование;
2) проанализировать практическое применение данного материала посредством решения типовых заданий;
3) рассмотреть различные способы решения неравенств с двумя переменными, содержащих знак модуля;
4) провести анализ сходств и различий данных способов;
5) систематизировать материал и вывести алгоритм решения данных неравенств различными способами;
6) рассмотреть практическое применение данных способов при решении неравенств с двумя переменными, содержащих знак модуля.
Актуальность данной темы обусловлена тем, что задания на неравенства с двумя переменными, содержащими знак модуля, встречаются в заданиях С части ЕГЭ, но не изучаются глубоко в школьном курсе математики (без углубленного изучения).
Объектом исследования являются неравенства с двумя переменными, содержащих знак модуля.
Предметом исследования являются способы решения данных неравенств.
Гипотеза: не все способы решения являются универсальными, поэтому в зависимости от общего вида неравенства и места расположения модуля будем выбирать тот или иной способ решения данных неравенств.
Типовые тестовые задания, содержащие переменную под знаком модуля
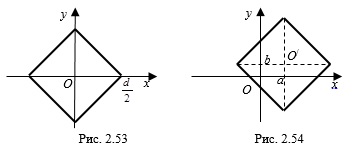
Задание № 1. Найти площадь фигуры, заданной неравенством 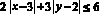
Решение: Множество точек – ромб, полученный из ромба 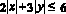
Диагонали ромба: d1 = 6, d2 = 4S = 0,5d1d2 = 0,5 * 4 * 6 = 12.
Ответ: S = 12
Задание № 2. Изобразите на координатной плоскости фигуру, заданную неравенством 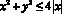
Решение: 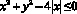
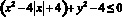
Это два симметричных относительно оси OY круга с центрами в точках (–2;0) и (2;0) и радиусом r =2.
Ответ: 
Задание № 3. Изобразите фигуру, заданную неравенством 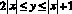
Решение: данная фигура состоит из двух равных треугольников OCB и OAB, вершины которых имеют координаты:
A = (1;2), B = (0;1), C = (–1;2).
Рассмотрим треугольник OAB: основание OB равно 1; высота, опущенная из вершины А к основанию равно 1.
SOAB = 0,5·h·OB = 0,5·1·1 = 0,5 Так как треугольника равные, то S = 2SOAB = 1.
Ответ: S = 1.
Задание № 4. Найдите S фигуры, заданной неравенством 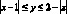
Решение: фигура, заданная неравенством – прямоугольник ABCD с вершинами
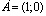
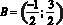
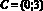
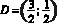
Для нахождения площади необходимы значения сторон AB и AD:
Ответ: S = 1,5.
Задание № 5.
Изобразите фигуру, заданную системой неравенств 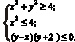
Решение. Первое неравенство системы задает круг с радиусом 2 и центром в начале координат. Второе неравенство задает прямые x = –2 и x = 2, множество точек располагается между этими прямыми. Третьим неравенством задаются прямые y = –2 и y = x, множество точек располагается выше прямой y = –2 и ниже прямой y = x
Фигура является общей частью внутренности прямоугольного треугольника ABC и внешности круга радиусом 2 с центром в начале координат.
Вершины треугольник АBC имеют координаты:
А(–2;–2), В(2;2), С(2;–2)
Найдем площадь прямоугольного треугольника:
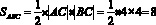
Для того, чтобы вычислить площадь фигуры нужно из площади треугольника ABC вычесть площадь полукруга с радиусом 2:
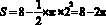
Ответ: 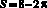
Задание № 6. Найдите площадь фигуры, заданной неравенством 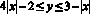
Решение: Фигура состоит их двух равных треугольников OCB и OAB, вершины которых имеют координаты A = (1;2), B = (0;3), C = (–1;2)
Основание треугольника OAB равно 3, а высота, опущенная к основанию из вершины А равна 1.
SOAB = 0,5·h·OB = 0,5·3·1 = 1,5
Треугольники равны, поэтому S = 2SOAB = 3.
Ответ: S = 3.
Задание № 7. Решите систему неравенств:
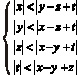
Решение.
Предположим, что данная система неравенств имеет решение x, y, z, t.
Тогда, в частности, 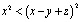
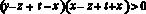
Аналогично получаем:
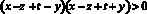
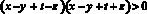
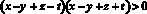
Перемножим все полученные неравенства: с одной стороны, произведение четырех положительных чисел положительно, с другой стороны, это произведение равно:
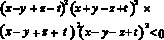
Приходим к противоречию.
Ответ: система не имеет решений.
Задание № 8. Существуют ли действительные числа a, b и с такие, что при всех действительных x и y выполняется неравенство:
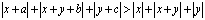
Решение: предположим, такие числа a, b, с существуют. Выберем x > 0 и y > 0 такие, что
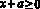
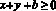
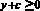
Тогда разность между левой и правой частями равна a + b + с.
Если взять x < 0 и y < 0 такие, что 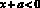
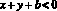
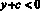
тогда разность будет равна –a – b – с.
Таким образом, с одной стороны a + + b + с > 0, с другой стороны a + b + с < 0, что является противоречием.
Ответ: нет, такие числа не существуют.
Задание № 9. Сколько различных целочисленных решений имеет неравенство 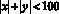
При натуральных n уравнение 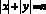
Ответ: 19 801.
Способы решение неравенств с двумя переменными, содержащих знак модуля
Рассмотрим решение неравенств с двумя переменными, содержащие знак модуля, тремя способами:
1. Использование свойств неравенств, путем равносильных преобразований, и правил решения дробных неравенств.
2. Умножение обеих частей неравенства на неотрицательное число и дальнейшее решение полученного неравенства.
3. Возведение обеих частей в квадрат и решение полученного дробно-рационального неравенства.
Для того, чтобы рассмотреть все три способа, берем одно и тоже неравенство:
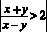
Способ № 1. Использование свойств неравенств, путем равносильных преобразований.
Равносильные переходы при решении неравенств.
Если 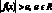
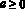
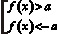
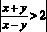
При решении воспользуемся теоремой:
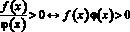
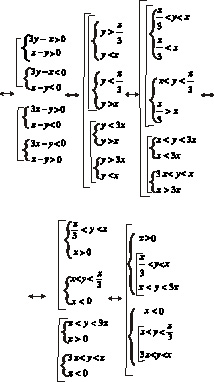
Таким образом данное неравенство равносильно совокупности неравенств:
Перенесем 2 и –2 в левую часть и приведем к общему знаменателю. (1)
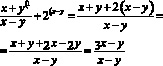
Имеем:
Воспользуемся тем, что
- произведение двух множителей < 0, если каждый множитель > 0 (или каждый < 0);
- произведение двух множителей < 0, если один из множителей < 0, а другой > 0,
и запишем данную совокупность в виде совокупности систем, применив данное чередование к каждому из неравенств. Решим данные совокупности систем неравенств:
Геометрическим решением данного неравенства являются все точки, лежащие в углах АОВ и А1ОВ1, исключая точки, расположенные на лучах ОА, ОD, ОВ и ОА1, ОС, ОВ1.
Способ №1 является наиболее универсальным при решении неравенств. Если неравенство удовлетворяет одному из равносильных переходов, то оно может быть решено данным способом.
Способ № 2. Умножение обеих частей на неотрицательное число
Так как модуль частного равен частному модулей, то:
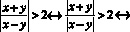
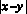
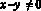
Далее для решения будем использовать метод равносильных преобразований.
Воспользуемся методом одновременного раскрытия модуля и его определением:
Решим данные неравенства:
Геометрическим решением данного неравенства являются все точки, лежащие в углах АОВ и А1ОВ1, исключая точки, расположенные на лучах ОА, ОD, ОВ и ОА1, ОС, ОВ1.
Данный способ наиболее удобен при решении дробно-рациональных неравенств.
Способ №3. Возведение обеих частей в квадрат.
Так как модуль частного равен частному модулей, то:
Так как обе части неравенства – числа неотрицательные, то равносильность не нарушается при возведении в квадрат обеих частей неравенства.
Перенесем 4 в левую сторону и приведем к общему знаменателю.
Таким образом данное неравенство равносильно системе:
Неравенство разложим на множители способом группировки.
Переходим к совокупности систем и решаем с учетом чередования знаков, как при способе равносильных преобразований.
Геометрическим решением данного неравенства являются все точки, лежащие в углах АОВ и А1ОВ1, исключая точки, расположенные на лучах ОА, ОD, ОВ и ОА1, ОС, ОВ1.
Данный способ можно использовать, если обе части неравенства есть числа неотрицательные, а возведение в квадрат не ведет к усложнению решения.
Вывод
Научная новизна исследования:
– рассмотрено три способа решения одного неравенства с двумя переменными, содержащими знак модуля;
– выведен алгоритм для каждого из трех способов решения неравенств;
– даны рекомендации по выбору способа решения;
– представлено приложение с решением неравенств различными способами.
Нужно заметить, что каждый из способов имеет свои преимущества, поэтому для успешного решения данных неравенств необходимо знать все способы. А какой из них наиболее удобный, зависит от вашего решения.
Практическая значимость исследования:
– может быть использовано учителями математики при подготовке к урокам, при изучении тем: «Координаты и графики» и «Решение неравенств», и факультативным занятиям.
– может быть использовано при проведении факультативных занятий и элективных курсов.
– для самостоятельной подготовки учащимися к ЕГЭ и вступительным экзаменам.
Рис. 1. Алгоритм решения неравенств с двумя переменными, содержащих знак модуля
Библиографическая ссылка
Дерябина А.А. НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ, СОДЕРЖАЩИЕ ЗНАК МОДУЛЯ // Международный школьный научный вестник. – 2017. – № 2.
;
URL: https://school-herald.ru/ru/article/view?id=179 (дата обращения: 26.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)