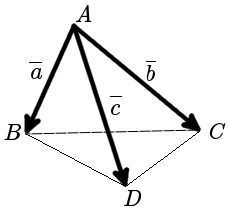
Площадь грани abcd векторах
Онлайн калькулятор. Площадь параллелограмма построенного на векторах.
Этот онлайн калькулятор позволит вам очень просто найти площадь параллелограмма построенного на векторах.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади параллелограмма построенного на векторах и закрепить пройденый материал.
Калькулятор для вычисления площади параллелограмма построенного на векторах
Выберите каким образом задается параллелограмм:
Введите значения векторов: Введите координаты трех любых вершин параллелограмма:
Инструкция использования калькулятора для вычисления площади параллелограмма построенного на векторах
Ввод данных в калькулятор для вычисления площади параллелограмма построенного на векторах
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления площади параллелограмма построенного на векторах
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Теория. Площадь параллелограмма построенного на векторах.
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
A ( ; ; ), B ( ; ; ),
C ( ; ; ), D ( ; ; )
Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Смешанное, векторное и скалярное произведение векторов
Задача:
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).
Найти:
Решение:
- а) Объем параллелепипеда будем искать через смешанное произведение векторов (AB AD AA1). Мы знаем, что модуль смешанного произведения векторов равен объему параллелепипеда, построенному на этих векторах.
| (AB AD AA1) | = |
|
= | 20 — 18 + 0 — 0 — 30 + 16 | = | -12 | . |
|---|
Мы нашли смешанное произведение, ещё надо его взять по модулю и найдём объем параллелепипеда:
VABCDA1B1C1D1=12.
б) Площадь, как мы уже знаем, можно искать через векторное произведение векторов. Грань ABCD построена на векторах AB и AD, найдём их векторное произведение. SABCD= |[AB AD]|.
| [AB AD] | = |
|
= | 6i — 8j — 2k | , |
|---|
Теперь найдём модуль этого вектора:
| SABCD= |[AB AD]|=√ | (36+64+4) | =2√(26). |
|---|
| [AD AA1] | = |
|
= | 9i — 16j — k | , |
|---|
SADD1A1= |[AD AA1]|=√(81+256+1)=13√2.
| h | = |
|
= |
|
= |
|
= |
|
. |
|---|
| cos(λ1) | = |
|
. |
|---|
Координаты вектора AB мы имеем, от вектор B1D надо найти. Для этого используем следующую формулу:
B1D = B1A1 + A1A + AD = — AB — AA1 + AD1 = — (4, 3, 0) — (-3, -2, 5) + (2, 1, 2); (Не забывайте, что всё это векторы, надо сложить их соответствующие координаты. )
Сделав вычисления по этой формуле, мы найдём, что вектор B1D имеет координаты (1, 0, -3). Теперь надо найти длину векторов AB и B1D:
|AB|=√(16+9+0)=5, |B1D|=√(1+0+9)=√(10).
Найдём скалярное произведение векторов AB и B1D, (AB B1D)=4*1 + 3*0 + 0*(-3)=4.
Теперь, имея все данные мы можем подставить их в нашу формулу:
| cos(λ1) | = |
|
= |
|
. |
|---|
д) Что бы найти cos(λ2), мы используем то, что угол между двумя плоскостями равен углу между перпендикулярами до этих плоскостей. А как мы знаем, векторное произведение — это и есть перпендикуляр до плоскости перемножаемых векторов. Поэтому в роле перпендикуляра к плоскости ADD1A1 мы можем взять вектор [AD AA1], который мы нашли в пункте б), и знаем, что его координаты (9, -16, -1), точно также и для плоскости ABCD — вектор [AB AD] с координатами (6, -8, -2).
Теперь нам остаётся, как в предыдущем варианте найти только косинус угла между двумя векторами, координаты которых нам известны.
| cos(λ2) | = |
|
= |
|
. |
|---|
Вот таким не хитрым способом мы и нашли косинус угла между гранями ABCD и ADD1A1.
Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) |
Примечание: дробные числа записывайте Округлять до -го знака после запятой. Онлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах.Этот онлайн калькулятор позволит вам очень просто найти объем пирамиды или объем тетраэдра построенных на векторах. Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление объема пирамиды построенной на векторах и закрепить пройденый материал. Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторахВыберите каким образом задается пирамида (тетраэдр): Введите значения векторов: Введите координаты вершин пирамиды: Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторахВвод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторахВ онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел. Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Теория. Объем пирамиды (объем тетраэдра) построенной на векторахОпределение Объем пирамиды (объем тетраэдра) построенной на векторах a , b и c равен шестой части модуля смешанного произведения векторов составляющих пирамиду: Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Добро пожаловать на OnlineMSchool. источники: http://mathhelpplanet.com/static.php?p=onlayn-resheniye-piramidy http://ru.onlinemschool.com/math/assistance/vector/pyramid_volume/ |
Онлайн решение Пирамиды по координатам вершин
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Аналитическая геометрия — задача на расчет пирамиды (тетраэдра)
Краткая теория
Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное — разобраться и уделить задаче достаточно времени.
Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.
Пример решения задачи
Задача
Даны координаты
вершин пирамиды
. Найти:
Сделать чертеж.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Длина ребра
Длину ребра
найдем по
формуле расстояния между 2-мя точками:
Угол между ребрами
Угол между ребрами
и
найдем как угол
между направляющими векторами
и
:
Косинус угла между
векторами:
Угол между ребром и гранью. Векторное произведение
Вычислим угол между
ребром
и гранью
.
Для этого вычислим
координаты нормального вектора плоскости
–им будет
векторное произведение векторов
и
.
Найдем векторное произведение. Для этого
вычислим определитель:
Нормальный вектор
плоскости:
Синус угла:
Площадь грани
Вычислим площадь
грани
. Она будет численно равна половине модуля векторного
произведения векторов
и
:
Искомая площадь:
Объем пирамиды. Смешанное произведение векторов
Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов
и
:
Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:
Искомый объем
пирамиды:
Уравнение прямой в пространстве
Вычислим уравнение
прямой
. Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку
Уравнение искомой
прямой:
Уравнение плоскости
Вычислим уравнение
плоскости
. Нормальный вектор плоскости
. кроме того, плоскость проходит через точку
-уравнение
грани
Уравнение высоты, опущенной на грань
Составим уравнение
высоты, опущенной на грань
из вершины
:
Нормальный вектор
является
направляющим вектором высоты, кроме того, высота проходит через точку
Искомое уравнение
высоты:
Сделаем схематический чертеж:
|
|
 |
|
||||
| Теги: векторы в пространстве, метод координат, сумма векторов, скалярное произведение векторов |
Все ответы
|
|
 |
|
|
|
 |
|
|
|
 |
|
|
|
 |
|
|
|
 |
|

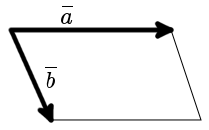
 Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).