Формулы для расчета приведены под калькулятором.
Площадь четырехугольной пирамиды
Угол наклона граней в градусах (α)
Точность вычисления
Знаков после запятой: 2
Четырехугольная пирамида
В формулах ниже будем использовать следующие обозначения:
a — длина первой стороны основания
b — длина второй стороны основания (для квадрата будет равна первой)
h — высота пирамиды
r — ребро пирамиды
d — диагональ основания
e — высота треугольника, образованного боковой гранью, т.е. высота, опущенная из вершины пирамиды на ее сторону
α — угол наклона грани пирамиды (угол между высотой треугольника боковой грани и плоскостью основания)
Во всех случаях площадь основания вычисляется тривиально — перемножением длин сторон основания. Ниже рассмотрим нахождение площадей боковых граней для разных случаев.
Площадь поверхности пирамиды через высоту
-
Находим высоту треугольника, образованного боковой гранью. Используем теорему Пифагора на прямоугольном треугольнике, образованном высотой пирамиды, высотой треугольника боковой грани, и проекцией высоты треугольника на плоскость основания. Длина проекции очевидно равна половине длины противоположной стороны. Таким образом, высота треугольника, опущенная на сторону a
высота треугольника, опущенная на сторону b
-
Находим площади боковых граней, по формуле площади равнобедренного треугольника
- Общая площадь боковых граней
Площадь поверхности пирамиды через угол наклона
Расчет через один угол наклона возможен, только если в основании пирамиды лежит квадрат (иначе пришлось бы задавать два угла). Соответственно, сторона a равна стороне b, и все грани одинаковые.
-
Находим высоту треугольника, образованного боковой гранью, поделив длину проекции на плоскость основания на косинус угла наклона
-
Находим площадь боковой грани, по формуле площади равнобедренного треугольника
- Общую площадь боковых граней получаем, умножив площадь одной грани на 4.
Площадь поверхности пирамиды через длину ребра
Здесь есть ограничение: длина ребра должна быть больше чем половина диагонали основания (иначе это не пирамида)
-
Находим высоту треугольника, образованного боковой гранью. Используем теорему Пифагора на прямоугольном треугольнике, образованном ребром пирамиды, высотой треугольника боковой грани, и половиной стороны, на которую опущена высота. Таким образом, высота треугольника, опущенная на сторону a
высота треугольника, опущенная на сторону b
-
Находим площади боковых граней, по формуле площади равнобедренного треугольника
- Общая площадь боковых граней
Площадь грани куба с учетом общей площади поверхности и площади боковой поверхности
Идти
Площадь грани куба = (Общая площадь поверхности куба—Площадь боковой поверхности куба)/2
Площадь грани куба при заданном отношении поверхности к объему
Идти
Площадь грани куба = (6/Отношение поверхности к объему куба)^(2)
Площадь грани куба при заданной площади боковой поверхности
Идти
Площадь грани куба = Площадь боковой поверхности куба/4
Площадь грани куба при заданном радиусе описанного цилиндра
Идти
Площадь грани куба = 2*Описанный цилиндр Радиус куба^2
Площадь грани куба при заданном радиусе вписанного цилиндра
Идти
Площадь грани куба = 4*Вписанный цилиндр Радиус куба^2
Площадь грани куба при заданной общей площади поверхности
Идти
Площадь грани куба = Общая площадь поверхности куба/6
Площадь грани куба с учетом пространственной диагонали
Идти
Площадь грани куба = Космическая диагональ куба^(2)/3
Площадь грани куба с учетом радиуса средней сферы
Идти
Площадь грани куба = 2*Радиус средней сферы куба^2
Площадь грани куба с учетом радиуса окружности
Идти
Площадь грани куба = 4/3*Окружность Радиус куба^2
Площадь грани куба по периметру грани
Идти
Площадь грани куба = Лицевой периметр куба^(2)/16
Площадь грани куба по диагонали грани
Идти
Площадь грани куба = Диагональ грани куба^(2)/2
Площадь грани куба с заданным радиусом Insphere
Идти
Площадь грани куба = 4*Insphere Радиус куба^2
Площадь грани куба по периметру
Идти
Площадь грани куба = (Периметр куба/12)^(2)
Площадь грани куба
Идти
Площадь грани куба = Длина ребра куба^(2)
Площадь грани куба при заданном объеме
Идти
Площадь грани куба = Объем куба^(2/3)
Площадь боковой поверхности куба при заданной общей площади поверхности и длине ребра
Идти
Площадь боковой поверхности куба = Общая площадь поверхности куба-2*Длина ребра куба^2
Общая площадь поверхности куба при заданной площади боковой поверхности
Идти
Общая площадь поверхности куба = 3/2*Площадь боковой поверхности куба
Общая площадь поверхности куба с учетом пространственной диагонали
Идти
Общая площадь поверхности куба = 2*Космическая диагональ куба^2
Площадь боковой поверхности куба
Идти
Площадь боковой поверхности куба = 4*Длина ребра куба^2
Площадь боковой поверхности куба при заданном объеме
Идти
Площадь боковой поверхности куба = 4*Объем куба^(2/3)
Общая площадь поверхности куба
Идти
Общая площадь поверхности куба = 6*Длина ребра куба^2
Общая площадь поверхности куба при заданном объеме
Идти
Общая площадь поверхности куба = 6*Объем куба^(2/3)
Площадь грани куба с учетом радиуса окружности
Идти
Площадь грани куба = 4/3*Окружность Радиус куба^2
Площадь грани куба по периметру
Идти
Площадь грани куба = (Периметр куба/12)^(2)
Площадь грани куба
Идти
Площадь грани куба = Длина ребра куба^(2)
Как найти площадь поверхности пирамиды
На данной странице калькулятор поможет рассчитать площадь поверхности пирамиды онлайн. Для расчета задайте площадь основания и апофему.
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса. Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.
Апофема – опущенный перпендикуляр из вершины на ребро основания.
Боковая поверхность через периметр и апофему
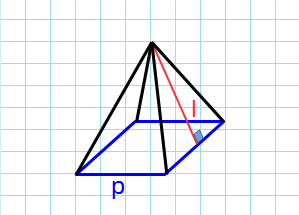
Формула площади боковой поверхности правильной пирамиды через периметр и апофему:
p — периметр основания пирамиды; l — апофема пирамиды.
Боковая поверхность через высоту и сторону основания
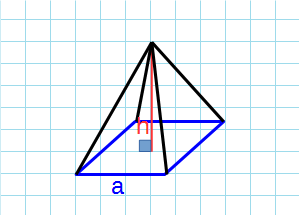
Формула площади боковой поверхности правильной пирамиды через высоту и сторону основания:
a — сторона основания; h — высота пирамиды; n — число сторон в основании.
Полная поверхность через высоту и сторону основания

Формула площади полной поверхности правильной пирамиды через высоту и сторону основания:
a — сторона основания; h — высота пирамиды; n — число сторон в основании.
Полная площадь тетраэдра
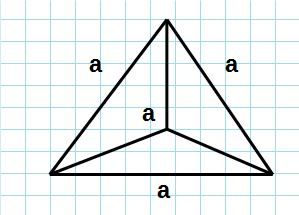
Формула полной площадь тетраэдра:
a — сторона основания.
© 2011-2023 Довжик Михаил
Копирование материалов запрещено.
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com
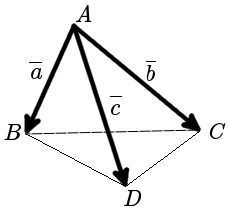
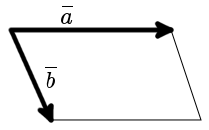
Площадь грани abcd векторах
Онлайн калькулятор. Площадь параллелограмма построенного на векторах.
Этот онлайн калькулятор позволит вам очень просто найти площадь параллелограмма построенного на векторах.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади параллелограмма построенного на векторах и закрепить пройденый материал.
Калькулятор для вычисления площади параллелограмма построенного на векторах
Выберите каким образом задается параллелограмм:
Введите значения векторов: Введите координаты трех любых вершин параллелограмма:
Инструкция использования калькулятора для вычисления площади параллелограмма построенного на векторах
Ввод данных в калькулятор для вычисления площади параллелограмма построенного на векторах
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления площади параллелограмма построенного на векторах
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Теория. Площадь параллелограмма построенного на векторах.
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
A ( ; ; ), B ( ; ; ),
C ( ; ; ), D ( ; ; )
Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Смешанное, векторное и скалярное произведение векторов
Задача:
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).
Найти:
Решение:
- а) Объем параллелепипеда будем искать через смешанное произведение векторов (AB AD AA1). Мы знаем, что модуль смешанного произведения векторов равен объему параллелепипеда, построенному на этих векторах.
| (AB AD AA1) | = |
|
= | 20 — 18 + 0 — 0 — 30 + 16 | = | -12 | . |
|---|
Мы нашли смешанное произведение, ещё надо его взять по модулю и найдём объем параллелепипеда:
VABCDA1B1C1D1=12.
б) Площадь, как мы уже знаем, можно искать через векторное произведение векторов. Грань ABCD построена на векторах AB и AD, найдём их векторное произведение. SABCD= |[AB AD]|.
| [AB AD] | = |
|
= | 6i — 8j — 2k | , |
|---|
Теперь найдём модуль этого вектора:
| SABCD= |[AB AD]|=√ | (36+64+4) | =2√(26). |
|---|
| [AD AA1] | = |
|
= | 9i — 16j — k | , |
|---|
SADD1A1= |[AD AA1]|=√(81+256+1)=13√2.
| h | = |
|
= |
|
= |
|
= |
|
. |
|---|
| cos(λ1) | = |
|
. |
|---|
Координаты вектора AB мы имеем, от вектор B1D надо найти. Для этого используем следующую формулу:
B1D = B1A1 + A1A + AD = — AB — AA1 + AD1 = — (4, 3, 0) — (-3, -2, 5) + (2, 1, 2); (Не забывайте, что всё это векторы, надо сложить их соответствующие координаты. )
Сделав вычисления по этой формуле, мы найдём, что вектор B1D имеет координаты (1, 0, -3). Теперь надо найти длину векторов AB и B1D:
|AB|=√(16+9+0)=5, |B1D|=√(1+0+9)=√(10).
Найдём скалярное произведение векторов AB и B1D, (AB B1D)=4*1 + 3*0 + 0*(-3)=4.
Теперь, имея все данные мы можем подставить их в нашу формулу:
| cos(λ1) | = |
|
= |
|
. |
|---|
д) Что бы найти cos(λ2), мы используем то, что угол между двумя плоскостями равен углу между перпендикулярами до этих плоскостей. А как мы знаем, векторное произведение — это и есть перпендикуляр до плоскости перемножаемых векторов. Поэтому в роле перпендикуляра к плоскости ADD1A1 мы можем взять вектор [AD AA1], который мы нашли в пункте б), и знаем, что его координаты (9, -16, -1), точно также и для плоскости ABCD — вектор [AB AD] с координатами (6, -8, -2).
Теперь нам остаётся, как в предыдущем варианте найти только косинус угла между двумя векторами, координаты которых нам известны.
| cos(λ2) | = |
|
= |
|
. |
|---|
Вот таким не хитрым способом мы и нашли косинус угла между гранями ABCD и ADD1A1.
Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) |
Примечание: дробные числа записывайте Округлять до -го знака после запятой. Онлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах.Этот онлайн калькулятор позволит вам очень просто найти объем пирамиды или объем тетраэдра построенных на векторах. Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление объема пирамиды построенной на векторах и закрепить пройденый материал. Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторахВыберите каким образом задается пирамида (тетраэдр): Введите значения векторов: Введите координаты вершин пирамиды: Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторахВвод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторахВ онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел. Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Теория. Объем пирамиды (объем тетраэдра) построенной на векторахОпределение Объем пирамиды (объем тетраэдра) построенной на векторах a , b и c равен шестой части модуля смешанного произведения векторов составляющих пирамиду: Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Добро пожаловать на OnlineMSchool. источники: http://mathhelpplanet.com/static.php?p=onlayn-resheniye-piramidy http://ru.onlinemschool.com/math/assistance/vector/pyramid_volume/ |

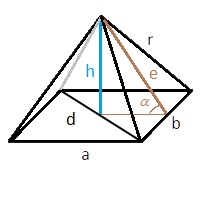
 Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).