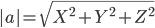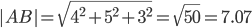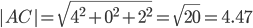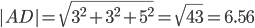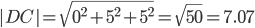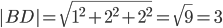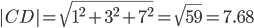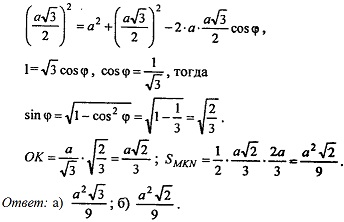Площадь грани пирамиды
1) Координаты векторов
Координаты векторов находим по формуле:
X = xj — xi; Y = yj — yi; Z = zj — zi
здесь X,Y,Z координаты вектора; xi, yi, zi — координаты точки Аi; xj, yj, zj — координаты точки Аj;
Например, для вектора AB
X = x2 — x1; Y = y2 — y1; Z = z2 — z1
X = -1-3; Y = 6-1; Z = 1-4
AB(-4;5;-3), AC(-4;0;2), AD(-3;3;-5), BC(0;-5;5), BD(1;-2;-2), CD(1;3;-7)
2) Модули векторов
Длина вектора a(X;Y;Z) выражается через его координаты формулой: 
4) Площадь грани
Площадь грани можно найти по формуле:
S=½·|a|·|b|·sin γ
Найдем площадь грани ABC
Найдем угол между ребрами AB и AC:
Площадь грани ABC
Найдем площадь грани ABD
Найдем угол между ребрами AB и AD:
Площадь грани ABD
Найдем площадь грани ACD
Найдем угол между ребрами AC и AD:
Площадь грани ACD
Найдем площадь грани BCD
Найдем угол между ребрами BC и BD:
Площадь грани BCD
7) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:
Уравнение прямой AB
Уравнение прямой AC
Уравнение прямой BC
Уравнение прямой BD
Уравнение прямой CD
Уравнение плоскости
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
Уравнение плоскости ABC
(x-3)(5·2-0·(-3)) — (y-1)((-4)·2-(-4)·(-3)) + (z-4)((-4)·0-(-4)·5) = 10x + 20y + 20z + 130 = 0
Уравнение плоскости ABD
(x-3)(5·(-5)-3·(-3)) — (y-1)((-4)·(-5)-(-3)·(-3)) + (z-4)((-4)·3-(-3)·5) = -16x — 11y + 3z-47 = 0
Уравнение плоскости ACD
(x-3)(0·(-5)-3·2) — (y-1)((-4)·(-5)-(-3)·2) + (z-4)((-4)·3-(-3)·0) = -6x — 26y — 12z-92 = 0
Уравнение плоскости BCD
(x+1)((-5)·(-2)-(-2)·5) — (y-6)(0·(-2)-1·5) + (z-1)(0·(-2)-1·(-5)) = 20x + 5y + 5z + 15 = 0
9) Уравнение плоскости, проходящей через точку перпендикулярно вектору
Уравнение плоскости, проходящей через точку M0(x0, y0, z0) перпендикулярно вектору N = (l,m,n), имеет вид:
l(x- x0) + m(y- y0) + n(z- z0) = 0
-4(x — (-1)) + 5(y — 1) + (-3)(z — 6) = 0
-4x + 5y -3z + 9 = 0
10) Длина высоты пирамиды, проведенной из вершины A
Расстояние d от точки M1(x1;y1;z1) до плоскости Ax + By + Cz + D = 0 равно абсолютному значению величины:
11) Уравнение высоты пирамиды через вершину A
Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
12) Угол между прямой AB и плоскостью ABC
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле
13) Угол между плоскостью ABC и плоскостью ABD
Косинус угла между плоскостью A1x + B1y + C1 + D = 0 и плоскостью A2x + B2y + C2 + D = 0 равен углу между их нормальными векторами N1(A1, B1, C1) и N2(A2, B2, C2):
Вычисление площади правильной треугольной пирамиды
Правильная треугольная пирамида (тетраэдр) — это многогранник, в основании которого лежит правильный треугольник со сторонами a и боковыми гранями в виде равнобедренных треугольников с основанием a и сторонами b.
Площадь поверхности такой фигуры складывается из площадей основания многогранника и трех боковых граней. В записи на математический язык это выглядит так:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Нахождение площади основания пирамиды
Поскольку правильный тетраэдр основан на треугольнике, для определения площади основания рассматриваемого многогранника воспользуемся формулой нахождения площади треугольника:
Значение переменных: a — длина стороны равностороннего треугольника, h — его высота.
Далее произведем подстановку формулы вычисления высоты правильного треугольника и получим искомое выражение:
Вычисление площади боковых граней и полной поверхности
Боковые грани правильной треугольной пирамиды представлены тремя равнобедренными треугольниками. Выведем формулу расчета площади каждого из них из классического способа вычисления площади треугольника:
Здесь переменная a обозначает основание треугольника, h — его высоту.
Теперь выполним подстановку выражения, с помощью которого находится высота треугольника с одинаковыми бедрами, и получим уравнение определения площади равнобедренного треугольника:
В этом случае b — это боковые ребра треугольника, равные между собой.
Подставим в выражение (1) формулы (2) и (3) и получим уравнение, с помощью которого рассчитывается площадь полной поверхности правильного тетраэдра:
Примеры задач с решением
Задача
Дано
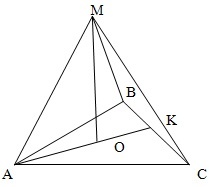
Правильный тетраэдр MABC с вершиной М. Высота основания AK=3 см.
∠MAB=∠MAC=∠MBA=∠MBC=∠MAB=∠MCA=∠MCB=45°. Необходимо вычислить площадь пирамиды MABC.
Решение
В основании правильного тетраэдра лежит равносторонний треугольник с известной длиной высоты. Применим свойство правильного треугольника, состоящее в следующем:
Преобразуем данное выражение так, чтобы вывести формулу стороны a:
Теперь найдем a:
Подставим полученное выражение в формулу нахождения площади основания правильного многогранника с тремя боковыми гранями:
Далее необходимо найти площадь боковых граней тетраэдра. Для этого произведем вычисление высоты MK. Так как угол между гранью и основанием пирамиды равен 45°, то ∠OKM=45°, следовательно:
По свойству правильного треугольника, отрезок OK равен радиусу вписанной в ΔABC окружности.
Найдем ее по соответствующей формуле:
Подставим найденную величину в отношение ОК к МК:
Из данной пропорции выведем выражение, по которому можно определить длину высоты MK:
Теперь, когда известны основание и высота равнобедренного треугольника, составляющего боковую грань пирамиды MABC, подставим значения в классическую формулу нахождения площади треугольника:
Как найти площадь грани в пирамиде
Площадь боковой поверхности и основания, периметр основания пирамиды и ее объем связывают между собой определенные формулы. Это порой дает возможность вычислить значения недостающих данных, необходимых для определения площади грани в пирамиде.
Объем любой не усеченной пирамиды равен трети от произведения высоты пирамиды и площади основания. Для правильной пирамиды справедливо: площадь боковой поверхности равна половине периметра основания умноженного на высоту одной из граней. При расчете объема усеченной пирамиды, вместо площади основания подставляется величина, равная сумме площадей верхнего, нижнего основания и квадратного корня из их произведения.
- Стереометрия
- как найти боковую грань пирамиды
- Как найти площадь боковой поверхности пирамиды
- Как найти площадь оснований пирамиды
- Как найти площадь тетраэдра
я могу помочь с этим заданием
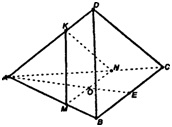
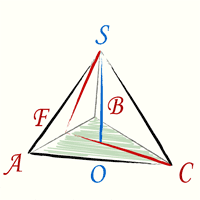
а) Пусть т. О — центр грани АВС. Построим МК || DB, MN || ВС.
пл .MKN — искомое сечение.
Пусть ребро тетраэдра равно а. Тогда 
Т.к. ΔADB — равносторонний, а КМ || DB, то ΔАМК — также равносторонний, АМ=КМ=
(углы с соответственно параллельными и одинаково направленными сторонами):
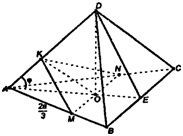
б) Построим отрезок 
в пл. ADO. Т.к. пл.
то 
Т.к. 
и 
то 
Значит, ΔKMN — искомое сечение, 
ΔAMN — равносторонний, MN = AM =
Из ΔADE по теореме косинусов имеем:
DE2 = AD2 + АЕ2 — 2 ∙ AD ∙ АЕ ∙ cos φ,
Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) |
Примечание: дробные числа записывайте Округлять до -го знака после запятой. Что такое тетраэдр: определение, виды, формулы площади и объемаВ данной публикации мы рассмотрим определение и разновидности тетраэдра, а также формулы для расчета площади его поверхности (одной грани и полной) и объема. Представленная информация сопровождается наглядными рисунками для лучшего восприятия. Определение тетраэдраТетраэдр – это разновидность пирамиды; четырехгранник, гранями которого являются треугольники.
Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Каждая грань фигуры может быть ее основанием. Развертка тетраэдра на примере правильной фигуры представлена ниже:
Основные элементы и свойства тетраэдра (к нему применимы свойства правильной пирамиды) мы рассмотрели в отдельной публикации. Как найти высоту тетраэдра формула
Высота тетраэдра — равна корню квадратному из двух третих, помноженному на длину ребра тетраэдра (h – высота тетраэдра, a – ребро тетраэдра) |
Вывод формулы высоты тетраэдра
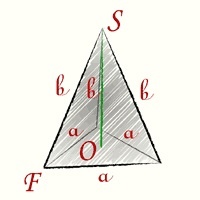
Чтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS:
Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1).
Рассмотрим произвольный треугольник ABC и точку D , не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC . В результате получим треугольники ADC , CDB , ABD . Поверхность ограниченная четырьмя треугольниками ABC , ADC , CDB и ABD называется тетраэдром и обозначается DABC . 
Треугольники, из которых состоит тетраэдр, называются его гранями.
Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра
Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.
Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.
Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.
Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле
- S – площадь любой грани,
- H – высота, опущенная на эту грань
Правильный тетраэдр – частный вид тетраэдра
Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:
- Все грани равны.
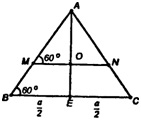
- Все плоские углы правильного тетраэдра равны 60°
- Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
- Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).
Пусть нам дан правильный тетраэдр ABCD с ребрами равными a . DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD .
Высота BM равна BM и равна 
Рассмотрим треугольник BDM , где DH , являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой
, где
BM=, DM=, BD=a,
p=1/2 (BM+BD+DM)= 
Подставим эти значения в формулу высоты. Получим
Вынесем 1/2a. Получим
Применим формулу разность квадратов
После небольших преобразований получим
Объем любого тетраэдра можно рассчитать по формуле 
,
где 
,
Подставив эти значения, получим 
Таким образом формула объема для правильного тетраэдра
где a –ребро тетраэдра
Вычисление объема тетраэдра, если известны координаты его вершин
Пусть нам даны координаты вершин тетраэдра
Из вершины 
проведем векторы 
, 
, 
.
Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим
Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула
Свойства
Зная высоту тетраэдра, можно вычислить его ребро, перевернув формулу так, чтобы ребро было равно корню из трех вторых, умноженному на высоту. a=√(3/2) h
Выразив таким образом ребро тетраэдра через его высоту, можно найти периметр тетраэдра, то есть длину всех его ребер, площадь одной грани и площадь полной поверхности тетраэдра. Периметр тетраэдра будет равен шести длинам его ребер, площадь одной грани – ребру в квадрате, умноженному на корень из трех, деленный на четыре, а площадь полной поверхности – четырем площадям одной грани. P=6a=6√(3/2) h S_1=(√3 a^2)/4=(3√3 h^2)/8 S_(п.п.)=4S_1=(3√3 h^2)/2
Через высоту, подставленную вместо ребра в определенном соотношении можно найти соответственно и радиусы вписанной и описанной окружностей в основание тетраэдра. r=h/(2√2) R=h/√2
Апофема тетраэдра проходит из вершины к противоположной стороне грани под прямым углом и рассчитать ее можно как из прямоугольного треугольника с боковым ребром по той же грани, так и из прямоугольного треугольника во внутреннем пространстве тетраэдра с высотой. l=3h/(2√2)
Чтобы вычислить объем тетраэдра, необходимо возвести в куб ребро и разделить полученное значение на шесть корней из двух, либо подставить вместо ребра корень из трех вторых, умноженный на высоту и преобразовать формулу объема для высоты. V=(√3 h^3)/8
В тетраэдр можно вписать сферу или описать сферу около него, тогда, зная высоту, чтобы вычислить радиусы вписанной и описанной сфер, необходимо воспользоваться следующими, уже готовыми формулами. (рис.60.2, 60.3) r_1=h/4 R_1=3h/4
Что такое тетраэдр: определение, виды, формулы площади и объема
http://planshet-info.ru/kompjutery/kak-najti-vysotu-tetrajedra-formula
В данной публикации мы рассмотрим определение и разновидности тетраэдра, а также формулы для расчета площади его поверхности (одной грани и полной) и объема. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
- Определение тетраэдра
- Виды тетраэдра
- Формулы площади и объема правильного тетраэдра
Определение тетраэдра
Тетраэдр – это разновидность пирамиды; четырехгранник, гранями которого являются треугольники.
Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Каждая грань фигуры может быть ее основанием.
Развертка тетраэдра на примере правильной фигуры представлена ниже:
Основные элементы и свойства тетраэдра (к нему применимы свойства правильной пирамиды) мы рассмотрели в отдельной публикации.
Виды тетраэдра
- Равногранный тетраэдр – боковые грани фигуры равны, а основанием является правильный (равносторонний) треугольник.
- Прямоугольный тетраэдр – угол между всеми тремя ребрами при одной вершине является прямым, т.е. равным 90°.
- Правильный тетраэдр – все ребра равны, а грани, соответственно, являются равносторонними треугольниками.
- Ортоцентричный тетраэдр – все высоты, проведенные из всех вершин фигуры к противолежащим граням, пересекаются в одной точке.
Формулы площади и объема правильного тетраэдра
Площадь поверхности
Объем
