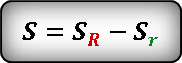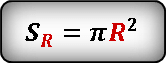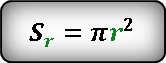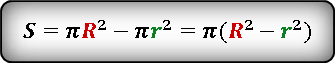Как найти площадь кольца если известен радиус - Исправление недочетов и поиск решений вместе с Examum.ru

Площадь кольца

Главная
/
Математика
/
Геометрия
/
Площадь кольца

Чтобы найти площадь кольца, ограниченного двумя концентрическими окружностями, воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Площадь кольца по радиусам или диаметрам

Чему равна площадь кольца ограниченного двумя окружностями, если:

у внешней окружности

у внутренней окружности

Ответ: S =

Округление числа π: Округление ответа:

Просто введите радиусы или диаметры окружностей, и получите ответ.

Площадь кольца по толщине и любому другому параметру

Чему равна площадь кольца ограниченного двумя окружностями, если:

толщина кольца t =

Ответ: S =

Округление числа π: Округление ответа:

Просто введите толщину кольца и любой другой известный вам параметр, и получите ответ.

Теория

Площадь кольца через радиусы

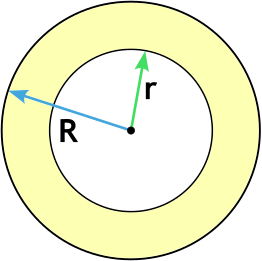
Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?

Формула

S = π ⋅ (R² — r²)

Пример

К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:

S = 3.14 ⋅ (3² — 2²) = 3.14 ⋅ (9 — 4) = 3.14 ⋅ 5 = 15.7 см²

Ответ: S = 15.7 см²

Площадь кольца через диаметры

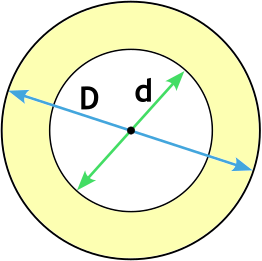
Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?

Формула

S = ^π/₄ ⋅ (D² — d²)

Пример

К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:

S = 3.14 / 4 ⋅ (4² — 2²) = 0.785 ⋅ (16 — 4) = 9.42 см²

Ответ: S = 9.42 см²

Площадь кольца через толщину

Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:

внешний диаметр D
внутренний диаметр d
радиус внешней окружности R
радиус внутренней окружности r

Формулы

S = ^π/₄ ⋅ (D² — (D — 2t)²)

S = ^π/₄ ⋅ ((d + 2t)² — d²)

S = π ⋅ (R² — (R — t)²)

S = π ⋅ ((r + t)² — r²)

Пример

Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:

S = 3.14/4 ⋅ (5² — (5 — 2 ⋅ 2)²) = 0.785 ⋅ (25 — 1) = 18.84 см²

См. также

Источник

{S = pi (R^2 — r^2)}

С помощью приведенных калькулятора и формул можно рассчитать площадь кольца через радиусы или диаметры онлайн.

Кольцо — плоская геометрическая фигура, ограниченная двумя концентрическими окружностями.

Содержание:

калькулятор площади кольца
формула площади кольца через радиусы
формула площади кольца через диаметры
примеры задач

Формула площади кольца через радиусы

{S = pi (R^2 — r^2)}

R — внешний радиус кольца

r — внутренний радиус кольца

Формула площади кольца через диаметры

{S= dfrac{pi}{4}(D^2 — d^2)}

D — внешний диаметр кольца

d — внутренний диаметр кольца

Примеры задач на нахождение площади кольца

Задача 1

Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 3 см и 7 см.

Решение

В условии задачи даны радиусы ограничивающих кольцо окружностей, поэтому воспользуемся первой формулой.

S = pi (R^2 — r^2) = pi (7^2 — 3^2) = pi (49 — 9) = 40pi approx 125.66371 : см^2

Ответ: 108 cdot 0.866 approx 93.53074 : см^2

Полученный ответ можно проверить с помощью калькулятора .

Задача 2

Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны dfrac{4}{sqrt{pi}} и dfrac{2}{sqrt{pi}}.

Решение

Задача похожа на предыдущую, поэтому алгоритм ее решения будет тот же.

S = pi (R^2 — r^2) = pi ({Big(dfrac{4}{sqrt{pi}} Big) }^2 — {Big(dfrac{2}{sqrt{pi}} Big) }^2) = pi (dfrac{16}{pi} — dfrac{4}{pi}) = pi dfrac{12}{pi} = 12 : см^2

Ответ: 12 : см^2

Наш калькулятор может производить вычисления с выражениями. Для того, чтобы ввести радиусы из условия их нужно записать в понятном для калькулятора формате:

dfrac{4}{sqrt{pi}} : rarr : 4/sqrt(pi)

dfrac{2}{sqrt{pi}} : rarr : 2/sqrt(pi)

Если ввести данные в таком формате, можно проверить ответ .

Задача 3

Найдите площадь кольца образованного двумя окружностями с общим центром если радиусы равны 15 и 13.

Решение

Задача аналогична предыдущим.

S = pi (R^2 — r^2) = pi (15^2 — 13^2) = pi (225 — 169) = 56pi approx 175.92919 : см^2

Ответ: 56pi approx 175.92919 : см^2

Проверка .

Задача 4

Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 13 и 12 см.

Решение

Задача аналогична предыдущим.

S = pi (R^2 — r^2) = pi (13^2 — 12^2) = pi (169 — 144) = 25pi approx 78.53982 : см^2

Ответ: 25pi approx 78.53982 : см^2

Проверка .

Источник

Кольцо – это плоская геометрическая фигура, которая представляет собой часть плоскости между двумя окружностями с общим центром, но имеющими разный радиус.

Площадь кольца, выраженная через внешний и внутренний радиусы

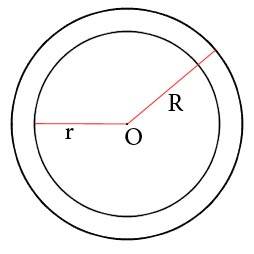
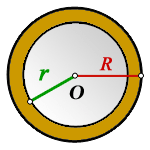
Пусть дана окружность радиуса R и окружности радиуса r. Причем R>r. Совместим центры этих окружностей. Фигура, заключенная между этими окружностями и будет кольцо, у которого R является внешним радиусом, r -внутренним радиусом.
Тогда площадь этой фигуры будет равна разницы между площадью круга с большим радиусом и площадью круга с меньшим радиусом.

Площадь круга с радиусом r выражается формулой:
$S={pi}r^2$
Площадь круга с радиусом R выражается формулой:
$S={pi}R^2$
Тогда площадь кольца будет равна:

$S={pi}R^2-{pi}r^2={pi}(R^2-r^2)$

Таким образом, площадь кольца равна произведению числа на разницу квадратов внешнего и внутреннего радиусов: $S={pi}(R^2-r^2)$

Пример расчета площади кольца, если известны его радиусы.
Найдите площадь кольца, если его внешний радиус равен 3, а внутренний – 2
Площадь кольца вычисляется по формуле:
$S={pi}(R^2-r^2)$
Подставив значения из условия задачи, имеем:
$S={pi}(3^2-2^2)=5{pi}$

Площадь кольца, выраженная через внешний и внутренний диаметры

Иногда при решении задач удобней использовать формулу площади кольца, выраженную через внутренний и внешний диаметры.

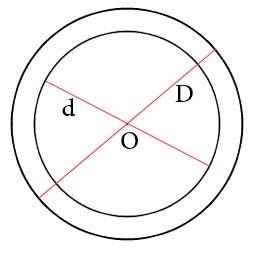
Пусть D – внешний диаметр кольца, d -внутренний диаметр кольца, тогда:

Выразим радиус через диаметр. Имеем:

Площадь кольца вычисляется по формуле:
$S={pi}(R^2-r^2)$
Подставив выраженные через диаметр радиусы, получим:
$S={pi}(({1/2}D)^2-({1/2}d)^2 )={pi} {1/4}(D^2-d^2)$
Таким образом, площадь кольца равна четверти произведения числа на разницу квадратов внешнего и внутреннего диаметров:
$S={{pi}/4}(D^2-d^2)$

Пример расчета площади кольца, если известны его диаметры.
Найдите площадь кольца, если его внешний диаметр равен 10, а внутренний – 6
Площадь кольца вычисляется по формуле:
$S={{pi}/4}(D^2-d^2)$
Подставив значения из условия задачи, имеем:
$S={{pi}/4 }{({10}^2-6^2)}=16{pi}$

Площади кольца, выраженная через средний радиус и ширину кольца

Пусть k– ширина кольца, являющийся разницей между большим и меньшим радиусом, то есть k=R-r-средний радиус кольца, равный

Площадь кольца вычисляется по формуле:
$S={pi}(R^2-r^2)$
Применив формулу разности квадратов, имеем:
$S={pi}(R^2-r^2 )={pi}(R-r)(R+r)$
Но R-r=k, а
Подставим правые части равенства в формулу площади кольца.
Получим:

Площадь кольца равна удвоенному произведению числа среднего радиуса на ширину кольца.

Пример расчета площади кольца, если известны его средний радиус и ширина.
Найдите площадь кольца, если его средний радиус равен 5, а ширина – 2

Площадь кольца вычисляется по формуле:

Подставив значения из условия задачи, имеем:

Площади кольца через длину самого большого отрезка, проведенного внутри кольца

Пусть AB –самый большой отрезок, лежащий внутри кольца. Точка С – половина этого отрезка. Этот отрезок будет являться касательной к кругу меньшего радиуса. Касательная перпендикулярна радиусу меньшей окружности, проведенного в точку каcания C. Тогда
Следовательно, треугольник ACO –прямоугольный, где

По теореме Пифагора имеем:
${AO}^2={AC}^2+{CO}^2$
$R^2=({1/2} AB)^2+r^2$
$R^2-r^2=({1/2} AB)^2$
Площадь кольца равна:
$S={pi}(R^2-r^2)$
Подставив, получим:
$S={pi}({1/2} AB)^2$
Следовательно, площадь кольца равна произведению числа на квадрат половины самого большого отрезка кольца.

Источник

При помощи нашего калькулятора вы легко сможете узнать площадь кольца.

Для того что бы вычислить площадь кольца необходимо знать его внутренний и внешний радиус или внутренний и внешний диаметр. Если нам известны указанные величины, для нас не составит труда вычислить площадь кольца.
Площадь кольца рассчитывается по следующим формулам:

Если нам известен радиус:
Формула для расчета площади кольца через радиус:
S=π(R²-r²)
Если нам известен диаметр:
Формула для расчета площади кольца через диаметр:
S=π/4(D²-d²)

Где S – площадь кольца, R — внешний радиус кольца, r – внутренний радиус кольца, D – внешний диаметр кольца, d — внутренний диаметр кольца, π – число Пи которое всегда примерно равно 3,14.

Источник

Условие задачи:

Две окружности, имеющие общий центр, образуют кольцо. Радиус внешней окружности равен 10 см, а внутренней 8 см. Найти площадь этого кольца.

Дано:
Радиус внешней окружности, R = 10 см
Радиус внутренней окружности, r = 8 см

Пояснение к рисунку:
O — общий центр окружностей

Найти площадь кольца: S

Решение

Площадь кольца можно выразить как разницу между площадями внешнего круга и внутреннего.

Формула площади внешнего круга.

Формула площади внутреннего круга.

После подстановки и преобразования, получаем следующее выражение для площади кольца.

Вставляем значения.

Ответ:

Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14

Калькулятор для расчета площади кольца

Подробности

Опубликовано: 06 сентября 2017

Обновлено: 13 августа 2021

Источник