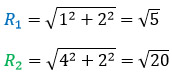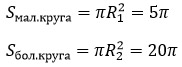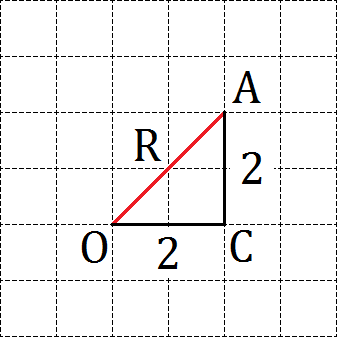Решение:
Окружности нарисованы не очень удачно потому, что мы не можем с точностью сказать, какова длина у их радиусов. Придется искать.
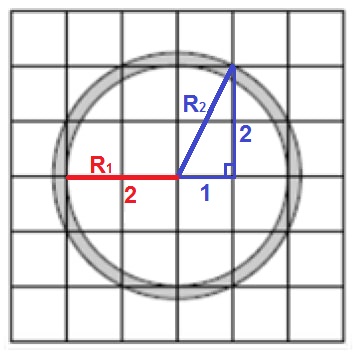
Начертим радиусы этих двух окружностей так, как показано на рисунке, а затем сделаем еще одно дополнительное построение: достроим эти радиусы до прямоугольных треугольников.
Теперь с помощью теоремы Пифагора можно найти длины радиусов.
Далее найдем площадь маленького круга с радиусом R1 и большого круга с радиусом R2.
Чтобы найти площадь кольца надо из площади большого круга вычесть площадь маленького:
В ответе нас просят записать площадь, деленную на π, т.е. просто 15.
Ответ: 15.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
#799
3 октября 2013
Сегодня мы разберем нестандартную задачу B5 на площади из ЕГЭ по математике. В этой задаче требуется найти площадь закрашенного кольца, которое представляет собой две концентрические окружности разных радиусов:
Задача. Найдите площадь S закрашенного кольца, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S/π.

Как и во всех задачах, для решения нам потребуется формула площади круга:
S = πR2
где R — радиус круга. Это стандартная формула, и ее обязательно надо знать. Но поскольку в задаче фигурируют два круга, то и радиусов будет два. Обозначим внутренний радиус (меньшей окружности) буквой R1, а внешний радиус — R2. Внутренний радиус очень легко считается, он равен двум клеточкам:
R1 = 2 ⇒ R12 = 4
Со вторым радиусом все сложнее. Окружность не проходит через «классические» точки горизонтальной и вертикальной осей, по которым обычно измеряется радиус. Однако на этой окружности есть другие точки, которые лежат в узлах исходной сетки. Отметим эти точки красным:
Что дают нам эти точки? Как минимум — визуальное представление того, как выглядит радиус. Для того, чтобы его вычислить, давайте отдельную сетку, на которой отметим центр окружности O и ту точку A на нашей окружности, в которую мы провели радиус. Затем достроим полученный отрезок до прямоугольного треугольника, двигаясь вдоль линий сетки. Получим треугольник OAC с прямым углом C:
По теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов) получаем:
R2 = OA2 = OC2 + AC2 = 22 + 22 = 4 + 4 = 8
Итого мы получили:
R22 = 8
Теперь осталось найти площади внешнего и внутреннего кругов, образующих кольцо:
S1 = πR12 = π · 4 = 4π;
S2 = πR22 = π · 8 = 8π.
Поскольку закрашенное кольцо лежит между границами кругов, для нахождения его площади надо из площади большего круга S2 вычесть площадь меньшего круга S1. Получаем:
S = S2 − S1 = 8π − 4π = 4π
Но это еще не ответ! В задаче требуется найти величину S/π. Давайте сосчитаем:
S/π = 4π/π = 4
Вот мы и получили ответ! Как видите, ничего сверхъестественного в этой задаче нет. Достаточно помнить формулу площади круга, а также находить эту площадь через радиус, даже если этот радиус приходится считать через теорему Пифагора.
Надеюсь, этот урок сильно поможет тем, кто всерьез готовится к ЕГЭ по математике. Тем, кто не рассчитывает на то, что им попадутся легкие задачи (в частности, задача B5), а готовится решать в том числе и нестандартные примеры. В общем тренируйтесь — и обязательно сдадите экзамен на отличный балл.:)
Смотрите также:
- Нестандартная задача B5 на площадь круга
- Задача B5: площадь закрашенного сектора
- Десятичные дроби
- Специфика работы с логарифмами в задаче B15
- Семинар: ЕГЭ по математике, задачи B3 на площади
- Решение задач на движение по воде
Всем известно, что площадь круга высчитывают по формуле S=πR²
То есть всегда необходимо знать радиус, чтобы найти площадь.
Судя по условию задания и по рисунку,
радиус большого круга — 2 см, а радиус внутреннего — 1 см, а постоянное число π = 3,14.
Высчитываем площадь большого круга
S = 3,14 х 2 х 2 = 12,56.
Площадь внутреннего круга
S = 3,14 х 1 х 1 = 3, 14.
Площадь кольца можно найти вычитанием и площади большого круга площадь внутреннего.
12,56 — 3,14 = 9,42.
Если выяснять, сколько это частей π, непонятно только, зачем?
9,42 : 3, 14 = 3.
Задания
Версия для печати и копирования в MS Word
На клетчатой бумаге с размером клетки 1 см 1 см изображено кольцо. Найдите его площадь. В ответ запишите площадь, делённую на
Ответ дайте в квадратных сантиметрах.
Решение.
Это задание ещё не решено, приводим решение прототипа.
На клетчатой бумаге с размером клетки 1 см 1 см изображено кольцо. Найдите его площадь. В ответ запишите площадь, делённую на
Ответ дайте в квадратных сантиметрах.
Площадь кольца равна разности площади большого и малого кругов. Радиус большого круга равен 2, а малого — 1, откуда
Поэтому
Ответ: 3.
Кодификатор ФИПИ/Решу ЕГЭ:
1
2
3
4
На клетчатой бумаге с размером клетки 1 см 1 см изображено кольцо. Найдите его площадь. В ответ запишите площадь, делённую на
Ответ дайте в квадратных сантиметрах.
5
На клетчатой бумаге с размером клетки 1 см 1 см изображено кольцо. Найдите его площадь. В ответ запишите площадь, делённую на
Ответ дайте в квадратных сантиметрах.
6
На клетчатой бумаге с размером клетки 1 см 1 см изображено кольцо. Найдите его площадь. В ответ запишите площадь, делённую на
Ответ дайте в квадратных сантиметрах.
7
На клетчатой бумаге с размером клетки 1 см 1 см изображено кольцо. Найдите его площадь. В ответ запишите площадь, делённую на
Ответ дайте в квадратных сантиметрах.
8
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
9
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
10
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
11
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
12
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
13
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
14
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
15
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
16
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
17
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
18
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
19
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
20
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
21
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
22
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
23
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
24
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
25
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
26
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
27
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
28
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
29
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
30
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
31
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
32
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
33
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
3 октября 2013
Сегодня мы разберем нестандартную задачу B5 на площади из ЕГЭ по математике. В этой задаче требуется найти площадь закрашенного кольца, которое представляет собой две концентрические окружности разных радиусов:
Задача. Найдите площадь S закрашенного кольца, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S/π.

Как и во всех задачах, для решения нам потребуется формула площади круга:
S = πR2
где R — радиус круга. Это стандартная формула, и ее обязательно надо знать. Но поскольку в задаче фигурируют два круга, то и радиусов будет два. Обозначим внутренний радиус (меньшей окружности) буквой R1, а внешний радиус — R2. Внутренний радиус очень легко считается, он равен двум клеточкам:
R1 = 2 ⇒ R12 = 4
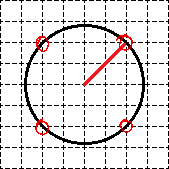
Со вторым радиусом все сложнее. Окружность не проходит через «классические» точки горизонтальной и вертикальной осей, по которым обычно измеряется радиус. Однако на этой окружности есть другие точки, которые лежат в узлах исходной сетки. Отметим эти точки красным:
Что дают нам эти точки? Как минимум — визуальное представление того, как выглядит радиус. Для того, чтобы его вычислить, давайте отдельную сетку, на которой отметим центр окружности O и ту точку A на нашей окружности, в которую мы провели радиус. Затем достроим полученный отрезок до прямоугольного треугольника, двигаясь вдоль линий сетки. Получим треугольник OAC с прямым углом C:
По теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов) получаем:
R2 = OA2 = OC2 + AC2 = 22 + 22 = 4 + 4 = 8
Итого мы получили:
R22 = 8
Теперь осталось найти площади внешнего и внутреннего кругов, образующих кольцо:
S1 = πR12 = π · 4 = 4π;
S2 = πR22 = π · 8 = 8π.
Поскольку закрашенное кольцо лежит между границами кругов, для нахождения его площади надо из площади большего круга S2 вычесть площадь меньшего круга S1. Получаем:
S = S2 − S1 = 8π − 4π = 4π
Но это еще не ответ! В задаче требуется найти величину S/π. Давайте сосчитаем:
S/π = 4π/π = 4
Вот мы и получили ответ! Как видите, ничего сверхъестественного в этой задаче нет. Достаточно помнить формулу площади круга, а также находить эту площадь через радиус, даже если этот радиус приходится считать через теорему Пифагора.
Надеюсь, этот урок сильно поможет тем, кто всерьез готовится к ЕГЭ по математике. Тем, кто не рассчитывает на то, что им попадутся легкие задачи (в частности, задача B5), а готовится решать в том числе и нестандартные примеры. В общем тренируйтесь — и обязательно сдадите экзамен на отличный балл.:)
Смотрите также:
- Нестандартная задача B5 на площадь круга
- Задача B5: площадь закрашенного сектора
- Десятичные дроби
- Специфика работы с логарифмами в задаче B15
- Семинар: ЕГЭ по математике, задачи B3 на площади
- Решение задач на движение по воде
Решение:
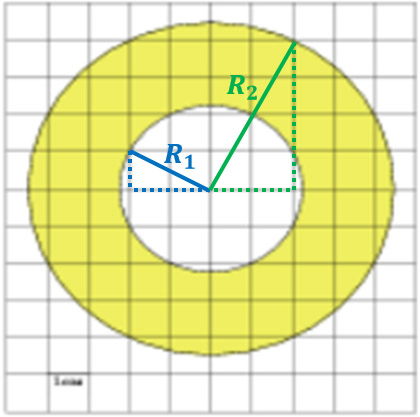
Окружности нарисованы не очень удачно потому, что мы не можем с точностью сказать, какова длина у их радиусов. Придется искать.
Начертим радиусы этих двух окружностей так, как показано на рисунке, а затем сделаем еще одно дополнительное построение: достроим эти радиусы до прямоугольных треугольников.
Теперь с помощью теоремы Пифагора можно найти длины радиусов.
Далее найдем площадь маленького круга с радиусом R1 и большого круга с радиусом R2.
Чтобы найти площадь кольца надо из площади большого круга вычесть площадь маленького:
В ответе нас просят записать площадь, деленную на π, т.е. просто 15.
Ответ: 15.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
#799
Решение:
Площадь кольца это разность между площадью большого кольца и площадью маленького кольца.
Площадь круга находится по формуле S⚫= πR2.
Радиус маленького круга R1 = 2 см, найдём его площадь:
S1⚫ = πR12 = π·22 = 4π см2
Радиус большого круга найдём по теореме Пифагора из прямоугольного треугольника:
R_{2}=sqrt{1^{2}+2^{2}}=sqrt{5}
Площадь большого круга равна:
S2⚫ = πR22 = π·(√5)2 = 5π см2
Площадь кольца равна:
S = S2⚫ – S1⚫ = 5π – 4π = π см2
В ответе укажем frac{S}{pi}:
frac{S}{pi}=frac{pi}{pi}=1
Ответ: 1.
Skip to content
ЕГЭ Профиль №1. Окружность, касательная, хорда, секущая
ЕГЭ Профиль №1. Окружность, касательная, хорда, секущаяadmin2022-08-28T09:29:12+03:00
Скачать файл в формате pdf.
ЕГЭ Профиль №1. Окружность, касательная, хорда, секущая
| Задача 1. Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны (frac{4}{{sqrt pi }}) и (frac{2}{{sqrt pi }}).
Ответ ОТВЕТ: 12. |
 |
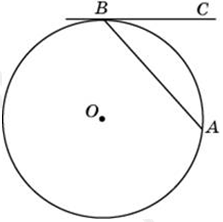
| Задача 2. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
Ответ ОТВЕТ: 46. |
 |
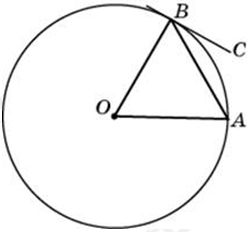
| Задача 3. Угол между хордой AB и касательной BC к окружности равен 32°. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.
Ответ ОТВЕТ: 64. |
 |
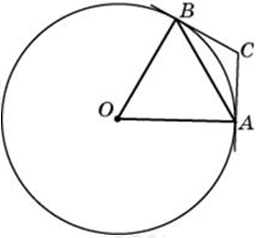
| Задача 4. Через концы A, B дуги окружности в 62° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.
Ответ ОТВЕТ: 118. |
 |
| Задача 5. Касательные CA и CB к окружности образуют угол ACB, равный 122°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
Ответ ОТВЕТ: 58. |
 |
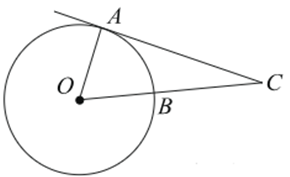
| Задача 6. Найдите угол ACO, если его сторона CA касается окружности, О — центр окружности, сторона CO пересекает окружность в точке B, а дуга AB окружности, заключенная внутри этого угла равна 64°. Ответ дайте в градусах.
Ответ ОТВЕТ: 26. |
 |
| Задача 7. Угол ACO равен 28°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.
Ответ ОТВЕТ: 62. |
 |
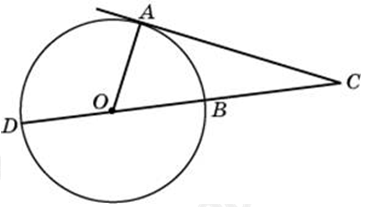
| Задача 8. Найдите угол ACO, если его сторона CA касается окружности, O— центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.
Ответ ОТВЕТ: 26. |
 |
| Задача 9. Угол ACO равен 24°. Его сторона CA касается окружности с центром в точке O. Найдите градусную меру дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.
Ответ ОТВЕТ: 114. |
 |
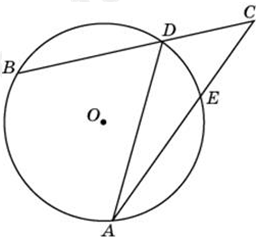
| Задача 10. Найдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные меры которых равны соответственно 118° и 38°. Ответ дайте в градусах.
Ответ ОТВЕТ: 40. |
 |
| Задача 11. Угол ACB равен 42°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах.
Ответ ОТВЕТ: 20. |
 |
- Главная→
- Видеоуроки→
- Вычисление площади кольца
Вычисление площади кольца
В данном уроке рассматривается пример решения задачи на определение площади кольца. Уроком рекомендуется воспользоваться при подготовке к ЕГЭ по математике.
Найдите площадь S кольца, считая стороны квадратных клеток равными 1. В ответе укажите S/π.
Интересная статья? Поделитесь ей с другими:
Лучшие цены на образовательные товары. На сайте дешевле, чем в магазинах.
Нажимая на кнопку, вы даете согласие на обработку своих персональных данных и соглашаетесь с Условиями использования.
Горячая линия
8 (800) 100-52-31
28
Авг 2013
Категория: 01 ГеометрияПланиметрия
01. Круг
2013-08-28
2022-09-11
Видео к теме 1; 2; 3; 4
Задача 1. Найдите площадь круга, длина окружности которого равна
Решение: + показать
Задача 2. Площадь круга равна . Найдите длину его окружности.
Решение: + показать
Задача 3. Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны и
Решение: + показать
Задача 4. На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 4. Найдите площадь заштрихованной фигуры. Видеорешение*
Решение: + показать
Задача 5. На клетчатой бумаге с клетками размером 1 см x 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. В ответе запишите . Видео*
Решение: + показать
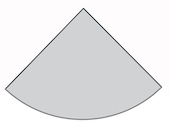
Задача 6. Найдите площадь сектора круга радиуса 6, длина дуги которого равна 3.
Решение: + показать
Задача 7. Площадь сектора круга радиуса 3 равна 15. Найдите длину его дуги.
Решение: + показать
Задача 8. Найдите центральный угол сектора круга радиуса , площадь которого равна 96. Ответ дайте в градусах.
Решение: + показать
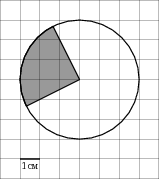
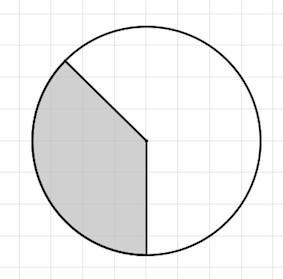
Задача 9. На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 56?
Решение: + показать
Задача 10. На клетчатой бумаге с клетками размером 1 см x 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. В ответе запишите . Видео
Решение: + показать
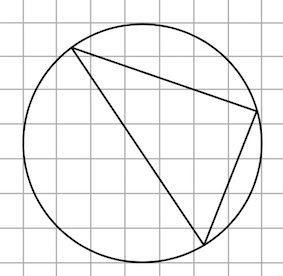
Задача 11. На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите радиус описанной около него окружности.
Решение: + показать
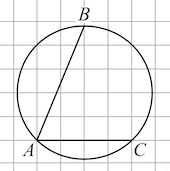
Задача 12. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC Ответ дайте в градусах.
Решение: + показать
Вы можете пройти тест
Автор: egeMax |
комментариев 14